基于协作机器人关节集成扭矩传感器的研究

朱弟发，张恩阳，韩 康，徐振邦，王忠素

(1.中国科学院长春光学精密机械与物理研究所，吉林长春 130033；2.中国科学院大学，北京 100049)

0 引言

协作机器人作为新兴产业代表[1]，被视为实现中国制造2025的关键[2-3]。协作机器人由于与人协同工作更强调安全性[4]，高灵敏的扭矩传感器能够准确测量机器人关节受力情况，从而确保足够的安全性。而如何获得最优的传感器弹性体结构一直是设计难题[5]。潘新安等通过将应变片粘贴在谐波减速器柔轮上测量扭矩，但是柔轮的噪声对测量影响很大[6]；文献[7]设计了“弹簧离合器”式传感器，能减少关节的碰撞力；文献[8]设计了一款异形体传感器，灵敏度高但弹性体结构复杂难以加工；王罗罗等设计一款带有保护梁的扭矩传感器，测量应变梁的剪切应变，应变较小[9]；蒋聪等对轮辐式结构进行了优化设计，加工性好但增加了关节轴向尺寸[10]。

本文在详细分析传统关节扭矩传感器测量原理的基础上，基于一体化设计理念，提出了扭矩传感器与输出轴一体化结构，降低了关节轴向尺寸，提高了关节负载/自重比。同时，借助有限元仿真及响应面法，得到了一种扭矩传感器弹性体的优化方法。

1 扭矩传感器需求分析及结构设计

1.1 传感器需求分析

图1为新一代协作机器人的关节内部结构，即本文传感器设计的应用对象。由于关节外壳、谐波减速器已确定，故传感器最大外径应小于关节上壳内径(63.5 mm)，内轮缘上螺栓圆中心线直径为27 mm，最大高度12 mm。根据机械臂工况需求，扭矩传感器量程为0～30 N·m，且具有2.5倍的抗过载能力，即传感器能承受75 N·m的瞬时载荷，载荷释放后，传感器仍可正常工作。

1.2 传感器整体设计

为最大程度减小关节尺寸，降低关节整体质量，采用一体化设计理念，将关节输出轴与传感器设计为一体，整体安装示意图如图2所示。

扭矩传感器的内轮缘与谐波减速器的输出端柔轮通过谐波压圈螺栓连接，扭矩传感器的外轮缘与轴承基座连接，传感器的末端与绝对值编码器转子连接，便于对关节进行位置控制；同时，采用交叉滚子轴承进行支撑，有效避免轴向力与径向力对扭矩传感器的干扰，提高传感器测量的准确性与可靠性；最后通过输出转接件将运动传递至下一关节。

1.3 传感器弹性体设计

考虑到机械臂关节负载较小，内部空间有限，故采用4条轮辐的弹性体结构，一方面便于后期加工和应变片粘贴，另一方面利用其剩余空间便于后期调理电路板的安装。轴承基座和扭矩传感器结构如图3、图4所示。

传感器弹性体通常要求材料屈服极限高、耐腐蚀、各向同性及加工性好，在对比常用材料后，选择铝合金7075-T6，其材料特性如表1所示。

表1 7075-T6特性表

2 传感器力学模型分析

建立传感器弹性体力学模型，分析弹性体所受力与应变梁变形之间的关系，方便进一步优化传感器结构。由于传感器过渡轴段部分几乎不受力，所以受力分析时可忽略。传感器弹性体的变形主要是应变梁的弯曲变形，加载环与固定环的变形可近似忽略，弹性体可简化为如图5所示。图5中，固定环最大外径为R2，加载环外径为R1，应变梁长度为l，宽度为h，厚度为b。

传感器只受到扭矩M的作用，取加载环为受力研究对象。加载环受到两部分作用力：扭矩M和应变梁的反作用力；由弹性体对称结构可知4条应变梁的反作用力大小相同。取任一条应变梁与加载环接触点，建立力学模型，如图6所示。

应变梁的受力满足力平衡方程：

FR1+M1=M/4

(1)

应变梁的弯曲变形可分为2部分，作用力F引起的变形和扭矩M1引起的变形。

分析力F引起的变形，最大挠度yF与端面转角θF表示为：

(2)

分析扭矩M1引起的变形，最大挠度yM1与端面转角θM1表示为：

(3)

联立式(2)、式(3)求解，端面总转角θ为

(4)

端面总位移Δy为：

(5)

联立式(1)和式(5)求解得：

(6)

(7)

得到传感器弹性体在M作用下单条应变梁的应变为

(8)

式中：E为弹性模量；Wz为应变梁的抗弯系数，Wz=bh2/6。

3 传感器数学模型分析

传感器一项重要的性能评价指标为灵敏度，在正常使用情况下，传感器的灵敏度越高越好，传感器的灵敏度与弹性体的尺寸有重要关系。传感器灵敏度定义为

(9)

式中：ΔU为全桥输出电压；U为传感器激励电压；K1为应变片灵敏度系数；εT为真实应变。

灵敏度和真实应变成正比例关系，同时传感器弹性体需要满足强度校核，即σIV≤[σ]。

为了提高应变梁的应变集中效果，使测量结果更理想，在应变梁上开设腰型孔，如图7所示。

取应变梁厚度b及腰型孔位置尺寸L1、外形尺寸L2、D为优化变量，得到传感器弹性体优化数学模型为：

(10)

式中：f1(x)为应变片粘贴区域应变梁所受最大应力；f2(x)为应变片粘贴区域应变梁的真实平均应变；xmax、xmin为设计变量的上下限。

变量范围及目标值如下：

(11)

(12)

4 传感器仿真分析及优化

4.1 响应面法优化

本文对弹性体结构参数采用响应面法进行优化，采用多元二次回归方程来描述变量与响应值之间的对应关系。考虑到有4个变量因素，采用Box-Behnken法设计变量分组[11-12]，得到29组分组数据，借助UG/hypermesh对每组参数进行三维建模、受力仿真，得到每组应变梁最大应力及应变。得到应变梁最大应力及应变与变量的响应面曲线图，如图8、图9所示。

得到f1(x)、f2(x)拟合曲线如下：

f1(x)=428.83-49.08b+103.52D-30.70L1+

48.49L2-25.95bD-1.36bL1-14.05bL2+

3.07DL1+41.29DL2+10.30L1L2+13.08b2+

(13)

(14)

2组拟合曲线的拟合评估值如表2所示，p值均小于0.000 1，方差与调整方差相近，信噪比远大于4，说明曲线拟合可信度比较高。得到结构优化参数，如表3所示。

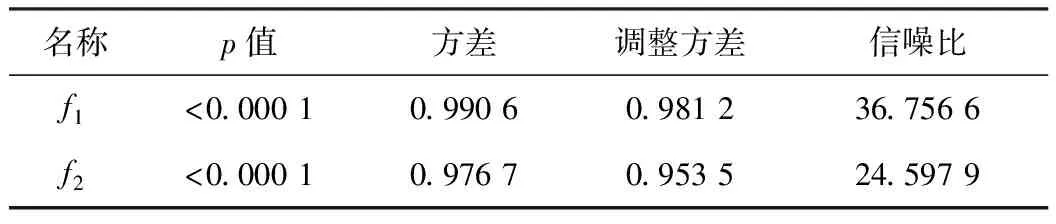
表2 拟合评估值

表3 优化参数 mm

将优化后的参数模型建模进行静力学仿真，弹性体应力云图如图10所示。得到传感器在2.5倍过载载荷75 N·m下，最大应力maxf1(x)=498.9 MPa<[σ]=503 MPa，最大应变maxf2(x)=6.243×10-3。可以看出传感器具有良好的抗过载能力。

4.2 模拟加载仿真

模拟传感器加载情况，得到应变片粘贴位置应变梁的平均应变与负载的关系，如图11所示。得到应变与载荷的拟合曲线：

y=71.78x+1.71

(15)

式中：y为应变；x为载荷。

得出拟合线性度误差0.75%，满量程30 N·m时粘贴区域平均应变为2 159×10-6。

5 结束语

本文基于一体化设计理念，利用输出轴设计了一款针对新型协作机器人关节的扭矩传感器，未增加关节尺寸。对传感器弹性体建立了力学模型、数学优化模型、三维仿真模型，利用响应面法对传感器结构参数进行了优化，从而提高传感器的灵敏度，确保足够的安全性。结果验证，优化效果可靠性比较高，传感器拟合线性度误差0.75%，满量程时粘贴区域平均应变为2 159×10-6，安全裕度2.5。同时，本文所采用的分析与优化方法也适用于其他尺寸和类型的传感器。