谐振式微加速度计静电刚度应用分析及实验

刘 恒，舒进华，张 玉，杨添熠

(南京信息工程大学电子与信息工程学院，江苏南京 210044)

0 引言

微机械谐振式加速度计具有体积小、批量生产、功耗小、输出为频率信号抗干扰性强等特点[1-2]，其工作原理是通过加速度改变谐振梁有效刚度，从而改变谐振频率。主要有2种刚度改变类型：固有刚度改变型和外加静电负刚度型。固有刚度改变型中，加速度作用在可动质量块上产生惯性力，惯性力通过杠杆或直接加载在振梁的轴向端[1]。惯性力直接加载方式灵敏度小，接口电路难满足高分辨率的加速度敏感要求；杠杆力放大方式虽能提高灵敏度，但杠杆重复性差，容易变形导致力放大系数发生偏离或杠杆失效无法实现力的转换。微机械谐振式加速度计谐振频率与谐振梁的模态等效刚度和质量有关，一旦微结构流片后谐振频率就确定了，由于制造工艺误差的存在，微机械加速度计的谐振频率与设计期望值存在一定的偏差，基于机械固有刚度改变型无法实现灵敏度等参数的后续调整。基于平板电容的静电负刚度谐振加速度计能够在流片后利用加载电压来调节指标参数[3-5]，通过加速度改变电容平板间距，间距又影响静电负刚度，静电负刚度与检测电压和加速度大小有关，静电负刚度和机械刚度又决定谐振频率[5]，整个原理过程存在非线性，难以精确求解出灵敏度；同时静电负刚度的存在，需要微结构中存在平板电容，加速度作用在平板电容上会引起质量块与谐振梁发生吸合现象[6]，限制了量程。文中介绍了静电负刚度谐振式加速度计的原理，并在约束条件下推导得到灵敏度及临界检测电压表达式，设计并制造了加速度计和开环测控电路，实验测试对理论推导进行了验证，为版图优化设计和闭环电路调试提供了实验基础。

1 微机械谐振加速度计原理

基于静电刚度的微机械谐振式加速度计结构如图1所示，为上下对称结构，由2个音叉梁构成差分结构。每个音叉梁形成1个谐振子系统，包括谐振梁、固定的驱动梳齿、检测平板电容系统。检测平板电容系统包括4个折叠梁，每个折叠梁通过锚点连接悬空，敏感质量块通过折叠梁支撑悬空，为减少阻尼，质量块上有开孔，质量块一侧有电容平板。作为谐振子，谐振梁上的梳齿与固定驱动梳齿构成驱动电容，1个谐振子有2组驱动电容，2组驱动电容通过电极连接在一起。

将差分式静电刚度谐振式微加速度计在中间对称处分为2个完全相同的单梁谐振加速度计，单梁结构见图2。

检测平板电容系统连接直流检测电压Vs，方波通过隔直电容后为Vm，且与谐振音叉梁连接，固定驱动梳齿接直流偏置电压Vd和交流电压Vcsinωt，Va=Vd+Vcsinωt。对于隔直后高频对称方波电压Vm，其频率远大于振梁谐振频率，等效为接地(平均值为0)。谐振梁的动力学方程为

(1)

式中：x为音叉梁振动的模态位移；Fd为静电驱动力；k为音叉梁振动模态的有效机械刚度；m为振动模态的等效质量；C为阻尼系数；Fe为检测平板电容作用在谐振梁的静电力。

检测平板总电容Cs为

(2)

式中：N为平行板电容的对数；g0为单个检测电容与谐振子的Y方向初始间距；ε为介电常数；h为电容极板沿Z方向的交叠厚度；l为沿Y方向单个电容正对极板的长度；A为检测平板电容等效正对面积，A=Nhl。

静电力Fe为

(3)

驱动梳齿结构的总电容Cd为

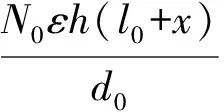
(4)

式中：N0为驱动梳齿电容的对数；l0为单个梳齿的交叠长度，沿Y方向；d0为梳齿对X方向的间距。

静电驱动力Fd为

(5)

式中Va为梳齿电容的驱动电压。

将式(3)、式(5)代入式(1)中，忽略静电力的高次项，有：

(6)

谐振梁的等效刚度Keff为

(7)

式中ke为加速度为0时的静电刚度。

在加载直流电压Vs时，谐振梁的等效刚度减小，对应的谐振频率减小，减小量与Vs和g0有关。建立Y轴方向加速度a与g0的映射关系就可构建谐振式加速度计。

根据图2可知，加速度计结构中检测平板电容系统和谐振梁在Y方向加速度作用下均会发生移动，间距g0的求解较复杂。在设计中，约束检测平板电容系统中折叠梁在Y方向的等效刚度ks远小于谐振梁模态刚度k，同时检测质量块质量ms远大于谐振梁m质量。在静电驱动力作用下，谐振梁关于固定平衡位置做高频正弦周期性振动，等效低频位移为0。

在Y轴方向加速度a=0时，对于检测平板电容系统有：

(8)

在Y轴方向加速度a≠0时，对于检测平板电容系统有：

(9)

式(8)和式(9)中，x和Δx分别为加速度a=0和a≠0时，折叠梁和质量块在Y方向的位移。在实际设计中，应考虑平板电容器的下拉效应，即尽量增大g0的值，但太大也将带来输出信号的检测困难，一般满足：x-Δx<

(10)

谐振梁谐振频率fe在静电负刚度作用下为

(11)

对式(11)近似化简，有：

(12)

式中：β为a≠0的静电刚度和机械刚度比；f0为谐振梁固有模态频率；α为a≠0时谐振梁动态位移和静态位移比。

则有：

式中Ke′为a≠0时的静电刚度。

灵敏度S表示为

(13)

式(13)整理后有：

(14)

根据式(14)，在刚度比及质量比约束下，灵敏度与敏感质量块的质量ms成正比，大的质量块能提高灵敏度；同时与工作模态的结构固有刚度和质量有关，减小谐振梁固有机械刚度k和谐振梁质量m均可提高灵敏度，但并不表明大的结构固有谐振频率f0意味大的灵敏度。大的静电刚度ke对应大的灵敏度，意味间距g0越小灵敏度越大，同样直流检测电压Vs越大，灵敏度越大，但太大的直流检测电压Vs会发生平板电容的吸合，导致微结构失效。

中国—东盟博览会永久落户南宁，不仅为南宁吸引了大量的外部投资，也为南宁的旅游业带来了充足的客源。因此，中国—东盟博览会在推动南宁经济的同时，也使南宁旅游业整体质量的提高。东博会和旅游业的良性互动，使得两者融合发展，促进南宁城市竞争力。在中国—东盟博览会的影响下，南宁的旅游业不断向好向快发展；而南宁旅游业的完善也在一定程度上保证了东博会举办的质量。两者的互动迎来社会和谐发展共赢的局面。

对于式(14)，灵敏度S>0，有：

(15)

检测平板电容系统质量块在惯性力作用下产生位移，根据能量守恒定律有[7]：

(16)

求解后得到临界检测电压Vsp：

(17)

对于0

(18)

由式(18)可知，在加速度a≠0时，a越大，则对应的临界检测电压越小，即允许加载的检测电压越小。相同条件下，结构振动位移越接近临界位移，结构稳定性变差，这就限制了加速度计的量程。对于灵敏度来说，根据式(14)可知，检测电压越大，灵敏度越大。量程与灵敏度相互制约，在检测电压大小的选择上要折中考虑。

2 加速度计制造及测试

(2)扩散掺杂浓硼，增加结构的导电性；

(3)在硼硅玻璃上溅射金然后光刻出电极和引线；

(4)将玻璃和硅用阳极键合技术进行键合；

(5)将键合后的硅片背面用干法刻蚀多余硅，将结构层减薄；

(6)硅片背面用深硅刻蚀工艺刻蚀出微结构。工艺流程方法成品率高，结构与衬底间的间隙容易控制，污染杂质少，只需3块掩模版，3次光刻，工艺流程相对简单，成本低。工艺流程见图3。

在刻蚀深度为30 μm条件下，第1版双级和单级折叠梁流片后如图4、图5所示，焊接金属引线后，折叠梁局部放大后见图6，单级和多级折叠梁流片均未发生折叠梁变形。第1版2种设计版图中的电极连接均存在8个电极，开环测试表明电极之间存在较大的交叉寄生电容。同样工艺流程下，改进了单级折叠梁微加速度计的电极层设计，将原来的8个电极减少到5个，上下2个音叉梁均只配有1个检测电极、1个驱动电极和1个公共音叉电极。上下2个音叉梁对应的电极相互分开布局，减少极板间耦合电容，第二版流片电镜放大表芯见图7，没有折叠梁和谐振梁的变形。

利用计算机视觉方法对微结构几何尺寸进行测量，如图6、图7的尺寸标注线，得到表1～表4的测量尺寸。根据测量尺寸计算得到微结构刚度、质量等参数，代入式(14)，得到单个谐振梁输出频率与检测电压在水平放置(0g)、敏感轴正向(1g)、敏感轴反向(-1g)的曲线，如图8所示，加速度计在检测电压较小时，加速度变化带来频率变化较小，灵敏度小；增大检测电压，在正向加速度激励下，频率变化大，反向频率变化小，这与间距非线性变化及频率与刚度非线性有关，正向加速度和反向加速度激励频率变化曲线不对称；在加速度和检测电压增大时，反向间距增大，静电刚度减小，谐振频率相对变大。

μm

表2 折叠梁、音叉梁及折叠梁连接端测量尺寸 μm

表3 平板电容及连接梁测量尺寸 μm

表4 阻尼孔、质量块测量尺寸 μm

由于微结构在常压封装下振动幅度小，对表芯结构进行金属管壳真空封装，减少谐振能耗，对第1版和第2版均采用同样的封装，封装的加速度计见图9。由于检测电容端存在驱动交流信号直接耦合到检测端，开环测控电路采用方波调制和开关解调的方法来消除同频干扰问题，见图10，测控电路外接直流驱动电压，交流驱动电压信号由Agilent35670A提供。解调和滤波后的检测信号输入到Agilent35670A，扫频范围为34～40 kHz，通过直流稳压电源来调整检测电压，获得幅频曲线。

图11和图12为检测电压Vs依次为2.5、5、6、6.5 V的静态测试条件(敏感轴方向加速度为0)下，一个音叉梁的幅频曲线的谐振频率依次为37.136、36.362、35.921、35.746 kHz，检测电压Vs增加，对应的谐振频率呈非线性的减小。在检测电压Vs改变过程中，幅频曲线并不左右对称[9]，但4种情况下均没有出现幅值的大幅度跳变，表现在4个图曲线的纵轴方向值大小基本一致，排除幅度和频率的交叉耦合导致的频率变化[10]，应考虑为检测电压变化带来的静电负刚度效应。对3种情况下的加速度计进行开环测试，利用直流稳压电源调节检测电压大小，电压间隔为0.5 V，变化范围为0.5～8 V，得到图13所示的单梁检测电压与谐振频率的曲线，测试表明：输出频率随检测电压的增大而非线性减小，大的检测电压意味大的灵敏度。当存在工艺误差时，通过加载不同大小检测电压来调整灵敏度，但测试与理论计算存在一定偏差，变化趋势一致。

在倒置1g加载加速度下，检测电压加载到30 V时，保持直流驱动电压为24 V，交流驱动电压幅值为2 V，观察到幅频曲线在重复多次扫频实验中不一致[11-13]。打开金属管壳封装，利用显微镜观察到平板电容检测系统中的折叠梁在大的检测电压下发生形变，见图14，局部放大观察到折叠梁不再如图4一样规则，双级折叠梁在上下方向上存在梁的变形，见图15，实验表明在大的检测电压和加载加速度激励下，加速度计会发生不稳定及失效，考虑到流片的成功率及实验条件，前期工作没有做进一步极限实验。

3 结束语

可动平板电容加载直流电压会在极板间产生静电力，等效为平板的静电负刚度效应，利用静电负刚度设计微机械谐振式加速度计，推导了输出谐振频率在约束条件下的表达式，理论分析表明灵敏度和量程均可以利用直流检测电压来调整，但灵敏度和量程相互制约，在传感器设计中要折中考虑二者的满足。流片实验印证了理论分析，加速度计频率输出关于检测电压和加速度为非线性，大的检测电压和加载加速度会导致微结构稳定性变差和失效。