一种基于模态局域化的高性能MEMS静电压传感器
2021-11-06王子龙刘向明高雅浩彭思敏杨鹏飞毋正伟彭春荣
王子龙,刘向明,高雅浩,彭思敏,修 日,杨鹏飞,毋正伟,彭春荣,2
(1.中国科学院空天信息创新研究院传感技术国家重点实验室,北京 100190;2.中国科学院大学电子电气与通信工程学院,北京 100049;3.北京信息科技大学理学院,北京 100192)
0 引言
静电压传感器广泛应用于空间探测[1]、质谱分析[2]、静电监测等多个领域。目前常用静电压传感器主要包括接触式和非接触式,其中,接触式需要一个非常高的输入阻抗,对检测电路要求高。而非接触式一般包括3种工作原理,分别是:感应探针式、场磨式和反馈式。其中,感应探针式是基于电流积分式原理[3],通过改变目标与探针之间的距离进行读数,因此在每次读数之前都必须要进行校准,因此不适合连续读取表面电压。场磨式是通过机械马达带动屏蔽电极旋转,周期性地屏蔽感应电极,从而产生感应电流[4]。这种传感器精度较高,但由于需要马达驱动,易损坏,并且结构一般较大且复杂。反馈式由反馈回路和集成高压源构成,通过调节反馈回路实现被测面和传感器之间的电场等于零时,实现被测导体电压的探测。这种方式具有较高的精度,然而由于存在升压设备,存在高静电压触点等问题。因此研制一种高性能、低成本的静电压传感器具有重要的意义。对此,本文基于多自由度弱耦合谐振敏感结构的模态局域化效应,提出并研制了一种高性能微型静电压传感器。
1 MEMS静电压传感器设计与分析
1.1 工作原理
模态局域化的原理如图1所示,3个谐振器通过细长梁弱耦合连接,当无电压输入时,系统处于稳定状态,2个外侧的谐振器的振动幅度相同;当外电压输入时,其中上面的谐振器在静电力的作用下刚度降低,此时产生模态局域化现象,能量局限在该谐振器上,因此2个外侧谐振器的振动幅度比值相差较大。通过检测输出振幅比的大小,确定输出静电压的大小。相比于传统单自由度谐振传感器频率测量的方式,本文提出的三自由度弱耦合谐振结构测量振幅比的方式能够显著提高传感器的灵敏度2~3个数量级[5]。
1.2 结构设计与分析
静电压传感器的结构设计如图2所示,采用模态局域化原理,由3个对称排列的谐振器组成,谐振器1和谐振器3的机械刚度相同,相邻谐振器存在极小的间隙构成电容,当谐振器之间存在电压差时实现静电耦合[6],即在谐振器1、谐振器3上接地,谐振器2上施加耦合电压,即可实现弱耦合系统。当扰动电极上施加电压,在谐振器1上等效增加负的静电刚度扰动,因而系统结构失谐,产生模态局域化现象,使的谐振器1和谐振器3的振动幅度发生较大变化。通过检测电极测量外侧2个谐振器(3和1)的振幅比例变化,可以实现电压的检测。
结构中的调谐电极作用是在该电极上施加电压后,可以降低谐振器1或者谐振器3的刚度,进而用于解决初始刚度不对称,或者设置传感器的初始工作点,使传感器工作在线性范围内。
1.3 幅频特性分析
对于本文设计的静电压传感器可以等效为1个三自由度系统模型[7],如图3所示。
其中x1、x2、x3表示3个谐振器的位移,m1、m2、m3表示3个谐振器的质量,k1、k2、k3表示3个谐振器的机械刚度,kc表示谐振器之间的静电耦合刚度,Δk表示扰动电极对谐振器1造成的静电刚度扰动。传感器敏感结构有m1=m2=m3=m,k1=k3=1/3k2=k。当引入Δk,系统失谐产生模态局域化现象,对该模型建立微分方程,并求解可以得到谐振频率与刚度扰动Δk的关系,以及振幅比与刚度扰动的关系。
(1)
(2)
(3)
(4)
式中:ωip和ωop分别为系统同相模态和异相模态的频率,Hz;|x3/x1|ip和|x3/x1|op分别为系统同相模态和异相模态谐振器3和谐振器1的振幅比值。
β定义为
(5)
根据式(1)~式(4)得到该种原理的传感器的频率响应曲线和振幅比与刚度扰动的图,如图4和图5所示。考虑到传感器扰动刚度为正刚度时,同相模态的频率基本不变,异相模态频率变化较大,因此需要选取频率稳定的同相模态。选取同相模态时,振幅比与刚度扰动成正比,如图5所示。
由式(3)、式(4)可得,当|βΔk/k|>10,谐振器3、1振幅比与刚度变化近似为线性关系:
(6)
振幅比输出的灵敏度为
(7)
传统的单自由度的谐振式频率输出的灵敏度为[8]
(8)
根据式(7)、式(8)可知,基于振幅比的输出比基于频率的输出灵敏度高3~4个数量级[9]。
本文传感器结构中的静电压产生的刚度扰动为
(9)
式中:d为扰动电极和谐振器之间的间距,m;A为扰动电极和谐振器之间的正对面积,m2;ε为介电常数。
联立式(5)、式(6)、式(9),得出振幅比和输入静电压的关系为
(10)
由式(8)可以得到,振幅比的开方和输入电压为线性关系
(11)
所以,基于振幅比的三自由度输出灵敏度sAR_V为
(12)
式中:kc为谐振器之间的静电耦合刚度,N/m,k2为谐振器2的刚度,N/m;k为谐振器1和谐振器3的刚度,N/m。
对于耦合系数与施加的耦合电压关系为
(13)
式中:d1为谐振器1、3和谐振器2之间的间距,m;S为谐振器1、3和谐振器2之间的正对面积,m2。
2 制备工艺
器件采用SOI工艺制备,如图6所示。首先清洗SOI晶圆,然后用金属剥离工艺实现金属沉积。用光刻胶保护并用DRIE刻蚀顶层硅。晶圆正面覆盖保护材料并用DRIE刻蚀背面衬底。最后刻蚀埋氧层实现释放。实际制作出的器件SEM电镜图如图7所示。
3 测试平台搭建
为了实现传感器的性能测试,构建了传感器的真空测试系统平台,如图8所示。本文测试时保持真空度为2 Pa。直流耦合电压为40 V,直流驱动电压为4 V,交流驱动电压为200 mV。谐振器1、谐振器3的交流驱动扫频信号由信号源产生两路异相的驱动信号。
驱动器1和驱动器3输出的电流信号接入跨阻放大器异相端,跨阻放大器的同相端施加一个直流电压源,最终可将振幅变化转化为电压信号,然后再将该微弱信号放入仪表放大器中进行差分放大以消除馈通信号,最后再进入到锁相放大器中测得振动的幅度并进行除法运算。根据锁相放大器测出的数据得出不同的输入电压对谐振器振幅比的相对变化量,并绘制得出振幅比与输入电压的关系的曲线。
4 实验结果与分析
4.1 幅频特性
传感器谐振器1和谐振器3输出的幅频特性如图9所示。图9中频率较小的为同相模态,频率较大的为异相模态,不同大小的被测电压引起同相模态的频率变化比异相模态频率变化小。图10是施加被测电压后,传感器同相模态和异相模态频率的变化特性。可以看出,同相模态的频率变化斜率绝对值较小,而异相模态斜率绝对值较大。并依据图4可知,传感器工作在正刚度区域。这是由于器件本身存在工艺误差导致谐振器1比谐振器3的刚度大。因此产生正的刚度扰动ΔK。电压产生的刚度扰动由式(9)可以得出,刚度为负值,所以传感器本身固有的刚度扰动会随着电压的变大而逐渐降低。所以振幅比也会随着施加电压增大而降低。
而且由图9可知,随着被测静电压的增加,在同相模态时,谐振器1振幅增大,谐振器3振幅缓慢增大,谐振器3与谐振器1的振幅比在降低;在异相模态时,谐振器1振幅降低,谐振器3振幅增大。
测试结果与理论上一致,也验证了传感器敏感结构产生了模态局域化效应。
4.2 灵敏度特性分析
为了实现静电压测量,由于传感器工作在正刚度区域,对此考虑了以下3种情况。
4.2.1 检测异相模态时频率输出
测试结果如图11所示,f0选取为图10中27 V测试的频率,计算拟合得出基于异相模态频率输出的灵敏度为
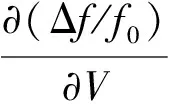
(14)
4.2.2 检测同相模态时的谐振器振幅比输出
选取同相模态的谐振器1和谐振器3的振动幅度,对其进行数据处理,得到图12所示的响应图。其中在该范围内具有较好的线性,线性相关系数为0.984 1,线性度6.11%。
基于同相模态振幅比输出的灵敏度为
(15)
4.2.3 检测异相模态时的谐振器振幅比输出
选取异相模态的谐振器1和谐振器3的振动幅度,对其进行数据处理,得到图13所示的响应图。其中在该范围内的灵敏度为0.050 7,且拟合的R2值为0.899 8。线性度差。
根据式(14)和式(15),可以得到基于振幅比的输出是基于频率输出的87.9倍。且选取同相模态输出具有较好的线性度。
5 结束语
基于SOI工艺,研制出一种基于模态局域化效应的三自由度硅微机械谐振式高性能MEMS静电压传感器。该传感器线性度为6.11%,能实现高灵敏度静电压测量。
