光纤光栅液位传感器设计及其灵敏度分析
2021-11-06杨才千唐人杰
杨才千,唐人杰,文 峰,杨 宁,李 帅,周 正
(1.东南大学土木工程学院,江苏南京 210096;2.湘潭大学土木工程与力学学院,湖南湘潭 411105;3.山东航天电子技术研究所,山东烟台 264670)
0 引言
液位监测是过程控制中的重要参数,在工业生产及日常生活得到了广泛应用。如探测石油化浆液面、化学储藏罐内的液体平面、监测汽油、柴油存储罐中的油位高度等。而在航空航天领域的液位测量中,由于其工作环境及测量精度的要求,对液位传感器不但要求精度高,而且要能承受恶劣环境的影响还能保持持续传感的能力,对安全性、强度及可靠度都有较高的要求。
布拉格光纤光栅(FBG)具有抗电磁干扰、抗辐射、抗腐蚀、耐高低温、不可燃,以及体积小、质量轻、柔韧性好等诸多优点,被广泛应用于传感领域,也受到了国内外诸多学者的关注和研究,测量方法不断在改进。殷小峰[1]等对弹性膜片进行封装,研制出了一种压力增敏FBG传感器。付华[2]等提出了一种自参照型POF耦合传感器,利用耦合比K可以识别所测液体,并区分气液体间的变化。赵呈锐[3]等提出了一种基于菲涅尔定律的光纤液位测量方法,利用介质折射率对双光纤光耦合效率的影响,可以实现对燃油的安全测量。张玉[4-5]等也对光纤液位传感器探头的光学特性进行了分离,论述了光纤传感探头和光源对传感器性能的影响,并分析了相应的光学和抗腐蚀特性。A. Kazemi[6]等提出了基于光纤长周期光栅(LPG)和基于全内反射(TIR)两种液位传感技术的光纤液位检测系统。然而,上述液位传感器均采用接触式方法对液位直接进行监测。对于部分处于腐蚀及极端条件下液体液位监测存在一定局限性。因此,本文提出一种非接触式液位传感器,避免介质对光纤传感器的耐久性损伤,能有效提高液位传感器的耐久性及适用范围。
本文基于浮力效应及杠杆原理,采用悬臂杠杆结构,通过调整沉管位置及直径实现液位传感器灵敏度与量程可调节,从而有效兼顾灵敏度及可探测液位量程。并提出了相应的理论模型及进行了试验验证。
1 传感器的设计及工作原理
1.1 基本原理
FBG是一种带阻滤波功能的无源光子器件,其带宽窄,波矢方向与纤轴方向一致,采用波长编码,结构如图1所示。FBG可以改变光的传播方向,当入射光通过光栅区域时,满足布拉格反射条件的光波会被反射回去,其他波长的光将透射,形成了反射和透射2种光谱,彼此互补。布拉格反射条件微分式为[7]:
(1)
当外界物理量(如温度、应力等)作用在FBG上并被它所感知时,会引起反射或透射光谱的波长漂移。通过对波长漂移的监测,即可测量和判断待测量的变化情况。
当光纤光栅受到应力及温度作用时,光栅的栅格周期常数在应力的拉伸作用下和热涨效应将发生改变;同时,光纤光栅中发生的弹光效应和热光效应将改变其折射率,即:
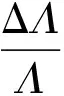
(2)
(3)
式中:ε为轴向应变;P11和P22为弹光系数;υ为泊松比;α为光纤材料的热膨胀系数;V为光纤的归一化频率。
把式(2)和式(3)及Pe、ξ代入式(1),可得应变作用的表达式:
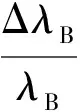
(4)
FBG液位传感器主要是利用FBG对应变敏感的原理,通过波长的变化推出应变的变化,从而得到力的变化,最终换算出液面位置。由于FBG同时对温度和应变都敏感,因此在使用FBG时不可避免的会受到干扰。一般情况下实际得到的是温度和应变同时作用下的合漂移量[8]。
因此,若不采取任何措施的情况下,温度变化的影响对应变作用的采集是不可避免的,只有把温度变化引起的波长漂移量去掉,得到的结果才更加精确。本文采取补偿光栅法[9-10]及悬臂梁法[11]进行温度补偿,从而得到精确的液位测量。
1.2 传感器设计
本文设计的基于浮力定律的非接触式悬臂杠杆FBG液位传感器结构如图2所示。传感器包括保护外壳、基座、传力杆、沉管、悬臂杆以及2支串联的FBG。悬臂杆通过轴承铰接在基座上,传力杆连接在悬臂杆上,弹簧管封装保护FBG1并提供拉力拉住悬臂杆使其在控制范围内摆动,FBG1连接于悬臂杆与外壳之间。
当液位发生变化时,浮力随之改变,从而传力杆传到悬臂杆上的力发生改变,同时FBG的应力也随之变化,引起FBG1轴向应变,波长发生漂移。通过连接波长解调仪检测FBG1的中心波长,并进行标定,可以得到浮力的数据,从而推导出液位变化。FBG2不受力,不产生应变,用于温度补偿,也避免了应变与温度的交叉敏感。
1.3 灵敏度分析
本文设计的FBG液位传感器力学模型如图3所示。沉管和传力杆的重力与浮力的合力F1通过传力杆作用在悬臂杆上,并通过悬臂杆带动FBG1与弹簧管轴向拉伸,产生的合力记为F2。F1、F2时刻力矩平衡。计算关系式为
F1a=F2l
(5)
式中:a为传力杆与悬臂杆铰接点距悬臂杆与基座铰接点之间的距离;l为弹簧管与FBG1的轴线距悬臂杆与基座铰接点之间的距离。
由于对任意时刻F1变化的只有浮力,且因F1浮力的变化才导致F2的变化,F1和F2对铰接点的力矩平衡。由此即可得变化关系式:
ΔF浮a=ΔF2l
(6)
可把FBG1与弹簧管的组合部分看作一根弹簧,取等效弹性系数为K,即可得:
ρ液gAa·Δh=Kl·ΔlF
(7)
式中:A为沉管底面积;Δh为液位变化量;ΔlF为FBG1轴向伸长量。
不考虑温度影响时,FBG1中心波长的改变量与光纤轴向应变关系可以写为
Δλ=(1-Pe)λBε
(8)
FBG1的应变为
(9)
式中lF为FBG1的光栅长度。
从而可以得出波长变化量与液位变化量之间的关系:
(10)
将传感器灵敏度S定义为FBG中心波长改变量Δλ与液位变化量Δh之间的比值,即:
(11)
由式(10)可知:
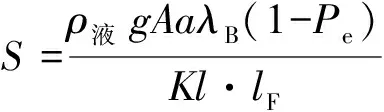
(12)
由式(12)可看出,影响灵敏度的因素主要有2个:沉管底面积A的大小,a与l的比值。且灵敏度S与A及a与l的比值成正比关系。
从力的关系上看,在同样的液位变化Δh下,灵敏度S取决于波长变化量Δλ的大小。由于Δλ取决于FBG1的拉伸变化量ΔlF,而FBG1的拉伸由F2引起,由ΔF1a=ΔF2l,F2的变化取决于F1的变化和a与l的比值。F1的变化也即是浮力的变化。在同样的液位变化Δh下,ΔF浮=ρ液gV排=ρ液gA·Δh,也即沉管底面积越大,浮力的变化也越大,因此F2的变化也越大,FBG1的拉伸量也越大。
从上述分析可知,灵敏度仅仅与a/l及沉管底面积A的大小有关。
2 实验与分析
为了验证上述关系,同时表征传感器对液位的响应特性,制作了传感器原型,在实验室条件下进行测试,原理图如图4所示。实验仪器包括Si255光纤解调仪、测试桶、刻度尺。
连接液位传感器、解调仪及计算机等实验装置,将液位传感器安装到测试桶内,刻度尺紧贴测试桶壁且竖直固定放置,测试时缓慢往桶内加水,待液面平静后记录数据。液位每上升1 cm记录一次,液位测量范围为2~30 cm。为了避免偶然误差,以下实验均做了3组重复性实验。
2.1 不同悬臂位置对灵敏度的影响实验
实验选取了悬臂杆1/2位置和杆端位置,验证不同悬臂位置对灵敏度的影响。图5为不同悬臂位置中心波长与液位拟合后的曲线,每隔5 cm取一个点。由图5可知,在1/2位置处中心波长与液位之间的线性度为0.997,灵敏度为7.47 pm/cm;在杆端位置处中心波长与液位之间的线性度为0.999,灵敏度为15.52 pm/cm。
图6为不同悬臂位置各个液位的灵敏度曲线。由图6可知,杆端位置的灵敏度明显大于在1/2位置处,且大致呈2倍关系。
由以上实验可知,采用上述设计的结构封装方式,传感器中心波长与液位变化之间呈现很好的线性关系,线性度达到0.997以上。在悬臂杆不同位置连接光纤,灵敏度也不同,杆端位置的灵敏度为15.52 pm/cm,1/2位置处的灵敏度为7.47 pm/cm,杆端位置的灵敏度与1/2位置的灵敏度大致呈2倍关系,这也验证了灵敏度与不同悬臂位置的关系。
2.2 不同沉管底面积对灵敏度的影响实验
选取直径分别为40、60、100 mm的3根沉管进行实验,图7为不同沉管直径的传感器中心波长与液位之间的拟合曲线,每隔5 cm取1个点。由图7可知,40 mm沉管直径的传感器中心波长与液位之间的线性度为0.972,灵敏度为2.49 pm/cm;60 mm沉管直径的传感器中心波长与液位之间的线性度为0.993,灵敏度为5.49 pm/cm;100 mm沉管直径的传感器中心波长与液位之间的线性度为0.998,灵敏度为15.57 pm/cm。
图8为不同沉管直径的各个液位的灵敏度曲线。由图8可知,沉管直径越大,其灵敏度也越高。从测得的灵敏度数值上来看,灵敏度与沉管直径的平方成正比关系。
由以上实验可知,采取不同直径的沉管来测液位,传感器中心波长与液位之间同样呈现很好的线性关系,线性度达0.97以上。沉管直径为40 mm时,线性度稍差一点。因为封装所用弹簧管刚度较强,因此,FBG对浮力变化响应较弱。
40、60、100 mm直径的沉管对应的灵敏度分别为2.49 pm/cm、5.49 pm/cm、15.57 pm/cm。灵敏度与沉管直径的平方成正比关系,即与沉管底面积成正比关系,验证了灵敏度与沉管底面积的关系。
3 结束语
首先,本文设计了一种灵敏度可调的光纤光栅液位传感器,并对其性能进行了表征,建立了光纤光栅中心波长与液位之间的对应关系。实验结果表明,该传感器对液位的灵敏度高,灵敏度可达15.57 pm/cm;对液面变化表现出高度线性响应,线性度可达0.999。其次,提出了影响灵敏度的2个主要影响因素,并进行实验验证。实验证明,灵敏度与悬臂位置及沉管底面积成正比关系。最后,值得强调的是,沉管材料可以使用任何材料,这也意味着本文设计的光纤光栅液位传感器可以应用于多种不同液体。同时,可使解调仪连接远程传输设备,实现远程实时液位监控。
