逐步Ⅱ型删失数据下广义指数分布形状参数估计*

林玉婷,韦程东,陈丽玲,罗文婷,唐璐薇,周昭君

(南宁师范大学 数学与统计学院,广西 南宁 530100)

1 引言

寿命试验是生存分析和可靠性分析中的基本工作之一，由于各种原因，试验通常会出现删失数据，而根据删失方式的不同，删失分为第一类删失、第二类删失和随机删失.广义指数分布是寿命试验研究中常用到的分布，是1999年Gupta和Kundu提出的一种重要分布，它可以有效地克服威布尔分布和伽马分布的不足[1]，在寿命试验研究中有较好的分析性，因此受到许多学者的关注.对于模型参数的研究，广大研究者使用极大似然估计法、贝叶斯估计法等等，统计推断中的贝叶斯方法依赖于先验分布和损失函数的选择.E-Bayes(期望贝叶斯)估计最早是由Han[2]提出的，是一种参数估计的新方法，该方法适用于样本小或可靠性高的删失数据.文[2]还讨论了一个真实数据，证明了E-Bayes方法的有效性.韩明[3]进一步讨论了E-Bayes估计的渐近性质.郭环[4]讨论了广义指数分布在定数截尾数据下的参数估计问题，给出了E-Bayes估计和多层贝叶斯估计的估计模型，运用蒙特卡洛算法得到了参数的数值解.韩明[5]讨论了在平方损失下，Poisson分布参数E-Bayes估计和多层Bayes估计的参数估计模型，并且研究它们的性质.接下来韩明[6]在前面工作的基础上，在不同损失函数下，推导出了Poisson分布参数的E-Bayes估计和E-MSE，用蒙特卡洛的方法模拟提出的估计方法，并且检验了它的性能.Han[7]讨论了指数分布未知参数E-Bayes估计和它的期望后验风险，并且在不同超参数先验分布下建立了E-Bayes估计模型和期望后验风险模型.Hassan Okasha[8]讨论了在自适应I型渐近混合删失数据下威布尔分布的E-Bayes估计，使用平方和LINEX损失函数得到了E-贝叶斯估计和相应的E-均方误差，研究了它们的性质.李东兵和胡文林[9]讨论了指数分布中参数为失效率λ的E-Bayes估计和多层Bayes估计的问题,并建立它们各自的模型，运用某型发动机的无失效储存数据，计算了参数的E-Bayes和多层Bayes的估计值，经过比较分析发现两种估计方法都是稳健的.许道军[10]在熵损失函数下，根据三种不同的超先验分布，给出了产品可靠度的E-Bayes估计模型和它的性质，并验证了结果可靠度的E-Bayes估计具有好的稳健性，说明得到的估计方法是可行的.本文在前人研究的基础上，对广义指数分布未知参数的E-Bayes估计进行了讨论，引入了E-Bayes估计的定义.在平方损失函数下，讨论了三种不同超先验分布对参数的E-Bayes估计的影响，通过R软件mcmc程序包进行数值模拟分析，检验我们广义指数分布形状参数的估计效果.

2 参数估计

2.1 模型描述

假设有N个寿命实验样本，ti为样本的失效时间，并设样本xi独立同分布且服从广义指数分布.第一个试验个体失效后，从剩下的N-1个试验个体中随机抽取R1个存活个体；第二个个体失效后，再从N-2-R1个试验个体中随机抽取R2个存活个体，如此下去，当第n个样本的失效时间ti在T在之前时，试验在xn点结束,这种删失模式为逐步Ⅱ型删失试验[11].

假设每个试验个体服从广义指数分布，其概率密度函数和累积分布函数如下：

f(x)=αλ(1-e-λx)α-1e-λx，

F(x)=(1-e-λx)α，

其中α和λ分别为形状参数和尺度参数，x≥0,α和λ≥0.

假设(X1∶N,X2∶N,…,Xn∶N)是逐步Ⅱ型删失样本，R=(R1,R2,…,Rn)是删失模式，尺度参数已知，则逐步Ⅱ型删失模式下试验个体的似然函数为

其中C=N(N-1-R1)…(N-n+1-R1-…-Rn-1).

2.2 基于逐步Ⅱ型删失数据的E-Bayes估计

假设试验个体都服从广义指数分布，并且α的先验分布是伽马分布，即α～Gamma(a,b)，则α的先验概率密度函数为

(1)

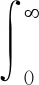
由贝叶斯定理，可得到α的后验密度函数，即

(2)

由式(2)可知，参数α的后验密度函数正比于似然函数与先验分布函数的乘积，所以我们可得

(3)

为了得到α的Bayes估计，首先引入一个引理.

引理1[8]在平方损失下，对于任何先验分布，α的Bayes估计为

选取α的先验分布为伽马分布，则先验分布密度函数为

(4)

由引理1我们可以得到α的Bayes估计如下.

定理1 在平方损失下，对于先验分布为伽马分布的广义指数形状参数α的Bayes估计为

证明由于α的先验分布如式(4)所示，所以由贝叶斯定理可得到α的后验分布为式(3)，因此由引理1可得α的Bayes估计为

由于以上积分比较复杂，不易求出，因此我们运用Lindley近似法得到α的Bayes估计.

近似计算法是Lindley提出来的[13]，它的形式如下：

其中θ=(θ1,…,θn)，l(θ)是似然函数的对数形式，u(θ)，g(θ)是θ的任意函数.

假设g(θ)是θ的先验密度函数，则u(θ)的后验均值为

其中ρ(θ)=lng(θ)，l(θ)+g(θ)是后验分布的对数形式.

对于广义指数两参数α未知，λ已知的情况，有

其中

我们将此应用到本文未知参数为α的估计式中，有ρ=lnπ(α)=(a-1)lnα-bα.

我们对对数似然中的α求二阶偏导可得

在平方损失函数下，u(α)=α,故后验期望为

由此定理得证.

为了得到未知参数的E-Bayes估计，我们引入一个定义.

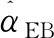
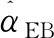
(6)

结合式(5)、(6)，我们给出α的三种E-Bayes估计.

定理2 在平方损失下，α的E-Bayes估计为

证明由定理1和定义1可得

由此定理得证.

3 数值模拟

采用MCMC算法进行数值模拟.首先给出产生广义指数分布下逐步II型删失数据的算法，这个算法是由Balakrishnan[16]在1999年提出来的.我们用R软件模拟生成数据，生成步骤如下：

(1)从均匀分布U(0,1)产生n个随机样本w1,w2,…,wn;

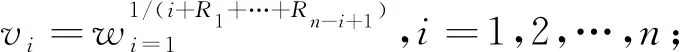
(3)让ui=(1-vnvn-1…vn-i-1),i=1,2,…,n；

我们给定α=0.5，λ=0.5，假设超参数a=0.5，b=0.25，用R软件中mcmc程序包里的metrop()函数进行贝叶斯估计的计算，在接受率为20%左右的情况下调整函数的各个参数，重复模拟10 000次，得到形状参数α的Bayes估计和E-Bayes估计并且得到它们的均方误差,下面的表1和表2给出了模拟的结果.

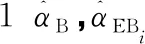
表和mse的计算结果(a=0.5,b=0.25,c=1,n=30,50,80,100)

表和mse的计算结果(a=0.5,b=0.25,c=0.5,n=30,50,80,100)

4 结论

本文在前人研究的基础上，基于逐步Ⅱ型删失数据讨论了广义指数形状参数的E-Bayes估计问题，引入E-Bayes估计的定义，在平方损失函数下建立了E-Bayes估计的定理，研究了三个超参数先验分布对E-Bayes估计的影响，通过数值模拟，比较了E-Bayes估计与Bayes估计的性能.模拟结果表明，得到的估计效果都比较稳健，E-Bayes估计在均方误差方面优于Bayes估计，在不同的先验分布下，估计的效果最好.本文的结果对于解决其他分布在逐步Ⅱ型删失数据下的参数估计问题具有参考意义.