参数未知系统的多模型对偶控制算法∗

杨恒占 高韵 付月园

（西安工业大学电子信息工程学院西安710021）

参数未知系统的多模型对偶控制算法∗

杨恒占 高韵 付月园

（西安工业大学电子信息工程学院西安710021）

论文针对参数未知的随机系统提出一种多模型对偶控制算法。首先使用多个子模型代替参数未知的系统模型，然后以传统的线性二次型高斯控制（LQG）为理论依据，引入后验概率，在多个模型中筛选出综合的参数模型，最后利用该模型对系统进行控制，获得一种新的多模型对偶控制策略。仿真结果表明了该文算法的有效性。

随机系统；对偶控制；多模型

Class NumberTP301.6

1 引言

不确定性无处不在。不确定性的存在使得在很多领域都不能用简单的模型进行分析，例如在实际工业生产、航天航空、经济等领域等，而必须采用随机理论方法进行控制。系统长期运行或运行于不同环境导致的参数变化，使得系统不仅会受到外界的随机噪声干扰（湿度、温度、风速等），而且系统模型参数本身也可能存在不确定性（零件的磨损程度、质量变化、压强等），即同时存在噪声的不确定性和模型参数的不确定性这两种不确定性［1］。

当系统模型中已知时，经典的随机理论现在可通过成熟的算法求出系统的最优解，但是经典控制理论的系统为简单的系统，即系统仅仅只有外部的噪声，当系统的模型未知时，经典理论不能求出最优解，因此，需寻求一种新算法对未知参数模型系统进行控制。从20世纪50年代开始，自适应控制问题已经开始进入研究者的视线，在其控制中，需要对两个方面需求进行满足：一是对被控对象的学习功能，即就是在控制的过程中累积有关对象特性的知识；二是控制功能，即在累积知识的同时对系统施加控制，使系统输出达到期望值［2～3］。

针对双重不确定性系统，传统自适应控制方法大致有两种思路：一是让均值取代未知参数，未知系统构造出一个已知系统，这种方法为确定性等价原理。但是此方法误差太大，且不能灵活地调节系统。二是首先对系统进行激励，收集系统运行信息，然后对收集的信息进行处理，辨识出未知参数，最后再依据辨识结果进行控制［4～7］。在这个过程中，一方面，信息收集过程对生产过程而言是一个消耗过程，本身不产生正向收益；另一方面，如果系统运行过程中参数发生变化，则控制效果必然会发生偏差甚至无法控制［8］。

对偶控制的出现，有效地解决了上述自适应控制存在的问题。对偶控制把对未知参数的辨识学习和对系统的目标跟踪综合一起，对系统边一边控制，一边辨识。即使系统运行过程汇总参数发生漂移或突变，也能够跟踪辨识参数变化并完成既定控制目标。相比传统的先辨识后控制的方法，对偶控制不仅具有闭环系统稳定性，而且对系统变化的参数可实时更新［9～10］。

本文针对一类参数未知的随机系统，将系统在不同情况下的系统结构和参数采用不同的辨识模型描述，以传统的线性二次型高斯控制（LQG）为理论基础，采用“简化分割，分而治之”的思想，根据每个子系统的模型分别设计各自的子控制器，以各子系统的后验概率为协调变量整合各子模型的控制率，对系统进行控制的同时进行模型辨识，设计出一种多模型对偶控制算法。

2 问题描述

参数模型未知且是多模型时，系统模型为

其中y(k)为m×1观测向量，x(k)是n×1状态向量，u(k)为r×1控制向量；{w(k)}，{v(k)}为模型噪声向量和量测噪声向量，且相互独立，均值都为0，协方差为高斯白噪声，分别为Q(k)和R(k)。θ为p×1向量，在参数空间Θθ内取值，可以认为参数未知且有多个模型。

状态转移阵Φ，增益阵G，量测阵H未知，在空间Θθ={Φi，Gi，Hi}，i=1，…，M内取值，由多个模型构成，模型的组数为M，θ在确定的或假定的先验概率密度函数p(θ)下是不确定的，系统参数真值是未知的。

控制目标是取得控制量{} u(0)，u(1)，…，u(N-1)，让性能指标为最小：

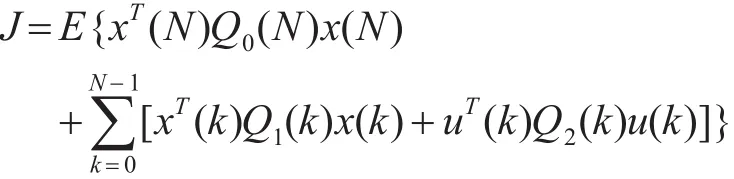
其中，Q0(N)，Q1(k)是半正定矩阵，Q2(k)是正定矩阵(k=0，1，…，N-1)。

3 控制器设计

当系统中参数包含未知的参数θ，即Φ，G，H参数未知的情况下，并且都由多个模型组成，因此要解决的问题为多模型参数未知的对偶问题。而经典的LQG问题中参数为已知，因此，在参数模型未知的情况下，原有的控制器不能继续使用。但是，从经典LQG问题求解的思路可以得到启示，通过在线计算和离线计算把各独立的函数乘积而得到的控制器，这种分离在对任意的闭环系统中都是可取的。因此，针对此问题，也可以对多模型进行设计：

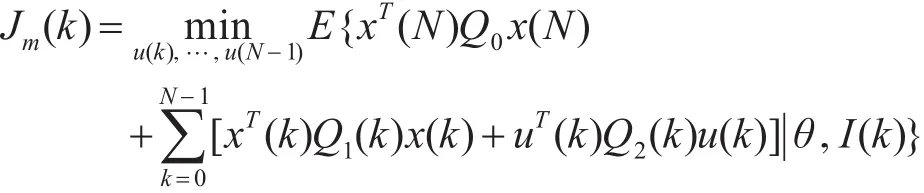
根据动态规划可知，其中Jm是一个在k每一次取值都会利用前一时刻的值计算得到的最优性能指标。

因此，根据动态规划性质可知：

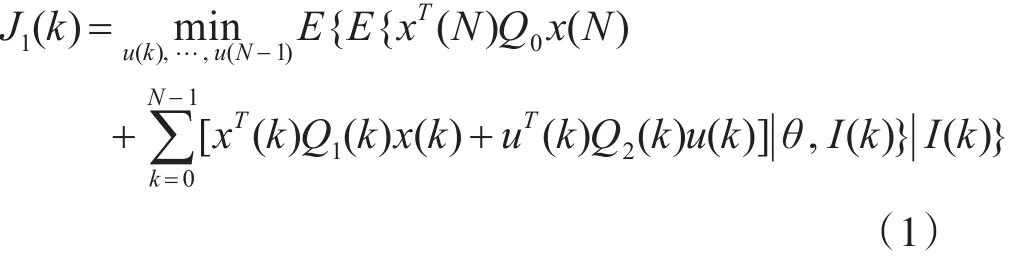
根据式（1）求出的u(k)为最优控制策略。但是由于维数灾问题，不能获得上式中的最小闭合解，因此，可对上式进行近似等价变型，可以最小化每一步的性能指标，从而求出一个问题次优解。因此，对式（1）进行近似，J1(k)的值可用下面的J2(k)给出，如下：

上式给出的J2(k)认为是一个加权平均值，当模型中的每一组参数为系统模型时，这时问题就成为经典的LQG问题，后验概率作为加权系数，具有以下特征：当参数模型为真实模型时，后验概率趋近于1，而当参数模型为非真实参数模型时，后验概率趋近于0。

后验概率是基本的信息理论，在实际中也有很多实例，在控制系统中，传感器接收到反馈的信息之后，测量端通过所了解到信息得出发送的概率就称为后验概率。后验概率在得到信息之后重新对概率进行修正，如贝叶斯公式中的反向推理问题，就是后验概率问题。而先验概率和后验概率有着密切的关系，先验概率可作为后验概率的基础［28］。

因此，对于多模型的加权控制问题，设计出多模型自适应控制系统框图如图1。

如图1所示，可以先通过动态规划离线计算状态增益矩阵K(k，θ)和滤波增益F(k，θ)，此过程是离线过程；然后针对每一个模型θ组成的系统，通过卡尔曼滤波预测出状态向量x(k|k，θ)和协方差矩阵，并通过LQG经典算法求出每一个模型的控制量u(k|k)，接着在根据后验概率P(k，θ)的公式求出每个模型的后验概率，最后，把每个模型的控制量乘以自己的后验概率，再通过加权的方式求出最终的控制器。在此过程中，离线的计算过程减小了在线计算的工作量，从而对运算速度有很大提高。

因此，针对参数未知的多模型自适应控制完整的算法流程给出如下步骤：

Step1：离线计算状态增益：

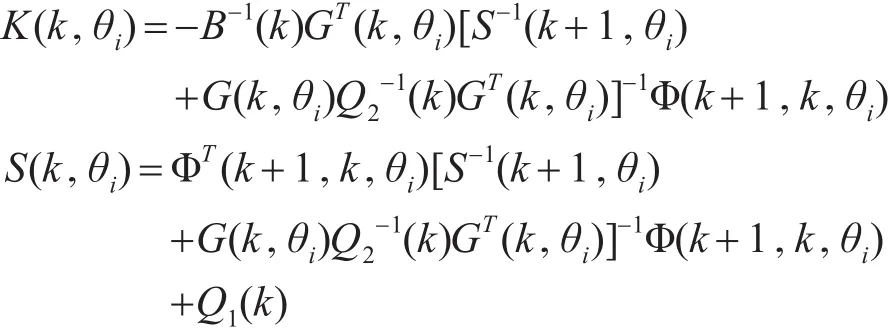
Step2：对第i个模型，利用Kalman滤波方法求解状态估计x(k/k，θi)：

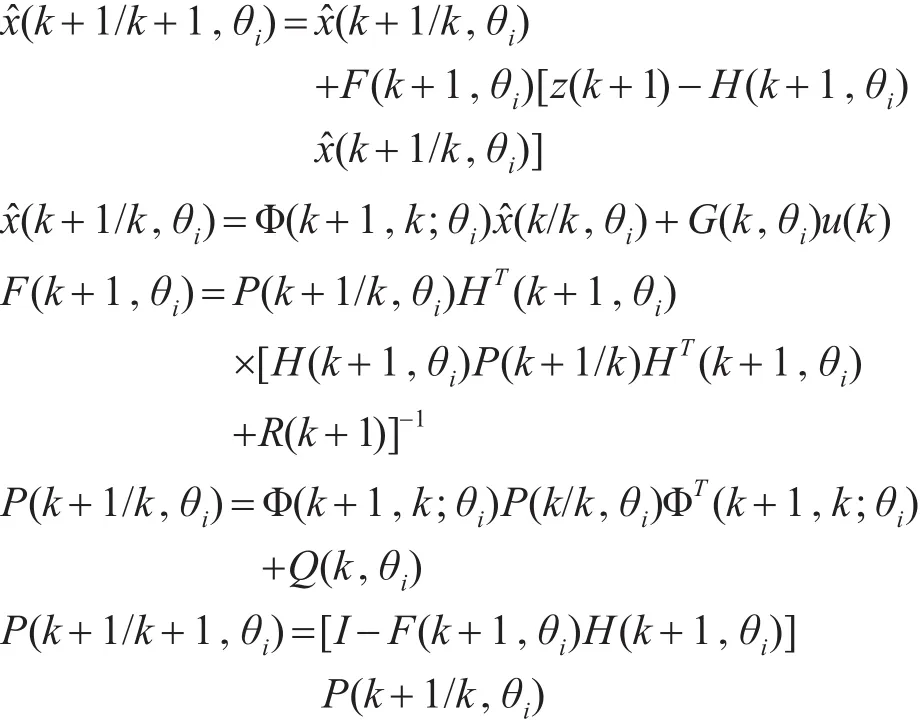
Step3：第i个模型后验概率的求解：

其中，

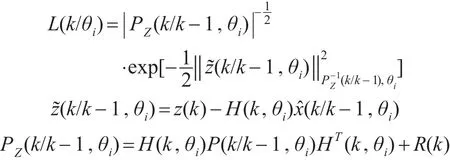
Step4：求出自适应控制器：

4 仿真分析

为了更好地验证本文算法的可行性，通过仿真实例来进行分析说明，并分别在两种情况下进行仿真：一种是参数为多模型未知参数，并且运行过程中参数不变；二是参数为多模型未知参数，但在运行过程中会发生切换。

考虑如下参数未知且为多模型的一阶系统：

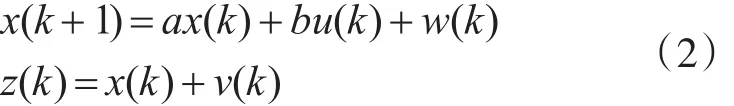
其中，未知参数a和b为常数。状态噪声和测量噪声w(k)和v(k)分别是均值为0，方差为σw2=0.25，σ2=0.04，高斯白噪声，步数N=100。性能指标

v

为：

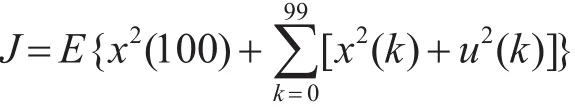
要做的就是寻找控制律u(k)，使上述性能指标最小。

1）多模型参数不发生切换：

模型不切换，认为参数模型一：a=0.8，b=0.5，为真实参数模型；

模型二为：a=0.4，b=1.0，为非真实参数模型。两个后验概率初始值都为0.5，仿真步数100步，后验概率仿真情况如图2所示。

图2后验概率图

从图2中可以看出两个模型开始的后验概率都是1/2，随着仿真步数的增加，真实参数模型一的后验概率逐渐趋近1，而非真实模型二的后验概率逐渐趋近于0，说明对偶自适应算法在针对不同模型有一定的识别能力。

当系统中的参数模型为已知的真实模型时候，对系统进行控制成为最优控制，图3是最优控制与多模型的控制率比较。

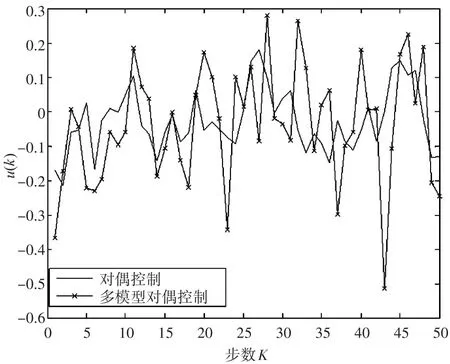
图3最优控制与多模型的控制率比较

图3是真实参数模型的经典LQG最优控制率与多模型基于后验概率的控制率的比较，可以看出，多模型后验概率基本和最优控制率形态保持一致，波动较大的原因为系统在识别参数模型时，需要有一定控制率进行识别控制，从而筛选出真实的参数。

2）多模型参数发生切换

基于仿真一多模型系统参数不切换的情况下，在此基础设定系统参数模型在运行过程中发生切换，当系统在运行过程中，参数模型不仅是一个有限集合，而且参数会发生切换，在基于上述仿真结果的前提下，设定真实参数不是一个定值，而是不断切换，为了更好的对上述情况进行对比，认为系统模型为式（2），参数在第二阶段发生切换，基于这种情况下，多模型自适应算法对这种情况同样进行分析，仿真步数为200步。

前100步：真实参数为模型一，取a=0.8，b=0.5，非真实参数为模型二，取a=0.4，b=1.0；

后100步：真实参数为模型二：取a=0.4，b=1.0，非真实参数为模型一：取a=0.8，b=0.5。

结果如图4所示。

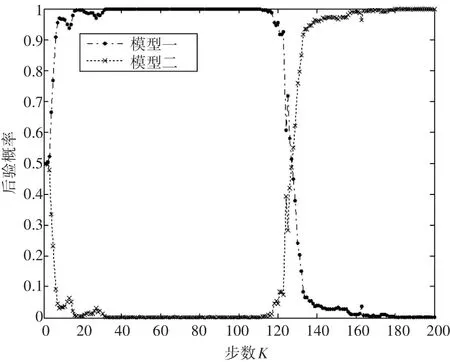
图4参数模型切换后验概率图

从图4中可看出来，100步之前，当系统真实参数为模型一，从图中看出，模型一的后验概率为随着仿真步数的增加，逐渐趋近于1，而非真实参数模型二的后验概率逐渐趋近于0；在100步之后，系统真实参数切换为模型二，非真实参数模型切换为一，从图中可以看出，经过短暂的调整之后，模型一的后验概率由原来的1又慢慢的趋近于0，而模型二的后验概率又逐渐趋近于1，可见此方法不仅可以对多模型参数系统中的真实参数进行识别，而且对于多模型参数切换的系统同样可以进行有效的控制识别。

5 结语

本文针对系统未知参数的多模型随机系统进行分析，通过传统的LQG模型的求解，加入后验概率来识别模型，针对每一个模型进行去求控制器时，就成为经典LQG问题，每个模型的控制器乘以它所对应的后验概率，最后在把每个模型的乘积加权在一起，就得出多模型未知参数随机系统的控制器。通过仿真图可以看出，系统的后验概率有很强的识别能力。

从仿真结果也可以看出，针对参数模型发生切换的情况，尽管在参数发生切换之后系统的后验概率能进行有效的切换更改，但是响应速度不够迅速，后续研究可从这方面入手进行进一步的优化。

［1］Li D，Qian F C，Fu P L.Optimal nominal dual control for discrete-time LQG problem with unknown parame-ters［J］.Automatica，2008，44（1）：119-127.

［2］D.O.Brian，etc.Twenty-five seminal papers in control［J］.IEEE control systems magazine，2002，20（1）：69-70.

［3］郭尚来.随机控制［M］.北京：清华大学出版社，1999：97-117. GUO Shanglai.Random Control［M］.Beijing：Tsinghua University Press，1999：97-117.

［4］Sokolov V F.Model evaluation for robust tracking under unknown upper bounds on perturbations and measurement noise［J］.IEEE Transactions on Automatic Control，2014， 59（2）：483-488.

［5］Deshpande J G，Upadhyay T N，Lainiotis D G.Adaptive Control of Linear Stochastic Systems［J］.IEEE Transac⁃tions on Automatic Control，1973，18（9）：107-115.

［6］He W G，Howard K，Rob R.Multiple Model Adaptive Con⁃trol Procedure for Blood Pressure Control［J］.IEEE Trans⁃actions on Biomed Eng，1986，33（1）：10-19.

［7］Watanabe K.A hierarchical Multiple Model Adaptive Con⁃trol of discrete-time Stochastic Systems for Sensor and Ac⁃tuator Uncertainties［J］.Automatica，1990，26（5）：875-886.

［8］Filipe N，Tsiotras P.Adaptive position and attitude-track⁃ing controller for satellite proximity operations using dual quaternions［J］.Journal of Guidance，Control，and Dy⁃namics，2014，38（4）：566-577.

［9］Li D，Qian F C，Fu P L.Variance minimization approach for a class of dual control problems［J］.IEEE Transactions on Automatic Control，2002，47（12）：2010-2020.

［10］杨恒占，高韵，钱富才.双重不确定随机系统对偶控制与RLS辨识控制比较分析［J］.西安工业大学学报，2016，36（10）：843-847. YANG Hengzhan，GAO Yun，QIAN Fucai.The analysis of dual control and RLS identification control for system with dual uncertainties［J］.Journal of Xi'an Technologi⁃cal University，2016，36（10）：843-847.

Dual Control Algorithm for System with Parameters Unknown

YANG HengzhanGAO YunFU Yueyuan
（School of Electronic and Information Engineering，Xi'an Technological University，Xi'an710021）

A multi-model dual control algorithm is presented for stochastic system with parameters unknown.Multiple models are used to describe the system model first，and then the integrate model is identified from multiple models via joining the posterior probability based on the LQG control theory.Finally，the integrate model is uesd to control the system.Simulation results illustrate the effectiveness of the algorithm.

stochastic system，dual control，multi-model

TP301.6

10.3969/j.issn.1672-9722.2017.07.004

2017年1月14日，

2017年2月17日

国家自然科学基金（编号：61273127）资助。

杨恒占，男，博士，讲师，研究方向：随机控制、最优控制、故障诊断等。高韵，女，硕士研究生，研究方向：控制理论与控制工程。付月园，女，硕士研究生，研究方向：控制理论与控制工程。