定数截尾样本下威布尔分布参数 ，γ，η 的贝叶斯估计

空军通信士官学校 黄娟娟

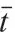
取（m，η，γ）的联合先验分布为：

一、参数m 的贝叶斯估计

对上式关于η，γ在（0，+∞）上积分后得到m的后验边际分布密度：

取平方损失函数：

其中，β=（β1，β2，β3）=（m，η，γ）为待估参数，d=（d1，d2，d3）为采取的决策。

由贝叶斯理论可知，在平方损失函数下，m的贝叶斯估计为：

由于β=（β1，β2，），L·（β），L（β）具有二阶混合偏导数，上式中的被积函数可化为eL·（β）与eL（β）的形式，则有近似公式：

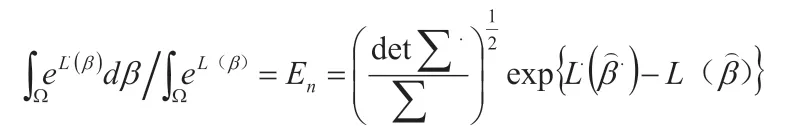
其中，Ω 为β的积分域， 分别为L·（β）和L（β）的最大值点。

综上，由近似计算公式求出参数m的估计。

二、位置参数γ 的贝叶斯估计

关于η，m在（0，+∞）上积分后得到γ的后验边际分布密度为：

其中，

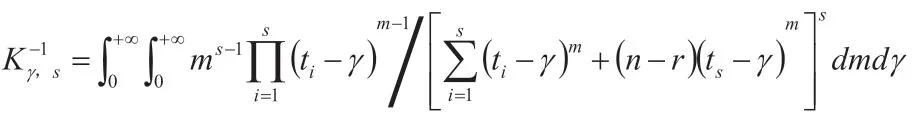
由上面两个式子在平方损失函数下，求得γ的贝叶斯估计为：

由此式及近似计算公式能求出γ的贝叶斯估计。

三、尺度参数η 的贝叶斯估计

关于m，γ在（0，+∞）上积分后得到η的后验边际分布密度为：

Γ（·）表示伽马函数，我们从上式可以很容易得到平方损失下η的贝叶斯估计：

由上式运用近似计算公式可求出η的贝叶斯估计。