基于次分数Black-Scholes模型的欧式期权定价*
2021-11-04靳晨萱霍海峰
靳晨萱,霍海峰,温 鲜,徐 东
(1.广西科技大学 理学院,广西 柳州 541004;2.中国银行股份有限公司 侯马支行,山西 侯马 043000)
0 引言
期权作为常见的金融衍生产品之一,在交易过程中可以给投资者带来丰厚的利润,但也存在着潜在的经济危机.因此,选择合理的数学模型预测期权价格对于投资者的风险控制至关重要.1973年Black和Scholes[1]建立Black-Scholes(B-S)模型以来,期权定价问题得到了广泛的研究,也为广大投资者进行风险控制提供了一些理论决策依据.然而大量实证研究[2,3,4]表明,股票价格变动具有长程相关性等特点,这与经典B-S模型中股票价格服从几何布朗运动的假设不相符.为了更贴近交易市场中股票价格的波动趋势,许多学者改进了经典B-S模型,建立了不少新模型,如基于分数布朗运动[5]、双分数布朗运动[6]、混合分数布朗运动[7]等驱动的定价模型.
近年来,Bojdecki等[8]提出的具有自相关性、长记忆性等特点的次分数布朗运动得到了许多学者的广泛关注.次分数布朗运动作为布朗运动的进一步扩展,不仅能够刻画资产价格变动的长程相关性质,而且其增量是非平稳的.Tudor[9]、Wang Zhi[10]、Yan等[11]分别围绕次分数布朗运动的长记忆性、随机积分和It公式开展研究,并基于次分数布朗运动建立更贴合金融市场的期权定价模型.随后,许多学者在此模型下开展期权定价研究,例如,两值期权[12]、亚式期权[13]、广义交换期权[14]等研究.但是这些期权所采用的主要定价技术是偏微分方程方法,具体来说,叶方琴[12]等利用变量代换和偏微分方程研究了两值期权定价问题;张亚芳[15]、肖炜麟等[16]、程志勇等[17]应用偏微分方程方法建立欧式期权价格的显示解.针对欧式期权定价问题,不同于文献[17],本文基于次分数Black-Scholes模型,从理论推导采用概率方法和数值计算采用二叉树法来对欧式期权进行定价,使得期权定价的计算更加简捷有效.
本文针对标的资产满足次分数Black-Scholes模型,研究无红利支付的欧式期权定价问题,首先,以次分数布朗运动为基础建立股票价格满足的次分数Black-Scholes 随机微分方程.其次,利用次分数伊藤公式求解得到股票价格变化满足的关系式,进而利用概率方法得到欧式看涨期权价格的显示解.最后,以国电JTB1权证为例,估计模型参数,计算期权理论价格,并将计算结果与经典B-S模型、二叉树模型以及实际价格进行比较,进一步说明次分数B-S模型和二叉树模型定价结果的合理性和有效性.
1 次分数 Black-Scholes 模型
1.1 预备知识
定义1 次分数布朗运动是Hurst指数为H(H∈(0,1))的连续高斯过程{ξH(t),t∈R}=0,其期望值E[ξH(t)]等于零,其协方差为
当H=1/2时,次分数布朗运动为标准布朗运动.
定义2 设变量X(t)={X(t),t≥0}服从以下伊藤过程:
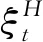
(1)
1.2 次分数 Black-Scholes 模型
考虑在一个无套利机会的完备市场中,标的资产服从次分数布朗运动,则在风险中性概率测度Q下股票价格S满足随机微分方程
(2)
令a=μS,b=σS,则由式(1)可得t时刻股票价格
(3)
其中r为无风险利率,σ为波动率,St0为初始时刻t0的股票价格.
2 主要结果
下面以欧式看涨期权为例,利用概率方法推导得出其价格显示解.
定理1 当股票价格满足次分数Black-Scholes模型(2)时,无红利支付的欧式看涨期权在t∈[0,T]时刻的价格为
C=StN(d1)-Ke-r(T-t)N(d2),
(4)
其中K为行权价格,T为到期日,N(·)为标准正态分布函数,
证明由欧式看涨期权收益函数为(ST-K)+=max{ST-K,0}和概率法可知,在t∈[0,T]时欧式看涨期权价格为
C=e-r(T-t)EQ[(ST-K)+]=e-r(T-t)EQ[STI{ST≥K}]-e-r(T-t)EQ[KI{ST≥K}]=E1-E2.
(1)由公式(3)可得
其中,
(2)类似地,由公式(3)可得
E2=e-r(T-t)EQ[KI{ST≥K}]=Ke-r(T-t)N(d2),

定理2 当股票价格满足次分数Black-Scholes模型(2)时,无红利支付的欧式看跌期权的到期执行价格为
P=Ke-r(T-t)N(-d2)-StN(-d1),
其中d1,d2同定理1.
证明类似于定理1可证.
3 数值分析
下面以2008年5月22日至2010年5月14日国电JTB1权证数据为例进行实证分析(表1数据来源于国泰安数据库).

表1 国电JTB1权证部分数据
3.1 次分数B-S模型参数估计
当股票价格满足次分数 Black-Scholes 模型(2)时,为了验证公式解(4)的可行性和有效性,首先结合实证数据进行参数估计,参考文献[16]建立σ、H的如下估计:
(5)
(6)
其中h为观测时间间隔,Y=(Yh,Y2h,…,YNh)'.
由图1可看出,对比经典B-S模型,次分数B-S模型的期权价格模拟值更接近于实际价格.由表2统计结果可知,对比经典B-S模型,次分数B-S模型的期权价格均值、最小值与实际期权价格较为接近,且其标准差比实际价格更小,说明次分数布朗运动环境下的欧式期权定价具有很好的参考意义.
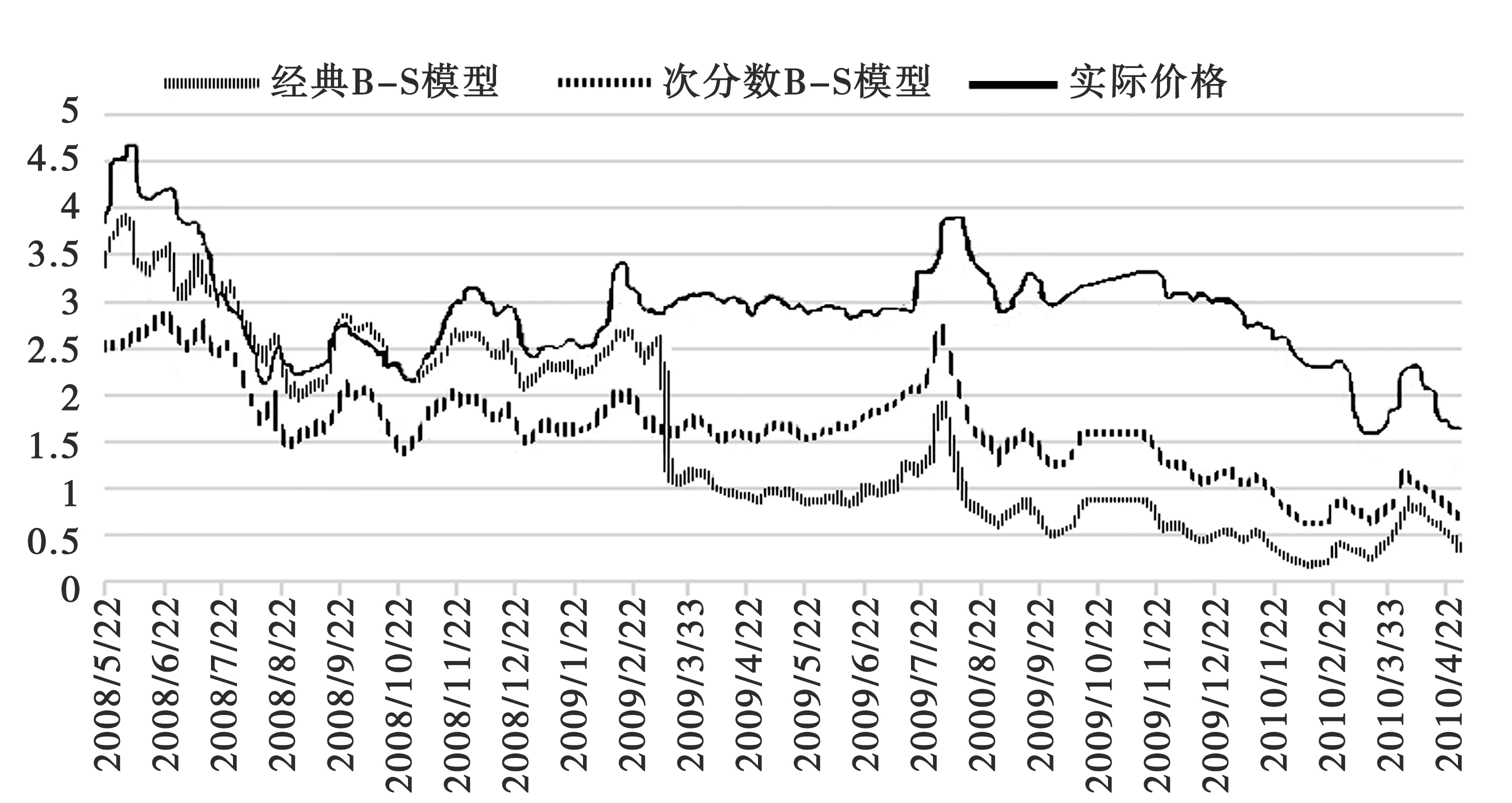
图1 B-S模型计算结果与真实价格走势比较图
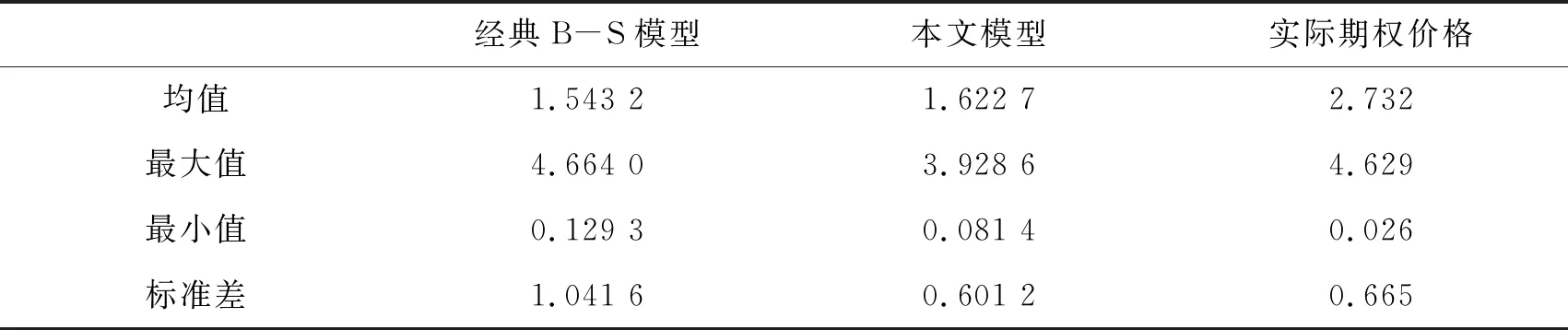
表2 股票价格描述性统计
3.2 二叉树模型计算模拟

er(2-22H-1)t2H=pu+(1-p)d,σ2(2-22H-1)t2H=pu2+(1-p)d2-[pu+(1-p)d]2,

利用u、d、p三个参数值可以模拟出单步二叉树的期权价格,并与次分数B-S模型的期权价格和实际价格进行比较,如图2.
由图2知,二叉树模型的模拟价格与实际价格波动大致相符,次分数B-S模型计算的期权价格比二叉树模型的期权价格高,且其计算结果更加接近实际价格.

图2 二叉树模型计算价格与实际价格走势比较图
3.3 误差分析
令Pi和Qi分别为模型的计算值和实际值,使用相对误差来精确分析不同定价模型的误差.
Rel_error=|(Qi-Pi)/Qi|.
进一步,计算当T=1/2、T=1/4、T=3/4时不同模型期权价格以及相对误差,如表3所示.
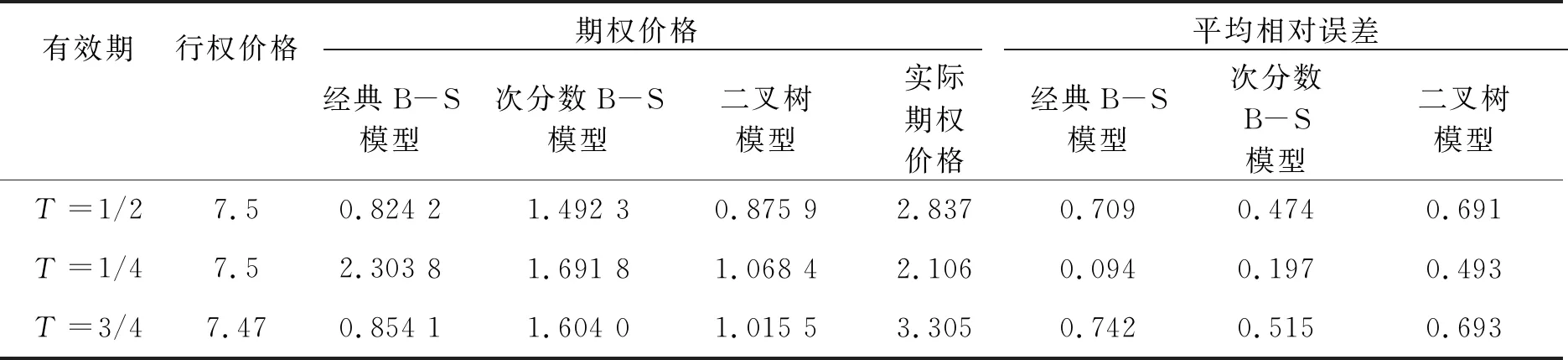
表3 不同模型的误差分析表
表3分别比较不同有效期内,经典B-S模型、次分数B-S模型、二叉树模型与实际价格的平均相对误差.误差分析表明:次分数B-S模型的计算结果更加接近实际价格,其次为二叉树法模型,最后为经典B-S模型.这表明基于次分数B-S模型描绘期权价格变化趋势更加贴近真实的金融市场情况,更具实际价值.
4 结论
选择合理的期权定价模型预测期权价格是决策者进行期权交易时规避风险的重要手段.为解决经典B-S模型与实际金融市场不相符的严格假设问题,本文采用具有长程相关性的次分数布朗运动来描述股票价格变动,讨论次分数Black-Scholes模型下欧式期权定价问题,并结合次分数伊藤公式以及概率方法计算欧式看涨期权价格的显示解.最后,以国电JTB1权证数据为例,计算理论模型的期权价格,并分别与经典B-S模型、二叉树模型与实际价格进行比较,验证模型的有效性和可行性,结果表明:基于次分数Black-Scholes模型能更准确反映股票价格变动情况,有助于期权持有者在交易市场中更加有效地进行风险控制.
