关于丢番图方程x4-q4=py5*

管训贵

(泰州学院 数理学院，江苏 泰州 225300)

0 引言及主要结论

设Z,N*,P分别表示整数集、正整数集和奇素数集.熟知，方程

x4-q4=pys，x,y∈N*，p,q,s∈P，gcd(x,y)=1

(1)

是一类基本而又重要的丢番图方程,由于它与著名的广义Fermat方程有关(见文[1-4]),因此判别(1)是否有解,是一个非常困难的问题,目前仅有一些零散的结果.

2010年,Luca和Togbé[6]运用椭圆曲线整数点的存在性证明了:s=3时,方程(1)没有解.

2013年,刘艳艳[7]运用Lucas数的算术性质证明了:如果s>3且p≡3(mod 4),则(1)没有解(x,y,s)适合2⫮y.

本文运用同余理论和代数数论的有关结论证明了如下定理.

定理1 设p,q均为奇素数，且p≡3(mod 4)，则丢番图方程

x4-q4=py5，x,y∈N*，gcd(x,y)=1

(2)

此定理改进了文[5]中的结论.

1 若干引理

引理1[8]设M是唯一分解整环，2≤k∈Z，α,β∈M，gcd(α,β)=1.若αβ=γk，γ∈M，则

α=ε1μk，β=ε2νk，μ,ν∈M，

这里ε1,ε2是M中的单位元素，并且ε1ε2=εk，ε也是M中的单位元素.

引理2[9]设p是一个奇素数，则方程x4-py2=1除p=5,x=3,y=4和p=29,x=99,y=1820外，无其他的正整数解.

引理3[7]若s>3且p≡3(mod 4),则(1)没有解(x,y,s)适合2⫮y.

2 定理的证明

设(x,y)是(1)的一组解.若p=q，则q|x，进而q3|y5，从而q|y，与gcd(x,y)=1矛盾，故p≠q.

由p≡3(mod 4)知p⫮(x2+q2).于是p|(x+q)或p|(x-q)，且gcd(x,q)=1.

情形Ⅰ2⫮x

此时2‖(x2+q2)且x-q,x+q中必有一个模4余2，故由式(1)可得

x+q=8pw5，x-q=2u5，x2+q2=2v5，

(3)

或

x-q=8pw5，x+q=2u5，x2+q2=2v5，

(4)

这里u,v,w两两互素，y=2wuv.

根据引理1，在Z[i]中，(3)或(4)的第三个方程可写成

(x+qi)(x-qi)=i(1-i)2v5.

(5)

设δ=gcd(x+qi,x-qi)，则δ|gcd(2x,2qi)=2，即δ可能取值1，1-i，2.若δ=1，则i(1-i)2=2一定只能整除x+qi或x-qi中的一个，但这是不可能的；同样δ=2也不可能.所以必有δ=1-i.由此及式(5)得

故有

x+qi=(1+i)(a+bi)5，a,b∈Z，

即

x=(a-b)[(a-b)4-20a2b2]，

(6)

q=(a+b)[(a+b)4-20a2b2].

赫施在《解释的有效性》中说：“没有人能够确定地重建别人的意思，解释者的目标不过是证明某一特定的读解比另一种读解更为可能罢了。在阐释学中，证明即是去建立种种相对可能性的过程。”

(7)

由q为素数及式(7)知，(a+b)4-20a2b2=±1或a+b=±1.

当(a+b)4-20a2b2=±1时，q=±(a+b).对(a+b)4-20a2b2=-1两边取模4知(a+b)4≡-1(mod 4)，这不可能.因此(a+b)4-20a2b2=1，q=a+b>0.根据引理2，方程X4-20Y2=1即X4-5(2Y)2=1仅有整数解(X,Y)=(±1,0)和(±3,±2)，所以

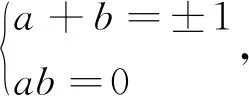
解之得(a,b)=(2,1)或(1,2).从而q=3，x=79.但794-34=24·55·19·41,不合题意，故此时(1)没有解.

当a+b=±1时，q=±(1-20a2b2).考虑到对于q>1，有a+b=-1，即b=-a-1,所以

q=20a2b2-1=20a2(a+1)2-1=20a4+40a3+20a2-1，

(8)

x=(2a+1)[(2a+1)4-20a2(a+1)2]=-8a5-20a4+20a2+10a+1.

(9)

由式(9)可得x=-4a4(2a+5)+10a(2a+1)+1.因为x>0，故有a≤-3或0≤a≤1.又当a=0时，q=-1，不合题意；当a=1时，q=79，此时x=3，但34-794=-24·55·19·41,也不合题意，所以只能有a≤-3.

令a=-m，则式(8)、式(9)成为

q=20m2(m-1)2-1=20m4-40m3+20m2-1，

(10)

x=8m5-20m4+20m2-10m+1,

(11)

这里3≤m∈Z.

(12)

但当m≥3时，可推出式(12)不成立.因此q

情形Ⅱ2|x

此时2⫮y.根据引理3，在此情形时方程(1)没有解.

定理得证.

说明:对于一般情形，若p≡3(mod 4)，2|y,则有

x+ηq=2us，x2+q2=2vs，η∈{±1}， gcd(u,v)=1.

(13)

将(13)的前两式相乘得

(x+ηq)(x2+q2)=4(uv)s.

(14)

令X=ηx/q，Y=ηuv/q，则式(14)成为

(X+1)(X2+1)=4Ys.

(15)

因此，(1)是否有解最终归结为超椭圆曲线(15)是否有有理解.