二维离散切换系统的稳定性

秦 雪

(重庆工程学院 通识学院，重庆 400056)

0 引言

Roesser[1]提出了著名的二维离散系统模型，用以研究线性图像处理问题.到目前为止，已有许多学者对二维系统的稳定性进行了广泛的研究[2～5].值得注意的是，在整个系统中，模态被激活的概率有的很大有的很小，而那些不易被激活的模态对系统动态行为的影响非常小.因此，在研究这类系统的稳定性问题时有必要引入转移概率.

1 模型介绍

考虑如下的二维离散切换系统:

(1)

其中x(i,j)∈n是系统的状态向量，y(i,j)∈ny是测量输出,u(i,j)∈nu是控制输入.γ(i,j):+→{1,2,…,m}=Μ为分段常值函数，其中m>1表示模态的个数.和Cγ(i,j)都是具有适当阶数的常数矩阵.对时间序列ks,s∈+,有∞,系统的初值条件为+,且满足等式和边界条件

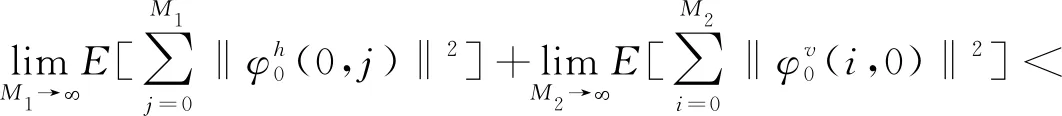
本文需要以下假设条件：

假设1 切换信号γ(i,j)只与i+j有关.当i+j=k时简记γ(i,j)为γk.

若切换信号γk=p∈Μ,k∈[ks-1,ks),s∈+，则dp(s)∶=ks-ks-1<∞表示γk第s次切换到模态p时的驻留时间，它是随机正变量，即E[dp(s)]=ϑp>0，且当p≠q时dp(s)与dq(s)相互独立.记θpq为γk从模态p切换到模态q的转移概率(TP)，即

θpq∶=Prob{γks+1=q|γks=p}.

假设2 转移概率矩阵Θ∶=(θpq)m×m不可约.根据文献[6]，此时Θ存在唯一的平稳分布π=(π1,π2,…,πm),且它满足

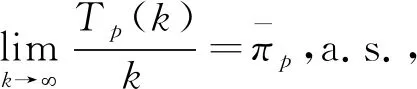
设计依模态的输出反馈控制器如下：

u(i,j)=Kγ(i,j)Cγ(i,j)x(i,j),

(2)

其中Kγ(i,j)∈nu是控制增益.

将(2)代入系统(1),可得以下闭环系统:

(3)

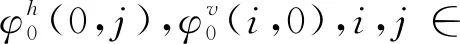
则称系统(3)是渐近稳定的，其中ξT(k)=(xT(i,j+1)，xT(i+1,j)).

本文的目的是证明闭环系统(3)的渐近稳定性.

2 主要结果

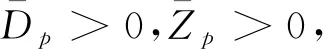
(4)

(5)

(6)

则系统(3)是渐近稳定的.

证明设i+j=k∈[ks-1,ks)⊂+,γ(i,j)=p∈Μ.构造如下的Lyapunov泛函:

(7)

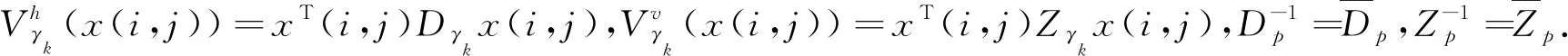
由式(7)可得

(8)

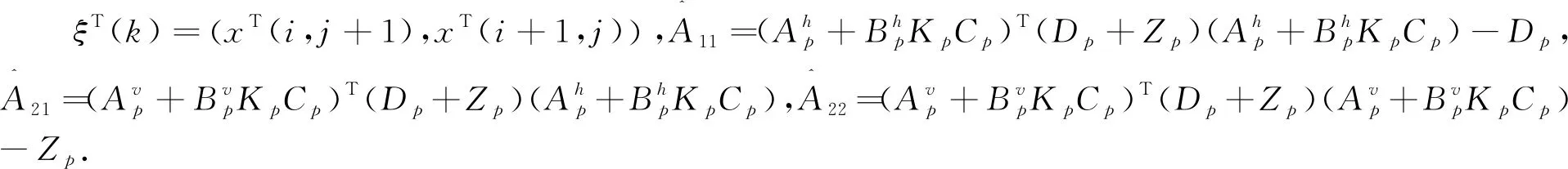
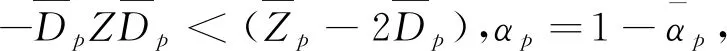
于是有

故有

当i+j=k∈[ks-1,ks)时，

(9)

对∀i+j=k∈+,k∈[ks-1,ks),根据式(5)和式(9)可得

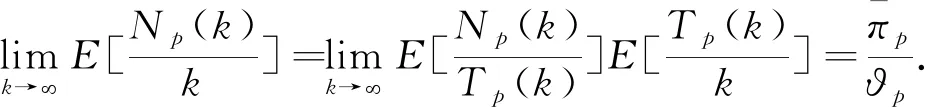
由条件(6)可得以下不等式：

3 数值模拟

令Μ={1，2，3}，考虑系统参数为

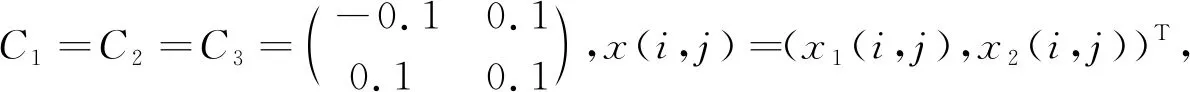
由图1和图2可见系统(3)是渐近稳定的.

图1 闭环系统中状态x1(i,j)

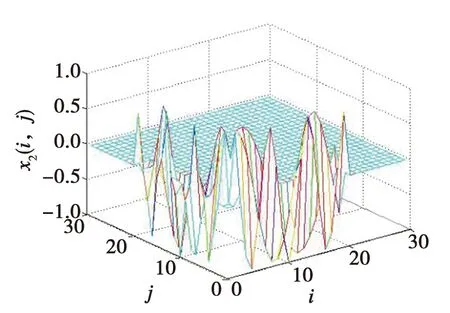
图2 闭环系统中状态x2(i,j)

4 小结

本文通过线性矩阵不等式给出了一个保证闭环系统(3)渐近稳定的充分条件，然后通过数值模拟验证了该结果.