谱体积方法单元分割与问题单元标记方法的改进研究
2021-11-02柯耀祖
柯耀祖, 张 兵
(合肥工业大学 机械工程学院,合肥 230000)
1 引 言
基于TVD性质发展的传统有限体积法是计算流体力学中的重要方法,广泛应用于各大商业CFD软件和研究代码中,但其计算精度与网格划分密切相关,往往需要极大的网格数量才能得到网格收敛解。尽管网格自适应方法一定程度上可解决上述问题,但针对激波和接触间断处于运动状态的非定常计算问题,不但会导致计算量剧增,还存在难以解决的并行负载平衡问题[1]。
谱体积方法(SVM)是一种从本质上解决求解器对网格依赖性的高精度方法,其基本原理是将一个网格单元(简称谱体积元SV)按精度需要分割成多个内部控制体(简称CV),并假设谱体积内变量的空间分布为控制体平均值的多项式函数,进而采用传统有限体积方法对方程进行空间和时间离散,并求解得到具有高阶精度的解。由于谱体积元内部精度可按需要提高至任意阶,故该方法可实现在任意密度网格上获得网格收敛解[2]。谱体积方法由Wang[3]首次提出并应用于一维Euler方程求解,随后推广到二维及三维问题[4-7]。为了进一步满足不同问题求解需求,Liang等[8]对谱体积方法进行扩展,如N-S方程的多重网格方法。Breviglieri[9]通过一种基于双曲守恒定律的空间离散方法,实现对流场问题的高精度求解。高精度格式是现在CFD方法的研究热点,侯冶[10]研究了一维SVM方法,并与有限差分法对比验证SVM的高效性。郑华盛等[11]基于谱体积方法思想,通过筛选出适当的单元组成模板,利用WENO重构方法和有限体积法,构造出适用于非结构网格二阶和三阶精度的有限体积WENO格式。针对多物理耦合计算耗费过大,刘娜等[12]设计出适合多介质流动模拟的谱体积方法。值得说明的是,由于N-S方程的特征决定了其解的形式是非光滑的,特别是对于存在激波的问题,谱体积方法的多项式假设必然会导致解的震荡,需要采用合适的控制体分割方法、限制器函数及问题单元标记方法进行处理,三者决定了SV方法的稳定性和精确性。van den Abeele等[13]提出通过傅里叶分析检测分区质量和色散误差,来确定非结构网格单元的稳定性;Lamouroux等[14]提出一种基于空间加权投影的高阶限制器;Hadadian Nejad Yousefi等[15]则提出了一种基于WENO方案的切比雪夫SV方法,用于求解一维和二维的守恒定律方程。
由于切比雪夫多项式的正交性、奇偶性和有界性,其在连续函数逼近问题中得到广泛应用,如能最大限度地降低龙格现象,可以提供多项式在连续函数的最佳一致逼近等,因此本文提出一种采用切比雪夫多项式确定非结构网格单元的内部控制体划分方法。同时,为防止不连续区域在求解过程中数值发散,在minmod TVB限制器[16]基础上,采用参数自由的广义限制器,通过标记单元和限制标记问题单元这两步骤,以保证平滑区域的精度和避免不连续区域的解振荡。最后,通过二维Euler方程的典型算例进行验证。
2 谱体积方法
积分形式的Euler方程为
(1)
式中t为时间,Ω为计算域,Q为守恒变量,F为无粘通量。
将求解域离散成N个不重叠谱体积单元,即
(2)
根据有限体积假设,对于任意谱体积单元,式(1)可改写为
(3)

对二维问题,为了达到k阶精度,需要将谱体积元SVi分成m=k(k+1)/2个控制体CV(3.1节),任意控制体CVi ,j的守恒变量平均值可表示为
(i=1,…,N;j=1,…,m)(4)
式中Vi ,j为控制体CVi ,j的体积。
当SVi内所有控制体的平均守恒变量已知时,可以重构出一个(k-1)次多项式Pi(x,y),以k阶精度在SVi内逼近Q(x,y)。
Q(x,y)=Pi(x,y)+O(hk -1)
(5)
式中多项式Pi的系数由控制体的守恒变量均值表达。此高阶重构多项式用于计算SVi内任意位置处的守恒变量值。
对控制体CVi ,j,方程(1)可写为
(6)

采用k阶高斯数值积分方法对式(3)进行面积分可得
[Q(xr q,yr q)]Ar+O(Arhk)
(7)
式中J=(k+1)/2为每个面上的积分点数目,ϖr q为高斯积分权重,(xr q,yr q)为积分点坐标。
由于在每个SVi内部守恒变量分布满足多项式假设,故在SVi内的控制体交界面上的通量F直接采用解析表达式计算。而在谱体积之间的交界上,由于变量的重构结果并不相同,故需要采用迎风格式计算,本文采用基于Harten熵修正方法[17]的Roe格式。
3 分区方法和限制器
3.1 谱体积单元的分区
插值多项式Pi(x,y)的性能是由形函数Li ,j(x,y)决定的,而Li ,j(x,y)又是通过CVi ,j单元的划分计算得到。一般来说,可以采用任意分区方法,但是不恰当的分区方法可能会导致结果振荡,降低计算精度[18,19]。因此,一个良好的分区方法是保证高精度数值计算的前提。
为提高模拟过程的稳定性和精确性,van den Abeele[13]和Wang[5]详细探讨了二维谱体积单元的划分方法。在此基础上,本文提出使用基于切比雪夫多项式[20]的分区方法,以保证计算结果的收敛性。以一维SV方法为例,对任意一个谱体积单元,建立单元局部坐标系x∈[-1,1],其分区过程如下。
(1) 将切比雪夫多项式的根作为控制体的形心,
(k=0,1,…,n-1)(8)
式中xk为切比雪夫多项式的根,n为计算精度。
(2) 通过xk确定所有CVi ,j的边界,得到所有CVi ,j边界面的位置为
f1=-1,fn +1=1,fk +1=f1+2|xk|
(k=1,…,n)(9)
式中f1和fn为SVi外部边界面,fk为SVi内部边界面。
(3) 如果阶次n是偶数阶,则先确定SVi靠近外侧的内部边界面,即
f1=-1,fn + 1=1,fk + 1=2xk-fk
fn + 1 - k=2xn + 1 - k-fn + 2 - k
(k=1,…,n/2)(10)
通过上述的三个步骤确定最终的通量面位置,如 图1 给出的就是一维CVi ,j边界面的分布。
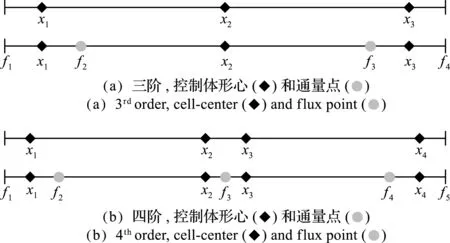
图1 一维S V单元分区和通量点的位置
对于二维非结构网格的任意谱体积元,采用面积坐标定义分割点位置,将切比雪夫多项式的根作为SVi三个边界面上数值点xk,然后根据xk求出面通量位置,图2为2阶和3阶SVi单元的分割结果,其中,xk为切比雪夫多项式的根,而fk则为控制体边界在谱体积元面上的位置。

图2 二维S V单元分区
对于四阶及四阶以上的偶数阶精度,和一维类似,先确定外侧控制体边界的位置,再逐步确定内部控制体的边界。
3.2 限制器函数
对于Euler方程,如果解存在间断或不连续,则需要在通量积分点处进行限制,以保证数值稳定性和收敛性。本文将限制器计算过程分为两部分,首先找到并标记出需要限制的问题单元,然后对该单元上的所有积分点处的变量进行限制。在后一过程中,采用泰勒级数展开重构谱体积单元平均化导数[21],然后从最高阶导数到最低阶导数限制问题单元。如果最高阶导数不受限制,则取消该单元的标记。这种限制器能够在保证平滑区域精度的前提下,有效地抑制不连续区域附近的振荡。
与已有研究方法不同,Wang等[5,6]是直接通过任意谱体积的相邻谱体积单元来判断该谱体积单元是否需要限制,而本文使用的单元标记都是在控制体单元内进行的,但是限制却在谱体积单元中展开。这是由于一旦控制体单元标记为问题单元,那么当前控制体所属的谱体积元的插值多项式不再继续适用。本文使用的限制器是基于ENO和WENO方法改进的TVB标记方法,以三阶精度为例,将限制和重构的过程分为以下几个阶段。
(1) 对于任意一个控制体单元,采用Q表示其任一主变量(ρ,u,v,p),首先计算出该单元与其共面的所有相邻单元中的最大值和最小值主变量。
(11)
(2) 如果当前控制体单元中给的任一积分点处的变量满足以下条件,则初步认为这个单元为问题单元。
Qi(xr q,yr q)>1.001Qmax,i
Qi(xr q,yr q)<0.999Qmin,i
(12)
式中下标rq表示积分点。
(3) 上述的标记规则过于严格,可能得到很多非问题单元。因此,本文通过改进后的minmod限制器函数判断最终需要限制的问题单元。
① 定义从当前CVi ,j形心到与其共面的相邻控制体形心的方向矢量为
l=lxi+lyj
(13)
则CVi ,j和邻居控制体这个方向上的一阶和二阶导数定义为
Ql ,i=Qx ,ilx+Qy ,ily
Ql ,neigh=Qx,neighlx+Qy ,neighly
(14)
式中下标neigh表示邻居控制体,Qx,Qy,Qx x,Qx y和Qy y是CVi ,j的一阶和二阶偏导数,可通过求解二次方最小二乘重构[22]得到。
(15)
式中r为SV的体心位置。
② 对该面上积分点处的物理量,采用式(16)进行初步限制。
(16)
式中下标k为控制体的面编号,β取1.5。
③ 循环CVi ,j所有面,计算CVi ,j的标量限制器最小值,即
(17)

Qx y(ΔxΔy-Ix y)]
(18)
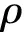
4 算例验证
通过两个算例结果验证本文的分区方法和限制器性能,所用的时间积分全部为隐式LU-SGS方法。
4.1 15°压缩拐角超声速流动
第一个算例是NASA算例库的15°压缩拐角超声速流动算例[23],其中来流边界位于左侧x=-0.3左,右侧出口边界位于x=0.5,计算域高度取0.75,马来流马赫数为2.0,采用疏密不同的计算网格进行求解,以便对比不同方法的计算性能。其中,图3(a)的网格用于谱体积法和常规有限体积法(简称FVM)求解,单元数量为1137。图3(c,d)仅使用FVM求解,单元数量分别为4633和18731。图3(b)展示的则是三阶精度下,划分控制体后的网格。
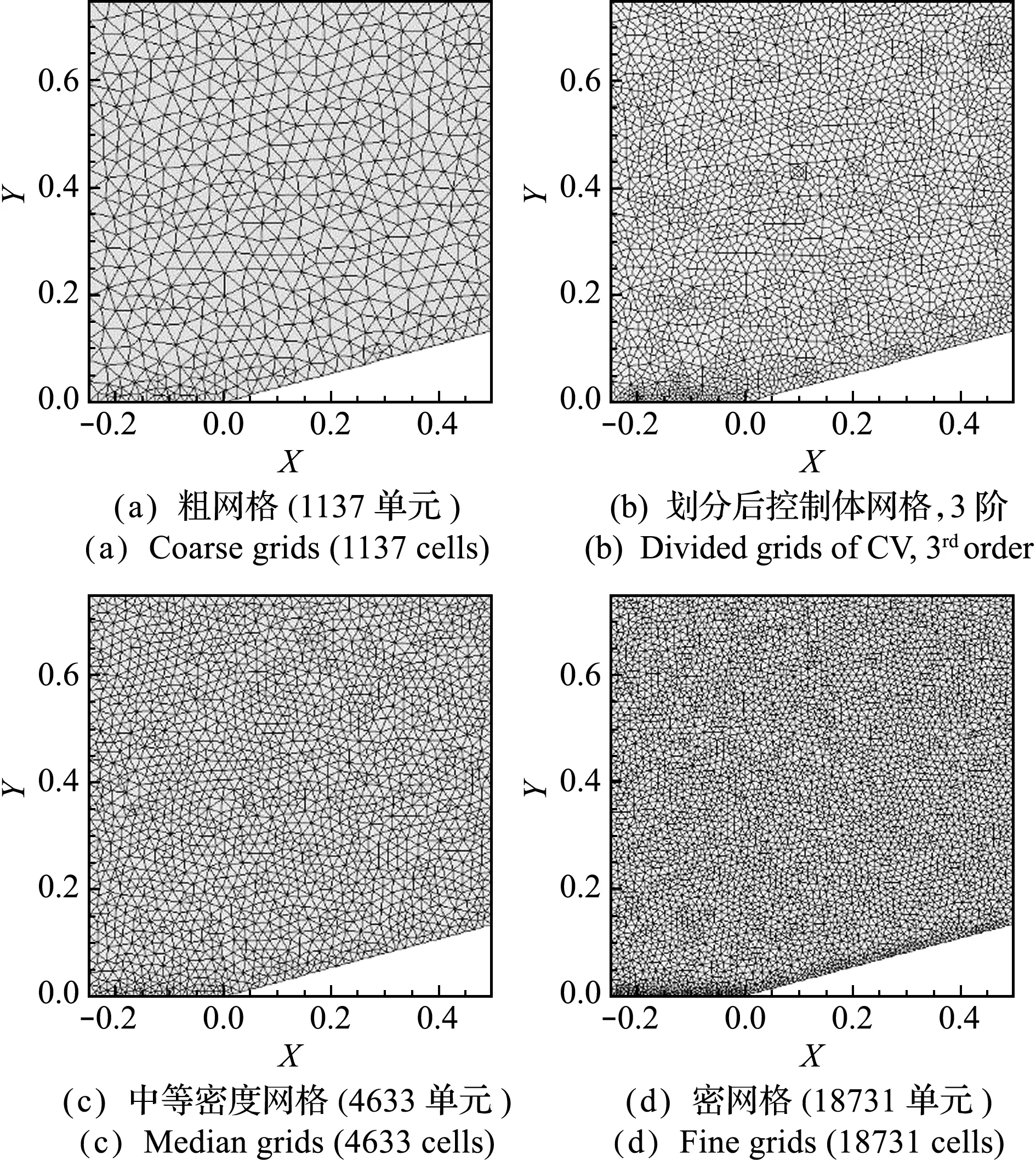
图3 不同密度的计算网格
如图4为物面压力系数分布结果曲线,可以看出,粗网格下SVM和密网格下FVM的求解结果吻合较好,计算得到的激波比粗网格FVM结果更陡峭。值得一提的是,SVM仅使用1137个谱体积元(6822个控制体元),而FVM则使用18731个网格。
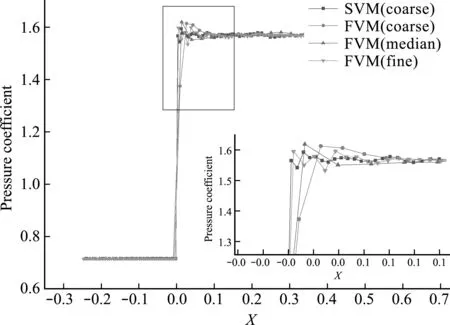
图4 SVM和FVM的压力系数分布曲线对比
图5展示的是在相同网格数条件下,采用改进后的控制体分割方法和使用Wang等[5]提出的分区方法计算结果与密网格下FVM计算结果的对比,可以看出,本文方法的激波更陡。

图5 不同分区方法的压力系数计算结果
图6(a)为三阶SV方法计算得到的楔形板压力分布情况。采用改进后的限制器,只对激波区域的谱体积单元进行标记和限制,如图6(b)所示,激波处的黑色单元为标记的问题单元,其出现的位置全部位于激波位置处,故可有效识别不连续区域。
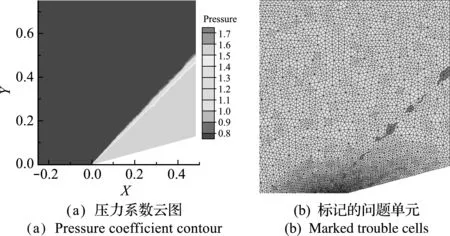
图6 15°楔形板的超音速流,3阶
4.2 NACA0012跨音速流
第二个算例是Yang等[16]的NACA0012跨音速流算例,其中翼型展长为1,来流马赫数为0.8,迎角1.25°,分别采用三种不同密度网格进行计算,网格单元数量分别为5128,9814和20880。采用如图7(a)所示的粗网格用于SVM和FVM求解,图7(c,d)仅使用FVM计算,图7(b)为二阶谱体积元内部的控制体单元划分情况。图8为翼型表面的压力系数分布,可以明显看出,粗网格下的FVM结果激波过于平滑,说明网格密度对FVM求解的精度影响较大。粗网格下SVM方法得到的压力分布与密网格下FVM结果吻合较好,说明SVM方法大大降低了网格需求。另一方面,通过对相同网格数下不同分割方法计算结果的对比可以发现,相比于Wang[5]的分割方法,采用切比雪夫多项式划分谱体积元的方法得到的激波更陡峭。

图7 NACA0012机翼流场网格
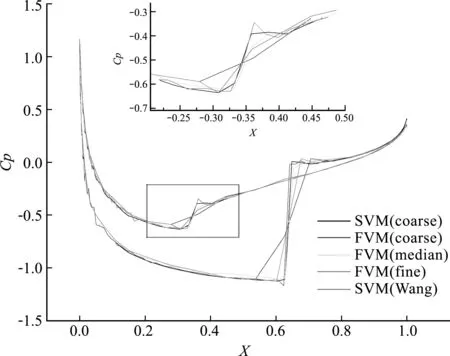
图8 SVM和FVM以及不同分割方法的的压力系数分布
为清楚观察标记的问题单元,只放大机翼周围的单元,图9(a)为使用三阶SV方法求解获得的马赫分布图,图9(b)给出标记问题单元的位置在上下表面激波处。测试结果表明,本文采用的分区方法和限制器可以有效标记激波不连续区域,并对其进行合理限制。
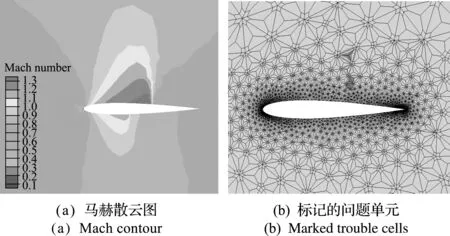
图9 NACA0012机翼的跨音速流
4.3 计算效率分析
尽管SV方法在一定程度上减少了求解器对网格的依赖性,降低了CFD分析时间,但其基本原理决定了SVM在求解过程中需占据更多的计算资源。表1为相同网格数下三阶SVM和FVM的计算效率对比,其中第一行为FVM计算时间,而第二行为SVM的计算时间。所有程序由C++语言编写,并在i7-8750H,2.20 GHz处理器上完成测试。
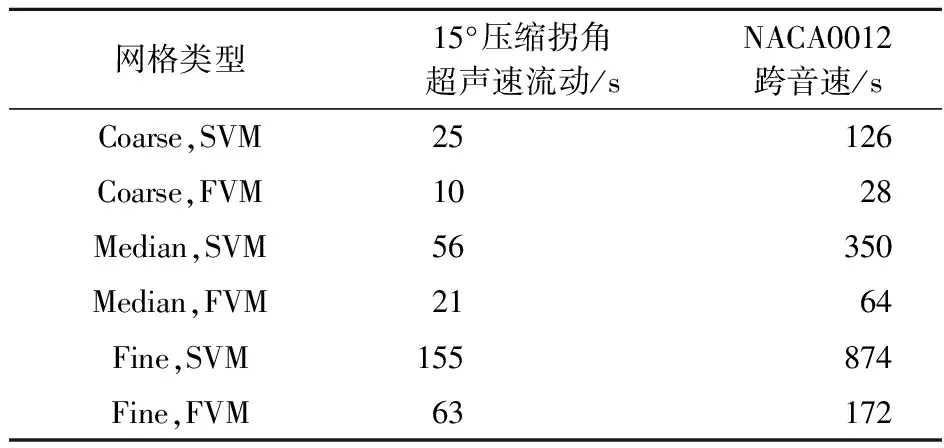
表1 SVM和FVM计算时间对比
由表1可知,在相同网格数条件下,SV方法需要的计算时间大于传统的二阶FVM;对本文算例而言,在满足相同精度条件下,粗网格下的SVM计算时间大致与4倍网格密度下的FVM相当。
5 结 论
(1) 建立了基于切比雪夫多项式方法的谱体积分割方法,典型算例表明,该方法具有更好的计算精度。
(2) 发展了基于WENO的变量限制方法,以及综合考虑谱体积和控制体的问题单元标记方法,以有效识别不连续区域。
(3) 采用二维可压缩Euler方程典型算例验证了上述方法的有效性。结果表明,采用较少的网格即可获得与数倍密网格下传统有限体积法相当的计算精度,并具有较好的计算效率。
