基于数值流形方法的特殊孔缘单元构造及开孔板求解

武卓威， 刘 俊*

(1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.上海交通大学 高新船舶与深海开发装备协同中心，上海 200240)

1 引 言

开孔在各类工程结构物中较为常见，如船体结构内部通常设有人孔、流水孔、透气孔和减轻孔等。这些开孔的存在会破坏板壳结构的完整性，降低临近区域结构的强度，同时可能在孔缘产生局部应力集中。

目前，在结构领域应用最广泛的数值模拟方法为有限元法。在处理开孔问题时，由于有限元单元必须与开孔区域较为复杂的几何构型相适应，在网格尺寸较大时，可能存在形态较差的单元，使计算精度受到影响。同时,由于有限元网格收敛速度较慢，为了提高求解精度，将显著增大前处理的工作量和总计算量。这一矛盾体现了有限元方法在分析此类结构时的固有缺陷。

数值流形方法NMM(Numerical Manifold Me -thod)是一种较为新颖的数值模拟方法，由石根华[1]首次提出，也称为有限覆盖法FCM(Finite Cover Method)[2]，该方法通过两套独立的覆盖系统构造原问题的近似解，能够统一求解连续和非连续问题[3]，且具有良好的计算效率和精度[4]。自提出以来，数值流形方法主要应用于岩土工程领域裂纹[5-7]、大变形[8]和块体运动[9,10]等问题的求解，近年来也逐渐开始应用于结构分析[11]、流体[12]和热传导[13]等其他领域，但总体而言，该方法在各类结构分析中应用仍相对较少。

目前，已有部分有关数值流形方法的研究涉及平面圆孔算例[14]，但考虑的圆孔尺寸和载荷条件种类均较少，且未提出针对开孔的特殊流形单元，也未与有限元法计算结果进行详细对比。本文基于数值流形方法理论框架和平面圆孔问题理论解[15]，构造一种适用于平面圆孔问题的特殊孔缘单元，从而将数值流形方法应用于该类问题的求解。

2 数值流形方法基本原理

数值流形方法通过数学覆盖(Mathematical Cover)和物理覆盖(Physical Cover)这两套独立的覆盖系统实现近似解的构造和积分区域的划分。其中，自行定义的数学覆盖将求解域划分为若干数学片(Mathematical Patch)，而求解域内的边界、裂纹和交界面等将数学片进行再次剖分，得到相应的物理片(Physical Patch)，物理片的集合即为物理覆盖。物理片的重叠区域构成数值流形方法的基本单元，称为流形单元(Manifold Element)。

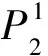
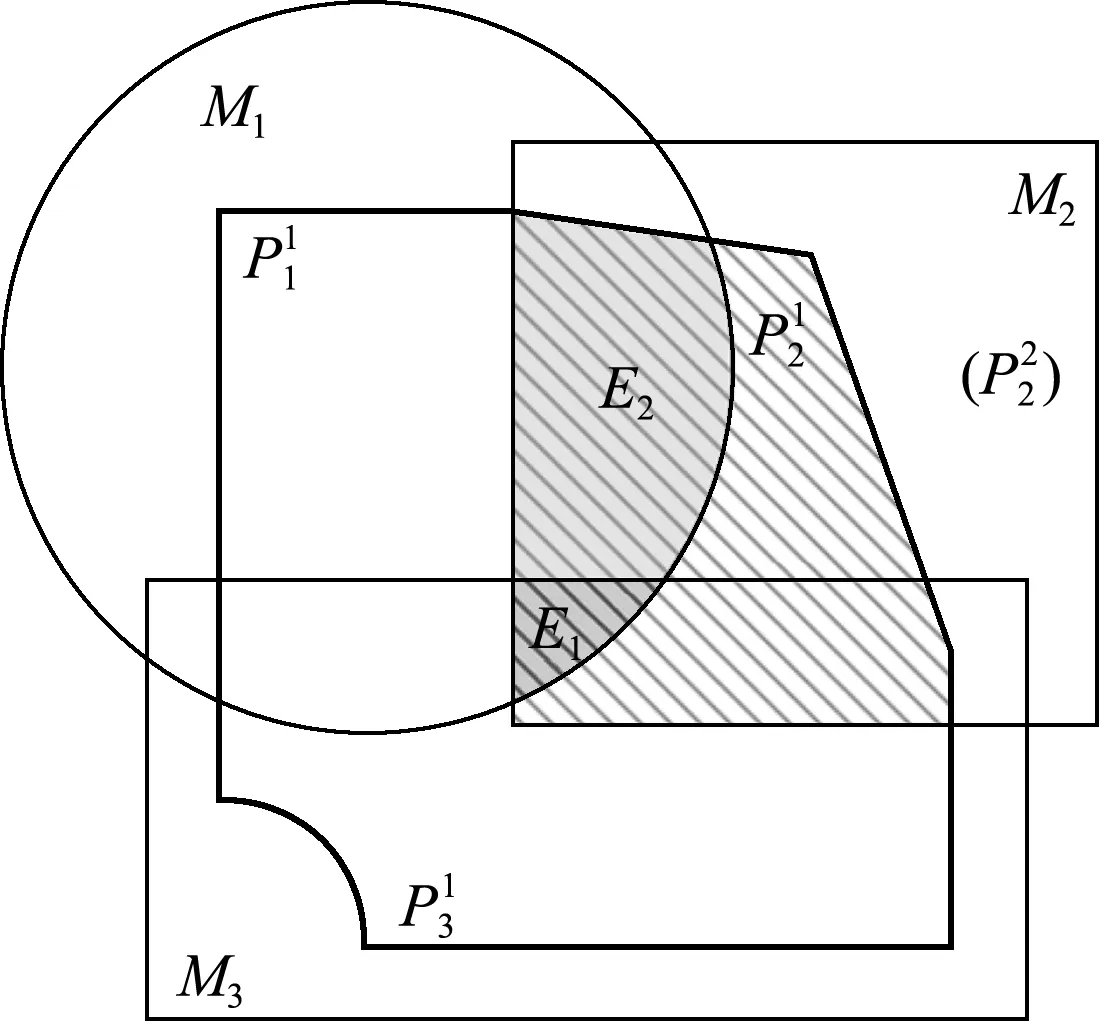
图1 数值流形方法覆盖系统

由于数学覆盖的划分具有任意性，本文采用标准网格数学覆盖，其形式如图2所示。在标准网格中，每一个顶点均张成一个矩形数学片，每个流形单元均是四个不同物理片的重合区域，如流形单元E1为P1，P2，P4和P5的重合区域。

图2 标准网格下数值流形方法的覆盖系统

在NMM覆盖系统中，每一个物理片具有各自独立的局部逼近(Local Approximation)；各个物理片的局部逼近通过权函数共同构成完整求解域的整体逼近(Global Approximation)。物理片Pi的局部逼近是一个定义在Pi上的函数空间，函数空间的基为一给定的基向量Bi(x,y)。平面问题中，物理片Pi的局部逼近记为ui(x,y)，可由基向量中的分量函数张成，即

(1)

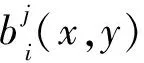
每个物理片Pi均具有对应的权函数wi(x,y)。数值流形方法属单位分解 PU(Partition of Unity) 类数值算法，其权函数需满足以下基本要求，

wi(x,y)≥0 [(x,y)∈Pi]

(2)

wi(x,y)=0 [(x,y)∉Pi]

(3)

(4)

式中Ω为求解域，n为物理片总数。在实际应用中，权函数常基于有限元单元形函数构造。由此，平面问题数值流形方法的整体逼近表达为

(5)

获得了问题域的整体逼近后，即可根据弹性力学相关理论，结合平衡方程、几何方程和本构方程，利用整体逼近推导应力和应变，随后依据最小势能原理建立系统的控制方程，并引入边界条件，该过程与有限元方法基本一致。

3 平面圆孔特殊孔缘单元的构造

3.1 孔缘局部逼近的构造

相较于有限元法，数值流形方法的优越性还体现在可以根据实际问题，选择合适形式的基构成局部逼近，显著提高求解的准确性和收敛速度。局部逼近的基可取为常数、多项式基或其他级数的基，基的维数决定了该局部逼近的自由度数。对于一般的平面问题，采用常数基张成的局部逼近即可取得较好的计算精度，此时物理片自由度数为2，可将式(1)以矩阵形式表达为

(6)

对于平面开孔问题，孔缘区域在外力作用下可能产生应力集中，应力变化较为剧烈，采用上述形式的局部逼近计算效果不好，与有限元法相比也没有明显优势，因此为提高计算精度，有必要对局部逼近的基向量进行扩展。

对于如图3所示平板边界两对边分别承受均布载荷q1和q2的情况，根据现有弹性力学解答[15]，由叠加原理可得极坐标系下圆孔附近区域应力场解答如式(7～9)。

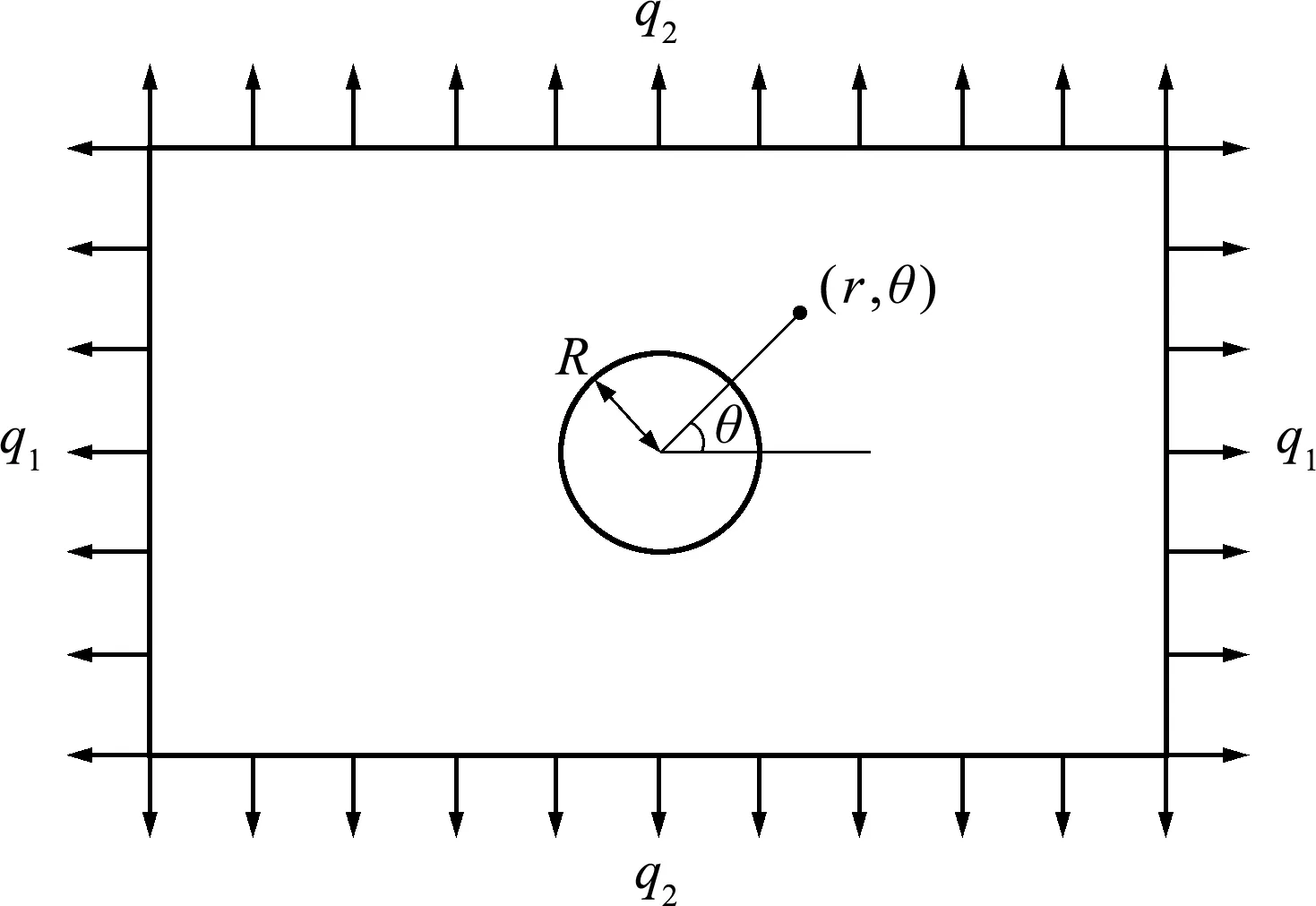
图3 四边受载的带圆孔矩形平板

(7)

(8)

(9)

式中σr为径向应力，σθ为切向或环向应力，τr θ为剪切应力，R为圆孔半径。

理论上，根据坐标转换关系可以进行应力分量转换，随后结合弹性力学物理方程和几何方程，可导出上述圆孔问题的位移解。然而，该过程非常繁琐，且上述解答是特定载荷条件下的解答，与实际情况常有出入。考虑到局部逼近更重要的是能反映位移收敛特点，且基向量增加项数不宜过多，因此在构造基向量时无需推导出精确的位移表达式，只需确定能够反映位移特点的若干项即可。

由此，本文取[1,x,y,cosθ,sinθ]为基向量，并按式(10)的形式构造孔缘区域局部逼近。

(10)

式中Hi为由基向量Bi(x,y)与二阶单位矩阵构造的基矩阵，如式(11，12)所示。

(11)

(12)

式(10～12)的(x,y)为以圆孔中心为原点的直角坐标值。di为自由度向量，每一个特殊局部逼近的自由度数为10。

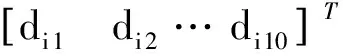
(13)

3.2 流形单元类型的划分

孔缘特殊物理片的基向量项数增加，增加了求解计算量。考虑到应力集中是一种局部效应，仅需对孔缘附近的少数物理片进行扩展，对于距离孔缘较远的流形单元，则按照一般平面问题进行处理。

本文依据单元包含的物理片类型，将问题域中的流形单元划分为三类,(1) 孔缘单元,构成单元的四个物理片均为孔缘特殊物理片； (2) 过渡单元,构成单元的物理片中有1～3个特殊物理片； (3) 常规单元，构成单元的物理片全部为普通物理片。三类单元的分布情况如图4所示，图中圆点为张成特殊物理片的顶点。

图4 三类流形单元的划分

3.3 权函数的构造

标准网格下，各数学片的权函数可按式(14,15)的形式，取为包含于该数学片的正方形网格在张成该数学片顶点处的有限元形函数构成的分块函数。

(14)

(15)

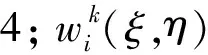
至此，将式(14,10)代入式(5)，即可得到问题域上的总体逼近，具体表达为

(16)

式中Ni由权函数及基矩阵得到，其作用类似于有限元法的形函数矩阵

因此有

u=Nd=[N1N2…Nn][d1d2…dn]T

(17)

式(17)即为总体逼近的具体表达式。

3.4 数值流形方法计算流程

通过局部逼近和权函数，由式(5)可以得到求解域的整体逼近，随后即可依据最小势能原理构建控制方程。由于数值流形方法覆盖系统中，数学覆盖与问题域边界并不保持一致，本文采用罚函数法将位移边界条件引入势能表达式，故平面问题下系统的势能如式(18)所示。

(18)

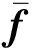
(19)

σ=Dε

(20)

式中D为平面应力问题的弹性矩阵。将式(17)代入式(19,20)，依次得到

ε=LNd=Bd,σ=DBd=Sd

(21)

式中B为应变矩阵，S为应力矩阵，其物理意义均与有限元法中的应变和应力矩阵相似。将式(21)代入式(18)，随后由∂ΠP=0即可得到控制方程，其形式可表示为

Kd=q

(22)

式中K为总体刚度矩阵，q为总体载荷列阵，分别由流形单元的单元刚度矩阵Ke和单元载荷列阵qe按编号顺序组装而成，其中

(23)

(24)

式中上标e为B或N对应当前流形单元的部分。式(23，24)的积分运算可通过数值积分实现，但在局部逼近存在非多项式的基时，需要适当增加积分点数以保证计算精度。

将单元刚度矩阵组装后求解方程式(22)，即可得到各局部逼近的精确表达式，进而得到问题域上的整体逼近。

4 算例验证

根据上述理论编制计算程序，针对承受三种不同载荷的带圆孔正方形板进行了分析。圆孔位于板的中心，半径取为R=2 m。算例1和算例3中板的边长为2a，算例2中板的对角线长为2a，均取a=10 m。板厚t=0.01 m，弹性模量E=2.1×1011MPa，泊松比μ=0.3。各算例采用数值流形方法和有限元法求解，得到不同网格精度下的解答，并进行对比。

4.1 单向受拉的带圆孔矩形板

由于该算例的载荷分布具有对称性，可取板的1/4进行分析计算，如图5所示。图中AE和BC边施加对称位移约束。取均布载荷q=100 MPa。采用n×n标准网格的数值流形方法计算结果与网格尺寸为a/n、由前处理软件自动生成的有限元计算结果进行对比，如图6所示，并取n=2,4,6,…,20。取n=80的有限元计算结果作为近似精确解。本算例中孔半径与板边长之比为1/5，达到弹性力学理论中视为无限大板的判断标准，但实际计算表明，此时点A和点B处的切向应力略大于基于带圆孔无限大板理想模型求得的解析解。

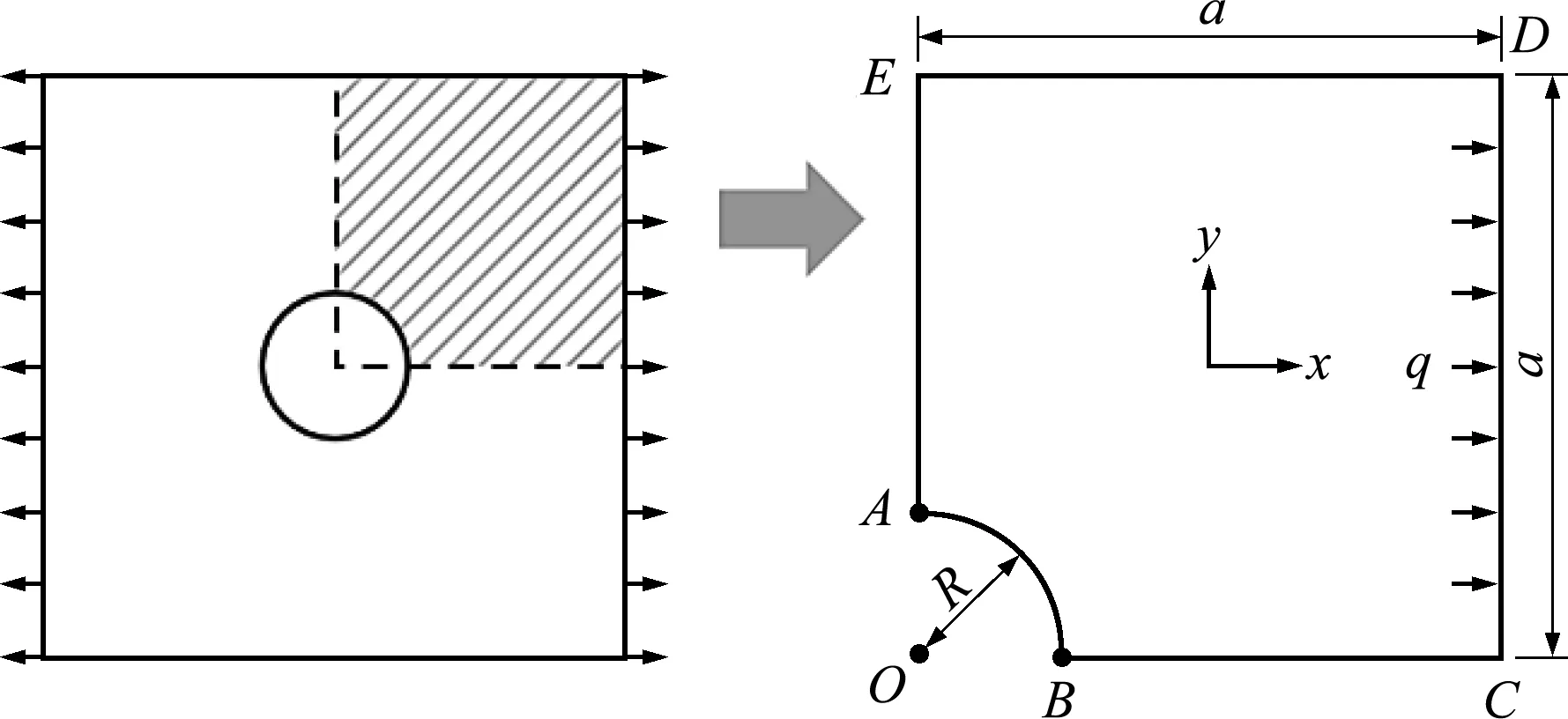
图5 单向受拉的带圆孔矩形板算例

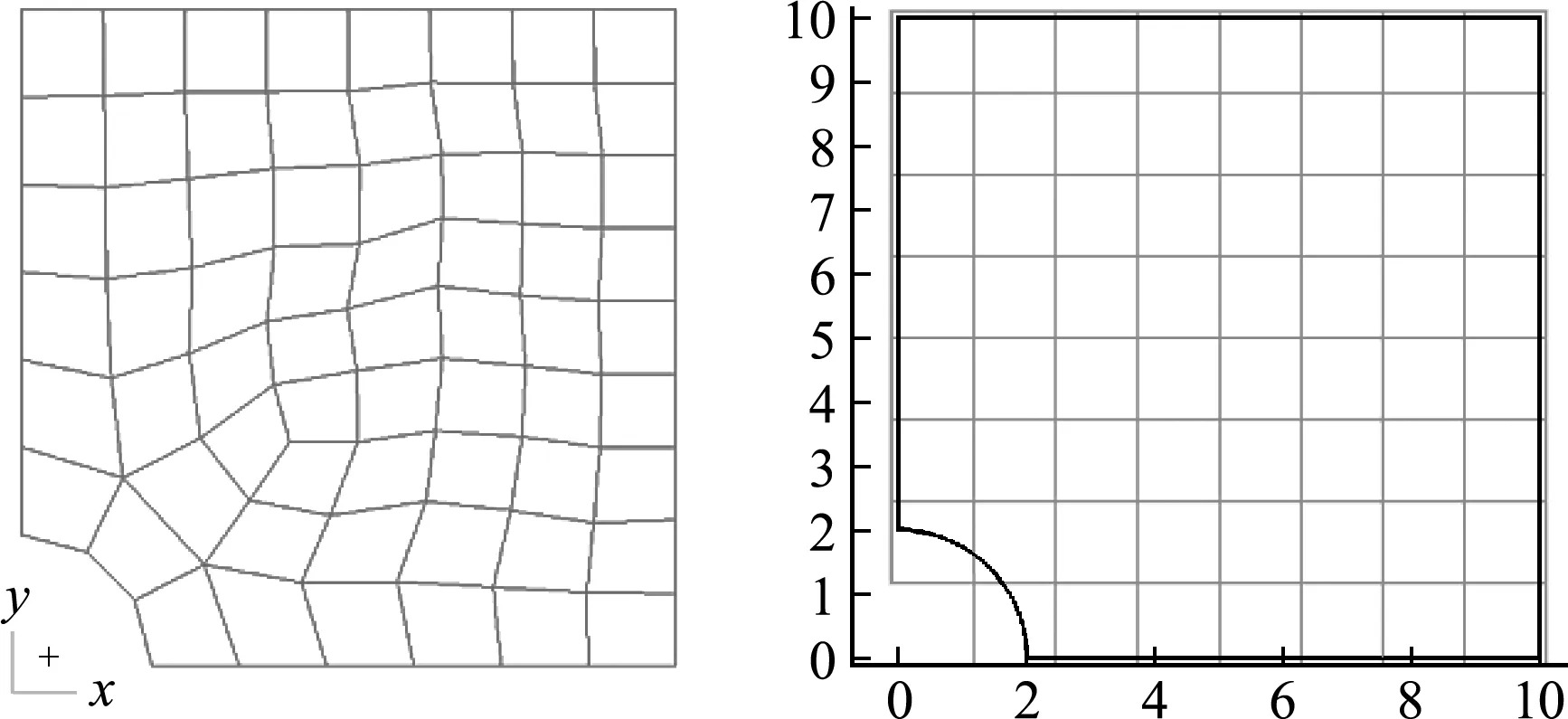
图6 有限元网格和数值流形网格(n =8)

图7给出了n=8时，数值流形方法与精密网格有限元法计算得到的Von Mises应力云图；图8给出了点A和点B处切向应力随网格密度变化的对比。可以看出，引入孔缘特殊单元的数值流形方法在网格密度较低时已经能够获得较准确的计算结果，其计算精度显著高于同等网格尺寸下的有限元法，且计算结果的收敛速度也有明显优势。但数值流形方法的计算结果并不具备有限元法的下限性，其收敛方向也不是单一的。

图7 Von Mises应力云图对比(单位:Pa)

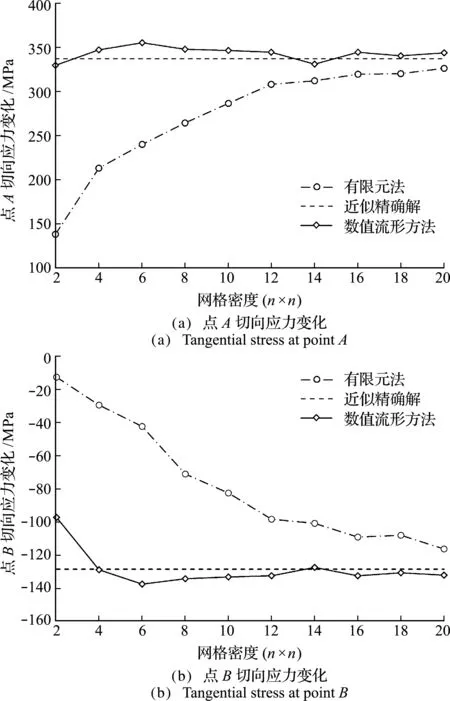
图8 点A和点B切向应力随网格密度变化(算例1)

4.2 四边受剪的带圆孔矩形板

本算例中板四边均受等大、均布的剪切载荷q作用，取其1/4进行分析计算，如图9所示。图中边AD和边BC施加对称位移约束，q=141 MPa，n=2,4,6,…,20。仍以n=80的有限元结果作为近似精确解。图10给出了特征点切向应力随网格密度变化，可以看出数值流形方法仍然具有更高的计算精度和收敛速度。

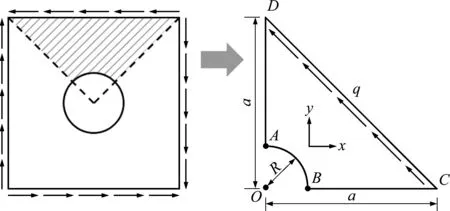
图9 四边受剪的带圆孔矩形板算例

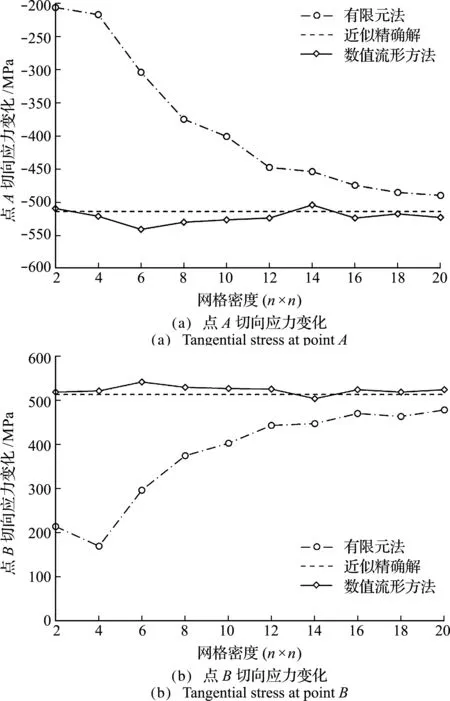
图10 点A和点B切向应力随网格密度变化(算例2)

4.3 一对边受线性分布载荷的带圆孔矩形板

本算例中板的一对边受等大和反向的三角形分布载荷，另有一边固定。如图11所示，取板的1/2进行分析计算，边CD为固定边，边AF和边BC施加对称位移约束。三角形线性分布载荷在点E处载荷值为0，点D处载荷值为200 MPa。网格数量按n×2n的方式定义，其中n=2,4,6,…,12，取n=50对应网格尺寸的有限元计算结果作为近似精确解。图12给出了特征点切向应力随网格密度的变化，可以看出数值流形方法同样具有更高的计算精度和收敛速度。

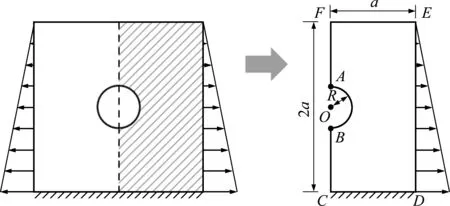
图11 线性分布载荷带圆孔矩形板算例

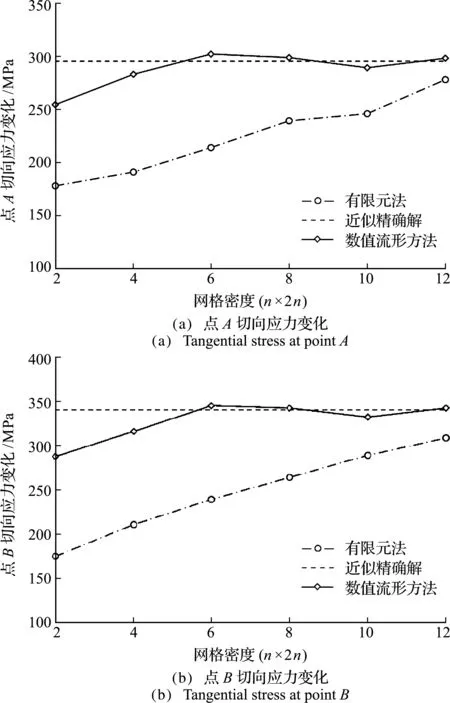
图12 点A和点B切向应力随网格密度变化(算例3)

5 结 语

本文针对有限元法在处理典型开孔结构时的不足之处，基于数值流形方法的基本框架，提出了一种适用于求解该类问题的孔缘单元，这种流形单元具有特殊局部逼近。实际计算表明，在网格密度较低的情况下，采用特殊孔缘单元的数值流形方法的计算精度相较于有限元法具有明显优势，且收敛速度更快。

数值流形方法是一种较为新颖的数值模拟方法，目前在结构领域应用相对较少。由于数值流形方法理论仍在不断完善，也未有大型通用计算软件，因此处理复杂问题仍然有一定困难，但其灵活性强、前处理工作量小以及计算精度高等突出优点均为这种方法带来了非常广阔的工程应用前景。

致谢:本文研究开展过程中得到了郑宏教授的指导和帮助，特此致谢。