基于Nitsche方法与拟牛顿求解的二维接触问题等几何分析

胡清元， 沈莞蔷， 蒋芳芳

(江南大学 理学院，无锡 214122)

1 引 言

接触问题是工业工程中常见的一类力学问题[1]。在接触问题分析方法中，解析方法精度高但适用范围受限。有限元方法适用范围广，但采用的近似网格为接触边界带来严重离散误差，迭代产生的单元畸变可能导致迭代难以收敛。等几何分析[2]方法采用非均匀有理B样条(NURBS)为基函数建模，可精确地描述结构边界，适合分析接触问题。

然而，当前等几何接触分析常见方法存在一定不足。等几何罚函数法[3]采用类似弹簧刚度的罚系数支撑接触面，但问题求解受系数取值影响很大。等几何分析中广泛采用的Mortar方法[4]通过增加虚拟公共边界施加接触条件，该方法将接触面虚拟自由度增加到系统总自由度中，因此总自由度数随着接触面演化而不断变化。此外，等几何配点法[5]也用于接触问题分析。半解析方法[6]将基本解与快速数值求解相结合，具有速度快和计算精度高的特点，在等几何分析中的应用有待进一步发展。

近年来，基于Nitsche方法的等几何分析受到持续关注。Nitsche方法最早用于有限元位移边界条件的施加[7]，之后应用到域分解问题[8]和接触问题[9]，以及后续的摩擦大变形接触问题[10]。Apostolatos等[11]综合对比了多种域分解方法的数值性能，结果表明Nitsche方法的综合表现最为稳定。Hu等[12]首次采用Nitsche方法还原接触边界条件，该列式的优势是不增加系统自由度，且有完备的数学理论支撑[9]。然而，标准的Nitsche列式需指定罚系数，该系数通常通过求解界面上的广义特征值问题得到。但对于接触问题，接触面随着迭代不断变化，若需在每个迭代步前都求解广义特征值问题，将大幅度增加计算量。

在方程求解方面，由于接触问题的强非线性，一般采用的Newton-Raphson方法需要对列式进行线性化处理，推导切线刚度阵，并在每一步迭代中对大规模矩阵求逆。这不仅需要繁杂的推导，也加重了迭代计算量。实际上，拟牛顿方法也可用于非线性问题的求解，其核心在于采用了近似的切线刚度阵，并可采取BFGS逆更新格式以避免矩阵求逆。Matthies等[13]结合拟牛顿格式与步长搜索，计算了材料和几何非线性问题。Laursen等[14]进一步采用拟牛顿方法求解接触问题，为了保证收敛，当迭代不稳定时需计算切线刚度阵。Gabriel等[15]将第一次迭代求得的解作为第二次迭代的初始近似解。然而，Nitsche方法直接将所有可能产生接触的界面纳入其接触列式，接触面的更新会直接反映在Nitsche接触列式当中。因此，如何在接触面剧烈演化和拟牛顿迭代不稳定时进行简单有效地修正，是有待进一步研究的问题。

2 等几何接触问题

2.1 等几何分析简述

等几何分析本质上是采用NURBS为形函数的等参有限元方法，采用如下方式建模几何场，

(1)

(2)

式中uA为控制点位移自由度。

由虚位移原理，得有限元弱形式

a(u,v)=l(v)

(3)

式中a(u,v)为双线性项，l(v)为线性项。为了便于推导，式(3)忽略了位移边界条件。

2.2 接触问题与接触条件

不失一般性，考虑两弹性体Ω1与Ω2发生接触，定义接触面分别为Γ1和Γ2。假定Γ1上点x1与Γ2上点x2发生接触，定义接触面外法向单位矢量为

(4)

定义接触间隙函数

g(u)=(x2-x1)·n1-[[u]]n

(5)

式中(x2-x1)·n1表示当前接触间隙，在小变形问题中认为其保持不变，[[u]]n=(u1-u2)·n1表示两点间的相对位移。

将接触面记作Γ，接触条件可写为

(6)

式中σn为其在n1方向上的分量。接触条件1表示接触面不能相互穿透，接触条件2表示接触力方向为将接触面向外推，接触条件3为互补条件。由于考虑的是无摩擦接触，故令切向应力σt=0。

3 基于Nitsche方法的接触列式

3.1 Nitsche方法简述

Nitsche方法的核心思想是将边界条件以功的形式引入有限元弱形式，其列式为

a(u,v)-Nitsche =l(v)

(7)

式中Nitsche部分通常可表示为边界积分的形式

(8)

式中f(σ)和f(v)分别为关于面力和位移的函数，具体取法取决于施加的边界条件类型。

3.2 Nitsche接触列式

从Nitsche统一列式[12]出发，接触列式可写为

(9)

式中Γ为所有可能产生接触的界面，[b]R-为标量b在R-上的投影

(10)

此外，γ为罚系数，在文献[16,17]的基础上，本文采用经验公式(11)，

(11)

式中E为杨氏模量，p为形函数阶次，d为问题维度，h1和h2表示接触面两侧的网格尺寸。

在可能的接触面Γ上，Nitsche列式通过投影算子判断积分点上的函数值来还原接触条件[9]。

(1) 当接触未发生即g>0时，接触条件3要求σn=0，此时[σn+γg]R-=0。

(2) 当接触发生即g=0时，接触条件2要求σn≤0，此时[σn+γg]R-=σn。

(3) 当g<0时，违背接触条件1，通过大数γ将接触反力放大，从而将接触面弹回。

Nitsche接触列式的物理意义是利用接触力在虚位移v上做的虚功修正有限元弱形式。其中，接触力主要为接触面Γ上面力σn，以及当接触面发生穿透时接触间隙g通过罚系数γ所得接触反力。

4 拟牛顿迭代求解格式

4.1 拟牛顿方法与BFGS逆更新公式

接触问题为强非线性问题，接触问题非线性列式的Newton-Raphson迭代求解格式为

KT(ui)·Δui + 1=R(ui)

(12)

式中KT为切线刚度阵，通常需要通过对列式进行线性化处理得到；余量计算方式为

R(ui)=l(v)-a(ui,v)+

(13)

Newton-Raphson迭代格式需要进行线性化推导，更重要的是，每次迭代都需要求解切线刚度阵的逆

(14)

这严重增加了计算量和分析时间。

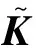
(15)

并通过BFGS公式直接更新矩阵的逆，

(16)

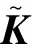
4.2 迭代初始化与接触修正

(17)

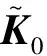
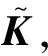
(18)

其中

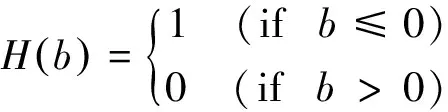
(19)

具体修正策略为,在一定迭代次数(本文设置为8次)后，当本次余量范数大于前一次时，认为接触面演化较为剧烈，BFGS的自修正特性不足以及时反映接触面变化，此时需将BFGS的迭代内核替换为式(18)所得割线刚度阵，从而保证加速收敛。

5 算 例

5.1 Taylor接触

Taylor接触算例[18]是接触问题的分片实验，该算例重点关注非协调网格能否均匀地传递接触压力，用于检验接触列式的正确性。如图1所示，两物体杨氏模量E=109Pa，泊松比υ=0.3，上方物体受均布压力f=108N/m2，两模型网格划分不同。算例解析解为

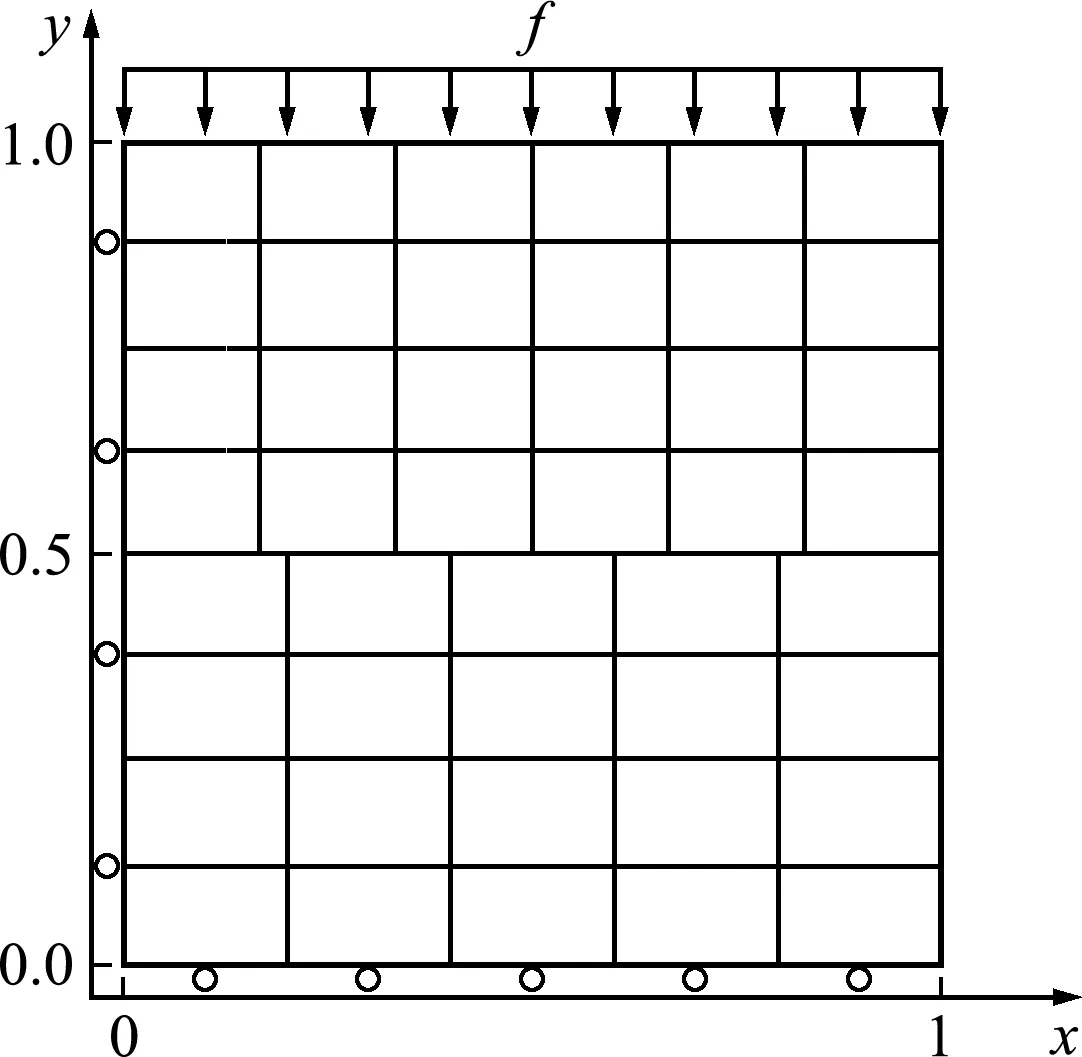
图1 Taylor接触算例

ux=0.03xm,uy=-0.1ym

σx x=0 Pa,σy y=-100 Pa,σx y=0 Pa

接触迭代记录列入表1，经过6次拟牛顿迭代后系统收敛。采用本文列式计算所得位移uy结果如图2所示，结果表明,列式可以得到正确的位移响应。应力σy y的相对误差如图3所示，最大误差为0.13%。需要说明的是，Nitsche方法采用积分的形式将边界条件弱施加在系统中，对接触问题，接触力通过高斯积分点传递，因此无法严格地通过Taylor接触实验。但随着网格加密，误差减小，本文列式可以弱通过Taylor接触实验。

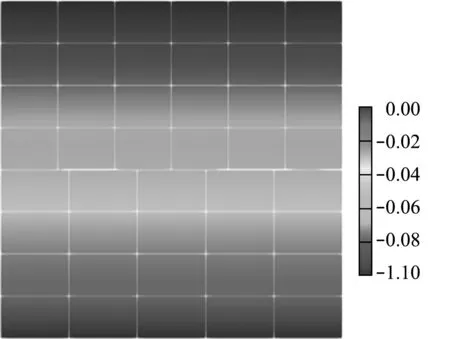
图2 位移云图

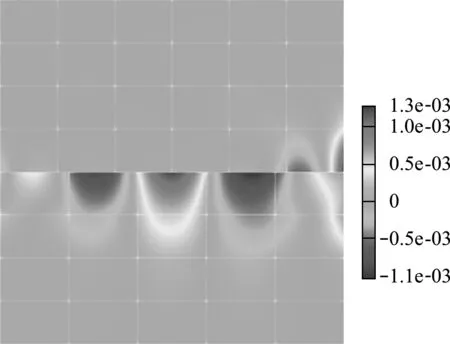
图3 应力相对误差

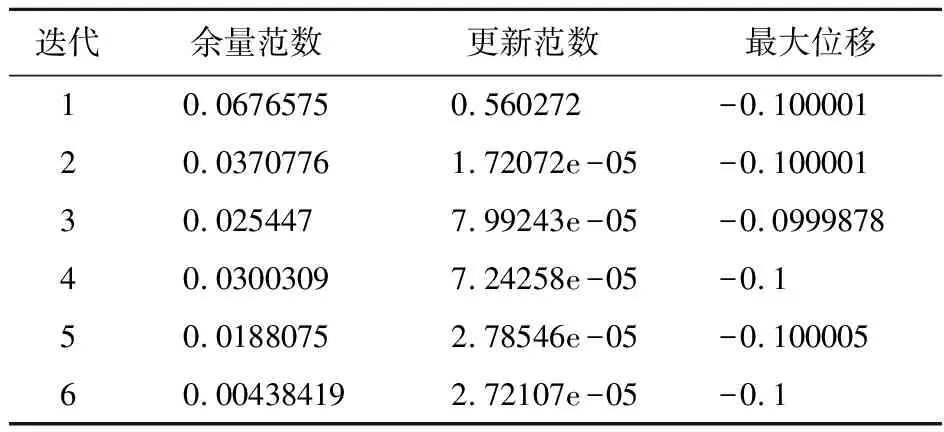
表1 Taylor接触迭代记录

5.2 Hertz接触

Hertz接触算例是接触问题中的经典点接触算例，原问题要求两个杨氏模量不同和半径不同的三维圆柱体接触。本算例将原问题退化，考虑一个二维弹性圆面和刚性平台(即弹性模量和半径均为无穷大)的接触问题。如图4所示，上方圆面弹性模量E=0.02×109Pa，泊松比ν=0.1，半径r=0.2 m，承受体力gz=-1.3×106N/m3。本算例理论解为[19]，接触力压力为2.2918×106Pa，半接触面宽度为0.0454 m。

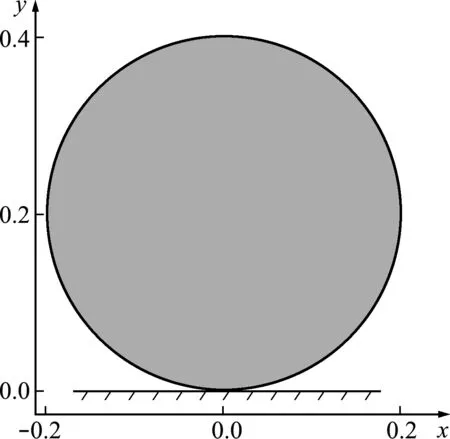
图4 Hertz接触算例

采用8×8网格计算该算例，接触迭代记录列入表2，其中在第13次迭代时采用了割线刚度阵修正，修正后的余量范数大幅度降低，加速了收敛过程。计算所得竖向位移uy云图如图5所示，结果表明下方刚体可以有效地支撑上方弹性体，二者之间产生一段平直的接触面。在不同网格划分下计算所得接触面宽度与接触应力如图6所示，其中黑色实线为理论解，结果表明随着网格加密，本文列式可以得到较为精确的解答。

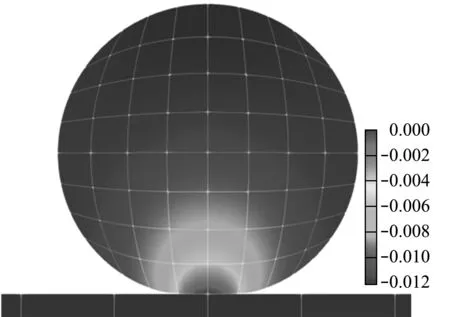
图5 位移云图

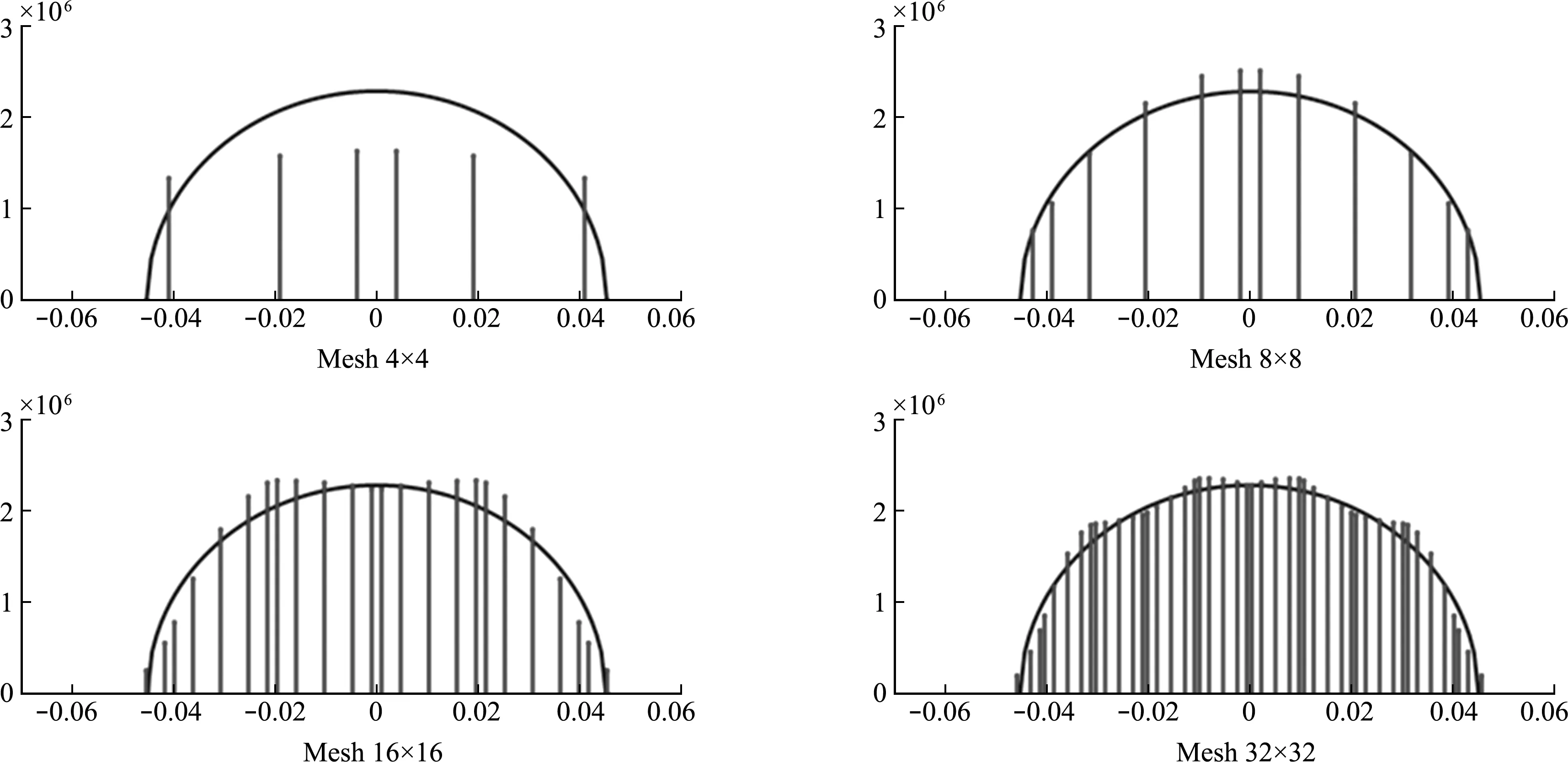
图6 不同网格下接触面宽度与接触应力

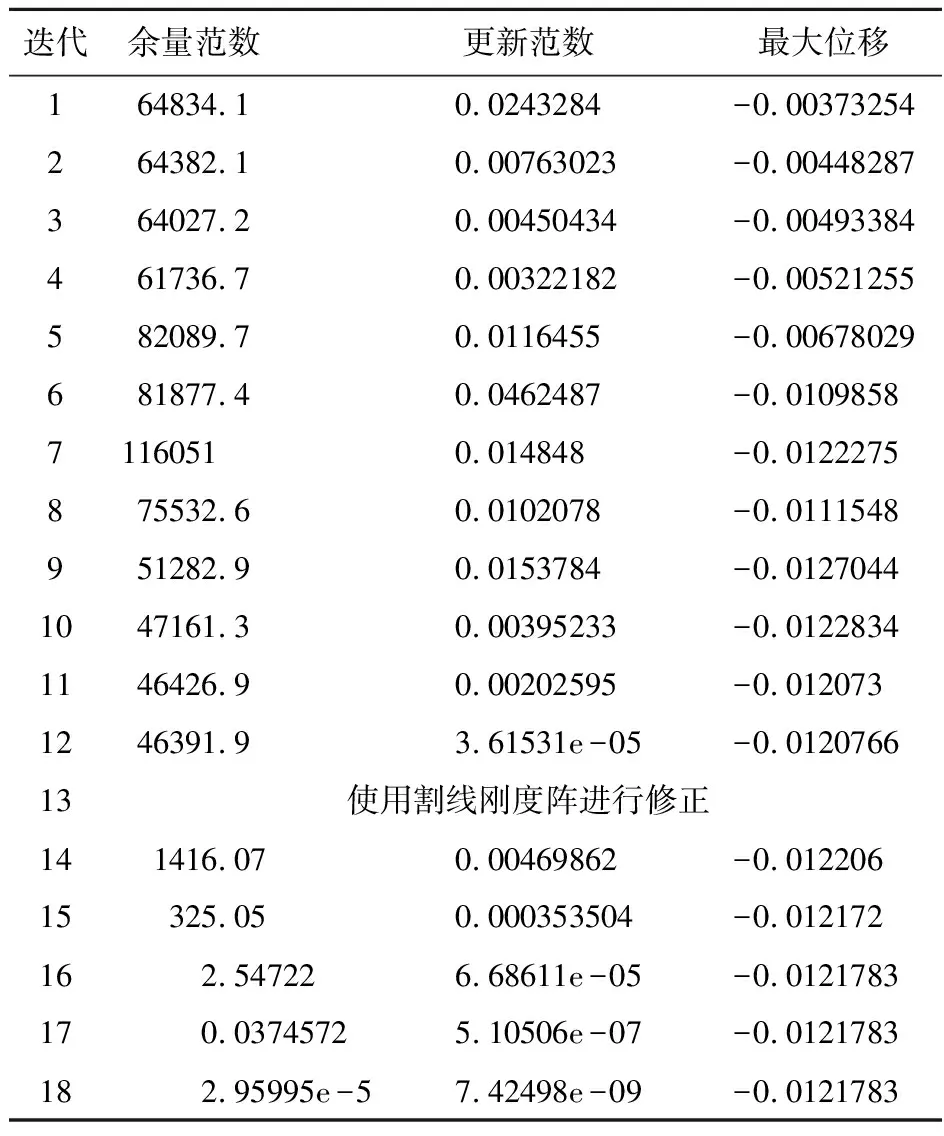
表2 Hertz接触迭代记录

仍采用8×8网格，使用单线程计算对比。等几何方法计算总耗时323 s，接触应力最大误差 9.91%；使用同样的网格划分，有限元计算总耗时213 s，接触应力最大误差28.7%。传统有限元基函数构造简单，而等几何分析中的基函数需递推计算，因此等几何分析耗时较长。但值得指出的是，有限元前处理时划分网格的时间并没有统计在内，而等几何分析直接采用几何模型计算。并且，在本算例中等几何方法仅用较为粗糙的网格即可精确描述接触边界，迭代过程稳定，最终得到较精确的结果，而这在传统有限元中是难以做到的。

本算例的接触表面是光滑的，对粗糙表面的接触问题，其接触表面为折线状。因为无法体现等几何方法描述曲线边界时的精度优势，此时的等几何方法作为一种高阶有限元方法，其计算精度应略优于传统有限元。

6 结 论

本文在等几何分析框架内，基于Nitsche方法推导了二维小变形无摩擦接触问题列式。非线性列式采用拟牛顿迭代格式求解，由BFGS公式直接更新近似切线刚度阵的逆。本文给出了一个Nitsche列式中罚系数经验公式，提出了基于Nitsche界面耦合列式的拟牛顿迭代初始化方法，并采用割线刚度阵解决由接触面变化导致的BFGS更新能力不足问题。

所提出的接触分析方法具有较强的适用性，在粗糙网格下依然可以精确描述接触边界，列式推导简单，计算量小。算例表明，基于Nitsche方法的接触列式以积分形式近似地施加接触条件，基于拟牛顿方法和割线刚度阵修正的迭代过程能够较好收敛，最终可以得到较精确的接触面宽度和接触面压力解答。