剪切和扭转工况下微纳米薄壁蜂窝的等效剪切模量计算
2021-11-02刘海洋
贺 丹, 刘海洋
(1.沈阳航空航天大学 辽宁省飞行器复合材料结构分析与仿真重点实验室,沈阳 110136;2.西安交通大学 机械结构强度与振动国家重点实验室,西安 710049)
1 引 言
微尺寸蜂窝[1]在微机电系统(MEMS)中具有显著的应用优势,可用于制备微型电极[2]、微型能量存储和转换设备[3]、微传感器[4]和超级电容[5]等。为保证构件满足强度、刚度、耐久性和可靠性等指标,对蜂窝的力学性能进行预测十分必要。
Gibson等[6]基于梁理论,给出了一种蜂窝芯层面内和面外等效模量简便的计算方法,但在推导过程中并未考虑壁板伸缩变形对面内刚度的影响,导致了蜂窝芯层材料弹性刚度矩阵奇异[7]。富明慧等[7,8]将此影响加以考虑,对Gibson的结论作出修正,克服了刚度矩阵奇异的缺陷。Becker[9,10]考虑了面板对芯层的约束效应,并将蜂窝胞壁等效为薄板,以各胞壁应变场为未知量,通过能量法求解了不同芯层高度蜂窝的等效模量,发现面板的存在会使得蜂窝芯层的等效模量随芯层高度变化而改变,芯层等效模量与高度之间具有非线性函数关系,此现象称为高度效应。Li等[11,12]则认为等效模量不仅和尺寸有关,还和受力状态有关,采用三角级数来模拟蜂窝胞壁位移场,研究了蜂窝等效模量的计算方法,并讨论了等效模量与芯层高度之间的关系。
当蜂窝的壁厚处于微纳米量级时,材料的尺度效应[13-16]可能会对蜂窝的力学性能产生影响。尺度效应是指当材料的尺寸进入微纳米尺度时,其强度和刚度随材料尺寸变化而变化的现象。这种现象难以通过经典连续介质力学理论进行解释,因此研究者提出了诸如应变梯度[13]和偶应力[16-20]等理论,在这些理论的本构方程中,存在若干个和材料尺寸相关的尺度参数,从而具备了描述尺度效应的能力。Yang等[21]提出了一种修正偶应力理论,其中仅包含一个材料尺寸参数,十分便于工程应用。基于这种理论,已有大量关于微纳米板和梁结构的研究工作见诸报道[22-25]。Zhu等[26-28]基于修正偶应力理论,研究了不考虑面板约束的微尺寸六边形、三角形和正方形蜂窝芯层面内外五个独立弹性参数的计算方法。张春浩等[29]基于该理论建立了芯层Y模型,并给出了考虑尺度效应的蜂窝面内等效模量计算方法,讨论了蜂窝壁厚对其等效模量的影响,得出微尺寸蜂窝芯层等效模量将随壁厚尺寸减小而增大的结论。
综上所述,文献[6,8]未考虑高度效应、受力形式和尺度效应;Becker[9,10]未考虑受力形式和尺度效应;Li等[11,12]未考虑尺度效应;而文献[26-29]则仅考虑了尺度效应。因此,本文综合考虑蜂窝受力形式、尺度效应以及面板约束引起的高度效应,分别给出了剪切和扭转工况下的六边形微尺寸蜂窝等效剪切模量的计算过程,并讨论了蜂窝芯层高度和胞壁厚度对等效剪切模量的影响。
2 蜂窝胞壁的应变能
依据Yang等[21]提出的修正偶应力理论,三维弹性体的应变能定义为
(1)

(2)
位移矢量ui与转角矢量θi之间的关系为
(3)

(4)
式中lm为材料尺寸参数,λ和μ为Lame常数,其与弹性模量E,泊松比v之间的关系为
λ=Ev/[(1+v)(1-2v)] ,μ=E/[2(1+v)]
(5)
在推导微尺寸蜂窝等效模量的过程中,可将蜂窝各胞壁简化为微尺寸薄板,其位移场可取为[30]
u1=us(x,y)-z[∂w(x,y)/∂x]
u2=vs(x,y)-z[∂w(x,y)/∂y]
u3=w(x,y)
(6)
设板厚为t,并将式(1)应变能U拆分为由应力和应变耦合得到的U1,以及偶应力和曲率耦合得到的U2,则U=U1+U2,综合式(2~6),得到U1和U2的表达式分别为
(7)

(8)
式中D为板的弯曲刚度,εs x和εs y为中性面的拉伸应变,即
εs x=us,x,εs y=vs,y
(9)
因此,当微尺寸板的位移场〈us,vs,w〉为已知时,板的应变能便可通过式(7,8)求得。
3 微纳米薄壁蜂窝等效模型
考虑一个典型的六边形蜂窝特征单元REV[11],如图1所示,其中斜胞壁长度为L,厚度为t;直胞壁长度为h,厚度为t′=2t,斜胞壁与水平线夹角为θ,各胞壁垂直纸面方向长度为b。考虑到结构对称性,可只分析图2所示1/8 REV以简化问题。1/8 REV可视为由厚度均为t及z方向长度均为b/2的三块薄板组成,其中板EFHG和ABDC的第三方向长度为h/2,板CDFE的第三方向长度为L。

图1 蜂窝特征单元

图2 1/8蜂窝特征单元
根据能量均匀化理论,图1虚线所围均匀体的总势能应与蜂窝特征单元总势能相等,即
(10)

(11)
(12)

4 不同工况下微纳米薄壁蜂窝的等效剪切模量计算
4.1 剪切工况
假设在蜂窝面板施加面内剪切初应变γX Y,如图3所示,由于面板与蜂窝芯层为固接,且面板刚度远大于芯层,因此芯层将随面板发生剪切变形,斜胞壁将因端点水平位移不同而产生线应变εs,

图3 蜂窝REV剪切变形
(13)
变形后的结构无法满足平衡方程,因此应力将在芯层上重新分布,从而产生如图4所示的附加位移场,直至达到平衡位置。应力的重分布将极大降低蜂窝刚度,使得等效剪切模量对高度敏感[11,12]。

图4 剪切工况下1/8 REV各壁板附加位移
考虑到蜂窝芯层的边界形式和变形特点,板EFGH的附加位移函数可取为[11]
(m=2i-1)(14)
式中a0,ai和bi为待定参数,N为三角级数展开项数,理论上N需取至无穷,但实际取前10项便可保证计算精度,故本文N取10。
对于板CDFE,附加位移函数可取为[11]
us=a0(2/b)x
(15)
除附加位移场产生的线应变以外,板CDFE沿局部坐标y2的线应变εy还应包括式(13)基础应变εs,
εy=εs-∂vs/∂y
(16)
对于板ABDC,附加位移函数可选为[11]
(17)
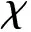
(18)
(19)

由于应力重新分布过程中外力做功为0,故系统总势能与总应变能相等,即
πint=U1+U2
(20)
根据最小势能原理,真实位移使系统总势能取极值,故系统总势能对待定参数的偏导等于0,即
(21)
4.2 扭转工况
假设在蜂窝面板施加矢量方向与面板平行的扭转切应变βX,REV会产生切应变γX Y
(22)
式中βX ′ Y=βX/(h+lsin ϑ)。板CDFE因边EF和边CD水平位移不同而产生线应变,其中边EC的线应变为
εs=(UE-UC)cosθ/L=-γX Ysinθcosθ
(23)
在局部坐标系x2-C-y2中,线应变沿x2方向线性分布[10],且在边EC取得最大值,因此有
εs(x)=-ακ(b/2-x)
(24)
式中κ=βX ′ Y为板的扭转曲率,α=sinθcosθ。
图5变形后的结构同样无法满足平衡方程,因此应力将重新分布,各胞壁将产生附加位移场,如图6所示,对于板EFHG,根据边界条件和位移形式选取的附加位移函数为[11]

图5 1/8 REV扭转变形
图6 扭转工况下1/8 REV各壁板附加位移
(25)
对于板CDFE,附加位移函数可取为[11]
(26)
考虑式(23)基础应变εs(x),板CDFE的y1方向应变应为基础应变和附加位移产生的应变之和,
(27)
对于板ABDC,附加位移函数可取为[11]
(28)
将式(25~28)代入式(2),并将得到的应变分量和曲率分量代入式(7,8),得到每块板的应变能,进而得到1/8 REV应力与应变耦合应变能U1以及偶应力与曲率耦合应变能U2,如式(29,30)所示。
(29)
(30)

5 算例分析
可以看出,剪切和扭转工况的等效剪切模量具有相同的上界,随着芯层高度b的增加,两种工况下的蜂窝等效剪切模量均表现为逐渐减小后趋于不变,即体现出高度效应现象。这是由于面板与芯层存在较强的位移耦合[9],当芯层高度较低时,耦合效应使芯层具有较大刚度,随着芯层高度增大,耦合效应逐渐减弱,当芯层高度超出一定范围时,面板对芯层的约束可以忽略不计,故等效剪切模量最终表现为不随芯层高度变化的直线。而Zhu[26]在建立模型时未将这种位移耦合加以考虑,因此所得等效剪切模量结果是不随芯层高度变化的直线,与Li经典理论结果差异较大。t取值越小,等效剪切模量随高度增加而衰减的速度越快,即蜂窝胞元尺寸较小时,其刚度对芯层高度的变化更为敏感。还可以看出,本文基于修正偶应力理论的计算结果总是大于Li基于经典理论的结果,且随着胞壁厚度的降低,二者间的差异愈发明显,即捕捉到了所谓的尺度效应。观察两种工况下等效剪切模量随芯层高度的衰减速度可发现,本文得到的等效剪切模量衰减速度小于Li的衰减速度。随着蜂窝胞壁厚度增加,尺度效应逐渐不明显,两组解之间衰减速度的差异也逐渐消失。因此,对于宏观尺度蜂窝而言,高度效应对等效模量的影响是非常显著的;而当蜂窝壁厚进入微纳米量级时,由于尺度效应的存在,芯层的刚度变强,从而降低了面板约束和高度效应对结构等效模量的影响。换言之,当尺度效应变得显著时,等效模量对芯层高度的敏感性将有所下降。比较图7和图8的衰减趋势,可以看出扭转工况时的等效剪切模量衰减速度低于剪切工况时的衰减速度,这是由于两种工况的不同应力分布方式导致的[11]。
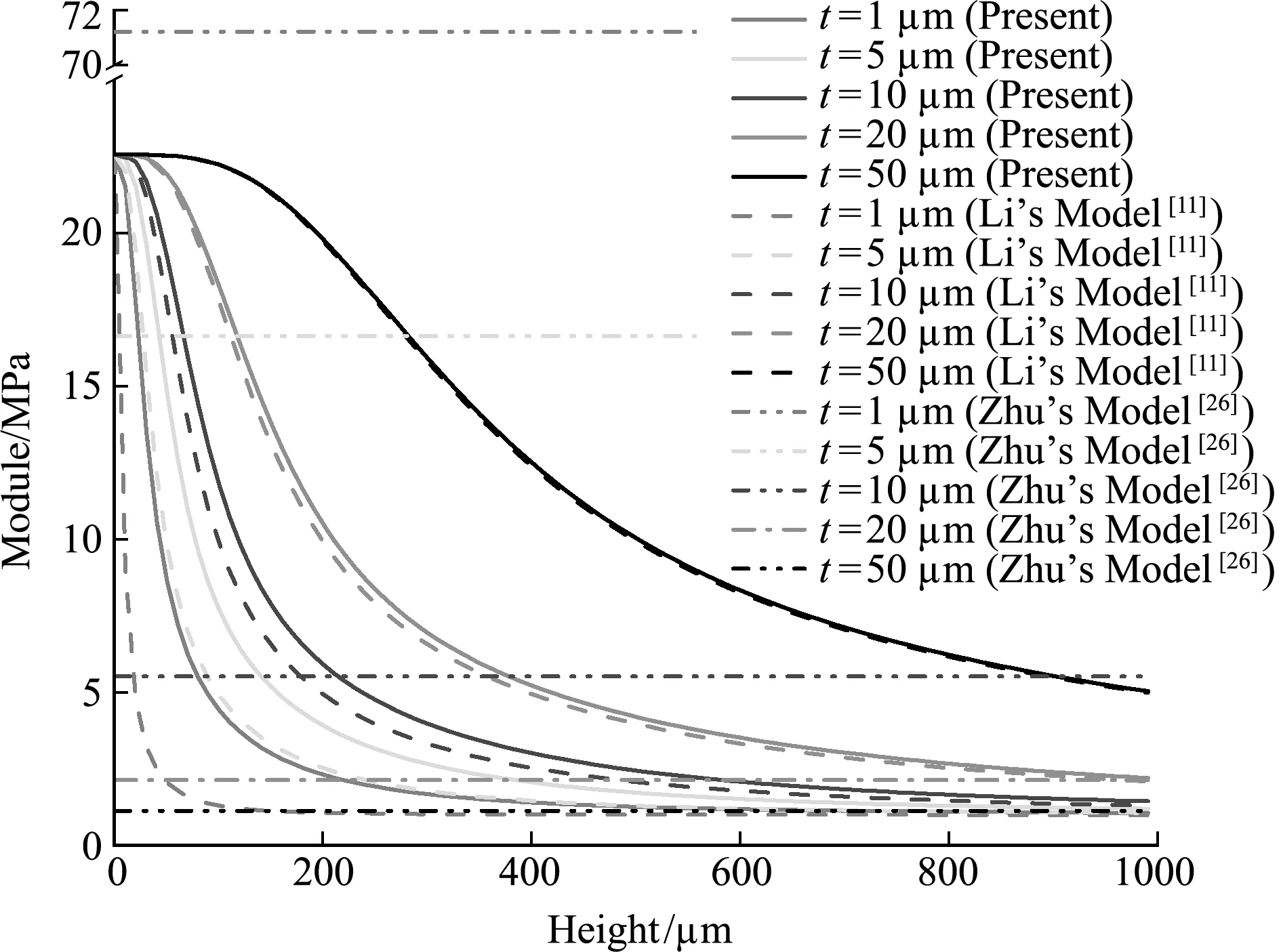
图7 剪切工况下蜂窝等效剪切模量
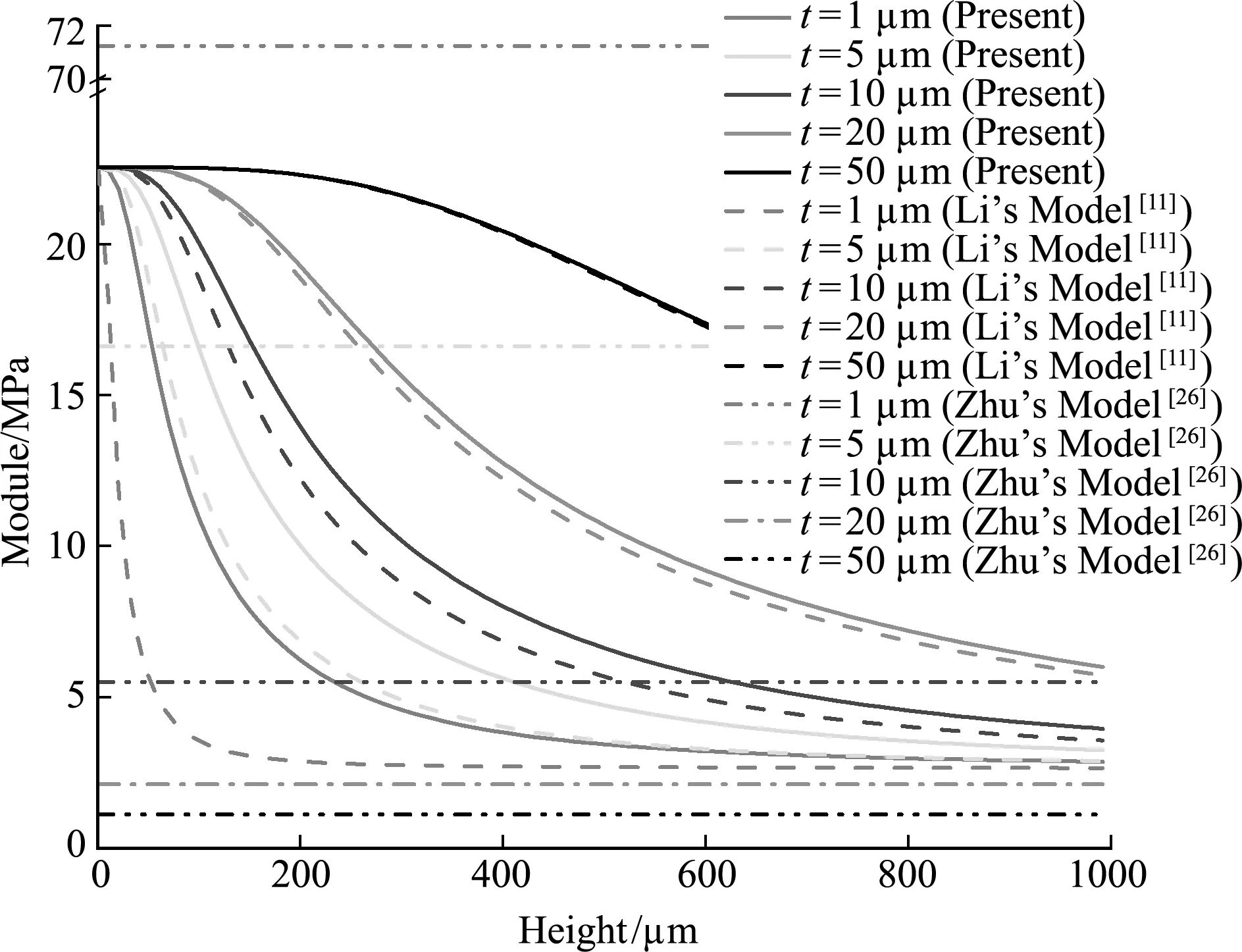
图8 扭转工况下蜂窝等效剪切模量


图9 偶应力理论与经典理论等效剪切模量比值(b =200 μm)
6 结 论
(1) 当芯层高度趋近于零时,剪切和扭转工况的等效剪切模量具有相同的上界。随着芯层高度b的增加,两种工况下的蜂窝等效剪切模量均表现为逐渐减小后趋于不变,即体现出高度效应现象。在这个过程中,扭转工况下的等效模量衰减速度低于剪切工况,最终两种工况会收敛于-不同的下界。
(2) 当蜂窝胞壁的厚度进入微纳米尺度时,本文给出的等效剪切模量总是大于经典理论的解,即描述了尺度效应。胞壁厚度越小,尺度效应越明显;而当厚度t远大于尺度参数时,尺度效应消失,此时本方法预测的模量与经典理论一致。
(3) 对于经典理论而言,蜂窝胞元尺寸越小,等效剪切模量随高度增加而衰减至最小值的速度越快。而基于修正偶应力理论所得等效剪切模量的衰减速度明显低于经典理论,即当尺度效应变得显著时,等效模量对芯层高度的敏感性将有所下降,这种现象会随胞壁厚度增大而逐渐消失。
