代理模型在机翼油箱晃动适航审定中的应用
2021-11-02王东林缪圣亮
孙 滨, 韩 松, 王东林, 李 明*, 缪圣亮
(1.中国民用航空沈阳航空器适航审定中心,沈阳 110043;2.大连理工大学 工业装备结构分析国家重点实验室,大连 116024; 3.中航通飞研究院有限公司,珠海 519040)
1 引 言
随着航空航天技术发展,液体晃动引起的飞行器结构破坏逐渐得到重视和关注[1-3]。在各类航天器飞行过程中,受不稳定气流、发动机转子失衡以及飞行轨迹和姿态的变换等诸多因素影响,液体燃料和冷却剂在储液箱内会发生剧烈晃动,导致储液箱壁面应力集中,引发壁面破坏导致燃料泄漏或爆炸,造成巨大的损失。因此,在飞行器适航审定中,考虑储油箱低频晃动引起的壁面结构破坏非常必要。
储油箱晃动涉及到多因素流固耦合,问题复杂,全尺寸试验代价高。翟冰冰等[4]通过对大型运输类飞机油箱进行适航验证,确定了晃动频率、角度和试验载液量等试验参数。李宝方[5]对晃动试验的美国军用规范进行总结,并介绍了主要试验设备和方法。叶休乃[6]对民航适航性条例和美国军用规范中有关油箱晃动和晃振试验标准进行了总结。晃动物理试验实施过程复杂,试验周期长,需要进行大批量试验来涵盖多种工况,代价较高,不能经济有效地反映出工况条件与响应间的关系,不利于飞行器的快速高效适航审定。
随着计算机和有限元的发展,数值模拟开始进入油箱晃动领域。韦杰创[7]利用任意拉格朗日-欧拉法对航空弹性薄壁油箱开展流固耦合计算,验证了有限元计算的准确性,并对不同的晃动幅值、晃动频率和载液比例进行了结果分析。李威锋[8]建立了油箱流固耦合模型,分析了影响油箱晃动的因素,并结合动力学分析给出了油箱寿命预估。张雄等[9]提出了一种新型流固耦合不可压物质点法,并研究了运动刚体容器中的液体晃动问题,解决了完全不可压物质点法无法处理不规则边界和移动边界的问题。与物理试验相比,数值模拟有效降低了经济成本,可以方便计算任意外部激励下油箱的晃动响应。但流固耦合计算复杂,单个算例需耗时若干小时,且基于离散工况的有限元无法给出外部激励与结构响应规律,难以有效应用于飞行器快速概念设计和适航审定。
响应面代理模型由Box等[10]提出,核心是在试验设计基础上建立响应值与自变量之间的显式函数来代理真实模型,对多变量非线性问题尤为适用[11-13]。文献[14,15]对响应面代理模型进行改进,不仅提高了模型精度,而且成功解决了多种复杂的工程问题,可潜在应用于复合材料燃油箱晃动分析。响应代理模型的精度和求解复杂程度依赖于样本点的选取方法,如基于拉丁方设计开展等概率分层抽样具有很好空间填充性和均衡性[16]的拉丁超立方采样法。
本文使用拉丁超立方合理布置样本点分布,基于复合材料燃油箱液体晃动有限元计算结果建立响应面代理模型,给出晃动频率、晃动幅值和载液比与油箱壁面峰值主应变间的响应面函数。通过数值模拟和物理试验进行响应面代理模型的校验。基于代理模型来预测复材油箱晃动最危工况,指导工程实际和飞机适航审定。
2 机翼油箱晃动物理试验和数值仿真
基于民航规章开展飞机机翼全尺寸复材燃油箱晃动试验。晃动试验的激励方式根据《HB 6757-1993飞机燃油箱晃动和振动试验要求》施加,使油箱能够绕晃动轴线(油箱晃动时所围绕的固定轴线)作俯仰或横滚方向晃动。试验件选取全尺寸复材飞机右机翼整体油箱,试验前对油箱进行冲压至内部压力比周围大气高10.5 kPa±0.5 kPa,并保压半小时检查其气密性,试验后排空油箱内液体,再次冲压进行气密性检查。试验夹具保证具有足够的支持刚度来模拟机翼燃油箱与机身的实际连接。根据有限元计算结果,在油箱上下蒙皮主应变较大且应变梯度较小位置贴45°直角应变花,测量壁面应变分布和峰值主应变。整个试验过程在室温大气环境下进行。各晃动试验工况参数列入表1。由于全尺寸模型晃动试验经济成本和时间代价昂贵,本文仅进行了三次物理试验用于数值仿真对比和响应面模型验证。后续工作中将适当增加试验次数增加有效实验数据。

表1 晃动试验工况
基于商用有限元软件ANSYS Workbench开展机翼复材燃油箱晃动有限元流固耦合分析。基于机型设计,将如图 1所示的机翼结构沿隔板分成六个油箱,1、2和3为主油箱,4,5和6为副油箱,分别考虑不同油箱的载液比。由于1号主油箱为研究晃动规律的重点,因此本文仅考虑1号主油箱的载液比影响。使用三维不可压雷诺时均Navier-Stokes方程(RANS方程)和标准k-ε湍流方程描述液体流动,使用流体体积法VOF(Volume of fluid)模型进行流体晃动自由液面追踪。引入SIMPLE(Semi-Implicit Method for Pressure -Linked Equation)提高流体计算收敛速度。由于液体晃动不会导致油箱壁面的大变形,因此通过单向流固耦合将液面变化导致的动态变化压力场传给固体域结构分析,最终得到机翼复材燃油箱壁面应变分布。
(1)造型前准备 流涂质量、含水率、变形量等关键项经过检测合格后的黑模,可用于造型。首先,进行垫料、填料的设计与装配,除工艺设计床身外围垫料外,在内腔必须设计填料、衬料,以防止在流砂紧实过程中受压力导致黑模变形,同时衬料要求布置合理,既能保证支撑又要能够顺利取出;另外,还需要在外侧方门设置堵头,目的是按工艺设定顺序流砂,堵住的位置在下型反转后再流砂。

图1 机翼油箱结构
3 机翼油箱晃动响应面代理模型
(1)
式中βi,βi i和βi j分别为一阶项、二阶项和交叉项的待定系数,xi为第i个自变量,n为自变量个数,本文取n=3。
样本点抽样采用拉丁超立方等概率分层采样法,最大化样本点间距和最小化相关系数,使用尽可能小的样本空间表征更多种随机可能性。在晃动频率F(15 次/min~45 次/min),晃动幅值A(5°~20°)和油箱载液比L(0.3~1)范围内进行采样,步骤如下。
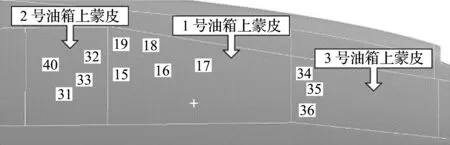
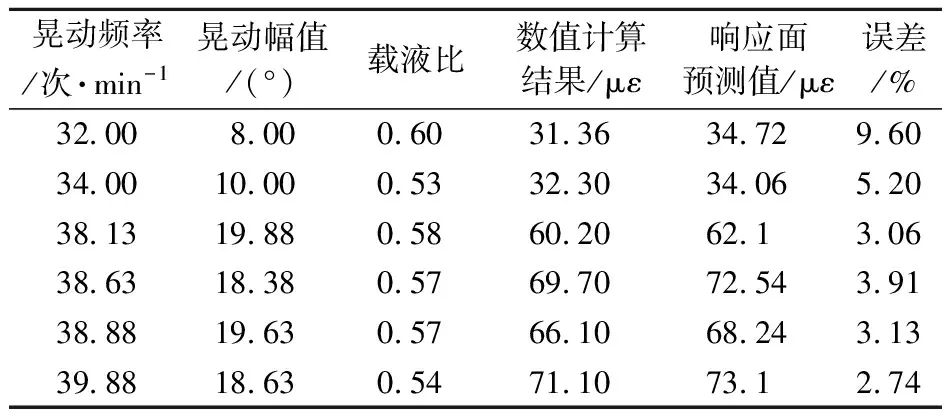
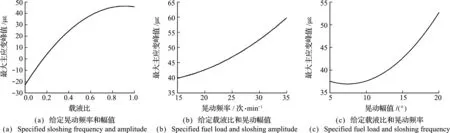
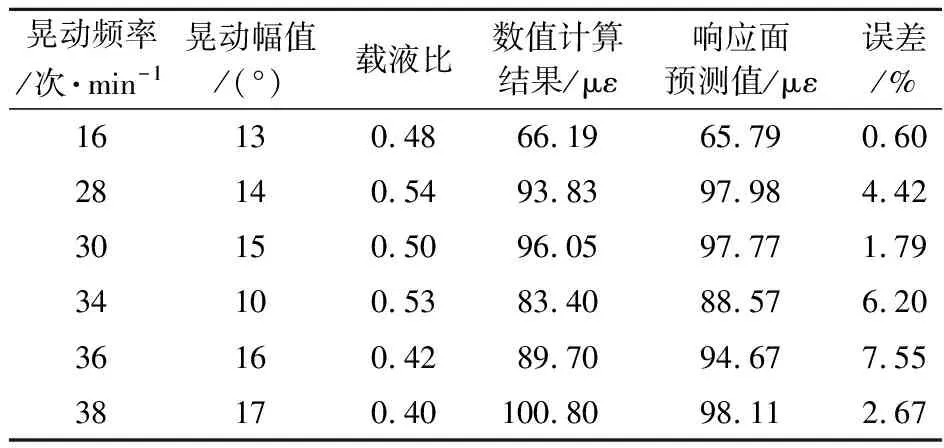
(1) 把自变量xi按区间等概率分为30个子区间,xi 0 (3) 多次重复步骤(2),并利用样本点之间最大距离最小化得到最优样本空间。 β=(XTX)-1XTy (2) 且本文有 针对1号主油箱,取有限元流固耦合分析中上蒙皮对应试验应变花15~19号贴片测试点中的最大主应变峰值为响应值,得到上蒙皮响应面函数为 FL+0.3AL+0.03F2+0.1A2-83.4L2 (3) 式中F为晃动频率,A为晃动幅值,L为载液比。 图2 上蒙皮贴片点 另随机选取6个工况,开展流固耦合数值计算得到主应变响应值。对比响应面函数预测值与工况点计算值,验证函数模型准确度。随机工况点数据及其对比结果列入表2。由表2可知,响应面函数预测结果与有限元计算结果最大误差为9.6%。值得注意的是,最大误差发生在响应数值较小的工况,响应数值大的工况对应较小的误差。出于安全性考虑,本文更多关注应变响应数值较大的危险工况,因此可认为响应面函数可以有效预测响应数值较大的危险工况。 表2 复材燃油箱上蒙皮代理模型数值分析验证 开展全尺寸复材燃油箱晃动物理试验以验证响应面函数正确性。表3为三种工况下函数预测值与试验值结果对比,1号主油箱的上蒙皮最大主应变函数预测值与试验结果误差在10%以内,满足工程要求。有限元数值计算和全尺寸物理试验表明,响应面代理函数可准确预测上蒙皮不同工况下的主应变峰值响应,可用于快速适航审定和最危工况预测。 表3 复材燃油箱上蒙皮代理模型物理试验验证 进一步分析复材燃油箱上蒙皮响应面函数随晃动幅值、晃动频率和载液比三个自变量的变化趋势,结果如图 3所示。当频率固定为20 次/min,幅值为15°时,最大主应变峰值变化趋势如 图3(a)所示,存在最危险载液比0.91使得主应变峰值达到最大。当固定载液比为0.7,幅值为15°时,如 图3(b)所示,响应面代理函数呈单调递增特性,主应变峰值随晃动频率增大而增大。当固定载液比为0.7,频率为20 次/min时,最大主应变峰值基本随晃动幅值呈递增趋势,如图3(c)所示。 图3 上蒙皮最大主应变峰值变化趋势 给定晃动幅值和频率时,存在载液比使响应面函数存在极大值,极大值对应的工况即是工程实际中应尽量避免和关注的危险工况。几种典型晃动工况下,最危险载液比列入表4,可知随着晃动频率与晃动幅值的增加,最危险载液比呈增加趋势。 表4 上蒙皮各工况最危险载液比 有限元流固耦合分析中,取1号主油箱下蒙皮1~5,7,37,38贴片点的最大主应变峰值为响应,得到下蒙皮响应面函数为 0.1FA+0.1FL-3.8AL-0.03F2+ 0.1A2-206.7L2 (4) 图4 下蒙皮贴片点 与上蒙皮类似,同样选取6个验证样本点开展流固耦合数值分析,验证响应面代理函数模型的准确度。验证样本点数据及其对比结果列入表5,下蒙皮响应面函数预测结果与有限元计算结果基本一致,最大误差为6.2%,相差仅为5.17 με。 表5 复材燃油箱下蒙皮代理模型数值分析验证 同样选取三组全尺寸机翼油箱晃动试验工况数据对响应面代理函数模型的准确性进行验证。由表6可知,三种工况下函数预测值与物理试验结果误差均在10%以内。数值分析和试验验证表明,响应面代理函数可准确预测下蒙皮不同工况下的主应变峰值响应,用于快速适航审定。 表6 复材燃油箱下蒙皮代理模型物理试验验证 分析下蒙皮响应面代理函数最大主应变峰值随晃动幅值、晃动频率和载液比三个自变量的变化趋势。给定晃动频率和载液量,存在最危险载液比使得响应函数取极大值。当频率为20 次/min,幅值为15°时,最大主应变峰值随载液比的变化趋势如 图5(a)所示,最危险载液比为0.93。各典型工况及其最危险载液比列入表7。同时,需要指出的是,相同工况下,下蒙皮最大主应变峰值比上蒙皮最大主应变峰值大。这是因为除自由液面晃动的影响外,下蒙皮还受到液体重力的影响,导致机翼下蒙皮变形增加,因此下蒙皮最大主应变峰值会较大。 图5 下蒙皮最大主应变峰值变化趋势 表7 下蒙皮各工况最危险载液比 当固定载液比和晃动幅值时,响应面代理函数为晃动频率的一元二次函数,在晃动频率范围内呈单调递增趋势。以固定载液比0.7,幅值15°为例,最大主应变峰值随晃动频率的变化趋势如图5(b)所示。当固定载液比与晃动频率时,下蒙皮最大主应变峰值会随着晃动幅值逐渐上升。以固定载液比0.7,频率20 次/min为例,最大主应变峰值随晃动幅值的变化趋势如图5(c)所示。 对于复材燃油箱下蒙皮,在给定晃动频率和晃动幅值时,存在一个最危险载液比使得最大主应变峰值最大。空载或满载时油箱不发生液体晃动,最危险载液比时液体晃动明显,液面与壁面之间存在相对运动,液体对壁面有动态压力作用,进而造成主应变呈非线性变化。固定载液比和幅值时,随着晃动频率的增大,周期晃动过程中的加速度最大值增加,油箱壁面对液体的作用力为液体晃动提供加速度,油箱内液体对壁面的压力增加,机翼变形增加,导致下蒙皮最大主应变峰值会随着晃动频率的增大而增大。固定载液比和晃动频率时,晃动幅值越大,液体惯性力对壁面作用越明显,从而最大主应变峰值随着晃动幅值的增大而增大。同时,相同工况下,下蒙皮最大主应变峰值变化趋势与上蒙皮一致,且下蒙皮最大主应变峰值比上蒙皮大,所以机翼油箱破坏多发生于下蒙皮位置。 本文通过拉丁超立方采样方法和响应面代理函数,以晃动频率、晃动幅值和油箱载液比为自变量,以油箱上下蒙皮最大主应变峰值为响应,建立了上下蒙皮响应面函数。流固耦合数值计算和全尺寸机翼油箱晃动试验表明了响应面模型的有效性。同时,本文基于响应面函数分析油箱晃动,发现随着晃动幅值和频率的增加,上下蒙皮最大主应变峰值响应呈非线性趋势,存在最危险载液比使得响应函数取极大值。此外,下蒙皮最大主应变峰值数值远大于相同工况下上蒙皮的主应变峰值,油箱破坏多发生于下蒙皮位置。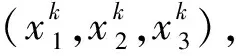
4 结果与讨论
4.1 油箱上蒙皮代理模型与最危工况预测


4.2 油箱下蒙皮代理模型与最危工况预测




5 结 论
