悬索桥空间缆索实用找形方法
2021-11-02马召宇许福友檀永刚
马召宇, 许福友, 檀永刚
(大连理工大学 建设工程学部,大连 116024)
1 引 言
随着悬索桥跨度的增加,其横向刚度和动力稳定性不断降低,因此空间主缆得到广泛采用,以提高悬索桥横向刚度和稳定性,如韩国永宗桥和杭州江东大桥等。另外,一些较窄的人行悬索桥,其主梁刚度和抗风稳定性相对较差,需要加设空间风缆,如河北平山红崖谷玻璃吊桥和日本九重梦大桥等。相比于平面缆索,空间缆索的线形计算应考虑主缆和吊杆的耦合效应,计算过程更为复杂。目前主要有分段悬链线法[1,2]SCM(Segmental Catenary Method)和有限元法两类方法。
罗喜恒等[3]以空间的主缆索段为研究对象,将SCM扩展至空间缆索的线形计算。李传习等[4]推导了悬索桥空间主缆线形变化刚度矩阵的递推公式,提高了SCM的计算效率。文献[5-8]基于空间分段悬链线理论对SCM加以修正,改善了其计算性能。SCM迭代参数少,求解速度快,是目前计算精度最高,应用最普遍的方法。但该方法对迭代初值敏感,迭代过程容易发散,且需要推导复杂的悬链线方程,编程求解非线性方程组,不便于一般工程师和科研人员使用。有限元法[9]更具有通用性,在方便应用、收敛性等方面相对SCM更有优势,也可以实现空间缆索的线形计算。文献[10,11]将悬链线理论和有限元法相结合计算缆索线形,计算过程过于复杂,耗时较多。Sun等[12,13]将计算拱桥合理拱轴线的思想用于悬索桥空间主缆的线形计算,提出了坐标迭代法。该方法收敛稳定,但仍需要编程实现,不便在通用有限元软件中应用。Xiao 等[14,15]将吊杆力等效为集中荷载,建立主缆的有限元模型,并通过ANSYS进行简单的代数运算和流程控制,实现了空间缆索的线形计算。该方法不需要复杂的理论推导和编程,但仍存在以下不足,(1) 当主缆跨度较大或空间效应明显时,由抛物线法指定迭代初值时,主缆节点坐标可能与真实值偏差较大,容易导致第一步迭代计算发散,为确保收敛需多次人为调整迭代初值; (2) 当主缆坐标更新量较大时,由于耦合效应吊杆力会明显变化,容易导致下一步迭代计算发散,为确保收敛,迭代时需采取增加临时约束或减小坐标更新量等人为干预措施,不便于操作; (3) 忽略了吊杆的垂度效应。
针对以上问题,基于ANSYS提出一种悬索桥空间缆索的实用找形方法。本文方法建立空间缆索纯索体系模型,以缆索节点坐标和单元内力为未知参数,采用小弹性模量法确定其初值,通过内循环参数更新外循环坐标修正的嵌套循环迭代计算空间缆索线形。通过2个算例验证本文方法用于横桥向和纵桥向斜吊杆空间缆索线形计算的精度和收敛的稳定性,并通过1个工程实例验证了本文方法用于工程实践的有效性。
2 空间缆索设计参数
悬索桥的风缆与空间主缆的受力特点和求解方法是一致的,但通常情况下,风缆横向矢跨比大于空间主缆,故风缆的空间特性更明显,线形计算难度更大,因此本文以悬索桥风缆为工程背景展开论述。如图1所示定义空间坐标系,x轴为顺桥向,y轴为横桥向,z轴为竖向。风缆有y和z两个方向的垂度,y方向垂度通常事先设定,z方向垂度需要计算;对于吊杆,在确定A1~An - 1坐标前,其线形和内力无法确定,B1~Bn - 1吊点处吊杆力y方向分量可以事先设定,z方向分量需要计算。因此,计算空间缆索线形时,设计参数如下。
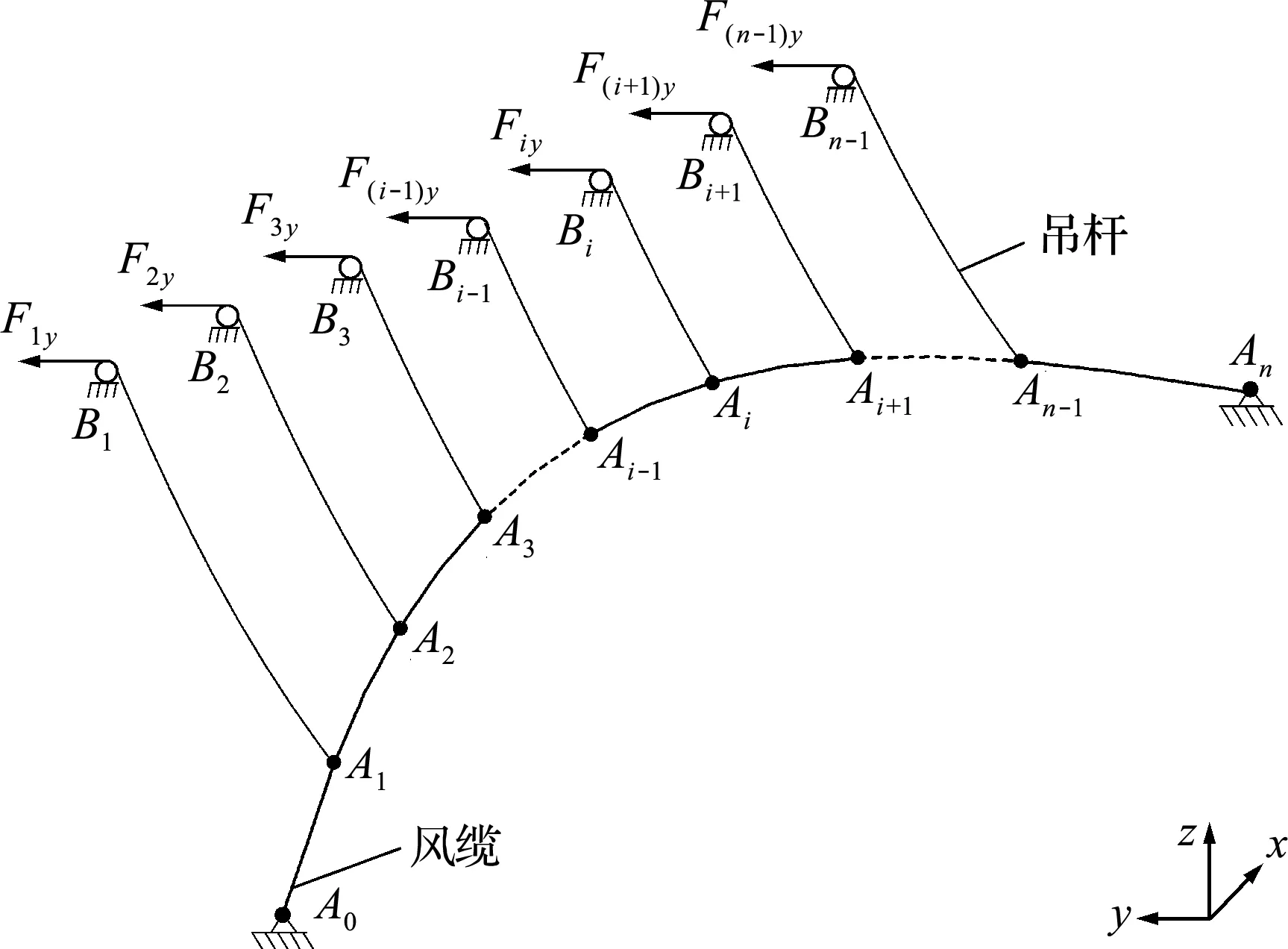
图1 风缆分析模型
(1) 风缆和吊杆的弹性模量、截面面积和材料密度等参数。
(2) 风缆A0和An两锚固点x,y和z坐标,A1~An - 1吊点的x坐标,控制点Ai的y坐标ycon。
(3) 吊杆在主梁上吊点B1~Bn -1的x,y和z坐标。
(4)B1~Bn -1吊点处吊杆力y方向分量设计值F1 y~F(n - 1)y。
3 空间缆索线形计算
采用有限元计算缆索线形属于典型的大变形小应变的几何非线性问题,通常采用迭代法计算,而线形计算过程中,有限元建模方法、迭代初值的确定和迭代算法均十分关键,任何一步操作不合理都可能造成计算发散。
3.1 基本假定
为了简化操作流程,避免复杂的理论推导,结合空间缆索的特点,本文基本假定如下。
(1) 采用杆单元(Link10)模拟风缆和吊杆,单元呈直线线形,且只能受拉而不能弯压,单元材料符合胡克定律。
(2) 将沿单元均匀分布的自重荷载转化为等效的集中荷载作用于单元节点上。
(3) 每根吊杆及风缆相邻吊点间的索段均采用一个或多个杆单元模拟。
3.2 建模方法
有限元模型是基于ANSYS计算空间缆索线形的基础,建模方法的优劣将直接关系到迭代过程的稳定性和结果的准确性。文献[14,15]采用仅包含主缆的模型,每步迭代时,根据吊杆力竖向分量和主缆节点坐标更新吊杆力,并施加于主缆节点上。采用该方法建模,当主缆坐标更新量较大时,由于耦合效应,吊杆力会发生明显变化,容易导致迭代发散。另外,将吊杆力等效为集中荷载忽略了吊杆的垂度效应,而引入悬链线理论又会增加算法的难度,不便于工程应用。针对以上问题,本文建模方法如下。
(1) 如图1所示,建立风缆和吊杆单元且均采用Link10单元模拟。
(2) 固结风缆A0和An两点,约束B1~Bn -1吊点x和z方向自由度,释放y方向自由度。
(3) 将吊杆力y方向分量的设计值F1 y~F(n -1)y作为集中荷载施加于吊点B1~Bn -1上。
(4) 索夹重量采用质量单元施加于风缆节点A1~An -1上。
基于以上方法建立的模型迭代计算空间缆索线形具有以下明显优势。
(1) 模型建立了吊杆单元,每一步迭代时直接将上步吊杆力计算值更新为下次迭代初值,避免了吊杆力更新变化导致的迭代发散。
(2) 模型自身可以考虑吊杆的垂度效应以及风缆和吊杆的耦合效应。
(3) 模型除了约束A0和An两点外,B1~Bn -1吊点的x和z方向均施加了约束,可以提高计算的稳定性。
3.3 迭代初值的确定
基于以上建模方法,以风缆和吊杆单元内力和节点坐标为未知参数,迭代计算空间缆索线形。迭代计算时,首先应赋予未知参数合理的迭代初值,否则很可能会造成第一步迭代计算的发散。文献[6,7]采用抛物线法确定迭代初值,对于空间效应明显的风缆,该方法确定的初值往往与真实值相差较大,容易导致发散,往往需要多次人为调整,不便于实际应用。为解决以上问题,采用小弹性模量法计算确定未知参数的迭代初值。所谓小弹性模量法,即在有限元计算时将索单元的弹性模量取小于真实值的2~3个数量级,使索单元获得较强的变形能力和稳定的收敛性。基本步骤如下。
(1) 如图2所示,以A0An直线为风缆初始线形建立初始有限元模型。

图2 初始有限元模型
(2) 赋予单元的截面积、线密度和小弹性模量(缩小103倍)。
(3) 赋予风缆和吊杆各单元相同且较大的初应变。
(4) 非线性求解,获得风缆和吊杆单元内力以及风缆节点y和z坐标。
(5) 计算控制点Ai的y坐标与设计值ycon的差值Δ1,若Δ1>Δcon1 -1,返回步骤(4);若|Δ1|<Δcon1 -1,则输出风缆和吊杆单元内力和风缆节点y和z坐标。
上述步骤确定的未知参数初值只需确保第一步迭代计算的收敛,对参数取值的精度要求不高,因此步骤(5)收敛容许值Δcon1 -1可以在0.1 m~0.5 m 范围内取值。工程人员一般试算2~3次即可确定步骤(3)合理的初应变值,进而获得满足收敛要求的迭代初值。相比于抛物线法,本文方法具有以下优势。
(1) 迭代初值由有限元计算确定,满足小弹性模量下力的平衡条件,相比于由抛物线法确定的初值更接近于真实值,故收敛性更好,不需要多次人为调整。
(2) 初始模型风缆和吊杆的线形均指定为直线,操作简便快捷,便于掌握。
3.4 迭代算法
基于有限元迭代计算空间缆索线形时,迭代方法的优劣将直接关系到计算的敛散性和求解速度的快慢。本文以风缆和吊杆各单元内力及节点坐标为未知参数,采用嵌套循环展开迭代计算,基本步骤如下。
(1) 根据3.3节输出结果更新有限元模型,恢复索单元的真实弹性模量。
(2) 非线性求解,获得风缆和吊杆各单元内力及各节点y和z坐标。
(3) 如图3所示,根据风缆控制点Ai的y坐标设计要求值ycon,对上次计算获得的风缆y坐标a进行修正,设c为过A0,(xi,Δ1),An三点的抛物线,将a减去c即为修正后的风缆y坐标b。

图3 风缆节点y坐标修正简图
(4) 更新各单元内力,以及风缆和吊杆各节点y和z坐标。
(5) 非线性求解,获得风缆和吊杆各单元内力及各节点y和z坐标。
(6) 获得B1~Bn -1节点y方向位移Δ2,若|Δ2|>Δcon 2,返回步骤(4);若|Δ2|<Δcon 2,则进入步骤(7)。
(7) 计算控制点Ai的y坐标与设计值ycon的差值Δ1,若|Δ1|>Δcon1 - 2,返回步骤(3);若|Δ1|<Δcon1 -2,则结束迭代,输出结果。
步骤(6,7)的收敛容许值Δcon 2和Δcon1 -2一般取10-6m即可满足工程精度要求,以上迭代算法在ANSYS中基于APDL语言实现。
本文迭代算法的内循环通过风缆和吊杆各单元内力及各节点y和z坐标的更新,确保B1~Bn -1节点y方向位移快速收敛于Δcon 2,内循环结束时|Δ1|可能不满足收敛条件,即风缆控制点Ai的y坐标与设计值ycon相差较大,故进入外循环进行风缆y坐标修正,由于坐标修正打破了上次内循环迭代结束时缆索的平衡状态,因此需要再次进入内循环迭代更新,由此内外循环依次交替进行,|Δ1|和|Δ2|即可快速满足收敛条件,进而获得满足已知设计条件的空间缆索线形。
4 算 例
采用上述方法对3个算例进行分析。其中算例1对横向斜吊杆空间缆索进行分析,并通过与SCM的计算结果进行对比,验证了本文方法的精度;基于算例1,进一步开展了24种工况的线形计算,并通过与SCM的对比,验证了本文方法的稳定性。算例2对纵桥向斜吊杆空间缆索进行了分析,并通过有限元软件Midas验证了本文方法计算纵桥向斜吊杆空间缆索线形的准确性。算例3对一座人行悬索桥风缆找形分析,验证了本文方法在工程实践中的有效性。
4.1 横向斜吊杆空间缆索
如图1所示,风缆两锚固点坐标分别为A0(-100,0,0) m和A15(80,25,20) m,吊杆吊点B1(-65,100,60) m和B14(65,100,60) m,控制点A8的y坐标为60 m,吊杆沿x方向间距为 10 m,吊杆在B1~B14点沿y方向的张拉力设计值为 45 kN。风缆和吊杆的截面积、弹性模量和线密度分别为62.80 cm2,158 GPa,528.78 N/m和 5.22 cm2,165 GPa,45.21 N/m,计算该空间缆索系统的线形和内力。
风缆和吊杆均采用Link10单元模拟,风缆沿x方向每2.5 m划分1个单元,共72个单元,每根吊杆划分5个单元,整个缆索系统共142个单元。本算例外循环共迭代10次,内循环累计迭代 92次,完成迭代。表1给出了本文方法确定的风缆节点初始坐标及最终坐标。为了便于对比验证,根据SCM编制Matlab程序分析算例1,SCM的计算结果以及本文方法与SCM的计算差值一并给出。
由表1可知,两种方法计算得到的风缆各节点y坐标几乎完全相等,z坐标最大相差0.11 mm,可见两种方法计算结果相差很小,说明本文方法有效可行,且精度与SCM一致。
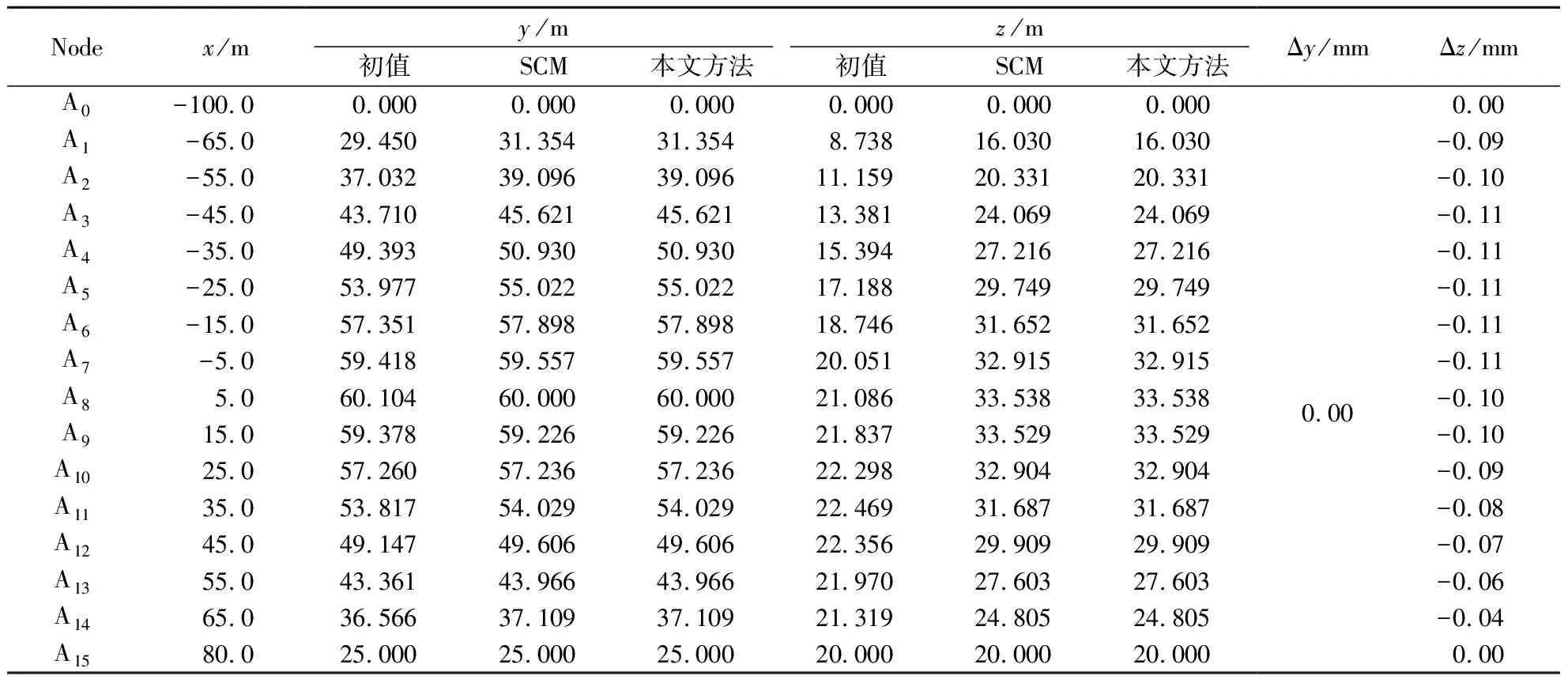
表1 风缆节点坐标Tab.1 Coordinates of wind cable nodes
为了验证本文方法的计算效率和稳定性,以算例1为基础,将风缆控制点A8的y坐标、吊杆横桥向张拉力、A15的y坐标和A15的z坐标分别设为 6种不同的数值,并在修改其中一个参数时,其余参数取值不变,共计得到24种工况,列入表2。采用本文方法对以上24种工况下的空间缆索线形进行计算,表2给出了内循环迭代次数,括号内第1个数值为采用本文方法的循环迭代次数,第2个数值为SCM的迭代次数。为了便于对比验证,SCM迭代次数也一并给出。
由表2可知,采用2种方法计算以上24种工况均全部收敛。SCM迭代次数较多,且迭代过程中为了保证收敛,需要多次调整迭代参数初值和修改松弛因子等人为参与。本文方法确定的初值不需人为调整即可保证第一步迭代的收敛,迭代过程中不需人为参与,具有良好的收敛性。可见本文方法人为参与程度低,计算效率高,具有很强的稳定性和可靠性,可以减少计算时间。
4.2 纵桥向斜吊杆空间缆索
如图4所示,目前一些悬索桥的风缆吊杆采用纵向倾斜的布置形式,为验证本文方法对纵向斜吊杆空间缆索线形计算的适用性,增加以下算例。风缆两锚固点A0和A9坐标分别为(-100,0,0) m和(80,25,20) m,吊点B1和B7坐标分别为(-65,100,60) m和(55,100,60) m,控制点A5的y坐标为60 m,吊点A1和A8的x坐标分别为-75 m 和65 m,吊点沿x方向间距为20 m,吊杆在B1~B7点沿y方向张拉力设计值为45 kN。风缆和吊杆的截面积、弹性模量和线密度分别为 62.80 cm2,158 GPa,528.78 N/m 和 5.22 cm2,165 GPa,45.21 N/m,计算该空间缆索系统的线形和内力。

图4 纵桥斜吊杆风缆分析模型
对于纵桥向斜吊杆的空间缆索,为使B1~B7吊点处x方向吊杆力相互平衡,采用本文方法开展迭代计算时,有限元模型应释放B1~B7吊点x方向的约束,本算例外循环共迭代10次,内循环累计迭代120次,完成迭代。表3给出了采用本文方法确定的风缆节点初始坐标及最终坐标。

表3 风缆节点坐标
根据本文方法计算得到的风缆和吊杆各单元无应力长度及各节点坐标,建立该空间缆索纯索体系的Midas模型,进行静力分析。由Midas模型静力分析得到的各节点位移均小于10-6m,且B1~B7吊点横桥向反力为45 kN,说明本文方法得到的计算结果是准确的,进而表明采用本文方法计算纵桥向斜吊杆空间缆索线形的可行性。
4.3 工程实例
一座单跨地锚式人行悬索桥,跨度为445 m。主缆理论矢高为45.0 m,矢跨比为1/9.89(图5),为提高桥梁抗风性能,桥面下方增设抗风缆。风缆具有以下设计要求,(1) 风缆和吊杆的截面积、弹性模量和线密度分别为 62.80 cm2,158 GPa,528.78 N/m 和5.22 cm2,165 GPa,45.21 N/m; (2) 上游侧风缆横桥向矢高为34.2 m,矢跨比为1/12.28,两锚固点顺桥向竖向和横桥向坐标分别为(-210,-25,40) m和(210,-25,40) m; (3) 风缆共设23根顺桥向间距为13.32 m的吊杆,吊杆在主梁上吊点的竖向和横桥向坐标为(-5.896,1.800) m,且横桥向张拉力为45 kN。依据以上设计要求,通过本文方法,风缆线形的计算列入表4。

图5 设风缆悬索桥平面及立面布置
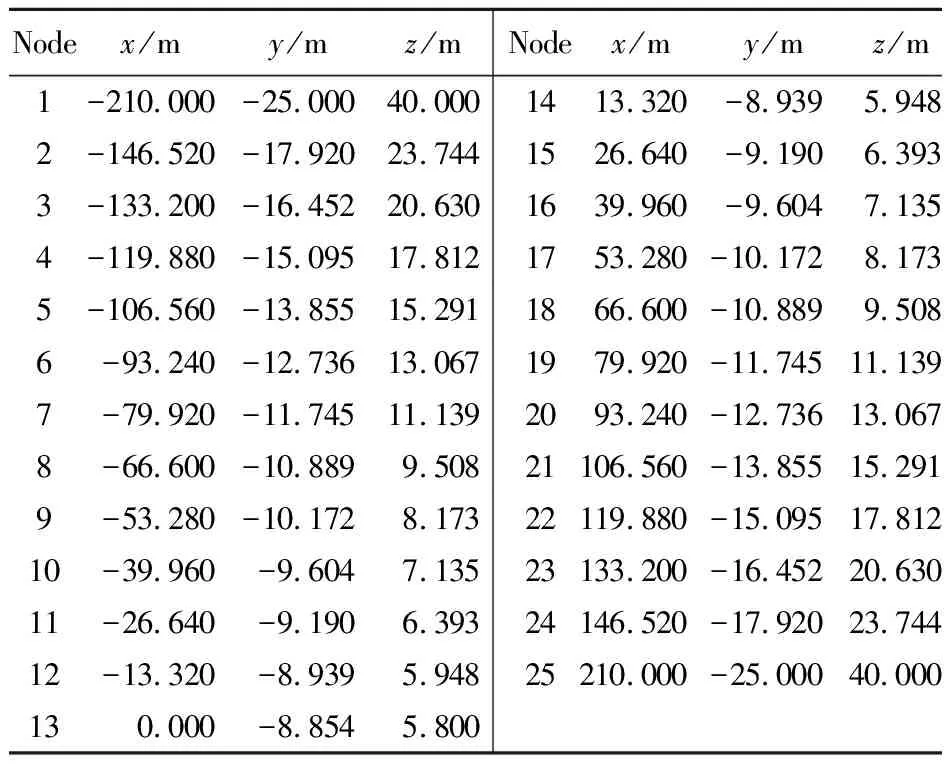
表4 风缆节点坐标
工程师在设计悬索桥风缆时,通常需要多次试算风缆吊杆横桥向张拉力,每次试算时风缆线形的计算都有较大挑战,尤其对于图6所示吊杆纵桥向倾斜设置的风缆更为突出。通过本文方法计算空间缆索线形,工程人员只需给出风缆设计参数,操作简便、快捷且稳定,为设置空间缆索的悬索桥的设计、施工和监控提供参考和借鉴。

图6 纵桥向风缆斜吊杆悬索桥平面及立面布置
5 结 论
(1) 基于通用有限元软件ANSYS提出了一种悬索桥空间缆索线形计算的实用方法,并给出了建立模型、确定迭代初值和迭代计算的详细步骤。
(2) 本文方法计算精度与SCM一致,但比SCM迭代次数少、稳定性好、计算效率更高,还适用于纵向斜吊杆空间缆索的线形计算。
(3) 本文方法操作简便快捷,不需要复杂的理论推导,人为参与程度低,具有较强的稳定性和可靠性,可供设计、施工和科研部门参考使用。
