PFC2D平节理模型细观参数标定方法

2021-11-02张宝玉张昌锁王晨龙郝保钦

计算力学学报 2021年5期

张宝玉，张昌锁*，王晨龙，郝保钦

(1.太原理工大学矿业工程学院，太原 030024；2.太原理工大学应用力学研究所，太原 030024)

1 引言

颗粒流程序PFC属于离散元法，可以解决非连续介质力学问题，并能从细观角度分析岩石的破坏机理。PFC用颗粒集合体来模拟岩石，通过定义颗粒间的黏结接触模型使得颗粒产生相互作用来重现岩石的力学性质。起初一般采用平行黏结模型(PBM)来模拟岩石，但研究发现PBM模拟岩石有如下缺陷[1-3]。压拉比过低，不能满足实际岩石的压拉比要求；内摩擦角偏小。为此，Potyondy[4]提出了平节理模型(FJM)，将圆形颗粒构造成多边形，可抑制接触破坏后颗粒的旋转，能够模拟出大压拉比。因此，本文采用FJM来模拟岩石。

2 平节理模型

平节理模型(FJM)是由晶粒及晶粒间赋予平节理接触(FJC)构成的，晶粒由圆盘颗粒和名义面(notional surfaces)组成，因此FJM相当于把颗粒构造成了多边形，可提供足够的自锁效应，抑制接触破坏后颗粒的旋转，能够模拟大压拉比情况。晶粒间的接触实际上是名义面间的接触，接触界面(interface)位于名义面之间。在PFC2D中，FJC是一条线段，该线段平均分成多段，每段代表一个单元，如图1所示。每个单元的状态是独立的，可以是黏结的或是非黏结的。黏结单元作用机理为，当其所受法向拉应力σ+>张拉强度σf时，单元破坏，生成张拉裂纹；当其所受切向应力τ>τf时，单元破坏，生成剪切裂纹。非黏结单元作用机理为，不能承受拉力；当其所受切向应力τ>τf时，沿接触界面发生滑移。其中，黏结状态和非黏结状态下的剪切强度τf分别见式(1,2)，

图1 平节理接触模型[4]

(1，2)

3 正交试验数值模拟

3.1 数值试验

进行数值试验包括建立模型和加载两个部分。

(1) 建立模型

首先，生成上下左右4面墙，墙围成的区域大小即为模型尺寸(50 mm×100 mm)；然后，按颗粒尺寸及分布形式在墙围成区域内生成重叠量较大的颗粒，计算弹开颗粒并使模型平衡；接着，通过伺服机制移动墙给模型施加一定的应力，使得颗粒体系均匀；模型中会存在少量悬浮颗粒(颗粒上的接触数少于3)，通过缩放这些悬浮颗粒的大小使其上的接触数≥3来达到消除悬浮颗粒的目的；最后，给模型接触赋予细观参数并将模型状态清零(包括颗粒速度和位移等)。建模完成后的数值模型如图2所示。

图2 数值模型

(2) 加载

单轴压缩试验。删除模型两侧的墙，给上下两面墙施加恒定速度来实现加载，通过上下墙监测轴向应力和应变，设置测量圆监测横向应变，据此可获取单轴抗压强度UCS、弹性模量E及泊松比ν。

直接拉伸试验。删除模型中所有的墙，在试样上下端给一定厚度颗粒恒定速度来进行加载，设置测量圆监测轴向应力应变，据此获取抗拉强度TS。

双轴压缩试验。根据伺服原理控制两侧的墙实现围压的施加，给上下两面墙施加恒定速度实现加载，并通过上下墙监测轴向应力，围压σ3和轴向应力σ1呈线性关系，

σ1=kσ3+b

(3)

(4)

(5)

3.2 试验参数选取

3.2.1 宏观参数选取

(6)

岩石的起裂强度σc i是判断围岩损伤范围的重要指标。在PFC中可通过裂纹数来确定岩石的σc i,文献[1，15]将裂纹数达到峰值强度对应裂纹数的10%时所对应的应力视为σc i。

3.2.2 细观参数选取

综上，本文研究选取的宏细观参数列入表1。

表1 选取的宏细观参数

3.3 正交试验设计

正交试验是研究多因素多水平的试验方法，主要是依据正交性在全面试验中选择具有代表性的点(试验点分布均匀)进行试验，用正交设计表来安排试验并进行数据分析，具有高效性，结果可靠简单易行[16]。

FJM中涉及很多细观参数，正交试验设计之前，为降低参数标定的难度，确定一些参数的值如下。

表2 因素水平

4 结果分析

表3 正交数值试验方案及结果Tab.3 Orthogonal numerical test scheme and results

4.1 多因素方差分析

方差分析(F检验)用于多个样本均数差别的显著性检验。根据方差分析计算过程[19]计算出试验因素及误差的自由度分别为3和7，查表可知显著性水平α=0.05时，F0.95(3,7)=4.35,显著性水平α=0.01时，F0.99(3,7)=8.45；计算各试验因素的F值并绘成图3。认为当4.35<因素F值<8.45时，因素对结果有显著影响；当因素F值> 8.45 时，因素对结果有非常显著的影响；因素的F值越大，其对结果的影响越大。据图3分析如下。

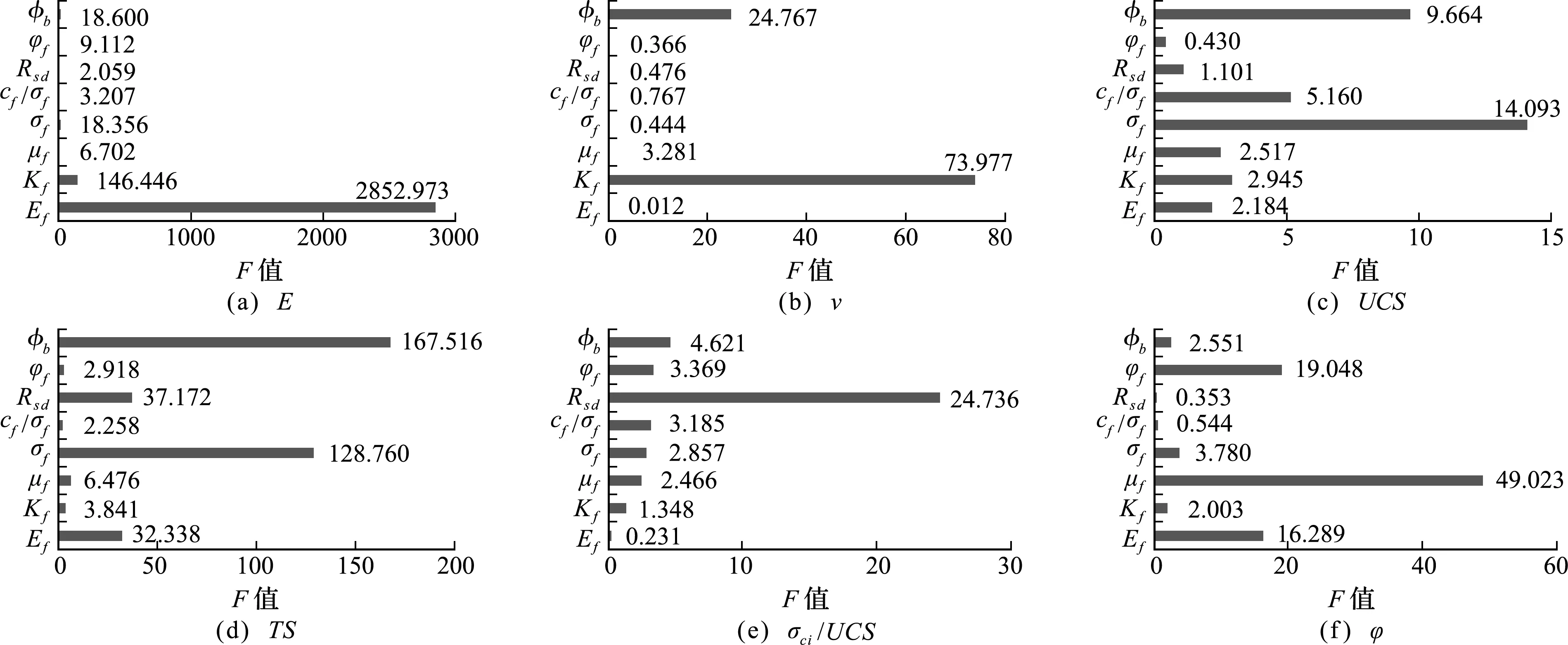
图3 多因素方差分析F值

4.2 回归分析

根据4.1节的分析，用岩石宏观参数的主要影响因素对其进行简单的线性拟合，结果见式(7～12)，可见只有式(7,8,10)的R2大于0.85，拟合效果较好，说明宏细观参数间的线性关系良好；其余公式的R2则较小，效果差，说明宏细观参数间的关系复杂，需要进一步分析，因此将试验结果平均值变化趋势绘于图4，分析如下。

图4 试验结果平均值变化趋势

E=0.858Ef-4.677Kf+12.021，R2=0.976

(7)

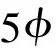
(8)

UCS=-0.037Ef-10.397Kf+31.312μf+

3.333σf+4.378(cf/σf)-41.644Rs d+

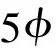
R2=0.819

(9)

Ts=0.007Ef+0.25σf-6.145Rs d+

R2=0.867

(10)

R2=0.607

(11)

R2=0.798

(12)

(1) 图4(a)显示，Ef和kf对E的影响趋势线变化很明显，且Ef和kf与E均呈良好的线性关系，而E随其余参数的变化趋势线基本水平。因此，用E的主要影响因素Ef和kf对其进行简单线性拟合的效果就很好，见式(7)，对应表4中第1个公式。

表4 宏细观参数间的拟合公式

5 细观参数标定流程及实例验证

5.1 FJM细观参数标定流程

图5 标定流程

5.2 实例验证

刘翌晨[21]从齐热哈塔尔引水隧洞中钻取片麻花岗岩试样进行物理试验来获取其宏观力学参数，试验结果平均值列入表5，本文以此为依据，进行片麻花岗岩的细观参数标定。

表5 片麻花岗岩试样宏观参数试验值和模拟值

表6 片麻花岗岩细观参数标定结果

数值模拟及物理试验得到的单轴压缩应力-应变曲线如图6所示，其中编号为Y-1,Y-2,Y-3和Y-4的曲线分别是物理试验中4个试样对应的结果。可以看出，模拟得到的曲线表现的特征与物理试验得到的曲线表现的特征接近，但数值模拟得到的曲线没有体现压密阶段特征(应力-应变曲线轻微下凸)，这是由于在建模过程中为得到均匀的颗粒体系进行了伺服，压密了颗粒体系，因此施加上应力即出现弹性变形特征(应力-应变曲线近似直线)。