复合绝缘材料介电性能的相场模拟研究进展
2021-11-02郭玉金董紫薇李庆民韩智云李志辉
郭玉金, 董紫薇, 李庆民, 韩智云, 李志辉
(新能源电力系统国家重点实验室(华北电力大学), 北京 102206)
1 引言
随着电力系统运行电压与容量的进一步提高以及与能源互联网的交叉融合,第三代电网属性对工程电介质的绝缘性能和调控设计提出了更高要求[1-4]。研究多场耦合作用下绝缘材料的劣化过程与损伤机理以及新型电介质的设计合成已成为高电压与绝缘技术学科的重要研究方向。作为新型高性能绝缘材料,纳米复合电介质受到广泛关注。人们针对新型复合电介质的制备、表征和介电性能的提升机制开展了大量工作,特别在击穿性能的改善和机理研究方面,关注了纳米粒子种类[5,6]、表面改性[7,8]和分散性对绝缘特性的影响。复合电介质材料的宏观特性,不仅取决于填料的种类和原子层面的本征属性,还取决于介观尺度下的微观结构,其关键问题在于实现复合电介质的结构调控设计。
随着计算机技术的飞速发展,数值模拟在复合电介质的研究中发挥越来越重要的作用。一方面计算机模拟已成为一种重要的辅助方式来模拟实验中难以原位观测到的局域介电响应,如介电击穿过程;另一方面数值模拟可以取代传统的试错试验,有效指导材料的结构设计,验证材料的有效性和可靠性。
相场模拟(Phase-Field Method,PFM)是计算材料科学分支的重要组成部分,是介观尺度下各类功能材料微观结构模拟与性能预测的有效手段[9]。相较于传统的突变界面模型,相场模拟方法采用了在界面处连续变化而非突变的序参量,避免了实时追踪界面的困难,从而大大简化了求解算法。在模拟系统的自由能泛函中,可考虑不同外场作用下的能量方程和动力学方程,使得相场模型在微结构演化与外场响应模拟等领域具有广泛的应用前景。
在高电压与绝缘技术领域,利用相场模拟研究绝缘材料在不同外场作用下的演化过程,从介观尺度揭示绝缘材料的劣化与损坏过程,预测材料微结构与性能的关联规律,理解材料宏观性能的微观机制,进而设计合成新型的电介质材料,是开展相场模拟的主要目的。本文系统概括了相场模拟方法的理论基础,梳理了其在复合绝缘介电性能研究中的应用进展,并给出了尚待深入开展研究的关键问题。
2 相场方法的物理内涵与数学表征
在复杂界面形貌演化中,突变界面的位置会随时间而变化,采用特定的突变界面动力学方程求解将变得非常复杂。相场模型通过将不同的界面描述纳入,可避免对复杂界面情况的直接跟踪处理。在扩散界面模型中,化学结构的非均匀性由两类序参量表征:保守序参量和非保守序参量。保守序参量满足局部守恒定律,典型示例包括多组分或多相系统中化学物种的原子密度和浓度;非保守序参量的典型示例包括化学有序的长程序参量,铁磁和铁电相变的磁化、极化以及位错和微裂纹的非弹性位移或非弹性应变等。这些序参量定义为连续场的时空函数,在相场模型中被称为相场参量。
为利用扩散界面模型预测复杂界面形貌演化的独特能力,在相场模型中需选择并定义合适的物理量作为序参量。这在某些问题中似乎并不困难,例如:反映共存相之间晶体对称关系的局部成分和长程序参量;在铁电材料相变中,电极化强度可以作为序参量;铁磁材料相变中,磁极化强度可作为序参量。而在凝固和晶粒生长等建模中,序参量的选取是具有挑战性的[10]。通常地,通过引入简单的唯象序参量来区分液体和固体以及晶粒取向。用唯象序参量建立的相场模型,被认为是描述复杂几何结构演化过程中避免边界跟踪的数值分析技术。如何定义物理上有严格内涵且计算上易于处理的序参量,从而建立物理自由能模型而非唯象自由能模型[11],并用相场方法预测复杂界面的基本性质,目前仍是一大挑战。
2.1 自由能泛函
在选择和定义好描述系统的序参量后,首要任务是准确给出系统的自由能表达式。对于以浓度作为序参量的非均匀二元系统,J.W.Cahn和J.E.Hilliard给出了一种自由能表达式[12,13]。总自由能不能仅取决于局部组成,还应包含非局部能量。因此假设对于一个非均匀体系,自由能既取决于组分还取决于其导数,从均匀自由能密度开始,用组分导数进行泰勒展开。对于各向同性材料,自由能简化为:
(1)
式中,c为组分的浓度变量;f0为均匀自由能密度,由各项自由能的加权平均和相间势垒组成;κ1~κ4为展开系数。同时认为,具有偶数次幂的派生项▽2c,▽4c,▽6c,…,应该舍弃,只保留二阶项,得到了Cahn-Hilliard自由能泛函:
(2)
式中,F为体系总能量的泛函表示;κ为梯度能系数。
对于复杂的材料系统,自由能泛函不仅依赖于成分场c,还依赖于非保守序参量η。A.A.Wheeler[14,15]开发了用于模拟二元合金等温相变的自由能泛函:
(3)
式中,f(c,η) 为均匀自由能密度;κc和κη分别为组分c和相场η的梯度能量系数。在没有界面能的情况下,均匀自由能密度是由一个插值函数和双势阱函数组成[16,17]:
f(c,η)=(1-h(η))fα(c)+h(η)fβ(c)+wg(η)
(4)
式中,g(η)为双势阱函数,在η= 0和η= 1处有最小值;w为能量势垒;将共存相fα(c)和fβ(c)的自由能组合成一个共同的自由能表达式;h(η)为无量纲插值函数,并且满足h(η=1)=1和h(η=0)=0,同时在η= 0和η= 1处有局部极值。选择插值函数只是为了便于数值计算,而不存在任何物理推理。更多关于插值函数的讨论可以参考N.Moelans[18]的工作。
多相和多组分的引入导致了另一类相场模型的发展,L.Q.Chen给出了包括许多非保守序参量的自由能泛函[19]:
(5)
其中
(6)
式中,ηi为序参数;u,v为唯象参数;κi为梯度能量系数;p为总变量数。
在上述模型当中,界面的宽度与物理宽度相同,界面的描述符合热力学一致性,但对模拟实际尺寸的微结构造成了严重限制。I.Steinbach等人促进了多组分和多相系统一系列的模型开发,且这些模型已在实验尺度上进行了定量模拟[20-22]。根据他们的研究,对于多相多组分体系,自由能泛函可简化为[23]:
(7)
其中
(8)
式中,Wα,β>0促进了相之间的平均场相互作用;积分中的后两项为非均匀自由能密度,包含相场和浓度场梯度的贡献;λα,β和κi,j分别为相场和浓度的梯度能系数;N1为总相数;N2为总组分数。
如果相变涉及到弹性位移,则需要将弹性应变能表示成场变量的函数,对于涉及带电物质或电磁偶极子的其他过程,可以使用类似于弹性能的方法评估电能或磁能对总自由能的贡献。对于电荷和偶极子的任意分布,必须首先求解静电平衡方程,解决电场和磁场分布,然后将总的静电能表示为场变量的函数。将所有外场的贡献考虑在内,自由能泛函的通用表达为[24]:
(9)
式中,fbulk为局部化学自由能;fgradient为由于序参量的不均匀分布而产生的梯度能;fel为相变发生弹性位移而产生的弹性能;fapply为附加能量项。
综上所述,对于不同的研究对象,序参量和能量泛函的形式存在较大差异,但是,几乎所有的相场模型仍然存在以下共同之处:第一,能量泛函中都包含了在界面处因序参量的不均匀分布产生的梯度能;第二,局部化学自由能函数一般采用双势阱形式,序参量可以取不同的稳定值。对于一些复杂的材料系统,为了更好地描述体系的化学组成和微观结构,需要定义多种序参量,同时还需考虑不同序参量之间的耦合。
2.2 相场动力学方程及其求解方法
在相场模拟方法中,相场变量的时间演化由一组耦合偏微分方程给出,除了少数只涉及传统尖锐界面的凝固模型外,这些方程是根据非平衡热力学原理推导出的[25,26]。对于相场方程的热力学推导的全面描述,可以参考文献[27]。浓度场ci等保守序参数的演化,遵循Cahn-Hilliard非线性扩散方程[13]:
(10)
式中,r为位置矢量;M为组分移动特性参数。非保守序参量ηt的演化遵循Allen-Cahn弛豫方程[28]:
(11)
式中,L为界面移动特性参数;t为非保守序参量的总个数。
事实上,上述两个方程均为系统自由能最小化的简单近似表示。设描述体系的场变量集为{φi,▽φi},对总自由能泛函F对时间求导并利用分部积分法,可得:
(12)
(13)
本质上而言,式(10)是局部平衡方程的反映,而式(11)不是从基本物理规律导出的,只是自由能最小化的最简单近似,但大量的相场模拟研究表明,式(11)可以很好地描述非保守序参量的演化。
式(10)和式(11)本质上是偏微分方程,很难得到其解析解,必须选用合适的数值求解方法。大多数相场模拟的求解采用有限差分方法,在空间上采用二阶有限差分离散,在时间上采用前向欧拉差分。但是,对于这样的显式步进方法,时间步长必须非常小,以保持数值解的稳定性,有时采用后向时间步进来改善稳定条件,这样处理会生成一个耦合的非线性代数方程组。方程求解首先需要线性化,例如使用牛顿-拉夫逊法,并且需要采用迭代技术,例如共轭梯度法或多重网格法来求解大型方程组。有限差分方法可与Neumann、Dirichlet以及周期性边界条件结合使用,且编程实现简单,在早期相场模型中被广泛应用。
在周期性边界条件下,经常使用的方法是快速傅里叶变换,该方法将积分微分方程转换为代数方程。或者,可先将积分微分方程转换为有限差分方程,然后将其转化到傅里叶空间。在倒空间中,采用前向欧拉差分进行时间步进求解,然后采用傅里叶反变换把倒空间下场变量的值转换到实空间。对于固态相变,通常采用具有半隐式时间步长的傅立叶谱方法[29,30],该方法的优点是可用隐式处理梯度项,无需求解大型的耦合方程组。频谱方法为二阶有限差分离散化提供了更好的空间精度,并且半隐式允许的时间步长比显式大一个数量级。但是,傅里叶光谱法仅适用于周期性边界条件的系统,对于其他边界条件则可采用切比雪夫谱方法[31]。对于与更复杂的几何形貌和任意边界条件的微结构演化相关的计算问题,有限元法更为实用[32]。
目前,大多数相场仿真工作采用课题组编写的内部代码,如Fortran、C++和Matlab程序[33]。这在一定程度上阻碍了相场模拟的广泛应用,同时也使得相场相关的论文结果难以再现。随着计算机技术的飞速发展,已涌现出了许多商业或开源的数值计算软件,利用这些已经存在并经过验证的软件包可最大限度地减少研究人员的编码工作。图1列出了目前最常用的具有相场模拟功能的商业软件以及开源工具[34]。加粗黑圈表示编码语言,虚线圈表示开源软件,加粗虚线圈表示商业软件,黑圈表示有限元求解器。开源的相场模拟工具是实现完整开源多尺度仿真框架的一个重要部分,可将相场模拟与密度泛函理论、分子动力学模拟、机器学习等先进的仿真工具相结合。

图1 具有相场模拟功能的软件列表Fig.1 List of software with phase field simulation capabilities
3 复合绝缘介电性能现场模拟研究进展
3.1 相场法在复合电介质构效关系研究中的应用
复合电介质中的纳米粒子与聚合物基体形成了大量复杂的界面区,进而改变了电介质的介观结构和微观参数,使复合电介质具有单组分介电材料无法达到的独特性能。目前针对复合电介质已开展了大量的实验研究,如LDPE/Al2O3、PI/SiO2、PI/BN、EP/SiO2等。复合电介质的性能不仅取决于各自组成材料(即基体和填料)的性能,还敏感地取决于嵌在基体中的填料微观结构(即尺寸、形状和空间排列)。了解填料的微观结构对复合电介质的影响是复合电介质设计和优化的核心问题之一。由于复合电介质微结构的复杂性,研究具有真实多组分微结构的复合电介质通常需要数值计算的方法,边界积分法[35]和有限元法[36]分别是计算复合系统中界面电荷密度分布和空间电势分布的常用计算方法。两种方法均采用细化微观结构的空间离散,即离散网格与复合材料多相微结构的界面相吻合。因此,不同的微观结构需要进行不同的网格剖分,数值的复杂度随着复合材料微观结构的复杂度增加而增加。为了避免这种复杂性,相场方法常被用于进行复合材料的计算研究。
密歇根科技大学的Y.U.Wang首次开发了相场模型来计算材料内部场的不均匀分布以及介电复合材料的有效特性,研究了填料尺寸、大小和分布取向对复合电介质极化、电荷密度和局域电场的影响[37]。采用极化矢量场P(r)作为序参量建立了复合电介质的相场模型,外加电场作用下复合电介质系统总自由能为[38]:
(14)
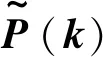
(15)
如图2所示,χM、χeff分别为基体和复合材料介电常数;箭头为电场方向。当填料粒子紧凑连接时,可有效缓解退极化效应,达到较高的有效介电常数。Y.U.Wang利用此相场模型研究了填充核壳结构的纳米颗粒对介电复合材料局部电场的影响,如图3所示,Ex、Ey为局部电场分量,壳层的存在抑制了界面处的电场畸变,有效减小了电场集中现象[39]。
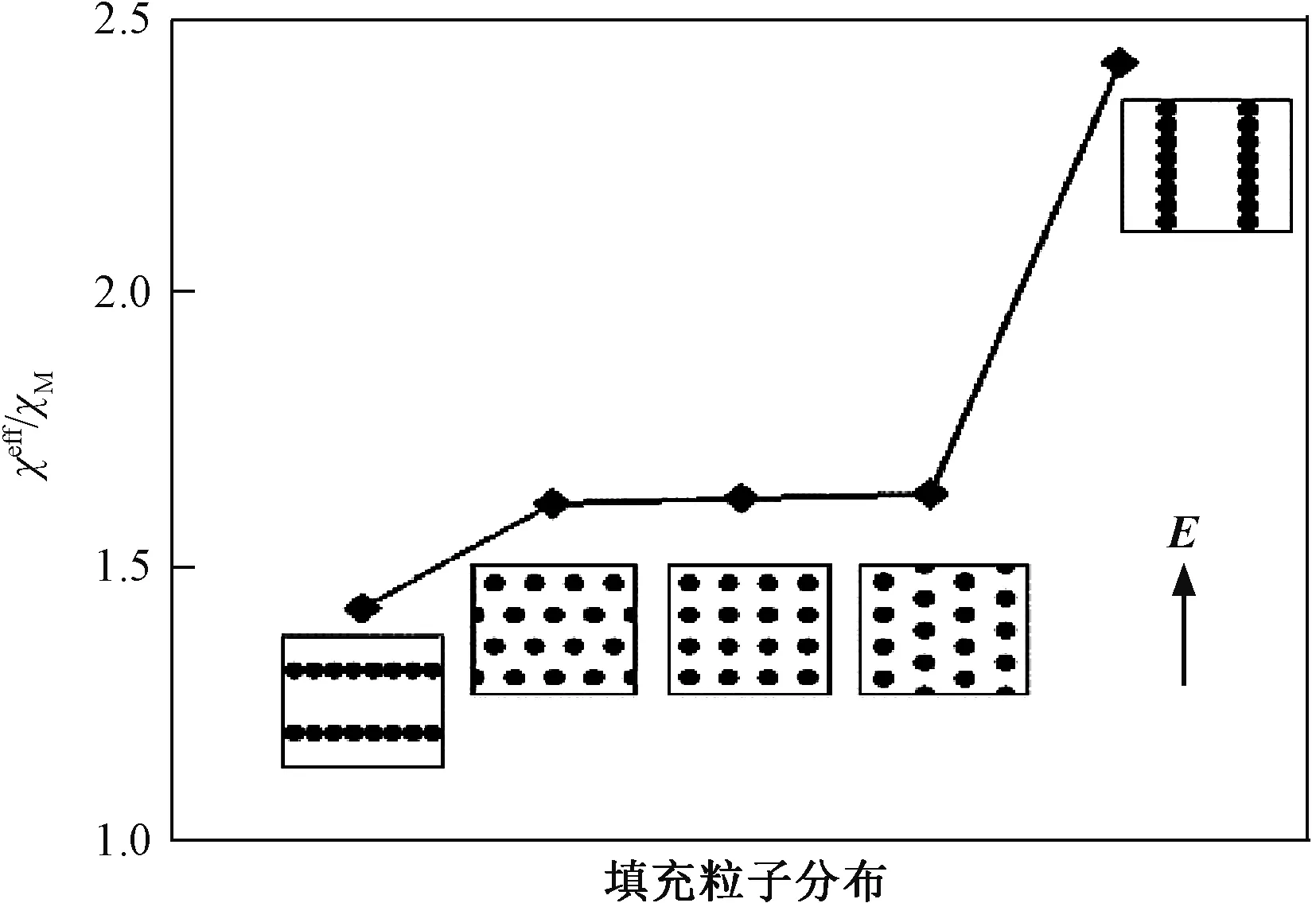
图2 填料的微观结构排列对介电常数影响[38]Fig.2 Effect of filler particle microstructural arrangement on effective dielectric constant[38]

图3 核壳结构纳米颗粒界面处的电场分布[39]Fig.3 Electric field distribution at interface of core shell nanoparticles[39]
Z.H.Shen构建了相场模型对如图4常见的复合电介质结构(垂直排列纳米线S1、垂直排列纳米片S2、随机分布纳米颗粒S3、平行排列纳米线S4、平行排列纳米片S5)进行了三维击穿模拟[40]。模型定义了一个连续的相场变量η(r)来表征复合电介质的损伤情况。介电非均匀系统的自由能考虑了相分离能、界面能以及静电能:
(16)
式中,fsep为驱动相分离的混合自由能密度;γ为各项同性近似下的梯度能量系数;felec为静电能密度。
这里定义一个不演化的序参数ρ来定义纳米填料(ρ=1)和聚合物基质(ρ=0),并通过一个插值函数将相对介电常数表示为序参数的函数:
(17)


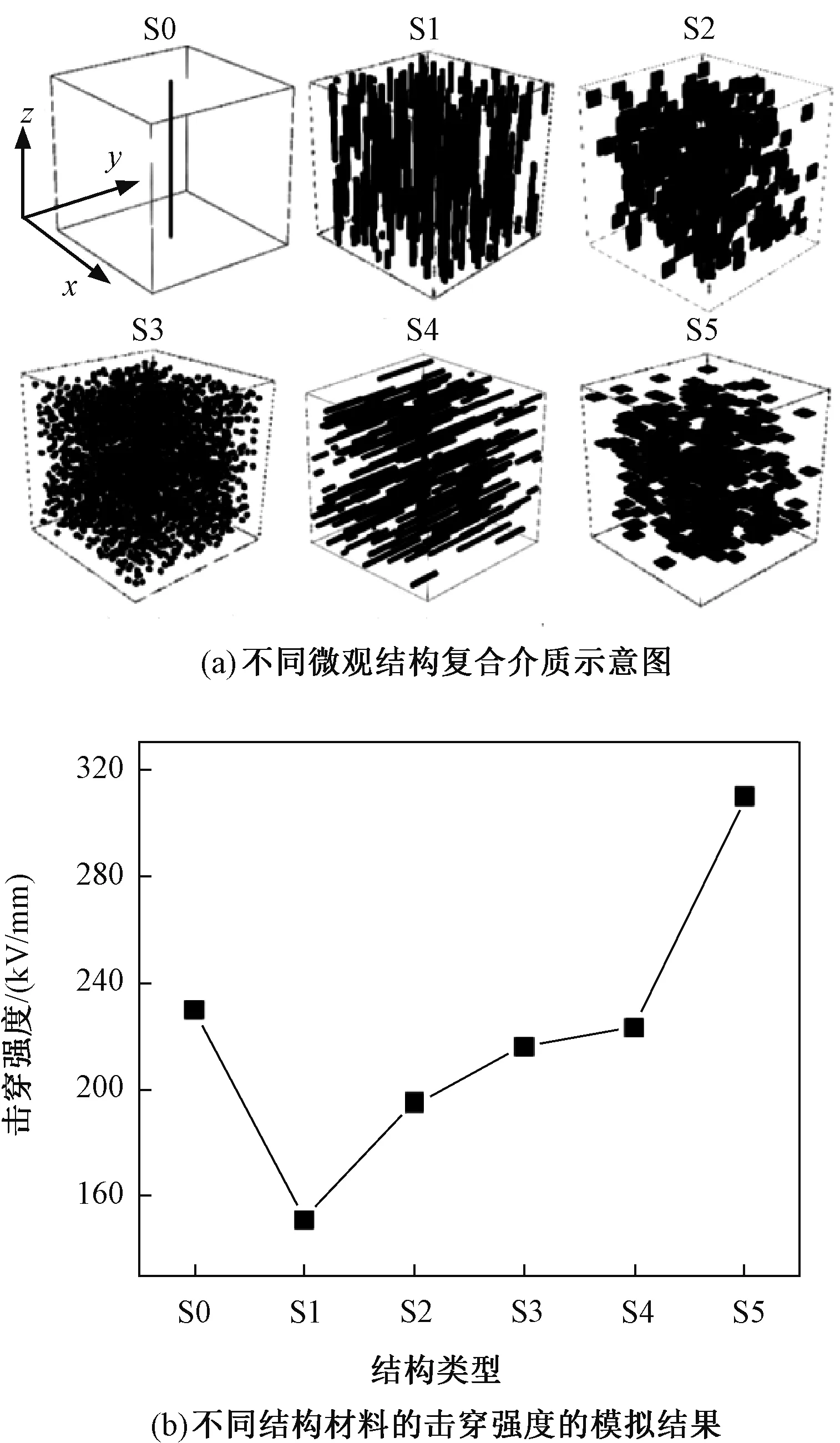
图4 填料结构对击穿强度的影响[40]Fig.4 Effect of filler structure on breakdown strength[40]

图5 界面对击穿强度的影响[41]Fig.5 Interface effect on breakdown strength[41]
3.2 相场法在电树演化和电介质击穿中的应用
绝缘击穿是发展高性能电介质材料必须研究的关键问题。目前,研究者对固体电介质的击穿进行了大量的研究,并提出了一些击穿机理,例如:电子碰撞电击穿理论、电子雪崩电击穿理论、电荷陷阱理论等。上述理论可以在一定程度上解释某些固体介质的击穿现象,但仍有很多击穿现象难以解释。作为实验的有效补充,建立了表征电树传播特性的数值模型。目前已有L.Niemeyer等人[42]提出的分形模型、M.D.Noskov等人[43]提出的随机模型和S. J. Dodd等人[44]提出的确定性模型。在分形和随机模型中,随机选择新的电树拓展来形成树的形状结构;对于确定性模型,计算累积损伤并与临界水平进行比较,以判断位置是否完全损伤。但是,由于复合电介质的介电非均匀性,使上述模型很难用于纳米复合材料。
电介质击穿是一个非常复杂的过程,当外加电场超过临界值时,电树枝可能从电场高度集中的薄弱点开始,并进一步拓展为完整的击穿路径,这一过程与裂纹拓展类似。裂纹拓展过程已用相场方法建模[45,46],借鉴裂纹拓展和脆性断裂的建模方法,研究者发展了电介质击穿的两类相场模型。Pitike和W. Hong首次开发相场模型研究固体电介质中击穿的产生和损伤演化过程[47]。模型引入一个连续的相场变量来表征损伤程度,假设初始状态下介质内部随机分布着一些高导电通道,采用Griffith型能量准则判断导电通道的生长。模型的自由能泛函表示为:
(18)
式中,E为电场;φ为电势;Wes为静电能密度;Wd(s)为损伤能量密度,Wd(s)=Wc[1-f(s)],Wc为静电能的临界密度;Wi为界面能。介电常数在两个极端状态下进行插值,即:
(19)
同时耦合泊松方程为:
(20)
使用此模型计算研究了电介质的击穿强度随厚度的变化关系,结果表明介质的击穿场强与厚度成逆幂函数关系;同时研究了填充粒子的介电常数、形状、取向对击穿性能的影响[48],结果表明圆形填料颗粒更容易引起电场集中,其抗击穿性能越差。
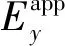
3.3 相场法在复合电介质结构设计中的应用
合成具有优异介电特性(击穿强度、介电常数、能量密度)的电介质材料需要合理设计复合材料的结构,具体包括纳米填料的物理参数、纳米填料-基体的界面特性以及纳米填料的几何分布等。但是,仅仅依靠高成本和反复的试错试验很难完成这项工作。材料的基因组计划提出,数值模型和计算机模拟取代传统的试错法,同时耦合尖端的材料表征技术,构建高度集成的高通量材料设计方法[55]。例如,通过分子动力学模拟计算筛选符合预期性质的分子结构,然后通过计算机辅助分析技术计算材料性能和可靠性,进而指导新材料制备和实验研究。

图6 不同温度下击穿演化和相应的能量密度分布[52]Fig.6 Breakdown evolution and energy density distribution at different temperatures [52]
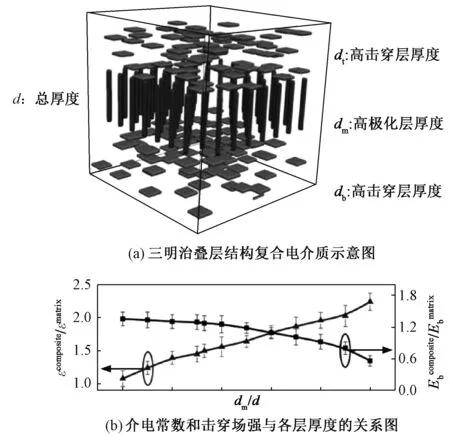
图7 基于高通量相场计算设计的夹层微结构[40]Fig.7 Designed sandwich microstructure based on high throughput phase field computation[40]

4 相场模拟有待解决的关键问题
(1)自由能泛函的构造。如前所述,确定系统总自由能泛函是相场建模的关键。对于不同的研究问题,系统自由能泛函有不同的表达。在目前的介电相场模型中,自由能泛函中序参数的化学能均采用了简单的双势阱形式,界面能采用了序参数梯度项的平方项。如何结合电介质击穿这一复杂过程,建立更加准确的物理自由能泛函,也是后续深化研究的关键问题。
(2)相场模型参数的确定。相场模型中包含了大量的唯象参数,必须确定这些参数才能获得准确的模拟结果。这些参数与共存相的热力学性质和平衡组分、界面能、界面宽度等有关。由于参数的数量很多,并且某些参数存在难以测量的属性,因此在相场模型中准确确定所有参数就变得异常复杂。原子尺度的第一性原理计算可提供有关难以测量的参数信息,例如界面能和迁移率及其各向异性。某些情况下,原子尺度计算难以直接获得全部参数,因此,相场模型还需耦合现有且不断完善的热力学和动力学评估数据库。但是,参数的确定仍然是相场建模中一个主要问题。
(3)相场方程的高效数值求解方法。在介电相场建模中,必须将相场动力学方程和泊松方程等耦合求解,目前的模型中多采用了傅里叶谱迭代摄动的方法求解静电平衡方程,并采用半隐式傅里叶谱方法求解相场方程。傅里叶变换要求的周期性边界条件不符合实际问题中复杂的边界条件。有限元法适用于任意边界条件及复杂几何形状计算,但是对于大规模的3D计算,有限元法的计算成本是不可接受的。因此,发展适用于实际工程问题中复杂边界条件高效的数值求解算法对相场模拟尤为重要。
(4)目前在介电相场模型中,只考虑了宏观特性参数,如介电常数、电导率、介质损耗因数等,没有考虑到介质内部的电荷传输过程。现有的研究工作已经实现了各自独立的动态演化过程(双极性载流子输运模型和击穿路径演化相场模型),实现两者的耦合同步模拟,对于认识电介质的老化与放电过程具有重要意义。此外,如何评估仿真和计算结果的准确度,以及计算机模拟如何有效指导实验设计,也都有待进一步解决。
5 结论
相场模拟技术经过多年的深入发展,已经成为计算物理和材料科学中一种功能强大的模拟方法。它基于包括界面在内的材料中非平衡态的热力学描述,通过一组保守和非保守的相场变量来表示微观结构。与经典热力学不同,相场模型中的自由能表示为相场变量及其空间梯度的函数。考虑不同的传输过程(如扩散、热传导、电流等)和能量方程,相场方法在关注微结构演化和外场响应等领域有着广泛的应用前景。
计算机仿真分析和辅助设计正逐步发展为与实验互补的研究手段,从微观层面协助研究者认识和理解实验无法解释的相关现象,并对实验设计提供有效指导和帮助。相场方法作为介观尺度下研究微观结构演化的强大工具,已经逐渐被用于研究复合电介质中的构效关系。结合高通量计算和机器学习等先进技术可以为复合材料的设计提供重要参考。
目前的介电相场模拟仍然处于定性、半定量研究层次,而相场模型的定量化发展需要精准的热力学和动力学参数。电介质的介电行为(如老化、击穿等)是一个非常复杂的过程,实际发生的物理过程包含多个时间和空间尺度,目前仍然需要发展结合第一性原理计算、分子动力学模拟等方法的多尺度仿真框架。
