电介质中极化电荷密度的计算

屈双惠，杨志宏，马志春，张彩霞

（石家庄学院 物理与电气信息工程学院，河北 石家庄 050035）

电介质中极化电荷密度的计算

屈双惠，杨志宏，马志春，张彩霞

（石家庄学院 物理与电气信息工程学院，河北 石家庄 050035）

给出了两种计算电介质中极化电荷密度的方法.（1）介质内部极化电荷密度等于极化强度矢量 的散度的负值，ρP=-▽·⇀P；（2）介质内部极化电荷密度与介质的极化率、介质内自由电荷密度以及极化率梯度与电场强度之间的相互作用有关针对电荷分布具有一定对称性的问题，分别利用这两种方法分析了电介质均匀且内部不存在自由电荷、电介质均匀但内部存在自由电荷以及电介质不均匀且内部不存在自由电荷情况下介质内部的极化电荷密度，并通过实例加以详尽的讨论.

极化率梯度；自由电荷密度；极化电荷密度

0 引言

当对电介质外加电场时，在电介质表面甚至内部会出现正负电荷，这种现象叫做电介质的极化.电介质上出现的极化电荷是其在电场作用下，内部电荷发生微小移动所造成的宏观效果，电介质中的带电粒子被原子或分子紧密束缚，其内电荷为束缚电荷.在现实应用中，由于电介质并不理想，可能是均匀的也可能是不均匀的，甚至其内部还有可能存在自由电荷的分布，这些都直接影响着电介质内部极化电荷的分布.因此，电介质的极化、其内部极化电荷的分布情况是一个难点内容[1，2].

对电荷分布具有一定对称性的问题，利用高斯定理可以很容易地求出其电场强度等物理量，进而确定其极化电荷分布.笔者给出了两种计算电介质中极化电荷密度的方法：

利用这两种方法分别讨论了电荷分布具有一定对称性时，电介质均匀且内部不存在自由电荷、电介质均匀但内部存在自由电荷以及电介质不均匀且内部不存在自由电荷情况下介质内部的极化电荷密度.

1 极化电荷密度的计算

当电介质极化时，介质内部的极化电荷分布与极化强度密切相关.由高斯散度定理，极化电荷密度等于极化强度矢量 的散度的负值：

自由电荷密度等于电位移矢量⇀D的散度：

对各向同性电介质，极化强度矢量⇀P及电位移矢量⇀D与介质极化率χe、电场强度⇀E的关系分别为

将两式分别代入（1）式和（2）式可得

消去（3）式和（4）式中的▽·⇀E，可得

（1）式和（5）式分别给出了求解电介质中极化电荷体密度的两种方法[3-5].

利用（1）式的方法，在求得极化强度矢量⇀P后，根据电荷分布特征，将其代入相应坐标系下的散度公式中求得▽·⇀P，即可求得极化电荷密度ρP=-▽·⇀P.当电荷分布具有平面对称性时，代入直角坐标系下散度公式中；当电荷分布具有球对称性时，代入球坐标系下散度公式中；当电荷分布具有轴对称性时，代入柱坐标系下散度公式中.

利用（5）式的方法，式中第1项由电介质体内自由电荷体密度ρf所决定，当介质体内无自由电荷时，该项贡献为零；式中第1项表示极化电荷还可能受到极化率梯度▽χe和电场强度⇀E的相互作用▽χe·⇀E的影响，当介质均匀或极化率梯度与电场强度相垂直时，该项贡献也为零[6-9].

以下针对电荷分布具有球对称性的问题分别利用这两种方法进行分析，并辅以案例加以讨论[10].

2 不同情况下极化电荷分布的案例分析

2.1 电介质均匀内部无自由电荷时的极化电荷分布

例1 一球形电容器由两个同心的薄金属球壳构成，两壳的半径分别为R1和R2，两壳间充满了电容率为ε的均匀介质，内壳带有正电荷Q，示意图见图1，求电介质内部的极化电荷密度 .

按方法（1）求解：电荷分布具有球对称性，利用有介质存在时的高斯定理得到电介质内距球心为r处的场点的电位移矢量此处的电场强度由于则 ，

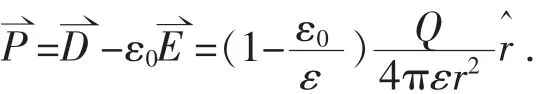
电荷分布具有球对称性，由（1）式，代入球坐标系下散度公式中可得

图1 均匀球形电介质不带电

按方法（2）求解：因为电介质均匀电容率ε为常数，则极化率为常数，▽χe=0，又因为电介质内无自由电荷，则ρf=0.根据公式（6），可知ρP=0.

通过例1分析可知，对于电介质均匀且内部无自由电荷的情况，电介质内无极化电荷，极化电荷只能分布在介质分界面处.电介质均匀，极化率χe为常数，极化率梯度▽χe=0；电介质内部不存在自由电荷，自由电荷密度ρf=0；利用公式（5）很容易看出，等式右侧两项均为0，其内部极化电荷密度为零.而利用公式（1）需要先求得极化强度，再将其代入到散度公式中进行求导方能求出极化电荷密度.可以看出，对于这种电介质均匀且内部无自由电荷的情况，利用方法（2）求解比较简单.

2.2 电介质均匀内部有自由电荷时的极化电荷分布

例2 半径为R的均匀电介质球，电容率为ε，均匀带电，总电量为Q，示意图见图2，求电介质内部的极化电荷密度ρP.

按方法（1）求解：电荷分布具有球对称性，利用有介质存在时的高斯定理得到电介质内距球心为r处的场点的电位移矢量此处的电场强度由于，则

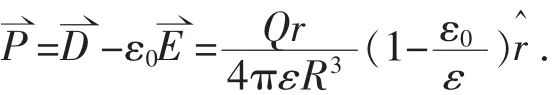
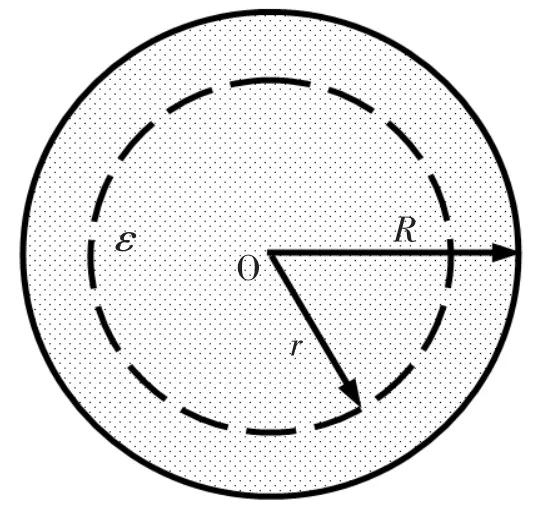
图2 均匀球形电介质带电

电荷分布具有球对称性，由（1）式，代入球坐标系下散度公式中可得

按方法（2）求解：因为电介质均匀电容率ε为常数，则极化率为常数，▽χe=0，式中第2项为0；自由电荷密度，根据公式（5），可知

通过例2分析可知，对于电介质均匀但内部有自由电荷的情况，电介质内部将出现未被抵消的极化电荷.电介质均匀，极化率χe为常数，极化率梯度▽χe=0；电介质内部存在自由电荷，自由电荷密度ρf≠0；利用公式（5）很容易得到极化电荷密度为而利用公式（1）也需要先求得极化强度，再将其代入到散度公式中进行求导方能求出极化电荷密度.可以看出，对于这种电介质均匀但内部有自由电荷的情况，利用方法（2）求解也比较简单.

2.3 电介质不均匀内部无自由电荷时的极化电荷分布

例3 空间有一同心球形电容器，其中外导体半径为R2，内导体半径为R1，在两层导体中间充满了不均匀电介质，其电容率为（ε0为真空电容率，k为常数，r为到球心的距离），内导体球带电量为Q，外球接地，示意图见图3，求电介质内部的极化电荷密度ρP.

按方法（1）求解：电荷分布具有球对称性，利用有介质存在时的高斯定理得到电介质内距球心为r处的场点的电位移矢量；此处的电场强度由于，则

图3 不均匀球形电介质不带电

电荷分布具有球对称性，由（1）式，代入球坐标系下散度公式中可得

按方法（2）求解：因为电介质内无自由电荷，ρf=0，式中第1项为0；电介质不均匀，电容率则极化率不为常数与此处的场强同向，式中第2项不为0；根据公式（5），可知

通过例3分析可知，对于电介质不均匀的情况，介质内部也会出现未被抵消的极化电荷.电介质内部无自由电荷，自由电荷密度ρf=0；介质不均匀，各处χe不同，极化率梯度▽χe≠0；由公式（5），此时极化电荷密度ρP由极化率梯度与电场强度的相互作用▽χe·⇀E所决定.若极化率梯度与电场强度垂直，即▽χe·⇀E=0，则ρP= 0；若极化率梯度与电场强度不垂直，则极化电荷分布由极化率梯度 与电场强度的点积决定，此时ρP≠0，电介质内有极化电荷存在.利用公式（5）求解极化电荷密度时，需要确定极化率梯度后再与电场强度点乘来获得.而利用公式（1）只需要求得极化强度的散度即可求出极化电荷密度.可以看出，对于这种电介质不均匀的情况，利用方法（1）求解比较简单.

3 结论

通过上面的分析发现当电介质发生极化时，其内部自由电荷密度ρP可由公式计算得到.当电介质均匀且内部无自由电荷时，电介质内部无极化电荷，极化电荷只分布在介质分界面处.当电介质均匀但内部存在自由电荷时，介质内出现未抵消的极化电荷.当电介质不均匀且内部无自由电荷时，若极化率梯度与电场强度垂直，电介质内部无极化电荷；若极化率梯度与电场强度不垂直，电介质内部将出现极化电荷.对于电介质均匀的情况，利用公式（5）求解比较简单，而对于电介质不均匀的情况，利用公式（1）求解相对简单.

[1]孙春峰.静电场作用下电介质的极化性质[J].物理与工程，2003，13（3）：27-31.

[2]任丽英，于斌.电介质极化的研究[J].西华大学学报（自然科学版），2008，27（6）：95-97.

[3]赵凯华，陈熙谋.电磁学[M].北京：高等教育出版社，1991：181-195.

[4]李文.关于电介质内部的极化电荷[J].辽宁大学学报（自然科学版），1997，24（2）：51-54.

[5]安宏.电介质的极化与电场的相互作用[J].物理与工程，2007，17（6）：13-18.

[6]赵玉华，张秋佳极化电介质球的电场及计算[J].哈尔滨理工大学学报，2007，12（3）：117-119.

[7]蒋明宇，胡先权，邓海.均匀电介质椭球内极化场强研究[J].重庆师范大学学报（自然科学版），2004，21（1）：41-45.

[8]李旭，李丽辉.均匀电介质椭球内极化场强方向与外电场方向的研究[J].首都师范大学学报（自然科学版），2003，24（2）：33-36.

[9]李旭，胡先权，胡文江.电介质椭球内极化场强方向的研究[J].大学物理，2004，23（10）：28-31.

[10]张之翔.电磁学千题解[M].北京：科学出版社，2002：188-189.

（责任编辑 钮效鹍）

Calculation Method of Polarization Charge Density in Dielectric

QU Shuang-hui，YANG Zhi-kong，MA Zhi-chun，ZHANG Cai-xia
（School of Physics&Electrical Information Engineering，Shijiazhuang University，Shijiazhuang，Heibei 050035，China）

Two calculation methods of polarization charge density in dielectric are given in this paper.（1）The polarization charge density is equal to the negative value of the polarization vector divergence，ρP=-▽·⇀P；（2）The po larization charge density is determined by the polarizability，the free charge density，the polarization gradient and the electric field intensityFor the situation of the charge distribution with certain symmetry，using the two methods，the polarization charge density is calculated respectively for the three cases：the uniform dielectric without free charge in it，the uniform dielectric with free charge in it，and nonuniform dielectric without free charge in it.It is discussed in detail by examples.

polarization gradient；free charge density；polarization charge density

O441

：A

：1673-1972（2014）06-0016-04

2014-06-20

河北省自然科学基金（F2013106079）；河北省教育厅科学研究计划（Z2010167）；石家庄学院2013年校级教学改革研究（JGXM-201302A）；石家庄学院2013年校级科研平台资助项目（XJPT002）

屈双惠 （1978-），女，河北石家庄人，讲师，主要从事理论物理和非线性系统研究.