基于子单元光滑有限元的混凝土相场损伤模型研究

吴卓恒

（华南理工大学土木与交通学院，广东 广州 510641）

混凝土是当今应用最为广泛的工程材料之一，然而作为一种准脆性材料，其在正常使用中会不可避免的出现裂缝，虽然现行《混凝土结构设计规范》[1]允许钢筋混凝土构件带裂缝工作，但这些裂缝则对构件乃至结构造成的不利影响仍是不可忽略的。

2018 年，Wu 提出的混凝土相场损伤模型[1]在给定相场尺度参数b 后仅需弹性模量、泊松比、单轴抗拉强度等容易获取的材料参数即可很好地模拟混凝土中复杂的开裂行为，有很广阔的应用前景。但该模型在通过有限元方法（Finite Element Method，FEM）进行求解时，由于需要保证相场梯度的精度，在潜在开裂区域附近往往需要划分较为精细的网格，这导致模型分析效率偏低。

2007 年Liu 等结合无网格法中的光滑应变技术，提出了光滑有限元方法（Smoothed FEM, S-FEM）[3]，其中子单元光滑有限元（Cell-based S-FEM, CS-FEM）算法简单，且在同网格下较FEM具有更高的计算精度。用其求解混凝土相场损伤模型的位移场与相场将有望提升求解精度，降低其对网格尺寸的要求，提升分析效率。

基于以上考虑，本工作将使用CS-FEM来求解混凝土相场损伤模型的位移场与相场，验证其求解相场损伤模型的能力，同时比较CS-FEM 在建议网格尺寸下的细网格和建议网格尺寸外的粗网格模拟结果的差异。

1 混凝土相场损伤模型

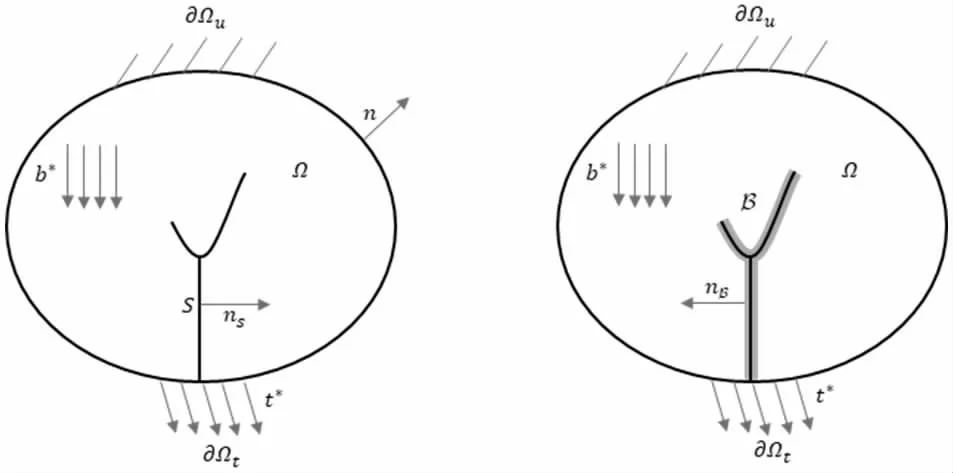
图1 混凝土相场损伤模型对裂缝的几何规则化

在混凝土相场损伤模型中，尖锐裂缝S 被弥散至宽度由尺度参数b 控制的损伤带B 中，固体其余部分ΩB 则不受裂缝影响。根据[1，3，4]，混凝土相场损伤模型的相关公式可整理为表1 所示的公式方框图。

表1 混凝土相场损伤模型公式

在混凝土相场损伤模型基于FEM的数值实现中，为保证求解精度，一般建议网格尺寸h 与相场长度尺度参数b 满足h≤b/5。

2 CS-FEM 基础理论与数值实现

2.1 光滑应变技术

在标准FEM中，固体的应变通过以下公式计算

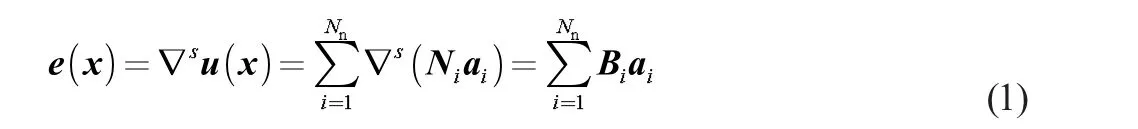
式中，Nn为模型中的节点总数，Ni为节点i 的位移插值形函数矩阵，ai为节点i 的所有位移自由度。

CS-FEM中采用的光滑应变技术则是在标准有限元应变场的基础上进行空间平均化处理。将求解区域划分为Ns个光滑域Ωsk，采用常数型光滑函数[6]，根据高斯公式可以得到边界上一维线积分形式的光滑应变场计算公式

式中，nx和ny分别为边界Γsk单位外法向量沿x 轴和y 轴方向的分量。

2.2 混凝土相场损伤模型在CS-FEM中的实现

CS-FEM中位移场与相场的通过以下的插值公式计算

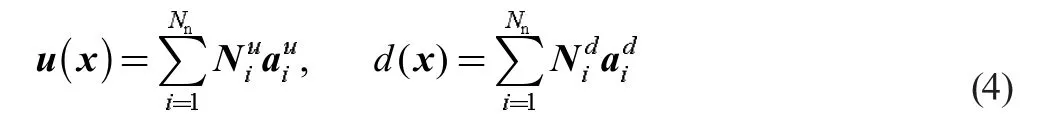
式中，Nui和Ndi为节点位移和相场的插值形函数矩阵，aui和adi分别为节点i 的所有位移自由度和相场自由度。

如图2 所示，CS-FEM 的光滑域是通过连接两条对边的中点得到的。相应的光滑后的应变和相场梯度表达式为

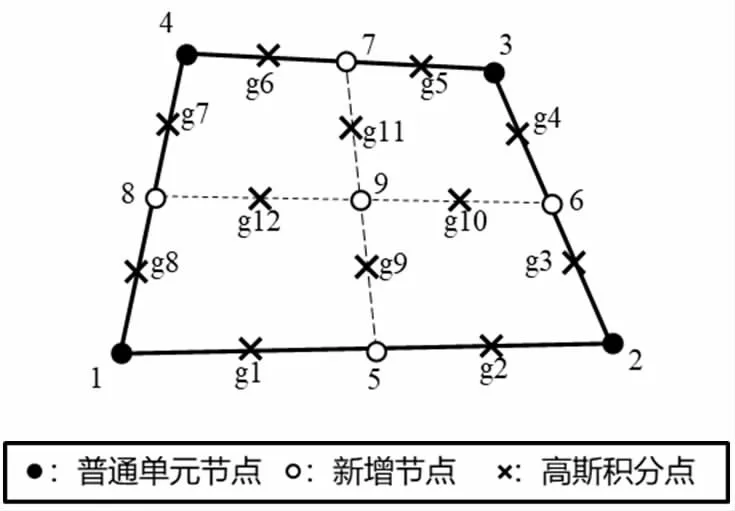
图2 CS-FEM 中的光滑域划分与积分的分布

式中，NsΓ为光滑域的边界数；xGp为边界上高斯积分点的坐标；lp为积分边界的长度。需要指出的是，整个过程不需要标准有限元中对单元插值形函数的求导以及单元的等参变换。

通过上述的离散过程，可以得到残量形式的控制方程

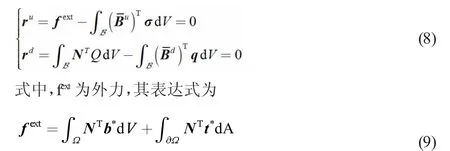
3 数值算例

考虑Winkler[7]的L 型板试验，试件的几何尺寸、加载方式与裂缝路径如图3 所示。模拟中采用Unger 等[7]建议的材料参数：弹性模量E0=2.0×104MPa，泊松比υ=0.18，单轴抗拉强度ft=2.5MPa，Ⅰ型断裂能Gf=0.130N/mm。相场长度尺度参数b 取为10mm。分别考虑大于建议网格尺寸的粗网格（h = b/2）和满足建议网格尺寸外的细网格（h = b/5）。

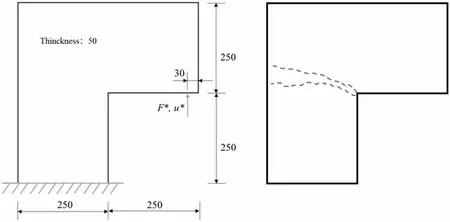
图3 L 型板试验：几何尺寸、加载方式与裂缝路径

模拟得到的开裂路径如图4 所示，可以看出基于CS-FEM的相场损伤模型在粗、细网格下得到的裂缝路径相同，且落在试验实测范围内。

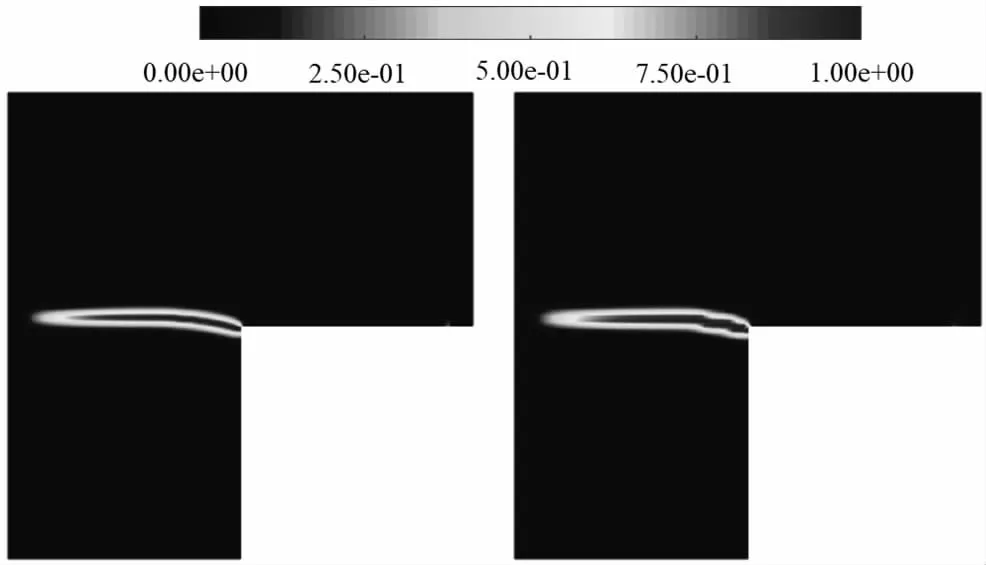
图4 模拟得到的开裂路径

模拟得到的荷载- 位移曲线如图5 所示，从中可以看出粗网格下得到的荷载较细网格下的结果偏大，但二者间差别很小且均落在试验实测范围内。

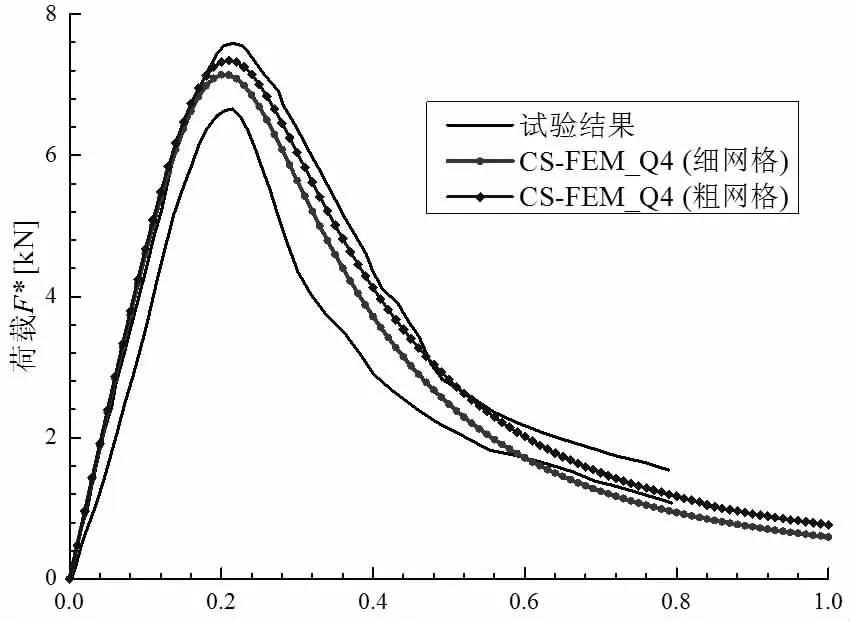
图5 模拟和试验得到的荷载- 位移曲线

4 结论

4.1 子单元光滑有限元（CS-FEM）能正确求解混凝土相场损伤模型。

4.2 CS-FEM在采用较FEM建议的网格尺寸（h≤b/5）更粗的网格（h=b/2）时同样能正确地模拟混凝土开裂破坏过程。