超导故障限流器抑制短路电流直流分量的仿真分析

倪 辉， 黎 炜， 兰润栋， 项 彬， 丁 培， 喻 婷， 赵 庆， 罗金辉， 姚晓飞

(1. 国网宁夏电力有限公司电力科学研究院， 宁夏 银川 750002； 2. 西安交通大学电力设备电气绝缘国家重点实验室， 陕西 西安 710049)

1 引言

随着我国社会的发展和国民经济的持续增长，电网规模越来越大。一方面，电力系统的装机容量逐年扩大，且随着特高压工程的逐步发展、新型能源的不断接入和电网联系的进一步加强[1-4]，系统短路电流的水平也随之增大，短路电流的直流分量也越来越大；另一方面，各种电力设备的X/R正逐渐增大，而为了限制短路电流水平采用的限流电抗器又进一步增加了系统的X/R值，使短路电流中直流分量时间常数不断增加[5-7]。文献[8,9]指出若触头分离时刻直流分量超过20%，则需考虑直流分量对开断性能的影响，直流分量会导致短路电流总的有效值增大，电弧能量增大，加大了断路器开断短路电流的难度。文献[10]将KEMA模型引入直流分量开断仿真，结果表明，当断路器的额定开断能力包含20%的直流分量时，气体燃弧的功率升高，临界电弧参数如散热功率常数比不考虑直流分量时大。综上所述，逐渐增大的直流分量使断路器的开断负担增大，严重时会导致开断失败，使整个系统崩溃。因此有必要研究抑制短路电流直流分量的方法，解决断路器开断能力不足的问题，保证系统的可靠运行。

目前，为解决短路电流超标，电网运行部门被迫采取主变停运、线路断线、母线分列运行、加装限流电抗器等方式限制短路电流[11-13]。上述运行方式的调整，或者降低了设备资产利用率，或者降低了电网供电可靠性，而加装限流电抗器又会使短路电流直流分量衰减时间常数增大，都会对电网的运行造成威胁。超导型故障电流限流器集检测、限流于一身，系统正常运行时不会产生损耗，系统发生故障时迅速反应，可抑制线路短路电流、降低对高压断路器开断容量的要求，且能自动恢复[14-17]，是保护电力系统最理想的限流装置之一。

然而，超导故障限流器对于短路电流直流分量和不同直流时间常数下故障情况的影响规律尚不清楚。本文的研究目标为获得超导故障限流器对于短路电流直流分量的抑制效果和不同直流时间常数下故障的影响规律，为系统选取合适阻值的超导限流器，为断路器分闸时间提供理论依据。本文通过在Matlab/Simulink中搭建超导限流器模型和系统电路模型，对比仿真了有无电阻型超导限流器、同一直流时间常数下不同阻值的超导限流器、同一阻值超导限流器下不同直流时间常数时系统发生故障的情况，对不同情况下的短路电流直流分量进行了分析，讨论了超导限流器失超电阻的选取方法。

2 仿真设置

2.1 仿真电路模型建立

在Matlab/Simulink模块中搭建图1所示的模型。图1(a)模拟电路发生短路的情况，交流系统为330 kV，线路电阻Rline=0.52 Ω，线路电抗Lline=0.023 5 H，负载电阻Rload=7.24 Ω，负载电抗Lload=0.326 5 H，此时线路的直流时间常数为45 ms，额定电流为3.0 kA，短路电流峰值为110 kA，稳定值为63 kA。图1(b)为模拟系统安装超导限流器后发生短路的情况。图1(c)模拟只存在线路阻抗并且超导限流器变化和图1(b)中短路时一样，目的为提取图1(b)系统发生短路时随着超导限流器电阻变化而变化的交流分量。

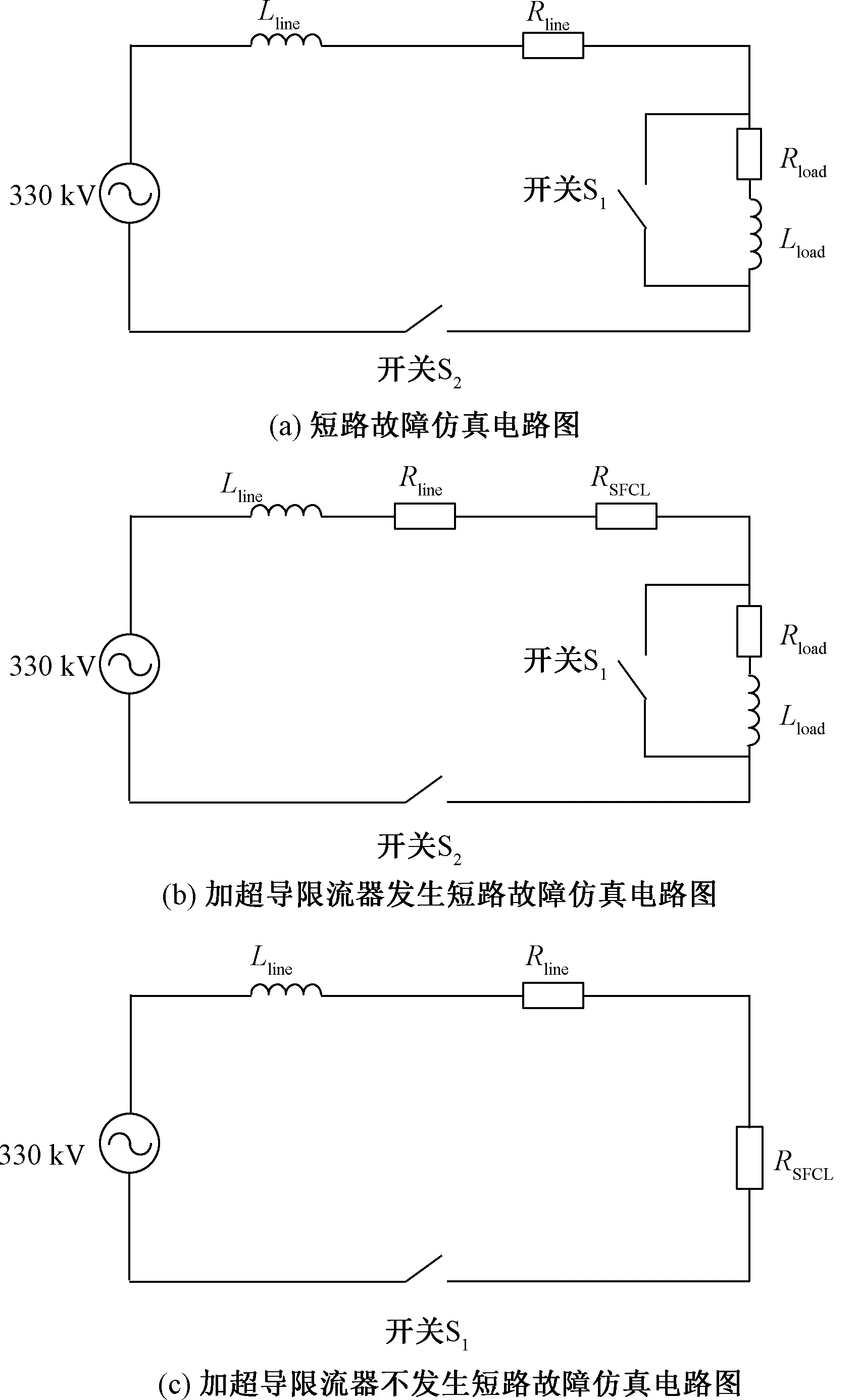
图1 仿真电路图Fig.1 Simulation circuit diagrams

2.2 超导限流器模型建立

常用的超导限流器模型有：时域模型、基于E-J特性曲线的物理模型、从实际短路故障中的电压、电流波形计算得到的电阻模型。

时域模型将失超电阻看作一个时变函数。一种典型的超导带材时域模型的函数如式(1)所示，表示短路故障发生后，超导带材从超导态过渡到失超态的时间内，电阻从0上升到RSC。

(1)

式中,RSC为失超电阻；TSC为时间常数。在该模型中RSC、TSC需要通过实验数据拟合[18,19]。

高温超导带材满足超导E-J特性曲线，在失超瞬间，超导失超电阻具有很强的非线性，上升速度快。基于E-J特性曲线建立的超导带材模型的实现方法为当实际电流I通过超导带材时，由E-J特性曲线计算出两端电压，再根据欧姆定律，求出此时的电阻R。一种典型超导带材物理模型的电阻变化函数如式(2)所示，电流密度J和温度T决定超导带材的电阻值RSFCL，一共分为三个阶段。

(2)

式中，Jc为临界电流密度；Tc为临界温度；n为超导体特征参数。

超导带材E-J对数曲线如图2所示，超导电阻的转换过程可以分为四个阶段：超导态、磁通蠕动阶段、磁通流动阶段和正常态。

图2 超导带材E-J对数曲线Fig.2 E-J log curve of superconducting tape

仿真时考虑断路器额定开断容量的情况，因为在额定容量，当系统还有较大直流分量时，断路器存在开断失败的风险。目前高压断路器的开断能力多为63 kA。仿真系统额定电压330 kV，短路电流峰值110 kA，有效值63 kA。由于该短路电流远大于超导带材的临界电流，超导带材迅速失超并且在直流分量衰减完毕之后的短路电流仍远大于超导带材的临界电流，因此通过E-J特性曲线计算出的失超电阻与时域模型表示的失超电阻基本一致。本文根据实验测得数据构造不同稳定失超阻值的失超曲线，使用时域电阻模型，避免了用复杂运算建立E-J特性曲线模型。

实验选美国超导公司(AMSC)的8602高温超导带材，带材具体参数如表1所示，测量超导带材失超电阻的实验电路如图3所示，图3中L=0.1 mH，C=100 mF，用高压探头测量超导带材两端电压，霍尔传感器测量流过带材的电流，根据带材电压与电流的比值获取失超电阻实验波形，测量结果如图4所示，用分段线性函数拟合实验失超电阻波形得到失超电阻拟合曲线。

表1 超导带材参数Tab.1 Superconducting tape parameters

图3 失超电阻测试电路图Fig.3 Quench resistance test circuit diagram

图4 8602带材失超特性曲线Fig.4 8602 tape measurement results

3 仿真结果

3.1 短路电流直流分量

仿真结果如图5所示，图5为发生短路故障时的短路电流全波形和交直流分量，对于直流时间常数为45 ms的330 kV交流系统，20 ms时发生短路，其短路电流峰值接近110 kA，起始直流分量为58 kA左右，衰减时间很长，在86.4 ms时衰减至12.6 kA(短路电流有效值的20%)。

图5 短路电流波形图Fig.5 Short-circuit current waveforms

3.2 不同超导阻值下的直流分量

选取电力系统标准时间常数45 ms，分别仿真了超导限流器稳定阻值为0 Ω、2.5 Ω、5 Ω、7.5 Ω、10 Ω、15 Ω、20 Ω、30 Ω时的短路电流和直流分量，获得不同阻值的超导限流器对短路电流和短路电流直流分量的抑制效果。

图6为不同阻值的超导限流器失超电阻R-T特性图，用时域电阻模型模拟，其中RSC、TSC根据实验测量数据拟合。以图4为例，0～1 ms时间内，电阻主要由超导带材的YBCO超导层决定，失超电阻变化率达到40 mΩ/(m·ms)。由高温超导的E-J特性可得，电流密度增加使超导内部电场强度呈幂指数增加，失超电阻迅速增大，增加的电阻值将会使超导带材产生更多热量，温度上升导致临界电流密度进一步减小，电场强度进一步扩大，从而形成正反馈。2 ms之后，超导进入完全失超状态，电阻主要取决于超导带材的不锈钢稳定层，形成第一个拐点。14 ms后，温度和电流密度对不锈钢的电阻率影响较小，电阻值增加缓慢。同时，在该时间段内，超导带材温度高于临界温度，超导产热和放趋于平衡，失超电阻上升率降低最后趋于平稳，形成第二个拐点，因此时域模型大多具有两个拐点。

图6 失超电阻R-T特性图Fig.6 R-T characteristic diagram of quench resistance

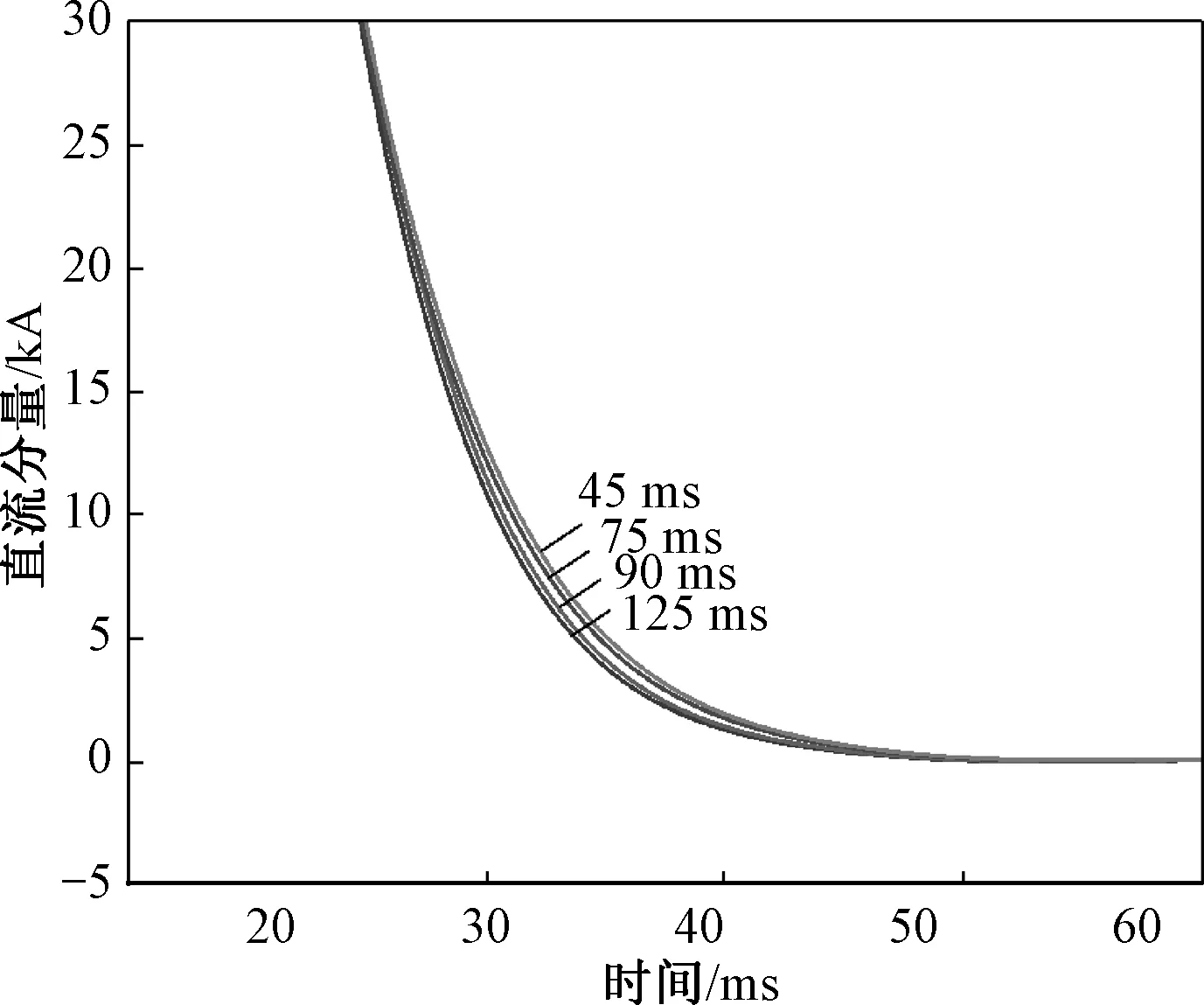
基于不同充电电流下超导失超电阻变化曲线建立的时域模型分段函数表达式为：R=at(0

表2 失超电阻表达式参数Tab.2 Parameters of quench resistance expressions

仿真结果如图7、图8所示。图7为失超电阻稳定值为0 Ω、2.5 Ω、5 Ω、7.5 Ω、10 Ω、15 Ω、20 Ω、30 Ω时的短路电流波形图。由于超导带材在短路故障发生时能自动反应，无需控制电路，响应时间极短，因此超导限流器能实现首半波限流，限流后短路电流峰值分别为110 kA、80.8 kA、63.7 kA、53.9 kA、44.4 kA、34.2 kA、27.2kA、19.6 kA，对短路电流峰值的抑制效果分别为0%、26.5%、42.1%、51%、59.6%、68.9%、75.3%、82.2%。

图7 不同失超电阻下短路电流波形图Fig.7 Short-circuit current waveforms of different quench resistances

图8是为失超电阻稳定值为0 Ω、2.5 Ω、5 Ω、7.5 Ω、10 Ω、15 Ω、20 Ω、30 Ω情况下的直流分量衰减趋势，加超导限流器后，直流分量均在60 ms内衰减完毕。稳定值为2.5 Ω的失超电阻，在34.9 ms将直流分量抑制到12.6 kA (短路电流有效值的20%)，稳定值≥5 Ω的失超电阻，在短路发生后10 ms之内将直流分量抑制到12.6 kA。

图8 不同失超电阻下直流分量衰减趋势Fig.8 DC component decaying trendency of different quench resistances

3.3 不同直流时间常数下的直流分量

根据3.2节的仿真结果，当超导限流器失超电阻为5 Ω时，就能在10 ms内将直流分量限制到断路器额定开断容量的20%，使断路器能可靠开断限制后的电流。因此，仿真设置超导限流器稳态阻值为5 Ω。《高压交流断路器》[20]中规定标准时间常数为 45 ms，特殊时间常数为 60 ms、75 ms、120 ms，因此仿真研究5 Ω的超导限流器阻值对4种直流时间常数的限制效果。4种时间常数下的电路阻抗参数见表3。

表3 不同直流时间常数下的电路参数Tab.3 Circuit parameters with different DC time constants

图9为4种时间常数下的直流分量衰减趋势。直流分量是由短路过程中感应电势和短路回路阻抗所确定的按指数规律衰减的电流，它的衰减速度由直流时间常数τ(τ=L/R)决定，τ越大，衰减越慢。仿真结果显示，在不同直流分量下，5 Ω的超导失超电阻值均在短路发生后10 ms之内就将直流分量限制到12.6 kA，断路器额定开断容量的20%。而且不同时间常数下，直流分量变化曲线差距较小，超导限流器具有很高的普适性，在不同时间常数下抑制效果相近。上述结论证明超导限流器的设计阻值能很好地满足不同时间常数的系统，具有良好适应性，同时也降低了超导限流器的设计难度。

图9 不同直流时间常数下直流分量衰减趋势Fig.9 DC component decaying trendency of different DC time constants

4 讨论

4.1 超导限流器失超阻值的优化设计方法

3.2节的结果表明，标准时间常数45 ms情况下，超导限流器对短路电流峰值和直流分量的抑制效果与阻值成正比。失超阻值对短路电流峰值抑制效果如图10所示。仿真结果显示，失超阻值和短路电流峰值抑制效果百分数的关系曲线斜率逐渐降低，因此低的失超电阻具有更高的性价比。超导失超电阻应同时满足对短路电流幅值和直流分量的抑制要求。超导限流器失超后呈现大电阻，能显著降低系统短路电流幅值，但增大失超电阻会使成本呈指数增加，因此，系统短路时，通常限流器对短路电流的限流深度达到30%～50% 即可满足需求，在该330 kV高压系统，超导阻值为3.5～7.5 Ω即满足要求。超导失超后的大电阻不仅显著降低了短路电流幅值，也使系统的直流分量衰减时间常数显著降低。阻值≥5 Ω的超导限流器，在短路发生后10 ms之内将直流分量抑制到12.6 kA(短路电流有效值的20%)，即满足了直流分量的抑制要求。综上所述，该系统超导限流器失超阻值优化设计为5 Ω。

图10 失超电阻对短路电流峰值抑制效果Fig.10 Quench resistance on short-circuit current peak suppression effect

4.2 超导限流器限流效果

对于直流时间常数τ=L/R，不加超导限流器发生短路时，直流分量衰减时间不同，需根据情况设置断路器的分闸时间。3.3节的结果表明，当超导限流器失超电阻为5 Ω时，标准时间常数45 ms和特殊时间常数 60 ms、75 ms、120 ms情况下，线路短路电阻仅占超导限流器失超阻值的5%～10%，因此，时间常数为45～120 ms时，使系统安装超导限流器后的时间常数τ相差小于10%，在不同时间常数下，超导限流器的限流效果相差小于10%。因此，超导限流器适用于不同工况下的短路故障，且无需更改断路器的分闸时间，降低了系统超导限流器和保护设备的设计难度和分散性，拓宽了利用超导限流器抑制系统直流分量的适用范围。

5 结论

现有超导直流限流器设计方法主要考虑限流深度和限流速度，往往需要具有60% 甚至以上的限流深度以及限制短路电流快速增长的能力。而在交流系统中，由于有自然过零点的存在，对限流深度的要求有所降低，往往达到30%～50% 即可，本文在此基础上更加注重对直流分量和直流分量时间常数的考虑，以一定时间内对直流分量的限流效果和对直流时间常数的改善作为评判标准来选择合适阻值的超导限流器。提出使用超导限流器在限制短路电流幅值的同时，抑制短路电流直流分量的方法，仿真结果表明超导限流器对直流分量的抑制效果非常明显，且适用于不同工况下的短路故障，同时为超导故障限流器失超阻值的选取提供了理论依据。

具体结论如下：

(1)标准时间常数45 ms下，超导限流器对短路电流峰值和直流分量的抑制效果与阻值成正比，可从对短路电流和直流分量的抑制效果两方面为超导限流器阻值的选取提供判据。

(2)文中330 kV高压系统选取阻值为5 Ω的超导限流器，限流深度达到40%，短路发生后10 ms之内将直流分量抑制到短路电流有效值的20%。

(3)标准时间常数 45 ms和特殊时间常数60 ms、75 ms、120 ms 4种工况下，超导限流器均可适用，且无需更改断路器分闸时间，降低了保护系统设计难度，设计的超导限流器具有良好的普适性。