基于内部能量管理和外部路径规划协同的水下无人航行器能耗优化

2021-11-02陈洋洋谢长君吴细秀范则阳

电工电能新技术 2021年10期

侯慧，陈洋洋，谢长君，吴细秀，谢坤，范则阳

(1.武汉理工大学自动化学院，湖北武汉 430070； 2.中国舰船研究设计中心，湖北武汉 430064)

1 引言

随着世界各国对海洋资源开发与利用的日益重视，水下无人航行器(Unmanned Underwater Vehicle, UUV)因具有自主航行能力，可以代替人类执行众多危险任务，已经成为海洋领域研究的一大热点[1,2]。但UUV自身体积有限，能够携带的能源储量也有限，因此如何以最小的能耗代价来完成较长航程任务是一个亟待解决的研究课题[3]。

在不改变UUV本身结构的前提下，可以通过制定能量管理策略[4]和规划UUV的航行路径[5]减少能源消耗。能量管理策略大致可分为基于规则控制和基于优化控制等[6]。基于规则控制的能量管理策略由于实用性强、可靠性高等优势在实际生产中应用较为广泛[7]。其中，基于确定规则，文献[8]对功率跟随能量管理策略中的参数和荷电状态(State Of Charge, SOC)调节方式进行了充分分析，设计了Z曲线法和PI调节法，使能量源的SOC上限和充电功率参数保持在适度范围内，以减小能量源的燃料消耗量和波动率。相对于确定规则控制，模糊规则控制是将输入量进行模糊化处理，经过模糊规则推理计算出输出量，不需要建立被控对象的确切数学模型[9]。文献[10]使用IF-THEN规则列表将不同能量源相关联，并基于系统不同驱动模式为它们分配一定的逻辑关系，实现不同能量源之间的功率分配，从而提高系统的整体燃料经济性。但基于规则控制的能量管理策略由于其预先设定了规则，在实际应用过程中无法进行调整，因此导致在复杂的工况下控制效果表现欠佳，而基于优化控制的能量管理策略则可以在复杂工况下寻求系统的最优解[11]。

基于优化控制的能量管理策略主要分为全局最优和瞬时最优等[12]。为获得全局最优，文献[13]将动态规划算法和模糊控制策略进行结合，动态规划算法应用于各能量源之间的最优功率分配，并将其结果用于模糊控制策略的设计，以获得整个循环工况的最小燃料消耗。而文献[14]基于庞特里亚金瞬时最小值原理，通过在管理层加入在线识别层，利用自适应递推最小二乘法在线辨识模型跟踪能量源性能的变化，使其时刻运行在最佳性能从而减小系统的燃料消耗。虽然全局最优能量管理策略需要预知系统的循环工况，计算量大，存在“维数灾难”的可能性，但其可以保证经济性的全局最优[15]。

也有一些学者另辟蹊径，通过规划UUV的航行路径减少其能源消耗。文献[16]以节能为目标，采用基于遗传算法的动态规划完成路径规划，验证了可以通过规划航行路径减少UUV的能耗，但其并没有考虑到海洋环境，在路径规划中忽视环境影响，可能会使UUV航行在强流中导致能源浪费，而且会增加撞击障碍物的潜在危险性。文献[17]利用多重粘性兰姆涡和二维Navier-Stokes方程模拟了海洋水环境，并通过结构差分进化算法获得了更高的航行速度，从而显著地节省了能源消耗。文献[18]提出了一种以环形边界作为安全距离约束的A*方法，解决了UUV在海洋水环境中的运动规划问题，同时探讨了在部分环境中，不同强度的逆流和顺流分别顺时针和逆时针方向移动对最优航行路径的影响。

综上所述，现有对于UUV能耗优化的研究要么集中于制定能量管理策略，要么集中于规划UUV的航行路径，但使用能量管理策略会得出一个最优速度、一个最优动力供给方案，使用路径规划又会得出另一个最优速度、另一个最优动力供给方案，然而UUV只能以一个速度、一个动力供给方案航行，必然需要将两者统一。目前，将两者结合的研究较少，同时也缺乏考虑利用海流的流场减少UUV的出力从而减少其能源消耗。本文将内部能量管理策略和外部路径规划结合在一起，通过优化UUV的航速和分配2套燃料电堆和蓄电池的输出功率，同时选择搭乘海流的切入点和切出点，使得UUV在起始点之间航行需要的等效氢耗最小。

2 UUV混合动力系统拓扑结构

UUV混合动力系统拓扑结构如图1所示，主要包括2套燃料电堆、1套蓄电池、主网、推进电机以及辅机设备等。燃料电堆与蓄电池通过与主网相连接为推进电机和各种辅机设备供电。

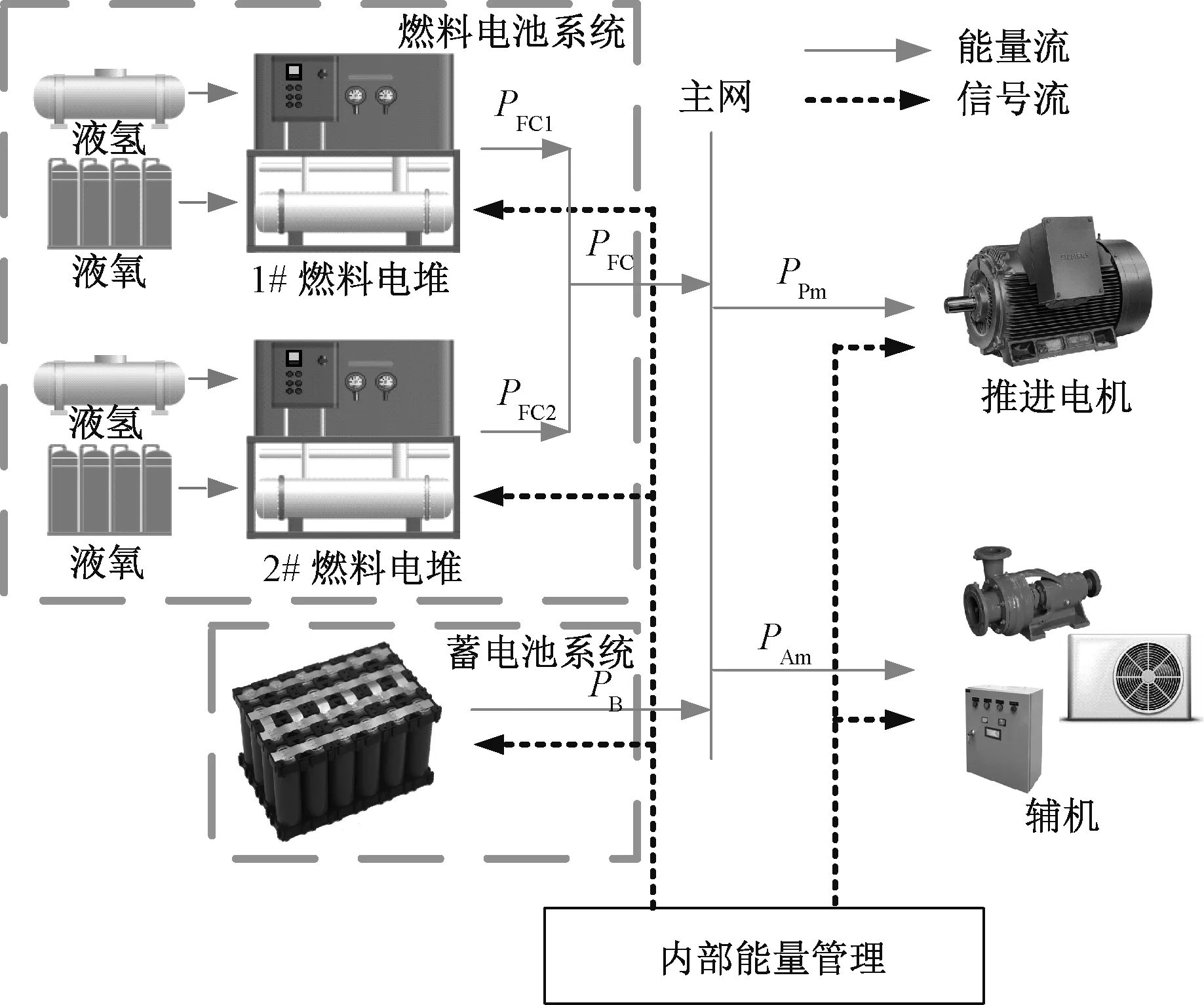
图1 UUV混合动力系统拓扑结构图Fig.1 Topology of UUV hybrid power system

UUV通过合理调节燃料电堆之间的输出功率、燃料电池系统和蓄电池系统之间的输出功率实现UUV混合动力系统的能量管理，并通过调节推进电机的功率调节UUV的航速。PFC、PB、PPm、PAm之间的关系满足：

PFC+PB=PPm+PAm

(1)

式中，PFC为燃料电池系统的输出功率；PB为蓄电池系统的输出功率；PPm为推进电机的需求功率；PAm为UUV各种辅机设备所需总功率。

3 基于内部能量管理和外部路径规划协同的UUV能耗优化架构

内部能量管理为UUV输出不同航速下的需求功率，UUV在不同外部水流环境下有不同的需求功率，故内部能量管理和外部路径规划之间必然存在相互影响，本文将UUV的内外层优化置于统一的框架内，以航速为耦合变量，建立基于内部能量管理和外部路径规划的能耗优化模型，以UUV在起始点之间航行需要的等效氢耗最小为目标，求解UUV的最佳航行路径、航速和功率分配供给方案。其中，内部能量管理层根据等效氢耗理论，在水下无人航行器不同需求功率下，使用模拟退火混合遗传算法为2套燃料电堆和蓄电池分配输出功率，使得UUV混合动力系统的等效氢耗最小；外部路径规划层使用A*算法[19]选择搭乘海流的切入点和切出点，使水下无人航行器能够充分利用海流的流场。其优化架构如图2所示。

图2 基于内部能量管理和外部路径规划协同的UUV能耗优化架构Fig.2 Energy consumption optimization architecture of UUV based on internal energy management and external path planning

4 UUV能耗优化模型

4.1 第一级优化

(1)目标函数

以燃料电池系统的瞬时氢耗最小为优化目标，在燃料电池系统不同输出功率下，优化分配两套燃料电堆之间的输出功率。即：

(2)

式中，PFC为燃料电池系统的输出功率；CFC(PFC)为燃料电池系统的输出功率为PFC时，燃料电池系统的瞬时氢耗；PFCi为第i台燃料电堆的输出功率；cFC(PFCi)为第i台燃料电堆的输出功率为PFCi时，第i台燃料电堆的瞬时氢耗[20]。

此时，燃料电池系统输出功率PFC与各燃料电堆输出功率PFCi之间的关系满足：

(3)

式中，UFCi为第i台燃料电堆的运行状态，取1时，表示燃料电堆运行，取0时表示燃料电池电堆停机。

(2)约束条件

各燃料电堆的输出功率应位于各燃料电堆输出功率可达范围内，可表示为：

PFCimin≤PFCi≤PFCimax或PFCi=0i=1,2

(4)

式中，PFCimax、PFCimin分别为第i套燃料电堆输出功率的最大值、最小值。

4.2 第二级优化

(1)目标函数

在燃料电池系统供电时，为了使得在相同输出功率下燃料电池系统的瞬时氢耗最小，两台燃料电堆之间的功率分配使用第一级优化的功率分配方案。并在此基础上，以UUV混合动力系统的等效瞬时氢耗最小为优化目标，在不同航速下，优化分配燃料电池系统和蓄电池系统之间的输出功率。即：

minCHPS(v)=CFC(PFC)+CB(PB)

(5)

此时

PB+PFC=fPm(v)+PAm

(6)

式中，CHPS(v)为UUV的航速为v时，UUV混合动力系统的等效瞬时氢耗；CB(PB)为蓄电池系统的输出功率为PB时，蓄电池系统的等效瞬时氢耗；fPm(v)为UUV的航速为v时，推进电机所需功率[21]。

本文是依据等效氢耗理论，将蓄电池系统的耗电量转换为对应的液氢质量，以便用于UUV混合动力系统的燃料经济性分析。根据文献[22，23]所述，蓄电池系统瞬时氢耗等效为：

(7)

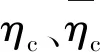
(2)约束条件

1)蓄电池系统出力约束

蓄电池系统的输出功率应位于蓄电池系统输出功率的可达范围内，可表示为：

PBmin≤PB≤PBmax或PB=0

(8)

式中，PBmax、PBmin分别为蓄电池系统输出功率的最大值、最小值。

2)燃料电池系统出力约束

燃料电池系统的输出功率应位于燃料电池系统输出功率的可达范围内，可表示为：

PFCmin≤PFC≤PFCmax或PFC=0

(9)

式中，PFCmax、PFCmin分别为燃料电池系统输出功率的最大值、最小值。

4.3 第三级优化

(1)目标函数

在UUV混合动力系统供电时，为了使得在相同航速下混合动力系统的等效瞬时氢耗最小，燃料电池系统和蓄电池系统之间的功率分配使用第二级优化的功率分配方案。并在此基础上，以UUV在起始点之间航行需要的等效氢耗最小为优化目标，在不同航速下，规划UUV的航行路径。即：

(10)

式中，C为UUV在起始点之间航行需要的等效氢耗；(i0,j0)为UUV当前时刻所在的经纬度；(i,j)为UUV下一个时刻所在的经纬度；SF为UUV的可行点集合；C(i0,j0)→(i,j)为UUV从(i0,j0)到(i,j)所需要消耗的液氢质量，可表示为：

C(i0,j0)→(i,j)=r(i0,j0)→(i,j)·t(i0,j0)→(i,j)

(11)

式中，t(i0,j0)→(i,j)为UUV从(i0,j0)到(i,j)所需要的时间；r(i0,j0)→(i,j)为UUV从(i0,j0)到(i,j)期间时，UUV的瞬时氢耗率，可表示为：

r(i0,j0)→(i,j)=CHPS(v(i0,j0)→(i,j))

(12)

式中，v(i0,j0)→(i,j)为UUV从(i0,j0)到(i,j)期间时，UUV的航速。

UUV航行于有水流速度的水域时，一般认为水流对船舶运动的影响仅属于运动学上的范畴，只引起船舶运动上的漂移，可表示为：

v=vg+vc

(13)

式中，v为UUV相对于陆地的航速；vg为UUV相对于水流的航速；vc为水流速度。

(14)

式中，d(i0,j0)→(i,j)为UUV从(i0,j0)到(i,j)之间的距离。

(2)约束条件

UUV在航行时，航速应约束在一定范围内。

vmin≤v≤vmax

(15)

式中，vmax、vmin为UUV航行时航速的最大值、最小值。

4.4 优化求解流程

(1)内部能量管理层

在内部能量管理层，本文使用模拟退火混合遗传算法。模拟退火混合遗传算法是将遗传算法与模拟退火算法相结合的一种混合全局搜索算法。遗传算法的局部搜索能力较差，但把握总体搜索过程的能力较强；而模拟退火算法具有较强的局部搜索能力，并能在搜索过程中避免陷于局部最优解[24]。本文将模拟退火算法和遗传算法相结合，取长补短，以获得更好的全局搜索能力。

(2)外部路径规划层

在外部路径规划层，本文使用A*算法。搜索算法大致可分为深度搜索和广度搜索等。深度搜索的优点是搜索速度快、时间短，但是不一定能求出最优解；而广度搜索优点是可以保证求出最优解，但由于其是一层层搜索，必须扩展每一个点，所以缺乏时间效率和空间效率。而A*算法将两者结合，取长补短，既有极大概率求出最优解，又可以减少冗余时间[19]。

本文基于内部能量管理和外部路径规划协同的水下无人航行器能耗优化求解流程图如图3所示。

5 算例分析

5.1 内部能量管理层优化分析

(1)第一级优化分析

考虑燃料电池系统内部各电堆之间的功率分配策略，本文比较了2种方案。

方案1：基于规则控制，当PFC≤PFCimax时，只需一套燃料电堆运行。当PFCimax≤PFC≤2PFCimax时，一套电堆全功率运行，另一套燃料电堆承担剩余负荷功率。

方案2：基于优化控制，使用模拟退火混合遗传算法优化分配两套燃料电堆之间的输出功率。

方案1为方案2的对比方案。2种方案的瞬时氢耗优化结果如图4所示。

由图4可知，方案2优于方案1，在相同输出功率下，最大可减少10.72%瞬时氢耗。和方案2相比，方案1虽然可以减少燃料电堆的启停次数，但增加了燃料电池系统的瞬时氢耗，故在第二、三级优化分析中，不同燃料电池系统输出功率下，两套燃料电堆之间的功率分配采用方案2，具体功率分配如图5所示。

由图5可知，模拟退火混合遗传算法优化分配燃料电池系统输出功率的结果为2套燃料电堆各承担燃料电池系统输出功率的一半。

(2)第二级优化分析

考虑UUV混合动力系统内燃料电池系统和蓄电池系统之间的功率分配策略，本文比较了3种方案。

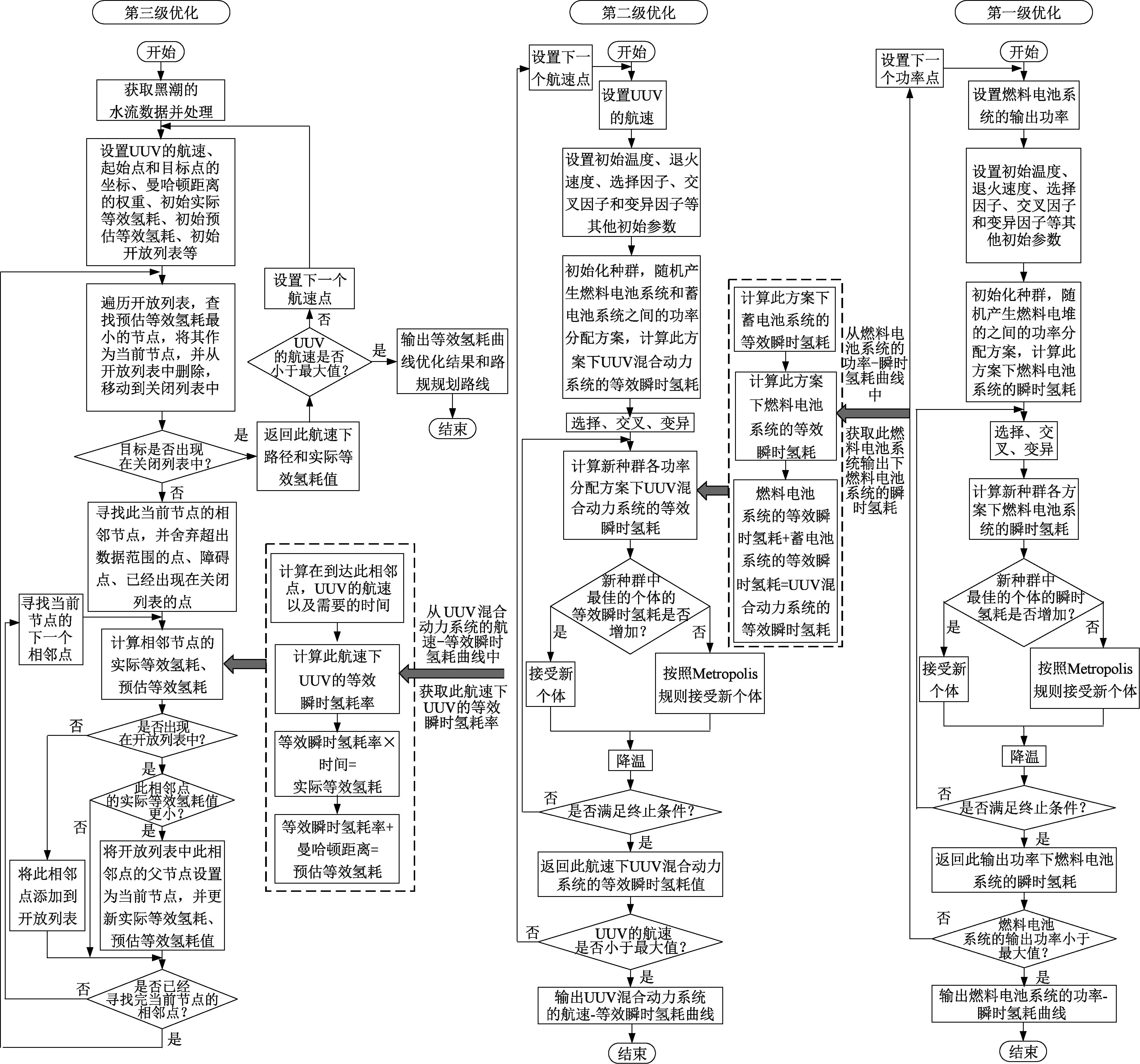
图3 优化求解流程图Fig.3 Flow chart of optimization solution

方案3：基于单能源，蓄电池系统单独运行。

方案4：基于多能源规则控制，当UUV混合动力系统输出功率小于等于4PFCimax时，燃料电池系统和蓄电池系统平均分配UUV混合动力系统输出功率；当UUV混合动力系统输出功率大于4PFCimax时，燃料电池系统全功率运行，蓄电池系统承担剩余功率。

方案5：基于多能源优化控制，使用模拟退火混合遗传算法优化分配燃料电池系统和蓄电池系统之间的输出功率。

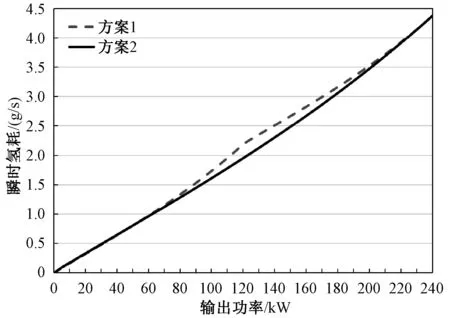
图4 方案1和方案2的瞬时氢耗优化结果Fig.4 Optimization results of instantaneous hydrogen consumption in plan 1 and 2

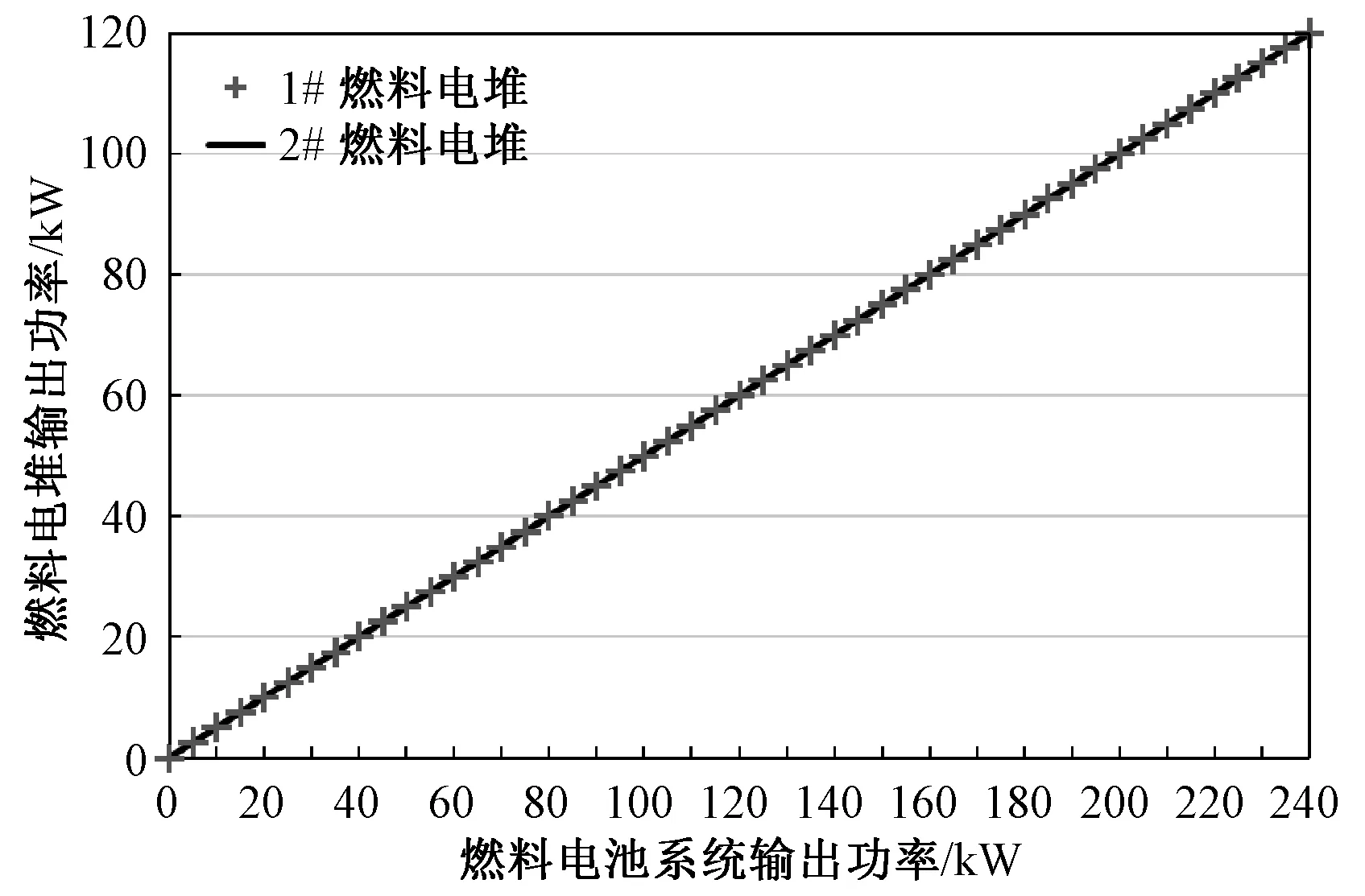
图5 各燃料电堆在不同燃料电池系统的输出功率下的出力曲线Fig.5 Output curves of each fuel electric reactor at different fuel cell systems output power

方案3、方案4均为方案5的对比方案。3种方案的等效瞬时氢耗优化结果如图6所示。

图6 方案3～方案5的等效瞬时氢耗优化结果Fig.6 Optimization results of equivalent instantaneous hydrogen consumption in plan 3～5

由图6可知，方案4和方案5优于方案3，表明燃料电池系统和蓄电池系统共同供电比蓄电池系统单独供电可以很大程度上减少UUV混合动力系统的等效瞬时氢耗。同时，方案5优于方案4，表明使用模拟退火混合遗传算法优化分配燃料电池系统和蓄电池系统之间的输出功率优于燃料电池系统和蓄电池系统平均分配UUV混合动力系统输出功率，故在第三级优化分析中，不同航速下，燃料电池系统和蓄电池系统之间的功率分配采用方案5，具体功率分配如图7所示。

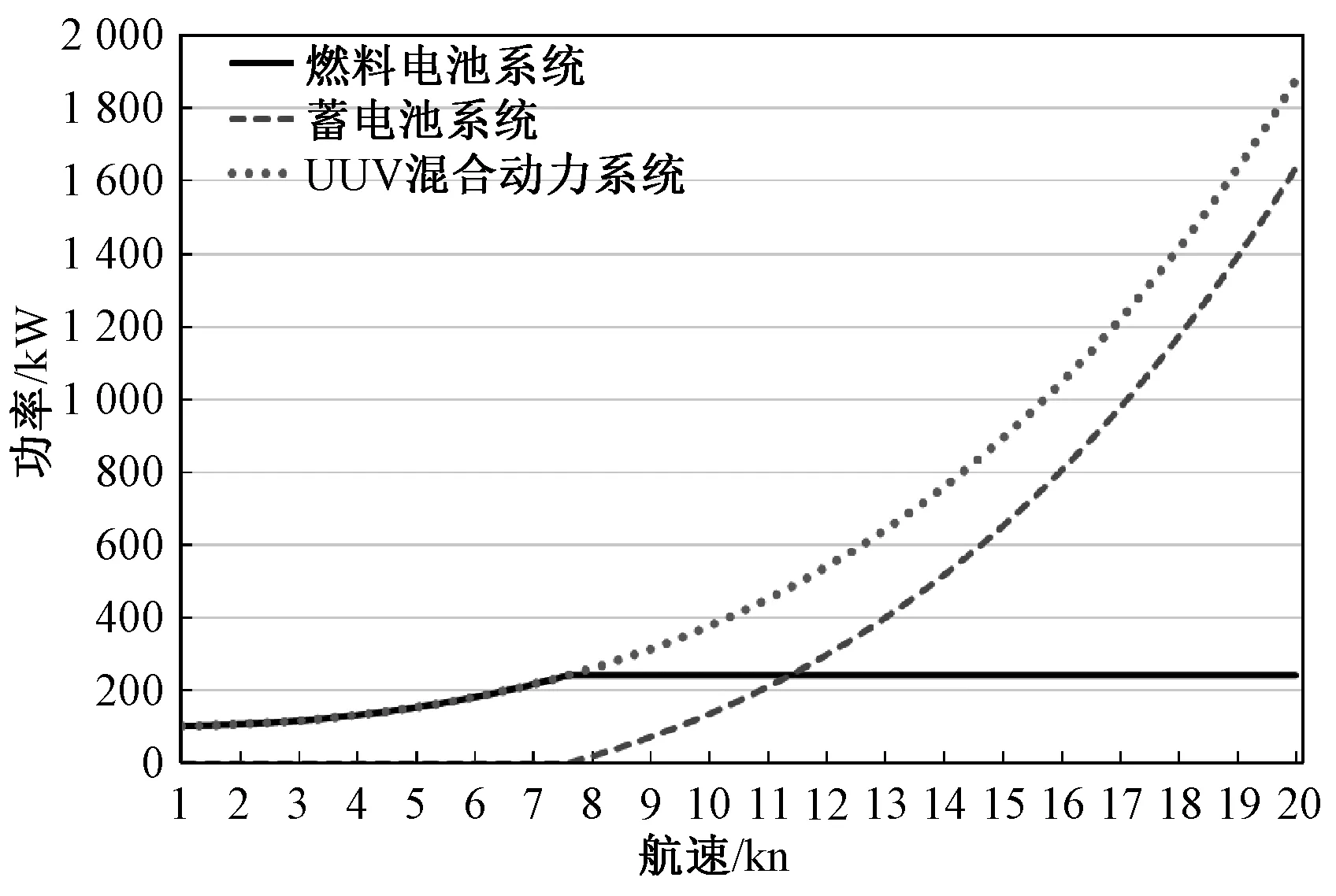
图7 各系统在不同航速下的出力曲线Fig.7 Output curve of each system at different speeds

由图7可知，当UUV航行在中低速(即1～11 kn附近)范围时，UUV主要由燃料电池系统供电，当UUV航行在高速范围时，燃料电池系统全功率运行，蓄电池系统承担剩余负荷功率。

5.2 外部路径规划层优化分析

忽视海洋水环境影响，单独考虑UUV是没有实际意义的[17]。考虑海流及障碍物，本文从国家海洋科学数据中心截取了(32.5°N，140.375°E)到(41.25°N，149.125°E)部分的黑潮数据[25]，采用直角坐标系对海洋水环境进行建模，充分利用栅格化建模的优点，使路径简单明了、易于实现，如图8所示。

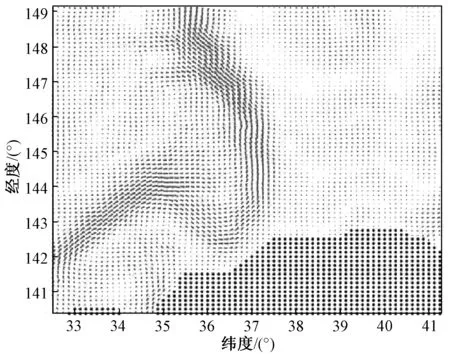
图8 二维水环境地图建模示意图Fig.8 Schematic diagram of two-dimensional water environment map model

为了对比和分析内部能量管理和外部路径规划对UUV在起始点之间航行需要的等效氢耗和最优路径的影响，设置了4种不同的优化方案，分别为：无优化，UUV由蓄电池系统单独供电且选择直达路线；单独使用外部路径规划层，且UUV由蓄电池系统单独供电；单独使用内部能量管理层，且UUV选择直达路线；内部能量管理和外部路径规划协同优化。

(1)单独路径规划优化分析

由蓄电池系统单独供电，从(32.5°N，140.375°E)出发到(41.25°N，149.125°E)，UUV在不同航速下选择直达路线和路径规划路线所需要的等效氢耗如图9所示。

图9 直达路线和路径规划路线下UUV在起始点之间航行需要的等效氢耗曲线Fig.9 Equivalent hydrogen consumption curves required for UUV to voyage between the start and end points under the direct route and route planning route

由图9可知，由蓄电池系统单独供电，直达路线下，当UUV的航速为11.3 kn时，UUV在起始点之间航行需要的等效氢耗最小为881.69 kg；路径规划路线下，当UUV的航速为11.6 kn时，在起始点之间航行需要的等效氢耗最小为868.06 kg。只考虑路径规划，UUV可节省1.55%等效氢耗量；当UUV航行在17.1 kn时，等效氢耗减少量最大为2.31%。

为使得UUV能够充分利用黑潮的流场，由A*算法选择搭乘黑潮的切入点和切出点，其规划路线如图10所示。

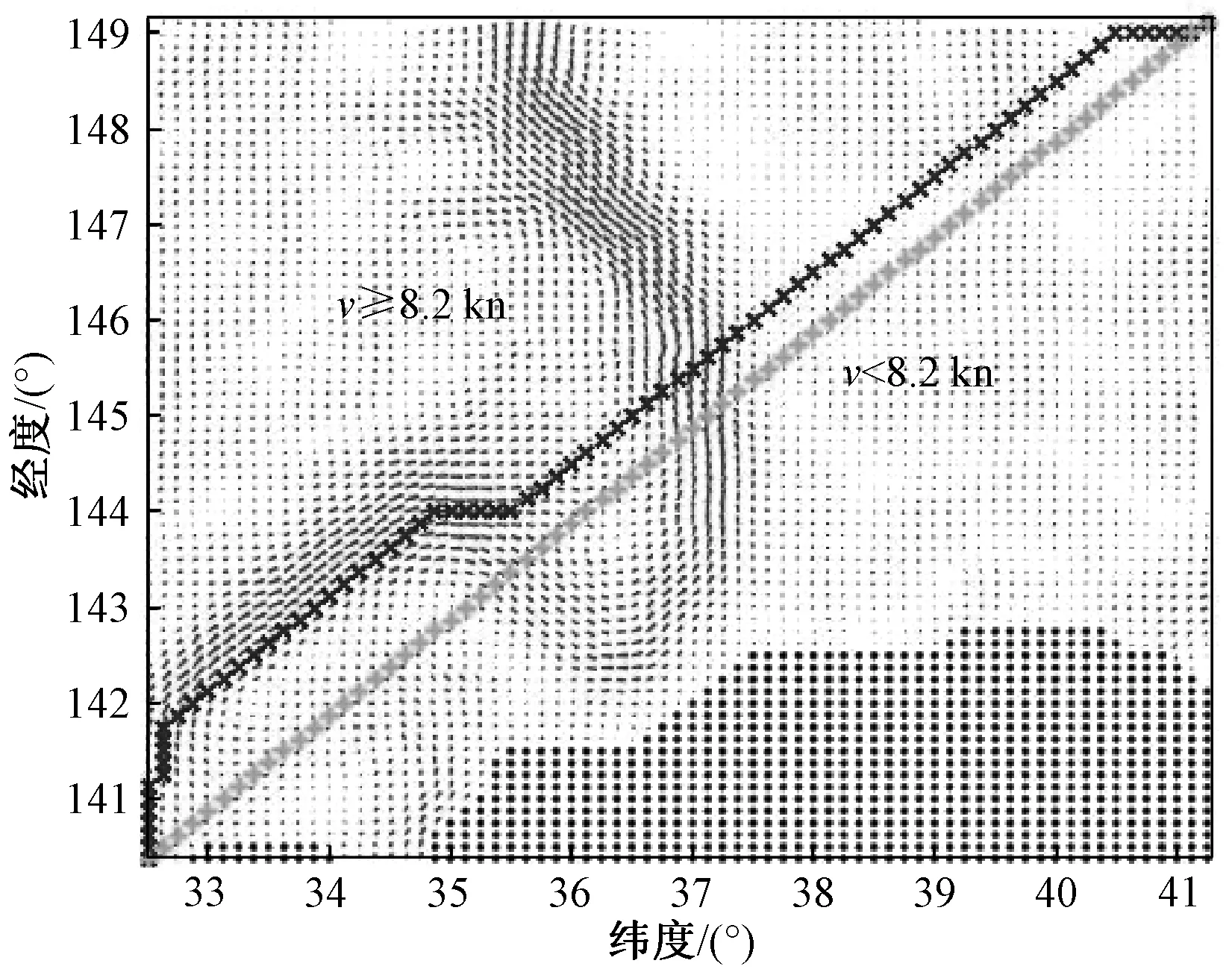
图10 不同航速下的路径规划路线图Fig.10 Path planning roadmap at different speeds.

由图10所知，当v≥8.2 kn时，为了获得更小的等效氢耗，UUV选择绕路搭乘黑潮的前半部分；当v<8.2 kn时，UUV并没有选择搭乘黑潮，而是选择直达路线。其原因为：UUV选择搭乘黑潮，会由于绕路而增加UUV的路程，从而增加UUV在起始点之间航行需要的等效氢耗；UUV搭乘黑潮，会由于黑潮带来的相对速度，从而减少UUV在起始点之间航行需要的等效氢耗；故当搭乘黑潮带来的等效氢耗减少量小于绕路带来的等效氢耗增加量时，UUV会选择搭乘黑潮，否则，选择直达路线。

(2)单独能量管理优化分析

由燃料电池系统和蓄电池系统共同供电，从(32.5°N，140.375°E)出发到(41.25°N，149.125°E)，UUV在不同航速下基于多能源优化控制的方案5和基于蓄电池系统单独运行的方案3选择直达路线所需要的等效氢耗如图11所示。

图11 基于多能源优化控制和基于蓄电池系统单独运行时UUV在起始点之间航行需要的等效氢耗曲线Fig.11 Equivalent hydrogen consumption curves required for UUV to voyage between the start and end points based on multi-energy optimization control and based on battery system running separately at different speeds

由图11可知，基于多能源优化控制的方案5在直达路线下，当UUV的航速为10.0 kn时，其在起始点之间航行需要的等效氢耗最小为631.03 kg，比基于蓄电池系统单独运行的方案3在直达路线下，所需等效氢耗量减少了28.43%。

(3)内部能量管理和外部路径规划协同优化分析

UUV从(32.5°N，140.375°E)出发到(41.25°N，149.125°E)，在不同航速下，基于内部能量管理和外部路径规划协同优化下的等效氢耗曲线如图12所示。

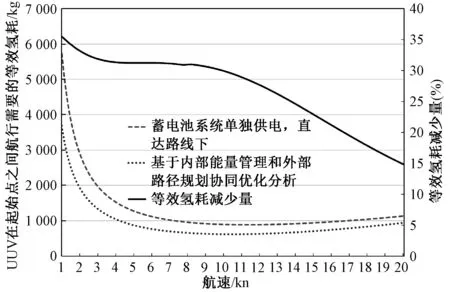
图12 基于内部能量管理和外部路径规划协同优化UUV在起始点之间航行需要的等效氢耗曲线Fig.12 Equivalent hydrogen consumption curves required for UUV to voyage between the start and end points based on internal energy management and external path planning

由图12可知，基于内部能量管理和外部路径规划协同优化下，当UUV的航速为10.5 kn时，其在起始点之间航行需要的等效氢耗最小为616.50 kg，比蓄电池系统单独供电在直达路径下减少了30.08%的所需等效氢耗量。其规划路线如图13所示。

图13 基于内部能量管理和外部路径规划协同优化的在不同航速下的规划路线Fig.13 Planning routes at different speeds based on internal energy management and external path planning

由图13所知，当v≥7.8 kn时，为了获得更小的等效氢耗，UUV选择绕路搭乘黑潮的前半部分；当v<7.8 kn时，UUV选择直达路线。对比图10和图13可知，内部能量管理方案5通过减少相同航速下UUV混合动力系统的等效瞬时氢耗，从而减小UUV选择绕路搭乘黑潮的起始速度。同时，在不同航速范围内，UUV选择绕路搭乘黑潮的路径也不尽相同。

5.3 不同优化策略下的最小等效氢耗对比

由图10～图13可知，不同优化策略下的最小等效氢耗如表1所示。

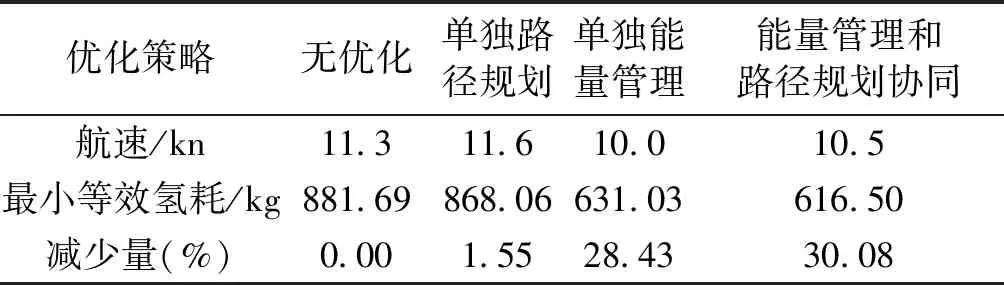
表1 不同优化策略下的最小等效氢耗Tab.1 Minimum equivalent hydrogen consumption at different optimization strategies

由表1可知，当UUV航行在11.6 kn时，单独路径规划下，其在起始点之间航行需要的等效氢耗最小，但单独能量管理策略优化下的等效氢耗并不是最小，说明能量管理和路径规划并不是通过简单地相加就可以使UUV在起始点之间航行需要的等效氢耗更小，它们之间存在耦合关系。相比单独能量管理优化和单独路径规划，能量管理和路径规划协同优化能够更大程度地减少UUV在起始点之间航行需要的最小等效氢耗。