基于能效的交直流混合配电母线配置方法研究

2021-11-02朱梦颖彭勇刚宋弘亮

电工电能新技术 2021年10期

朱梦颖，彭勇刚，宋弘亮

(1.浙江大学电气工程学院，浙江杭州 310027； 2.宁波市电力设计院有限公司，浙江宁波 315000)

1 引言

随着分布式电源接入比例不断增加[1]、电力电子技术和控制技术飞速发展，直流配电系统逐渐走入人们的视野[2]。由于直流系统便于可再生能源、储能装置、充电桩等新能源设备的互动化接入；相对交流配电网络而言，在电能质量、供电可靠性、供电能力等方面均具有一定优势；并且符合当前国网公司发展基于信息物理融合的能源互联网和电力物联网的需求[2,3]，国内外团队相继从各角度开展针对交直流混合配电网的研究。

在系统评估方面，文献[4-8]分别针对交直流方案、系统建立不同方面的评估指标体系，对交直流系统进行评价。文献[9]研究并提出了直流电压等级选择对直流系统能效的影响。在优化方面，文献[10-15]分别从设备的需求侧响应、光储联合、电力电子变压器等方面开展交直流混合电网优化运行调度的研究；文献[16,17]从交直流混合主动配电网的分层分布式的优化形式和考虑柔性负荷两方面对交直流混合系统优化进行创新。在应用方面，有团队从直流配电网关键设备特性、运行控制、负荷接入方式和网络拓扑结构等方面出发，研究交直流混合电网的适用模式[1,18,19]；也有团队从分布式能源接入和工程出发在供电效率、可靠性、电能质量等方面论证交直流配电系统相对纯交流配电系统的优势[20]。

国外，美国弗吉尼亚理工大学电力电子系统应用中心提出了交流母线主要用于负荷供电，直流母线用于接入分布式电源和分布式储能，交直流母线共存的交直流配电分层连接的混合配电结构[21]。美国北卡罗莱纳大学提出了未来可再生电力能源传输与管理系统结构和能量路由器的概念[22]。英国、瑞士及意大利等国也开展了通过新型功率变换技术适应未来有大量分布式电源接入的欧洲电网的功率流动管理技术的研究。以上研究均对交直流混合系统的发展具有较大价值，但是并没有考虑母线源-荷-储配置对设置交直流母线时是否具有能效优势的影响。

国内交直流配电网研究中，在配电系统能效方面的研究多注重对系统整体能效进行评估，以证明直流系统优于交流系统或评价体系和指标构建，对实际系统的评价和高压直流系统的规划有一定的借鉴意义，但是对于实际低压交直流配电网工程设计和配置参考价值有限。文献[23]针对商业楼宇的负荷性质进行分析，通过商业楼宇实际工程时序数据对交直流配电系统进行建模和能效对比，同时分析交直流系统各部分的全年损耗占比，证明了交直流系统在能效方面存在优势。对实际应用有一定参考价值，但是对负荷特性有一定限制，没有考虑光伏容量与负荷容量比例，储能方面也未考虑最大充放电功率的影响。

目前电力系统中可再生能源、储能装置、充电桩等新能源设备比重加大，广义上直流负荷逐渐增加，相对传统交流配电系统而言，直流配电系统优势日益明显。随着交直流配电系统应用范围逐渐扩大，在实际配电工程规划设计阶段，如何选择母线类型、怎样进行母线配置、如何确定系统结构等问题将逐渐显现。如今交直流系统研究已经取得了一定的成果，然而在实际交直流系统规划配置阶段，如何选择和配置交直流母线以提升系统能效、如何规划交直流系统结构使其更具能效优势还没有明确界限。本文针对交直流配电网络各元件特性，对交直流混合系统各类型元件建立能效数学模型，对母线组合为纯负载、负载-光伏、负载-光伏-储能三种典型场景；基于典型日曲线，考虑瞬时和日周期两种场景；对于以上时间维度和组合维度的各种组合场景，层层递进，进行各种情景下交、直流母线能效对比，对各种组合场景下，交直流母线如何配置才具有能效优势进行探讨。为交直流母线规划设计阶段的配置问题提供一定的理论依据。

2 研究原理和建模

2.1 交直流母线各元器件能效数学建模

(1)电力电子元件

由于电力电子变压器简化模型由三个电压源型逆变器(Voltage Source Converter,VSC)元件组成，因此仅需对VSC建立能效数学模型，考虑只需计算元件能耗，根据文献[24]，对于VSC换流器损耗率建立数学模型如下：

(1)

式中，η为换流器损耗率；γ为换流器实际功率与额定功率的比值(负载率)。

(2)储能元件

储能元件在配电网络损耗计算中，忽略装置的老化，总共需要考虑三个方面损耗：充电损耗、放电损耗、自放电损耗。储能装置能效数学模型如式(2)、式(3)所示，其中充放电损耗如下：

PLoss_Sto=|PStorageλ|

(2)

式中，PLoss_Sto为储能损耗；PStorage为储能充放电功率；λ为储能充放电损耗率。

自放电损耗基于时间维度，根据目前市场标称参数，借鉴参考文献[24]，储能自放电损耗按每月3%比例，均分至每5 min计算漏电率，其数学模型为：

(3)

式中，WLoss_Ts为T时间内的功率损耗;SOCi_Storage为第i时间段初期，储能装置荷电状态；ε为漏电率；N为划分时段的总数。

(3)负荷和光伏元件

在瞬时维度，对于负荷能效模型，交流、直流负荷装机容量为SAC、SDC，负荷利用系数γL表示负荷实际用电占装机容量比例，实际用电为：

PLoad=PAC+PDC=SACγL+SDCγL

(4)

对于光伏能效模型，装机容量为SPV，光伏出力系数为γPV，其实际出力功率如下：

PPV=SPVγPV

(5)

式中，PLoad为总负荷实际用电量；PAC为交流负荷的实际用电量；PDC为直流负荷的实际用电量；PPV为光伏的实际出力。

在时间维度，以江苏某项目一年数据处理和抽象所得的典型日负荷和日光伏曲线数据(采样间隔统一为5 min)，作为本文研究典型日负荷情况下的负荷和光伏计算用数学模型。

2.2 研究方法

本文针对交直流配电系统的设计阶段，从单母线配置开始，在考虑纯负载、负载-光伏、负载-光伏-储能从简到繁三种典型场景下，基于典型日曲线，以直流负荷占比为因变量，从瞬时递进到日周期，对交、直流母线如何选择和配置时母线具有能效方面优势、交直流母线能效优势转换点随各变量变化的情况，进行一定程度的研究和探讨。最后采用实际工程的拓扑结构和典型日曲线对研究结果进行验证，同时验证了项目系统拓扑相对传统交直流系统拓扑具有能效优势，为交直流配电系统规划设计提供依据。

本文研究中母线分为交流母线和直流母线两类，由于能耗计算主要考虑对比交直流母线能耗差值，而新能源的DC/DC变换损耗在同一运行条件下，接至交流或直流母线时差别不大，为简化算法，本文中不予计算，交流、直流母线配置如图1所示。基于图1的交流、直流母线简化拓扑的基本配置进行本文交直流母线能效计算的定义。

图1 交直流母线配置模型Fig.1 AC/DC bus configuration model

对于交流母线，考虑直流负荷损耗PLoss_DC_Load、光伏逆变损耗PLoss_PV及电池逆变、整流损耗PLoss_Sto三部分，其能耗计算为：

PLoss_AC_Bus=PLoss_DC_Load+PLoss_PV+PLoss_Sto

(6)

对于直流母线，考虑交流负荷逆变损耗PLoss_AC_Load及直流母线与外界交换能量损耗PLoss_DC_Trans两部分，其能耗计算为：

PLoss_DC_Bus=PLoss_AC_Load+PLoss_DC_Trans

(7)

式中，PLoss_AC_Bus为交流母线能耗；PLoss_DC_Bus为直流母线能耗。

首先基于建立的能耗计算公式，在瞬时单母线情况下进行研究。为了明确各部分加入与能效的关系，先从纯负荷情况下求解交直流能耗转换点处直流负荷占比R随负荷利用系数γL变化关系。然后增加光伏装机容量占比和光伏出力系数两个变量，限定光伏出力系数γPV为定值0.8，设置负荷利用系数γL处于[0.3,0.4,0.5,0.6,0.7,0.8]之间，求解交直流母线能效平衡点处直流负荷占比R随光伏装机容量占比ξ变化关系。最后增加储能最大充放电功率比率为变量，限定光伏出力系数为0.8,负荷利用系数0.6，求解能效平衡点处直流负荷占比R随储能最大充放电功率比率SStorage和光伏装机容量占比ξ的变化关系，最终期望得到函数如式(8)，考虑如式(9)几个参数及其偏导进行函数曲线分析。

R=F(γL，ξ，SStorage)

(8)

(9)

此后于三种情景下，结合元件特性和典型日曲线，根据数学模型进行时间维度积分，在日周期内进行能效平衡点求解原理如下：

(10)

研究各情况下最大限度降低直流负荷占比代价最小的点，并探讨平衡点处直流负荷占比的趋势。在纯负荷情况下得到一个直流负荷占比为能效平衡点，在负荷-光伏情况下得到直流负荷占比随光伏安装比率变化曲线为能效平衡点曲线，在负荷-光伏-储能情况下得到一系列不同光伏装机容量占比下，直流负荷占比随储能装机容量变化的曲线为能效平衡线。

最后，根据实际项目拓扑，按本文研究的结论分别进行母线配置和能效计算，验证研究结论正确性，并说明该项目母线选择的合理性，同时证明该项目规划拓扑相对传统拓扑具有能效优势。

2.3 瞬时情况下单母线能效分析

2.3.1 纯负载交直流母线能效计算分析

考虑瞬时、纯负载情况下，以负载利用系数为变量、直流负载占比为因变量，求解交直流母线能效平衡点处二者变化关系。该点亦为交、直流母线能效优势转换点，为判断设置何种母线、变量如何配置具有能效优势提供较为明确界线。

交、直流负荷，负荷利用系数、线路长度(用电点)、电压等级相同情况下，求解交、直流母线能效平衡点。考虑到电力设计时需考虑的负荷利用系数和安全系数等因素，直流母线总换流器按日常负荷用电功率时负载率为77%进行配置，代入式(1)得到直流母线取电损耗率ηT，直接接于各负荷的换流器根据负荷安装功率配置，将负荷利用系数代入式(1)，计算得到其损耗率ηL交流负荷损耗如下：

PLoss_AC_Load=PACηL

(11)

PLoss_DC_Trans=(PDC+PAC+PLoss_AC_Load)ηT

(12)

将PLoss_DC_Trans和PLoss_AC_Load代入式(7)求得直流母线损耗。

交流母线损耗率为：

PLoss_AC_Bus=PDCηL

(13)

求解功率平衡点为：

PLoss_AC_Bus=PLoss_DC_Bus

(14)

解得直流负荷占比为：

(15)

(16)

由式(16)解得，当γL=0.918 9时，曲线斜率为0，该点值仅与换流器损耗参数有关，此时平衡点处，直流负荷占比需求达1.028，无法实现。当γL<0.918 9时R为γL的增函数，当γL=0.77与换流器负载率一致时，平衡点处直流负荷占比需求达到1，此后再增大γL，平衡点处直流负荷占比需求大于1，即使全部负荷均为直流，配置直流母线也不能使得其能效优于交流母线。而当γL>0.918 9时，R为γL的减函数，当增大至γL=1时，平衡点处直流负荷占比需求为1.02左右，依旧无法实现。可见在负荷利用系数γL达到换流器设计负载率后，配置直流母线无法获得能效优势。

若以直流负荷占比为纵坐标，负荷利用系数为横坐标，由式(15)做曲线，在γL<0.77时，斜率变化较小，二者近似成正比，此时对位于曲线上方的点，配置直流母线具有能效优势。

2.3.2 考虑光伏的交直流母线能效计算求解

增加光伏接入，同样以直流负荷占比为因变量，求解交直流母线能效转换点。此时，共存在四个自变量：光伏出力系数、光伏安装容量、负荷容量、负荷利用系数。

(17)

式中，γTrans为母线交换能量负载率。

PLoss_DC_Trans=(PLoad+PLoss_AC_Load-PPV)ηT

(18)

PLoss_PV=PPVηPV

(19)

以上结果代入式(7)计算直流母线损耗，代入式(6)计算交流母线损耗，然后求解式(20)：

PLoss_DC_Bus=PLoss_AC_Bus

(20)

解得：

(21)

(22)

式中，ηPV为光伏并网损耗率，由γPV代入式(1)而来。

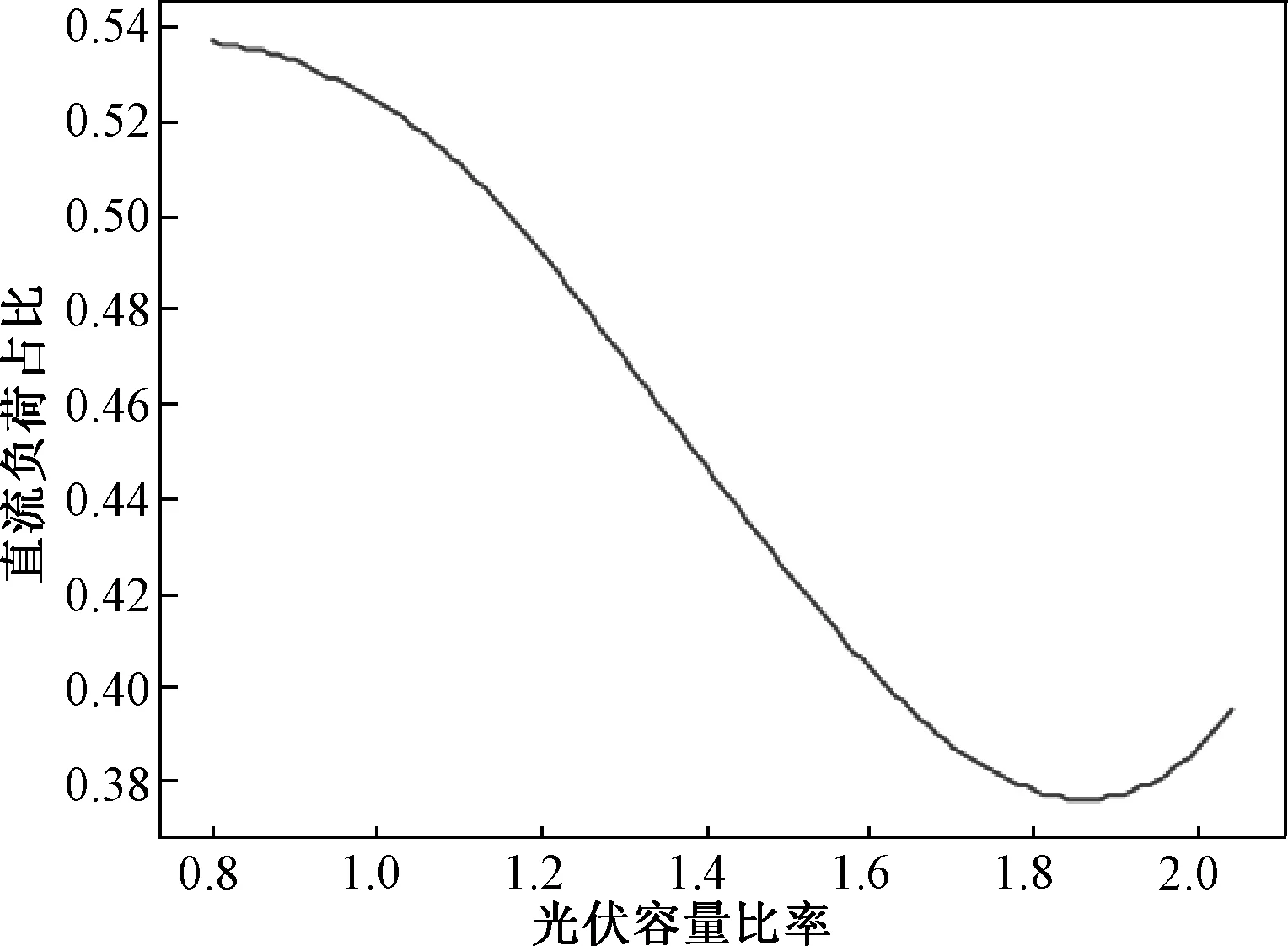
为了在不同光伏装机容量占比下得到使得直流母线占据能效优势的最小的直流负荷占比，在式(21)中，先限定光伏出力系数为0.8(确定ηPV以及γPV)，设置负荷利用系数[0.3,0.4,0.5,0.6,0.7,0.8](确定变化的γL序列)，以光伏装机容量占比为自变量，直流负荷占比为因变量，所得结果如图2所示，同时对R求ξ的偏导如式(22)，图2中，按箭头指示方向，从下至上曲线对应的负荷系数分别为0.3、0.4、0.5、0.6、0.7、0.8。可见，在任意负荷利用系数下，随着光伏装机容量占比增大，直流负荷占比逐渐降低，结合式(22)，当ξ较小时，其对ηT影响不占主导，此时导数小于0，为减函数，此后达到一个极小值点，此时安装光伏对降低能效平衡点处直流负荷占比效益较好；同时随着负荷利用系数逐渐接近光伏出力系数，光伏装机容量占比为1.05左右时，能效平衡点所在曲线的最低直流负荷占比逐渐降低到0。

图2 光伏装机容量占比与平衡点处直流负荷占比关系Fig.2 Relationship between PV installed capacity ratio and DC load ratio at equilibrium point

不同地区的光伏出力系数不同，为了得到不同光伏出力系数对交直流能效平衡点处光伏装机容量的影响，对式(21)，限制负荷利用系数为0.8和1(确定γL)，研究使直流负荷占比R为0的点随光伏出力系数变化情况，做图3，图3中，按箭头指示方向，从下至上曲线对应的负荷系数分别为0.4、0.6、0.8、1.0。随着负荷利用系数增加，曲线向右上方移动，而结合式(21)可知，光伏安装容量比率ξ与出力系数γPV近似成反比例关系。

由上可知，在瞬时功率、光伏配合负荷的情况下，采用光伏装机容量降低直流负荷占比具有效益最优点；随着负荷利用系数增大接近光伏出力系数，效益最优点处直流负荷占比逐渐接近0，而随着光伏出力系数增大，能效平衡点处光伏装机容量比率减小。因此，瞬时直流母线配置中，负荷处有条件配置光伏时，装机容量应接近效益最优点，以保证在能效和效益方面均具有一定优势。

2.3.3 增加储能的交直流母线配置

由于负荷利用系数取决于工程实际情况，光伏出力取决于地区光照实际情况和安装情况。现限定光伏出力系数为0.8,负荷利用系数0.6，不考虑储能容量，只考虑储能最大瞬时功率。由于交、直流母线运行在同负荷、同光伏的情况下，此时储能的充放电功率差值为交直流负荷、光伏、储能的换流器损耗。由于储能装置充放电效率较高(可达99%)[25]，交、直流母线储能充放电损耗的差别较小，对能效平衡点计算结果影响不大，在计算瞬时功率交、直流母线能效平衡点时可忽略。分别计算交、直流母线能耗如下:

PRemanent=PAC+PLoss_AC_Load+PDC-PPV

(23)

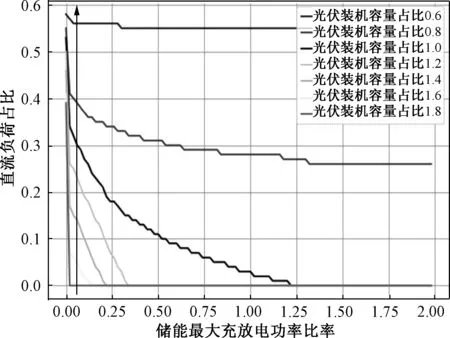
若PRemanent

(24)

将γTrans代入式(1)计算可得ηT：

PLoss_DC_Trans=PReηT

(25)

代入式(7)计算即可得直流母线能耗。

计算交流母线能耗：

PRemanent=PLoad+PLoss_DC_Load+PLoss_PV-PPV

(26)

若PRemanent

(27)

(28)

PLoss_Sto=PStorageηStoλ

(29)

代入式(6)即可得交流母线能耗。

求解：

PLoss_DC_Bus=PLoss_AC_Bus

(30)

式中，PRemanent为母线剩余功率；PRe为母线与外界交换功率；γSto为储能换流器负载率；ηSto为储能装置换流器损耗；PStorage为母线上需要增补的能量；PLoss_Sto为母线上储能装置交直流交换的损耗。

求解交直流母线能耗转换点，所得散点解，使用Matlab安插值法绘制三维图形如图4所示。可见在直流负荷占比为0的平面上有2条交线，为使光伏安装比率和储能最大功率比率均较小时，平衡点处直流负荷占比最小，选取靠近零点处交线效益更优。

图4 光伏比率、储能功率比率和直流负荷占比关系Fig.4 PV ratio, energy storage power ratio and DC load ratio

临界线如图5所示，在该线上，储能最大功率占比和光伏装机容量占比近似呈现线性关系，二者之和约为0.90。

图5 临界处光伏装机容量比率、储能功率比率关系Fig.5 Critical PV ratio, energy storage power ratio relationship

可见，在直流负荷占比为0平衡线上进行直流母线配置，可以在较高效益、直流负荷占比无限制的情况下，保证配置直流母线具有能效优势。

3 基于时序的母线及系统规划配置

考虑日周期，规划设置交、直流母线在各种母线配置情况下对母线、系统能效的影响，按江苏项目数据，选择负荷典型日曲线如图6所示，光伏出力典型日曲线如图7所示。换流器损耗计算同式(1)。

图6 负荷典型日曲线Fig.6 Typical load daily curve

图7 光伏典型日曲线Fig.7 Typical photovoltaic daily curve

以5 min为采样间隔进行能耗计算，基于瞬时计算，采用二分法用计算机分别求解纯负荷配置、增加光伏配置、配合储能三种情况下日周期内的交、直流单母线能效平衡点，如图8所示。

图8 考虑光伏的日周期能效平衡点曲线Fig.8 Diurnal cycle energy efficiency equilibrium curve of photovoltaic is considered

日周期下配置时，按式(10)对式(14)、式(20)、式(30)两端在时间维度上积分。考虑实际采样间隔采用5 min采样求解如下：

(31)

考虑源-荷-储配合情况下时，为了简化问题，假设储能容量充足且储能单独服务于母线源-荷差值调节时，只考虑储能最大充放电功率相对负荷容量比率，在python中基于建立的各个数学模型，限定光伏装机容量为[0.8,1.0,1.2,1.4,1.6,1.8,2.0,2.2]，用pandas库进行典型日负荷、日光伏数据的读取；设置全局变量进行不同配置下交流、直流母线能耗的计算与累加，并对交直流母线日损耗能量做差，然后用二分法迭代进行交直流能耗平衡点求解，其结果如图9所示，图9中，按箭头指示方向，从下至上曲线对应的光伏装机容量占比分别为1.8、1.6、1.4、1.2、1.0、0.8、0.6，可见日周期下，光伏装机容量占比达到1以上时，配置储能才可能将平衡点处直流负荷占比需求降低至0，并且当储能最大充放电容量占比达1.25以上后增加储能充放电功率来降低平衡点处直流负荷占比较为不经济。保持直流负荷占比不变情况下，当光伏装机容量占比达到1.8以上时，增加光伏装机容量占比来减少储能最大充放电功率投入的作用不大。

图9 储能最大功率比率与直流负荷占比关系Fig.9 Relationship between maximum power ratio of stored energy and proportion of DC load

图10为现场两种不同运行方式下的简化拓扑结构图，共计设置直流母线两处，交流母线一处，按配置方案进行验证。DC375 V母线，配置储能不配合新能源发电、直流负荷占比为1；按此前日曲线研究纯负荷母线配置情况下，该母线配置大于能效平衡点0.96，无论储能如何配置，设置直流母线应当具有能效优势。经计算设置的直流母线日损耗约为140.33 kW·h，设置的交流母线日损耗约为156.14 kW·h，符合预期。DC750 V母线，配置直流负荷占比为1，光伏装机容量比率为0.233，储能占比为0.115，经比较可见其配置位于此前综合考虑储能、光伏、负荷情况下的能效平衡点之上，配置直流母线能耗应低于配置交流母线。经计算得直流母线日损耗为1 649.708 kW·h，交流母线日损耗为2 243.28 kW·h，符合预期。

AC400 V母线，交流负荷占比为0，由于地域原因风机发电量基本可忽略、光热按光伏计，由于母线未配置储能，按考虑光伏日曲线的交直流能效平衡点曲线可知，交流母线能效应高于直流。经计算验证,设置直流母线损耗为497.59 kW·h,设置交流母线损耗为101.335 kW·h，符合预期。

对两种运行方式分别计算系统能耗，可得工频变加VSC方案全天候损耗为1 948.79 kW·h，电力电子变压器方案全天候损耗为824.38 kW·h，可见电力电子变压器方案能效较优。

4 结论

本文根据能效针对交直流母线配置问题，进行交直流母线能效平衡点的研究。根据江苏某实际工程，建立光伏、负荷数据模型，换流器、储能损耗模型；在瞬时功率和日周期曲线下，分别在纯负载情况、负荷-光伏情况及光伏-负荷-储能情况下对交直流母线能耗情况进行对比分析，研究交直流母线能效平衡点位置。最后按实际工程各直流母线配置对该方法进行验证，并计算实际工程不同运行方式下的能耗并进行对比，主要得出以下结论：