基于ZMNL的Pareto杂波功率谱仿真改进方法

傅俊滔，陆 宇，刘庆林，何玉洁，桑宏伟，吕 勇

(95859部队，甘肃酒泉 735018)

0 引言

在复杂环境下，雷达回波中的背景杂波直接影响雷达的工作性能[1-2]，对其特性进行研究具有重要意义。随着雷达分辨率的提高，杂波模型已经与早期提出的Rayleigh分布等模型[3]不符，K分布和Pareto分布模型的出现，在理论层次和与实际杂波的拟合程度上都更具有优势[4-5]。

杂波仿真的方法一般有球不变随机过程(spherically invariant random process, SIRP)法和零记忆非线性变换(zero memory nonlinearity, ZMNL)法两种[6-7]。Pareto分布的结构变量可以通过倒数变化得到K分布的结构变量[8]，因此Pareto分布的杂波模拟研究可以借鉴K分布的杂波模拟方法。文献[9]利用SIRP法产生K分布的杂波，优点是其幅度分布能够独立控制，但是计算量较大。文献[10]和文献[11]采用的是ZMNL法，在生成K分布杂波时需要将形状参数进行近似处理或者拆分处理。文献[12]解决了ZMNL法中形状参数取值受限的问题，利用逆Gamma分布和逆Beta分布的乘积来生成任意形状参数值的Pareto分布，但是没有对Pareto分布杂波的功率谱特性进行研究。

海杂波的自相关函数可以表示功率谱特性，一般采用高斯模型进行建模，功率谱呈现出对称的特点[13-14]。由于实际海杂波的功率谱不一定是对称的，该方法无法模拟非对称形状的杂波功率谱，从而使杂波功率谱的仿真受到了限制。文中针对ZMNL法中功率谱模型受限的问题，在文献[12]解决了形状参数取值的基础上，提出了一种产生功率谱为非对称形状的杂波模拟方法，该方法在频谱泄漏水平满足要求的前提下，能够得到非对称形状功率谱的Pareto分布杂波。

1 杂波模型及模拟方法

1.1 Pareto分布杂波模型

服从Pareto分布的海杂波X是复合高斯模型，其概率密度函数(probability density function，PDF)可视为结构分量与散斑分量作用的结果，其表达式为[15]：

(1)

其中，pY(y)是结构分量的PDF。可表示为：

(2)

式中：Γ(·)为Gamma函数；a为形状参数，其值决定PDF的形状；b为尺度参数，其值决定支撑域的起点。

pX|Y(x|y)是散斑分量的PDF，可表示为：

(3)

1.2 ZMNL方法

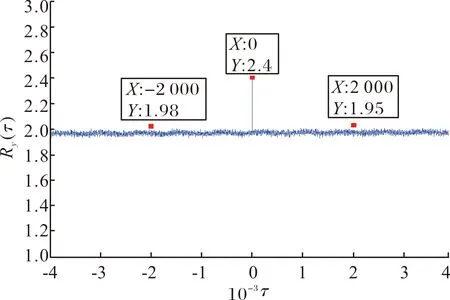
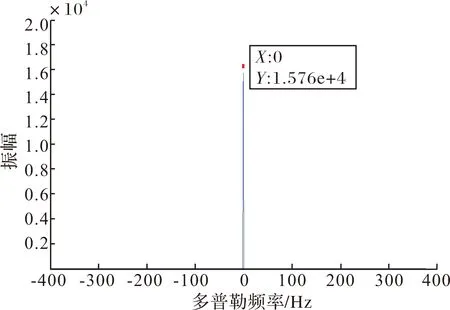
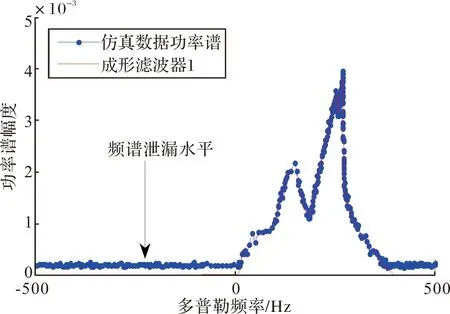
假设两个独立随机变量z～IG(z;p+q,1)，τ～IBe(τ;p-r,q+r)，那么随机变量γ=zτ～IG(γ;p-r,1)[12]。其中，p和q为整数，0

(4)

(5)

文献[12]中没有对杂波模拟的功率谱特性进行分析，如果依然采用传统的方法对海杂波的功率谱进行仿真，不仅计算复杂，而且只能得到对称的功率谱模型。对于实际采集得到的海杂波来说，其功率谱不一定是对称的，因此，杂波功率谱的模拟存在限制，需要进一步研究。改进的Pareto杂波模拟框图如图1所示。

图1 改进的Pareto分布杂波模拟框图

2 改进的Pareto杂波模拟方法

为了简化表达式，设图1中的p+q为v，2a2为ε，那么图1中y服从平方根逆Gamma分布，其PDF为：

(6)

假设yi和yj相互独立，那么y的自相关函数R(yi,yj)为：

(7)

E[y]表达式为：

(8)

令t=ε/y2，代入式(8)可得：

(9)

E[g]表达式为：

(10)

令t=ε/g，代入式(10)可得：

(11)

Ry(τ)为：

(12)

由维纳钦欣定理可得，y={y1,y2,…,yN}的功率谱Sy(w)是对Ry(τ)进行傅里叶变换：

(13)

对式(13)进行分析，可得：

(14)

Sy(w)的值可以近似表示为：

(15)

此时，图1中的输出γ={γ1,γ2,…,γN}的功率谱Sγ(w)为：

(16)

其中，Sz(w)为图1中复高斯序列z={z1,z2,…,zN}的功率谱。令K为一个足够大的系数，那么，可以将式(14)改写为式(17)：

(17)

当N和K为定值时，式(14)成立的条件是v值需要达到临界值，并且当v值足够大后，v值的增加对式(14)的影响很微弱。当v值没有达到临界值时，Sγ(w)便不满足式(16)，式(13)中的第二项便不能忽略不计，功率谱将出现频谱泄漏的现象。此时，图1中Sγ(w)为：

Sγ(w)=ASz(w)+B

(18)

式中，A和B分别为：

(19)

(20)

图2 y序列的自相关估计

当v=2.25，ε=3，理论值由式(12)可得：

(21)

对比图2中的3个点，可以发现估计值与理论值的大小几乎相等。因此，可以证明式(10)和式(11)理论推导的正确性。

图3 仿真数据的功率谱

Sy(0)=(8000-1)×1.97+2.4=15760.43

(22)

通过以上计算可知，假设v值大小恰当，y的功率谱是冲击响应函数，那么复高斯序列z的功率谱形状决定了模拟杂波功率谱Sγ(w)的形状，而复高斯序列z的功率谱形状是由图1中的成形滤波器|H(w)|的形状决定的。因此，只要成形滤波器|H(w)|的形状不是对称的，那么模拟杂波功率谱Sγ(w)的形状就可以是不对称的。而在设计时，对滤波器|H(w)|的形状是没有硬性要求的，所以滤波器|H(w)|在理论上能够为任意的形状。

3 仿真性能分析

为了检验输出的功率谱是否具有非对称性，在MATLAB中进行仿真和验证。首先给出仿真数据的参数，如表1所示。

表1 仿真参数表

表1中的形状参数取值为非整数，这是为了区别于传统的ZMNL法的形状参数不能为非整数的情况。用MATLAB设计一个功率谱具有非对称形状的成形滤波器，这也是最终输出功率谱期望得到的形状，其曲线如图4所示。

图4 成形滤波器

根据周期图法，可以生成模拟的输出功率谱图像。图5为形状参数v1=3.75时，通过成形滤波器的功率谱形状。

由图5可知，模拟的输出功率谱与其相应的成形滤波器在形状上非常相似，即满足功率谱不对称的特点。此外，仿真的功率谱形状存在一定程度的频谱泄漏，这是由于式(18)中存在的B项引起的，与理论推导的结论一样。

图5 模拟功率谱与成形滤波器1对比

图6为形状参数v1=1.05时，通过成形滤波器的功率谱形状。

图6 模拟功率谱与成形滤波器2对比

观察可知，图6仿真的输出功率谱存在一定的频谱泄漏，与其对应的成形滤波器的形状相似，具有不对称的特点，与图5中得出的结论一致。

观察形状参数取不同值时通过同一成形滤波器的图像，即图5和图6。对比发现，形状参数v1=3.75对应图像的频谱泄漏程度要低于形状参数v1=1.05对应图像的频谱泄漏程度。这是因为当形状参数取大值时，式(18)中的B项对输出功率谱的影响很小。而随着形状参数值的减小，B项对输出功率谱的影响越来越大，造成的频谱泄漏程度也越来越高，这与前面的理论推导一致。因此，在Pareto杂波模拟的仿真中，形状参数的取值要合适，而且不能太小，这样生成的杂波才能既满足幅度分布，又满足功率谱非对称性的要求。

4 结束语

研究了ZMNL方法中Pareto杂波的功率谱仿真问题。得出如下结论：只要形状参数选择恰当值，其频谱泄漏水平在要求的范围内，那么就能够生成形状参数为非整数、功率谱为非对称形状的Pareto分布杂波。