简化变换模型的航拍图像拼接技术
2021-10-27李艳玲汪国平
李艳玲, 汪国平
(1 长治学院计算机系,山西长治 046011;2 北京大学信息科学技术学院,北京 100871)
0 引言
无人机航拍拼接技术通过对一系列重叠航拍影像的拼接,实现对原物的准确重建。该技术已广泛应用于虚拟现实技术、应急响应、气象及地震监测、计算机视觉等领域。由于无人机航拍影像涉及多个视点和场景,相邻图像之间旋转角变化大,相机位置不断变化,场景深度又很难获知,使得影像匹配和拼接困难,对后续全自动处理造成影响。
拼接技术是通过全局变换对齐待拼接图像,将各图像变换到统一平面。常见的全局变换包括相似变换、仿射变换、投影变换和非线性变换。文献[1]利用投影变换进行全局配准,自动从视频序列构建全景图像。文献[2]采用局部不变特征匹配图像,采用球面投影在无序数据集中识别多个全景图。文献[3]提出适应场景内容的投影变换算法,使广角失真最小化,但对齐能力不够,无法很好地产生多视点图像。文献[4]将场景划分为背景平面和前景平面,利用两个单应性矩阵分别对齐两个平面,从而实现全景场景的无缝拼接。文献[5]提出移动DLT(direct linear transform)算法,将图像划分为密集网格,每个网格都用一个单应性矩阵对齐,从而显著减少重影。文献[6]提出深度网络结构,基于SIFT生成训练样本。文献[7-9]分别探讨了深度学习在图像拼接中的应用,并与经典方法进行了比较。文中算法简化变换模型,扩大可拼接范围同时避免产生明显透视畸变,并局部融合图像以获得更好的视觉效果。
1 算法流程
整个算法流程主要包含特征点匹配、确定拼接顺序、图像变换和图像合成模块,继而生成最终的拼接结果。
步骤1 提取图像的特征点。根据SIFT特征的局部极值性,对于图像In,不需要重新提取特征,只要增量式的将新拼接部分的特征加入图像序列{I1,I2,…,In}中即可。
步骤2 确定变换模型。估计运动参数,求解相似变换,获得拼接结果。
步骤3 匹配特征。为了保证特征匹配的正确性,采取双向匹配策略消除错误匹配。
步骤4 图像合成。
2 图像变换
由于投影变换可以较好地对齐图像,而在图像的非重叠区域,用相似变换替代投影变换。相似变换相当于平移变换、旋转变换和均匀缩放的复合,因此相似变换不会产生形状失真。图像可以通过均匀缩放及叠加必要的平移和旋转来重合另一图像。
拼接过程中每幅图像尽可能进行相似变换,使得视线不发生改变,从而简化变换过程,同时保证较好的精度。
2.1 运动参数估计
图像拼接的研究基于摄像机每次拍摄焦距没有变化的假设,拼接过程中仍需要对图像变换对齐,其中运动参数估计是最困难的一步。
对于场景中任一三维点(x,y,z)和其在图像中的投影坐标(u,v)的关系为:
(1)
式中:s为缩放因子;f为摄像机的焦距;(cx,cy)为图像中心坐标的偏移;R和t分别表示摄像机的旋转和平移。摄像机坐标系向图像坐标系变换时会引入畸变,导致原始图像失真。如果已知摄像机的相对位置R和t,图像间可以直接精确映射的情况只有3种:1)摄像机平移参数t=0;2)有场景深度图,即向量已知;3)近似平面场景。
航拍图像拼接一般是针对多视点的拼接,摄像机平移不可忽略,场景深度又很难获知,因此情况1)和情况2)均不成立。通过分析航拍图像性质,不难发现当拍摄高度与场景最高点的距离超过100 m时,可将一定范围的大地近似为平面区域,因此“平面场景”的假设基本成立。在这一假设下,图像间的映射退化成了单应性矩阵。单应性矩阵将两幅图像之间做了完全等价的映射,相当于对图像做了变视点操作,可将所有图像变换到同一现有视点下。但是单应性变换会产生严重的透视畸变。而且该视点在高度和平面投影的限制下,最终的拼接视角会严重受限。假设图像拍摄角度是垂直向下的,图像间的映射近似于相似变换。而且拍摄高度越高,近似精度越高。且航拍图像序列中相邻两帧图像间视差较小,因此用相似变换代替单应性变换,既能保持视线方向不发生改变从而保留原图像视点,又能平衡拼接精度[10]。相似变换没有变视点特性,同单应性矩阵相比,在保留原图像视点和拼接精度之间做了平衡,如图1所示,图1(a)右侧出现明显的透视畸变,同时可拼接范围大大减少。

图1 单应性变换和相似变换拼接比对
2.2 图像匹配
根据SIFT特征局部极值性,对于已拼接好的结果,只需增量式拼接到累积结果上。为了确保特征匹配完全正确,改进特征验证算法,采取双向认证策略:
(A→B)∩(B→A)
(2)
式中:A→B为图像A的特征在图像B的特征集中做查询;B→A则为图像B的特征在图像A的特征集中做查询。若图像A有一个特征点和图像B相匹配,那么再检测图像B是否也在相应特征点上与图像A匹配,如果匹配成功,则认为该匹配是正确的,否则是错误匹配。如果只做单向验证,一个特征点可能对应多个匹配,显然是不正确的,而双向验证可以消除错误匹配,提高匹配精度,不至于出现大范围的错误累积从而影响拼接质量[11]。
2.3 图像变换投影
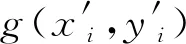
(3)
式中s和t是由f到g的坐标变换函数,可以通过找到产生畸变的转换函数完成图像校正。但实际中很难对复杂的几何失真过程建模,而投影变换可以很好地描述几何失真模型,投影变换函数H:P2→P′2定义为在齐次坐标系上的线性变换。利用DLT算法,计算变换矩阵。
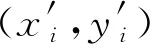
(4)
式中h1~h8为投影变换的8个参数。
(5)
式中θ为点(xi,yi)的旋转角度。
根据相似变换,有:
(6)
式中a,b,c,d为旋转平移参数。
由于前两行线性独立,所以得到:
(7)
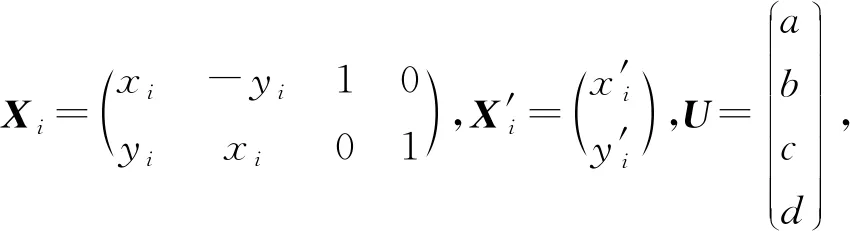
对齐次线性最小二乘问题优化,得到最终的相似变换矩阵argmin‖XU-X′‖2。图像变换投影如图2所示。

图2 图像变换投影
3 图像合成
3.1 图像曝光度
求解待拼接图像重叠部分的最佳接缝,将图像拼接在一起。对少数光照差异较大的图像直接拼在一起,会影响下一次的特征提取和拼接。因此接缝之前做一次曝光补偿,减少图像间的亮度差异。
灰度直方图是图像亮度明暗程度的表现,包含丰富的曝光信息[12]。曝光不足和曝光过度表现为侧边缘有大量像素点堆积。如图3所示,图(a)曝光过度,直方图波形主要体现在右侧,亮部数值过多。图(c)曝光不足,直方图则体现在左侧,显然暗部数值太多。图(b)是曝光适度的情况,其直方图既有亮部数值,又有暗部数值。
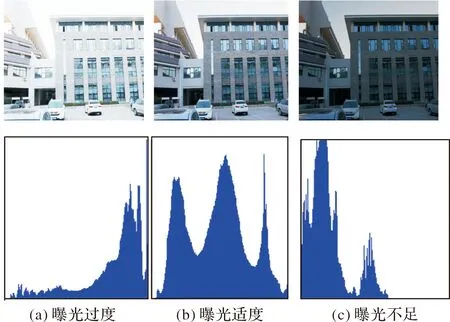
图3 不同曝光图像及灰度直方图
由于天气、光线因素影响或物体表面反光,航拍图像存在少数差异较大情况。在图像曝光不足时,画面虽然比较暗,灰度值集中在0至20。在曝光过度时,图像在255色阶附近的像素呈一条直线。因此统计偏暗的像素个数或偏亮的像素个数,评估图像是否曝光过度或曝光不足。令nk表示灰度为rk的像素个数,则曝光度可表示为:
(8)
即
(9)
式中:M,N表示图像的行和列;L0代表曝光不足时像素数,此时δ1和δ2分别取0到20;L255代表曝光过度时像素数,δ1和δ2取250到255。曝光情况判断条件如表1所示。

表1 曝光判断条件
表中α,β为预设参数,通过对大量航拍图像实验分析,α取2%,β取10%可以得到比较理想的结果。
对图像重复如下步骤:
步骤1 判断图像曝光情况。
步骤2 图像预分块,每个块计算增益因子。
步骤3对每个图像的增益因子矩阵做平滑滤波,更好适应图像部分区域曝光差异的情况。
由于增量式拼接数据量较大,为了提高曝光补偿速度,对于待拼接图像,只选择与拼接图像有交集的块,计算出增益因子后再做平滑滤波。最后拼接图像除以待拼接图像对应块的增益因子[13]。
图4是航拍图像一次曝光补偿的局部效果图,图4(b)可获得较好的视觉效果。
3.2 图像融合
将M×N的图像I(M,N)映射为无向图G=
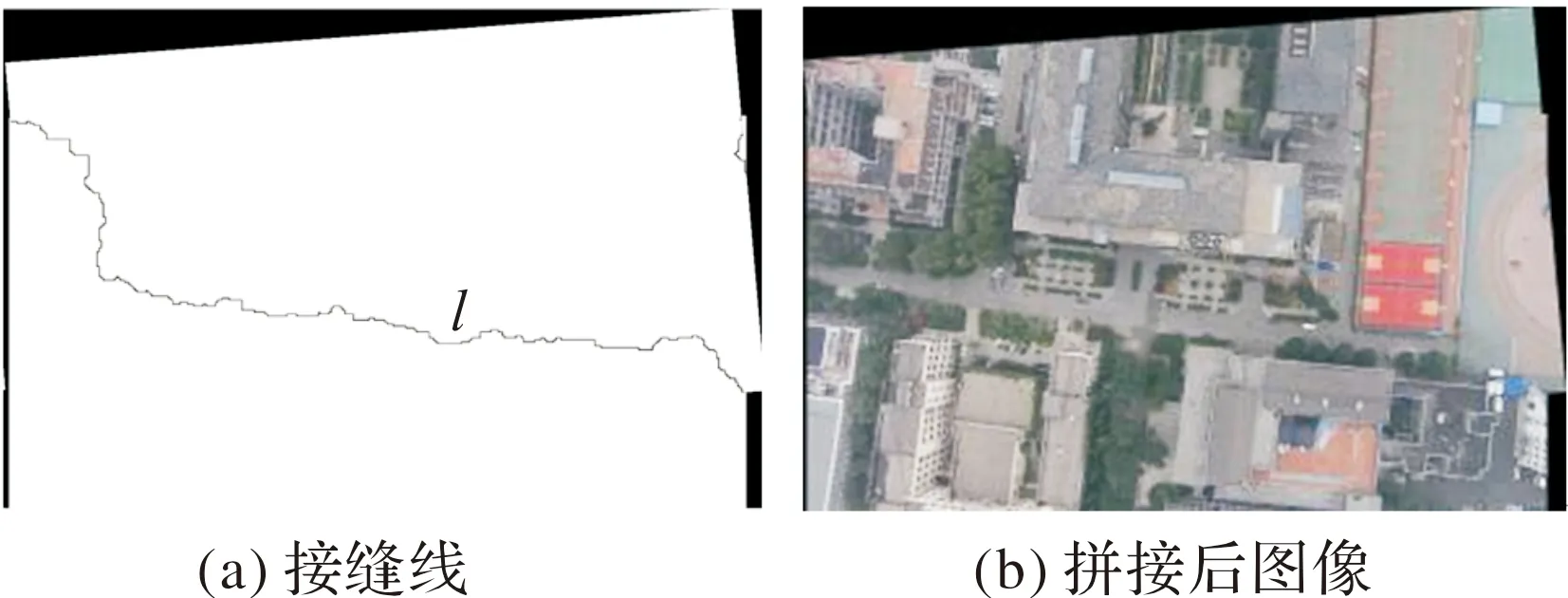
图5 图像接缝线
接缝之后沿接缝线加权融合图像。由于航拍图像分辨率大,做全局的融合对时间和空间的开销都非常大,因此,可以采取距离图加权的方法局部图像融合。结合直方图匹配消除相邻图像接缝两侧的灰度差异,若一次性匹配效果不好,可多次调整,直到取得比较满意的视觉效果。
选取某校30张航拍图像,用基于全局的算法和文中两种算法进行拼接实验,其成功匹配点对数和总运行时间如表2所示。

表2 算法比较
从表2可以看出,文中算法可大大提升匹配的点对数目,由于不必每次重新提取特征,运行时间也有所缩短。
4 结束语
在“平面场景”假设下,文中算法用相似变换近似图像间映射,简化变换模型,图像不会产生形状失真并保持视点不发生改变。使用Graph-Cut算法计算重叠部分边界,沿边界完成图像融合,继而生成最终的结果。
