固体推进剂药柱点火瞬态裂纹尖端场研究

2021-10-27高双胜

弹箭与制导学报 2021年4期

龙兵，高双胜，金伟

(1 常州工学院航空与机械工程学院，江苏常州 213032；2 96811部队，浙江江山 324109)

0 引言

固体火箭发动机是导弹武器系统的动力装置，其结构完整性是动力系统乃至整个武器系统安全性和可靠性的重要影响因素。发动机装药在生产、运输和使用过程中，会受到温度、机械振动和冲击等载荷作用。研究表明[1]，装药产生裂纹和脱粘等缺陷的主要原因是过载冲击和温度变化所产生的伸缩变形。裂纹会破坏固体发动机的结构完整性，严重时甚至可能引起爆燃爆轰，造成灾难性事故[2]。因此开展点火瞬态发动机装药的动态断裂研究十分必要。

近年来，国内外学者针对固体推进剂的动态断裂性能开展了一定的试验研究。Ho等[3]使用霍普金森杆和动态热分析(DMA)研究了复合固体推进剂断裂特性与其动态粘弹特性的关系。龙兵等[4-5]开展了固体推进剂的低温断裂性能的试验研究，结果表明温度和应变率对推进剂的断裂性能具有重要影响。汪文强等[6]利用SHPB技术，对CMDB推进剂进行了冲击断裂试验，研究结果表明CMDB推进剂动态断裂韧性表现出明显的线性率敏感特性，其在高过载条件下表现出明显的脆性起裂特性。赵汝岩等[7]进行了含典型裂纹装药结构点火瞬态的压强变化试验研究，结果表明较深裂纹尖端的压强远高于燃烧室压强，易引发爆炸事故。

随着数值计算技术的发展，越来越多的学者开始使用有限元法分析发动机装药的断裂问题。Han等[8]在考虑应变率相关性的影响基础上，建立了一种应变率相关内聚力本构，仿真结果和试验所得结果基本一致。李东[9]通过建立由三维非线性粘弹性本构关系描述的固体推进剂有限元模型，研究了裂纹尖端应力应变场的分布及其对加载速率的响应。但是目前国内外对于发动机装药动态冲击载荷下的数值模拟见诸报道的不多。动态条件下裂纹尖端场的研究不仅可以为裂纹起裂和扩展准则的建立提供理论依据，并且可以检验数值解的正确性。

为研究发动机药柱在点火瞬态时的动态裂纹尖端场，建立管形含裂纹药柱结构的有限元模型，计算得到固体推进剂药柱动态裂纹尖端的应力应变场，分析其变化规律；在此基础上得到裂尖区域的张开应力分布，并计算动态应力强度因子。

1 固体推进剂不可压缩Ⅰ型裂纹尖端场

在裂纹尖端附近，也就是当r趋近于0时，裂尖附近的应力趋向于无穷大，这就是应力奇异性，图1为裂纹尖端应力奇异性示意图。

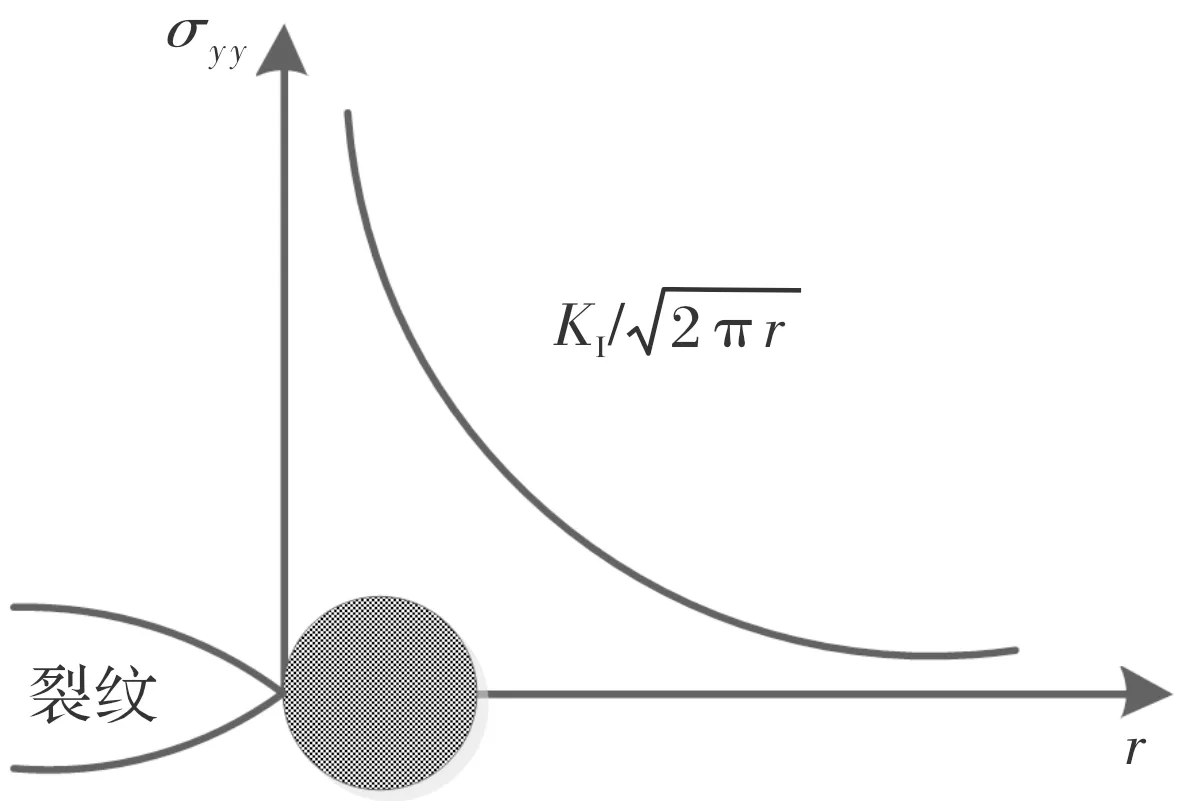
图1 裂纹尖端应力奇异性

对于Ⅰ型裂纹，裂尖应力场可以通过下列方程表示：

(1)

(2)

(3)

式中：r,θ为裂纹尖端附近点的极坐标；KI为应力强度因子，由式(4)计算：

(4)

裂纹尖端位移场可由下列方程描述：

(5)

(6)

式中：ν为材料的泊松比；G为剪切模量。

从以上裂纹尖端应力应变场可以看出，它们都由参数KI，r，θ控制，其中r和θ为坐标参量。因此可以认为在同一结构中，KI为裂纹尖端场的最终控制参量。对于动态裂纹尖端场问题，只需要计算动态应力强度因子，就可以得出动态裂纹尖端场的控制方程：

(7)

(8)

(9)

(10)

(11)

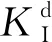
(12)

2 含裂纹固体火箭发动机模型

2.1 有限元模型及网格划分

固体火箭发动机由安全发火机构、点火机构、装药燃烧室和喷管等部分组成。装药燃烧室由高强度合金钢壳体、绝热层、衬层和药柱等组成。装药结构由于受到各种载荷的作用产生裂纹等缺陷，造成结构完整性的破坏。为便于研究，在这里选取装药结构简单，力学特征明显，易于数值仿真建模的内燃式管形装药，药柱结构预制裂纹，分析药柱受冲击载荷作用下的表面裂纹尖端应力应变场。如图2所示带预制裂纹的管型发动机结构示意图，取装药外径R=160 mm，内径r=50 mm，W代表发动机推进剂肉厚，a代表预制裂纹的长度，在这里设置裂纹长度a/W=0.4进行仿真计算。

图2 固体火箭发动机示意图

图3 裂纹尖端的网格细化

2.2 材料参数及边界条件

在点火瞬态载荷的冲击条件下，发动机装药应变和应力表现出明显的线性特征[10-11]，固体推进剂使用线粘弹性本构模型，泊松比为0.496，密度为1.78 g/cm3，常温下固体推进剂松弛模量的Prony级数为:

E(t)=1.172+3.90e-0.5t-3.078e-0.25t+1.709e-0.125t-

0.422e-0.05t+0.633e-0.025t+0.005e-0.0125t

如图4所示假设某发动机的点火升压过程近似为线性，有限元计算时施加如图所示点火增压载荷，Pm为内压。

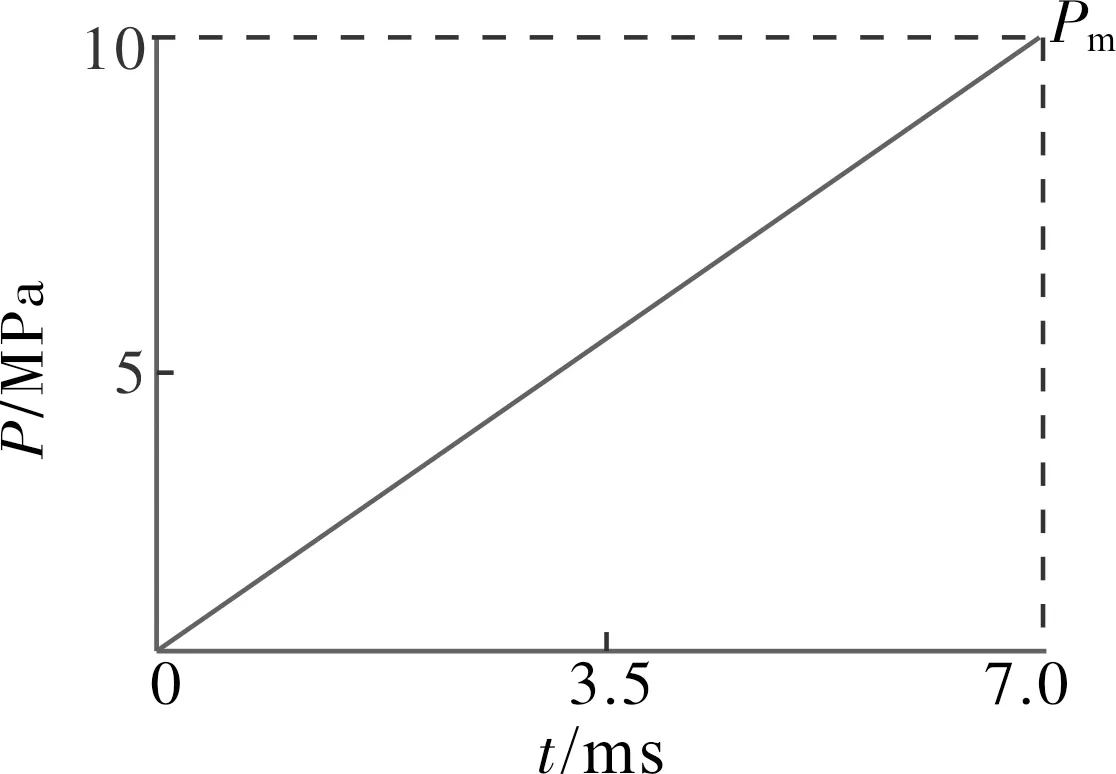
图4 点火增压曲线

3 仿真计算结果与分析

3.1 有限元计算结果

本节主要专注裂纹尖端附近的应力应变场，因此只截取裂纹尖端附近区域计算结果进行研究。图5和图6分别是加载3.5 ms和7 ms固体推进剂裂纹尖端的应力应变场。从图中可以看出，不同加载条件下固体推进剂的裂纹尖端都出现了应力集中现象，推进剂的裂纹前端主要受拉应力的作用；3.5 ms加载和7 ms加载时裂纹尖端的应力应变云图形状相似，裂纹尖端附近的近场应力要比远场应力大1到3个数量级，并且环向应力比径向应力要大；环向应力云图与最大主应力云图的形状较为相似，而径向应力云图的形状则与之差别较大。比较3.5 ms加载云图和7 ms加载云图可以发现，随着时间的增加，裂纹尖端应力应变场的数值逐渐增大。

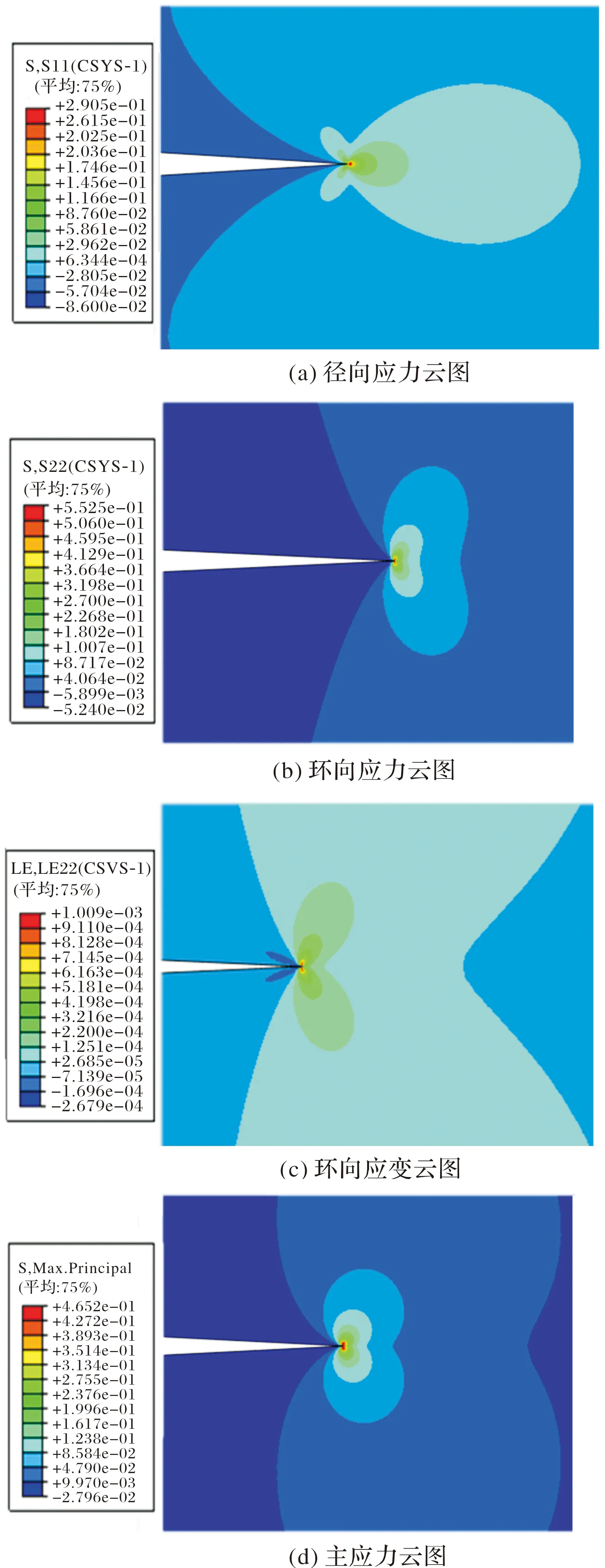
图5 t=3.5 ms时裂纹尖端应力应变场

图6 t=7 ms时裂纹尖端应力应变场

图7和图8是t为3.5 ms和7 ms时裂纹尖端区域的最大主应力与环向应变随距裂尖距离r及角度θ的变化曲线。从图中可以看出，不同条件下最大主应力和环向应变的变化趋势基本相同。随着θ的变化，裂纹尖端附近的应力应变逐渐变化，在θ处于0°～90°时，最大主应力和环向应变随θ的增大逐渐增大；而当θ处于90°～180°时则随着角度的增加而逐渐减小，并且环向应变在120°之后逐渐趋于负值。比较t为3.5 ms和7 ms时的曲线可以看出，随着时间的增加主应力和环向应变逐渐增加。从图中还可以看出，最大主应力和环向应变随着距离裂纹尖端距离r的增加逐渐趋于稳定，在r较小时应力应变的变化梯度明显较大。

图7 t=3.5 ms时最大主应力与环向应变随r和θ变化曲线

图8 t=7 ms时最大主应力与环向应变随r和θ变化曲线

3.2 动态裂纹起始条件

高应变率条件下裂纹的常用动态起始判据有：动态应力强度因子判据、动态J积分判据、最小作用量判据和极小作用时间判据等。固体推进剂在动态条件下一般属于脆性断裂[4]，因此这里使用动态应力强度因子判据：

(13)

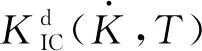
假设Williams[12]级数解的首三项能够表征裂纹尖端应力场，在I型加载条件下θ=0°裂纹面的张开应力为：

(14)

将有限元计算结果与式(14)进行比较，即可验证使用参数KI和A3确定裂纹尖端场是否正确。将式(14)重新排列[13]，可得：

(15)

通过裂尖距离r和裂纹尖端张开应力变化曲线，结合式(15)对曲线进行线性拟合，即可得到KI和A3，然后由式(14)即可得出裂尖附近应力场。图9是t为3.5 ms和7 ms时裂纹尖端附近张开型应力分布有限元计算结果同Williams三项解计算结果对比图。从图中可以看出有限元计算结果和理论预测结果基本吻合，这说明使用上述三项解能够有效描述固体推进剂动态裂尖场。

图9 裂纹尖端张开应力分布有限元计算结果与理论计算结果曲线

通过计算得到KI(3.5)=0.357 MPa/m，KI(7)=0.697 MPa/m。随着时间的推移，固体推进剂的动态应力强度因子增大。同文献[4]的试验结果相比较，可以看出在文中加载条件下固体发动机药柱表面裂纹的动态应力强度因子已经达到推进剂的动态断裂韧性试验值，因此可以认为在这种条件下发动机药柱存在裂纹扩展危险性。