一种适用于空间对称线阵的泄漏目标检测方法

闫林杰，王天琪，郝程鹏，侯朝焕

(1 中国科学院声学研究所，北京 100190；2 中国科学院大学，北京 100049)

0 引言

主动雷达目标检测技术基于信号检测与估计理论测量发射信号的回波数据以检测目标的有无。近年来，以杂波抑制与目标检测为目的的空时自适应检测(STAD)技术得到发展[1-2]。但传统STAD方法大都基于均匀杂波环境[3-5]，实际应用很困难。为此一系列部分均匀杂波环境[6-7]下的STAD方法得到发展。为提高低辅助数据数量时的检测性能，文献[8]设计了部分均匀环境下的斜对称ACE(P-ACE)方法，通过利用空间对称线阵中干扰协方差矩阵的斜对称结构[9]，有效降低辅助数据需求量及运算复杂度。此外，为弥补系统采样时的目标能量泄漏损失[10-11]，文献[12]提出部分均匀环境下的修正ACE(M-ACE)方法。除目标检测外，该方法具有良好的目标距离估计能力。文献[13]在M-ACE的基础上联合使用斜对称特性，设计了斜对称修正AMF(PM-AMF-PHE)方法，进一步提高目标检测性能。

然而，PM-AMF-PHE方法单独使用待检测数据或辅助数据对未知参数进行估计，有限的估计精度制约了该方法的检测性能。基于文献[13]，文中提出了适用于部分均匀环境的改进PM-AMF-PHE(MPM-AMF-PHE)方法，并通过与同类型方法进行仿真对比，证明所提出方法在辅助数据数量受限时具有更好的检测性能。

1 问题描述

1.1 接收信号建模

假设回波由Na个阵元组成的均匀线列阵接收，每个阵元发射的时域脉冲数为Np=1。第l个距离单元接收的离散回波数据可描述为:

zl=sl+nl∈CN×1

(1)

式中:C为复数域，N=NaNp，sl和nl分别为目标信号矢量和包含白噪声、杂波的干扰信号矢量。图1给出脉宽为Tp的矩形脉冲信号的匹配滤波输出。图中显示，当存在目标能量泄漏时，信号的采样点分别位于-ε和Tp-ε处，由此得到由相邻3个距离单元组成的目标能量泄漏采样模型:

图1 矩形脉冲信号的泄漏采样过程

(2)

1.2 二元假设检验

根据定义，上述目标检测问题可以表述为以下二元假设检验：

(3)

式中:H0和H1分别为无目标和有目标的假设；zl为待检测数据矢量；zk为辅助数据矢量。nl和zk统计独立,均为零均值的多元复高斯随机过程，且二者的协方差矩阵仅相差未知的比例因子γ>0。

在使用空间对称线阵的雷达系统中，干扰协方差矩阵M和空域导向矢量υ都具有斜对称特性，则有M=JM*J且υ=Jυ*，J∈RN×N为副对角线为1、其他元素都为0的置换矩阵，R表示实数域。

2 检测方法设计

为求解式(3)中的假设检验问题，基于修正的两步GLRT检验准则设计自适应解决方案。推导过程分为两步：首先假设γ已知，联合待检测数据和辅助数据估计未知参数M和α=[α,α*]；然后基于待检测数据得到γ的MLE，使用估计值替代 ，最终得到完全自适应检测方法。根据第一步，似然比检测表达式为:

(4)

式中:η为一定虚警概率(Pfa)下的检测阈值:fj为Hj,(j=0,1)假设下数据矩阵Z=[ZL,ZK]∈CN×(K+3)的概率密度函数；ZL=[zl0-1,zl0,zl0+1]∈CN×3为待检测数据矩阵；ZK=[zl0+2,zl0+3,…,zl0+K+1]∈CN×K为辅助数据矩阵。

表达式为：

(5)

(6)

式中：t1=-Tp-ε;t2=-ε;t3=Tp-ε。

使用MLE方法估计Hj,j=0,1假设下的M，

(7)

(8)

将式(8)代入式(4)，重新整理为：

(9)

基于式(9)，对α的MLE等价为:

(10)

求式(10)关于α的导数并置零，可以得到估计结果为:

(11)

根据第二步，基于待检测数据求γj的MLE，

(12)

(13)

(14)

将式(11)、式(13)的估计值代入式(9)，得到最终的MPM-AMF-PHE检测法则：

(15)

3 性能分析

在部分均匀背景下，采用蒙特卡洛法分析MPM-AMF-PHE方法的检测概率Pd和距离估计性能。采用等间距均匀线列阵，仿真参数设置为：N=9,γ=3,Tp=0.5 μs,nt=103,Pfa=10-4,f=0,杂波噪声比为10 dB,格搜索精度为Δ=Tp/10,目标波达方向为0°。为使算法性能对比明显，假设辅助数据数量受限(令K=N)和辅助数据数量充足(令K=2N)两种仿真背景，每种背景下均加入PM-AMF-PHE,M-ACE和P-ACE方法作为对比。

3.1 辅助数据数量受限情况

图2为K=N时4种检测方法的Pd随信号杂波噪声比(RSCN)的变化曲线。曲线显示，随着RSCN的增大，MPM-AMF-PHE具有最高的Pd。在Pd为0.9时，MPM- AMF-PHE相较于PM-AMF-PHE,P-ACE和M-ACE分别具有约0.7 dB,3.5 dB和15 dB的性能增益。这表明在辅助数据数量受限的情况下，MPM- AMF-PHE的目标检测性能更优良。

图2 K=N时4种检测方法的Pd随RSCN的变化曲线

图3 K=N时3种检测方法的δrms随RSCN的变化曲线

3.2 辅助数据数量充足情况

图4为K=2N时4种检测方法的Pd随RSCN的变化曲线。

图4 K=2N时4种检测方法的Pd随RSCN的变化曲线

对比图2可以看出，当辅助数据数量增大时，4种检测方法的目标检测性能均得到提升，MPM-AMF-PHE的检测性能优势相较于辅助数据数量受限时有所减弱。在Pd为0.9时，MPM-AMF-PHE相较于PM-AMF-PHE,M-ACE和P-ACE的性能增益分别约为0.3 dB,2.5 dB和3 dB，其检测性能略优于PM-AMF-PHE，但与M-ACE和P-ACE相比，仍具备明显的性能优势。

图5为MPM-AMF-PHE,PM-AMF-PHE和M-ACE的δrms随RSCN的变化曲线。与图3相比，3种检测方法δrms值的变化趋势并未发生明显改变，但距离估计精度均略有提升。

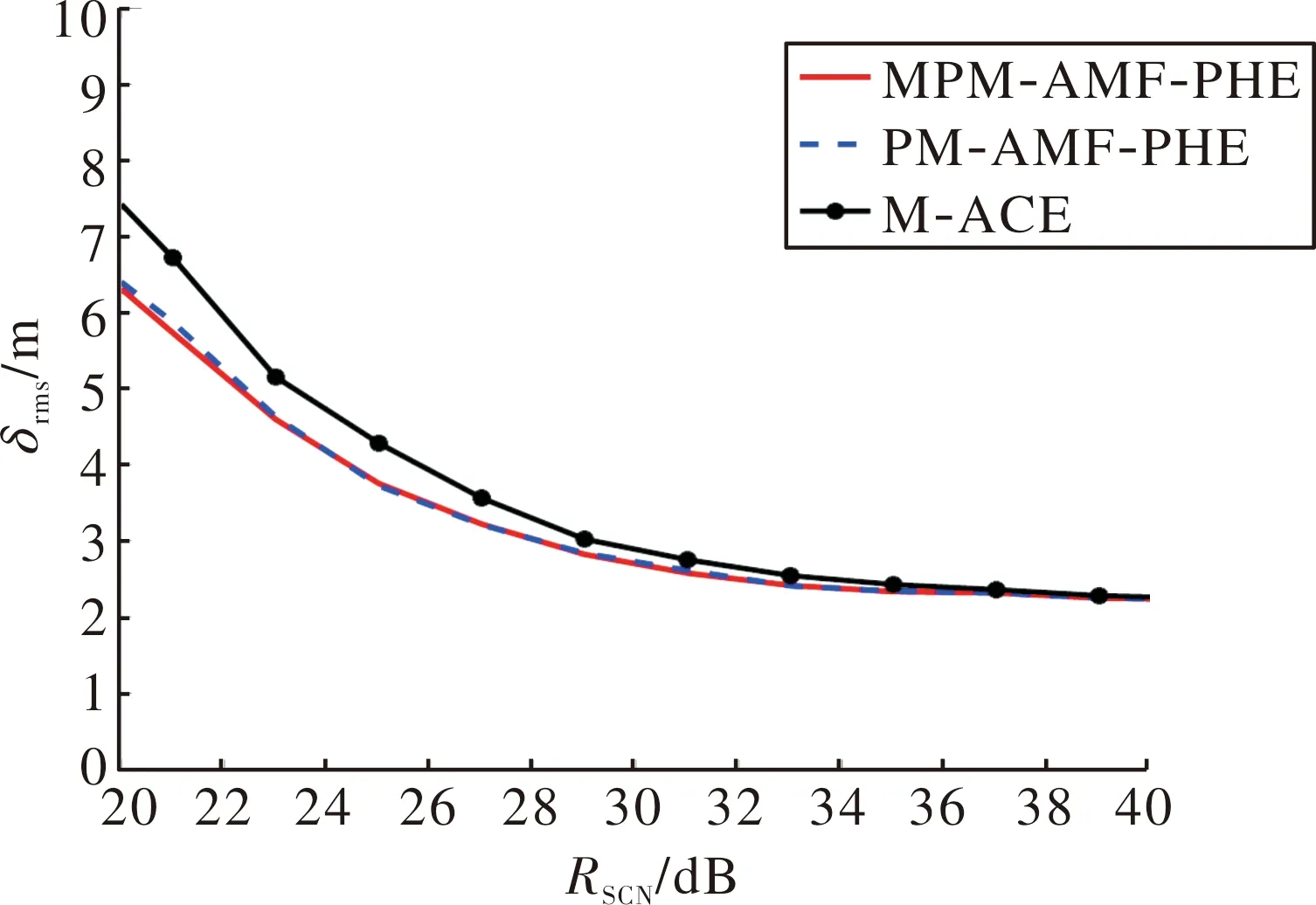
图5 K=2N时3种检测方法的δrms随RSCN的变化曲线

综上所述，相较于同类型检测方法，MPM-AMF-PHE具有更加优良的目标检测与距离估计性能，特别是当辅助数据数量受限时，其性能优势更为明显。因此所提出的方法在目标检测中可以保证较好的稳健性，更具应用潜力。

4 结论

在部分均匀高斯杂波背景下，提出了一种适用于空间对称线阵的泄漏目标检测方法。对接收信号建模时采用目标能量泄漏采样模型以弥补泄漏损失，同时利用了干扰协方差矩阵的斜对称特性以降低对辅助数据的需求量，最终基于修正的两步GLRT准则设计出MPM-AMF-PHE检测方法。仿真结果表明，所提出的方法具有更优良的目标检测与距离估计性能，当辅助数据数量受限时，性能优势更为突出。未来的研究拟将上述框架扩展到非高斯干扰背景或存在有源干扰的情形。