局部腐蚀方中空夹层钢管混凝土偏压性能研究

2021-10-22李吉人王庆利殷炳帅

结构工程师 2021年4期

廖栩李吉人王庆利殷炳帅

（1.辽宁科技大学土木工程学院，鞍山114000；2.中铁建设集团有限公司，北京100043）

0 引言

钢管混凝土将钢材抗拉与混凝土抗压的优点充分结合，极大提高了结构的承载能力，在实际工程领域已得到广泛运用。对于钢管混凝土海洋平台或码头结构，“浪溅区［1-2］”长期受到海水与空气的共同腐蚀，该部位径厚比增大导致外钢管约束效应较其他部位明显降低，直接影响该类构件受力性能。Ahmed 等［3-4］以内外钢管宽厚比等作为参数，分析了中空夹层钢管混凝土短柱偏压下的局部屈曲，并建立了基于纤维单元的数学模型用于模拟该类构件局部屈曲行为。李吉人等［5-6］对高桩码头结构桩体内弯矩-轴力（M-N）相关曲线及弯矩-曲率关系滞回曲线进行对比，对塑性铰的开展空间进行了深入分析。文献［7］分析了薄壁中空夹层钢管混凝土偏压下的失效形式及加强筋的利用率对不同长细比构件延性的影响规律，并分析了三种不同类型的加劲肋对外钢管局部屈曲的影响。

黄宏、陈梦成等［8-10］对酸雨腐蚀工况下外钢管与内部混凝土的协同作用进行了分析，并针对腐蚀程度对结构弹性模量及刚度退化的影响，提出了更优化的钢管壁厚折减计算方法。韩林海、花幼星等［11-13］以荷载比与腐蚀深度为参数，分析了长期组合荷载的传递机制，提出了长期荷载作用下钢管混凝土梁柱的简化设计方法。王志滨等［14-16］对中空夹层薄壁钢管混凝土进行了有限元分析及偏压试验，通过分析长细比、径厚比及材料强度对荷载-弯矩相关曲线形状的影响，提出了该类构件在偏压荷载下的承载力简化计算公式。高山等［17-18］对海洋大气腐蚀环境下的空心钢管混凝土与实心钢管混凝土短柱进行了轴压试验，发现破坏模式随着腐蚀率的增加由剪切型向腰鼓型转换。目前国内外已开展大量锈蚀钢管混凝土力学性能研究，然而研究成果主要针对外钢管整个表面均受腐蚀的情况，如酸雨腐蚀、盐雾腐蚀等。局部腐蚀由于蚀坑的特殊性直接影响到结构的力学性能，同时腐蚀位置对结构弹性及塑性阶段的变形均有较大影响，故局部腐蚀下的钢管混凝土力学性能研究具有重要意义。

本文以局部腐蚀的腐蚀率、构件长细比、荷载偏心率及蚀坑纵向高度为参数，分析了外钢管约束效应对临界腐蚀率的影响，并通过蚀坑区域夹层混凝土纵向应力的变化分析了该部位受力全过程的荷载传递机理。

1 有限元模型的建立

1.1 模型设计

共设计19 个有限元分析模型，截面形式均采用外方内圆中空夹层，如图1 所示，内钢管直径Di均为120 mm，厚度ti均为1.5 mm。外钢管边长Bo均为200 mm，各模型长度L及外钢管厚度to见模型参数表（表1）。

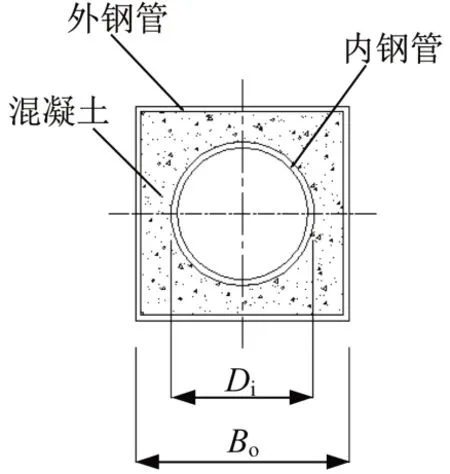
图1 方中空夹层钢管混凝土截面Fig.1 Cross section of square CFDST

各模型截面尺寸Bo及Di不变，进行长细比计算时，蚀坑所造成截面尺寸的差异可忽略不计，其长细比通过长度L确定，根据以下公式计算：

式中：L为模型长度；i为截面回转半径。

方中空夹层钢管混凝土截面回转半径根据以下公式计算：

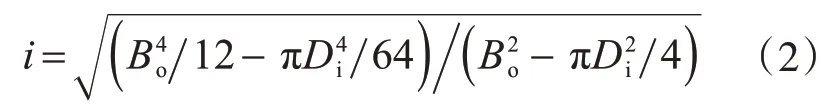
局部腐蚀方中空夹层钢管混凝土蚀坑位置如图2所示，蚀坑位置h为蚀坑中心沿柱的纵向高度（mm）。将实际海港结构桩体浪溅区高度进行缩尺后，各模型的腐蚀区域长度l均设置为150 mm。荷载偏心距e为加载点到截面中心的距离（mm），具体各项参数见表1。

表1 模型参数表Table 1 Model parameter table

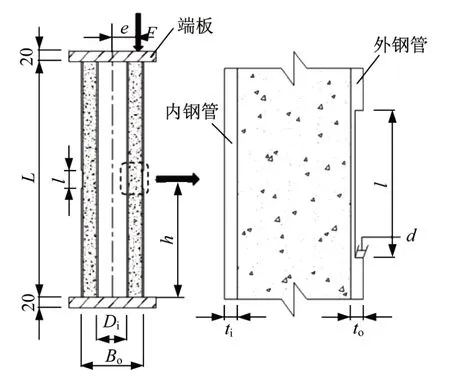
图2 局部腐蚀示意图Fig.2 Schematic diagram of local corrosion

腐蚀率根据文献［19］提出的外钢管质量损失率ηw进行计算，其表达式如式（3）所示：

式中：Go表示蚀坑区域未腐蚀前原有体积；G表示蚀坑体积，通过蚀坑深度d确定。

图3 为本文数值模拟与已有试验结果的对比，试验结果与本文数值模拟结果吻合较好。数值模拟结果偏于安全，误差均在10%以内，表明数值模型能较好模拟结构受力性能。

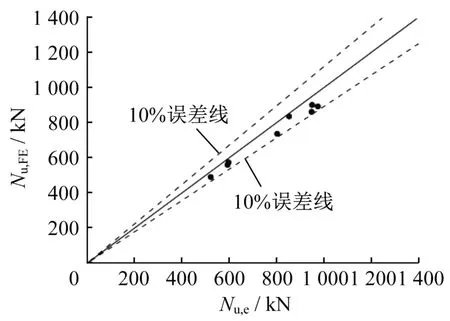
图3 试验值与数值模拟结果对比Fig.3 Comparison of compression capacity between test and numerical simulation results

1.2 材料性能

模型中内外钢管材料均采用Q345钢，屈服强度fy为345 MPa，本构关系模型采用文献［20］中五段式二次塑流模型。弹性阶段的弹性模量Es取210 GPa，泊松比μs取0.3。计算时将端板刚度设为无限大以保证不发生变形。

夹层混凝土强度等级为C30，立方体抗压强度为30 MPa。本构关系采用文献［20］中方截面外钢管约束混凝土本构关系，应力-应变曲线如图4 所示，其初始弹性模量通过Ec=4730fc计算，其中fc为混凝土轴心抗压强度。

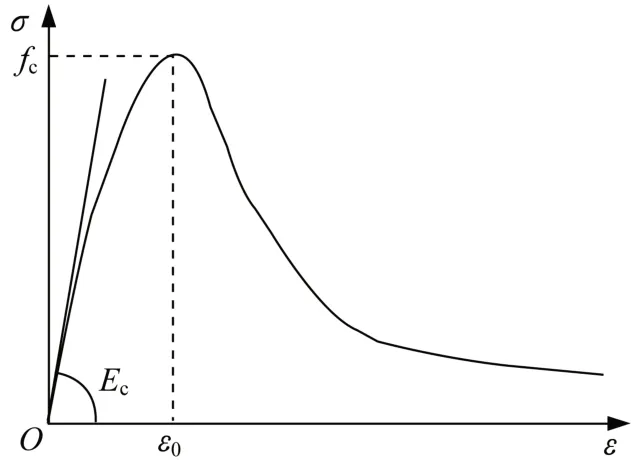
图4 混凝土应力-应变曲线Fig.4 Concrete stress-strain curve

本构关系表达式如下：

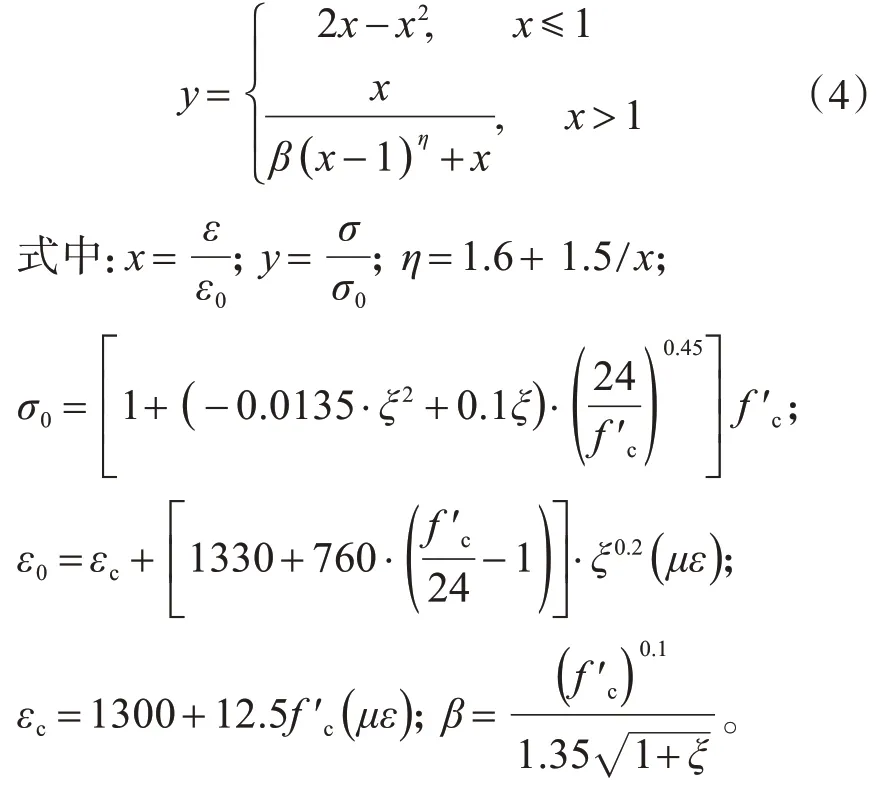
式中：ξ为约束效应系数，通过计算；fy为钢材屈服极限；fck为混凝土轴心抗压强度标准值，N/mm2；As为外钢管截面面积mm2；Ace为外钢管包裹的内部结构截面面积mm2。

计算ξ时考虑腐蚀区域与其他截面外钢管厚度不同，故对模型中腐蚀区域与其他截面的混凝土分开赋予材料属性。

1.3 模型建立

盖板、内外钢管和混凝土均采用八节点减缩积分格式的三维实体单元（C3D8R）［19］。进行网格划分时，为了提高计算效率并保证计算的准确性，端板与内外钢管不相连的部位网格较大，其余部位的网格尺寸较小，考虑到模型的塑性变形主要集中在腐蚀区域，因此在将腐蚀区域的网格进行了细化，有限元分析模型如图5所示。

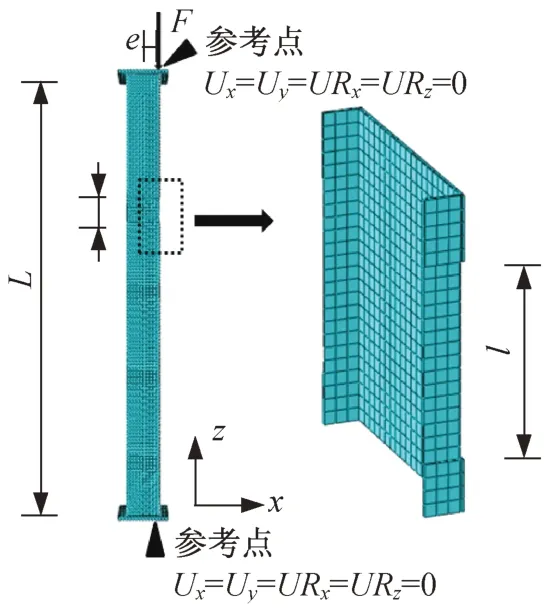
图5 有限元分析模型Fig.5 Finite element analysis model

盖板与内外钢管间的相互作用采用绑定（tie），以保证钢管与盖板的位移变形一致。底部约束三个方向的平动位移及竖向（Z向）与偏心方向（X向）的转动，加载端约束水平向的平动位移及竖向（Z向）与偏心方向（X向）的转动。钢管与混凝土之间的法向接触采用“硬”接触，切向库伦摩擦系数为0.6，将钢管面设置为主面，混凝土面设置为从面。采用位移加载时考虑到腐蚀区域刚度小，变形集中在腐蚀区域，故在Z向施加位移荷载600 000με，其中1με的长度为l/106（mm）。

2 极限承载力分析

2.1 荷载-跨中挠度曲线

为研究腐蚀率ηw、长细比λ及荷载偏心距e对极限承载力的影响，提取各模型荷载-跨中挠度曲线如图6 所示。进行承载力分析时，不考虑蚀坑位置（蚀坑中心沿柱纵向高度）的影响，故只取蚀坑位于跨中的结果进行分析。

图6 各参数对荷载-跨中挠度曲线的影响Fig.6 The influence of various parameters on N-U curves

对比表明，腐蚀率ηw、长细比λ及荷载偏心距e对弹性阶段刚度及承载力均有显著影响，对于L=2 700 mm 的构件，当ηw=80%时，承载力已降为非腐蚀工况的51%。主要原因在于蚀坑区域外钢管厚度减小导致对内部结构的约束效应降低，蚀坑较早产生局部屈曲。当ηw及λ不变时，弹性阶段刚度及承载力随着e的增大而明显减小。相较于腐蚀率及荷载偏心率，长细比对承载力的影响较小，但随着长细比的增大，偏心荷载产生的轴向二阶效应明显，导致弹性阶段刚度降低，同时峰值荷载对应的跨中挠度明显增大。

2.2 挠度开展曲线

当构件截面尺寸沿纵向高度不变时，若构件两端采用铰接，最大弯矩出现在跨中。若局部腐蚀的ηw较大时，蚀坑区域在加载过程中会出现明显的应力集中，造成该处变形明显增大，图7 为蚀坑位于不同高度时，L=2 700 mm 的模型在两种不同腐蚀率下的挠度曲线，图中纵坐标为试件高度，横坐标为横向挠度。

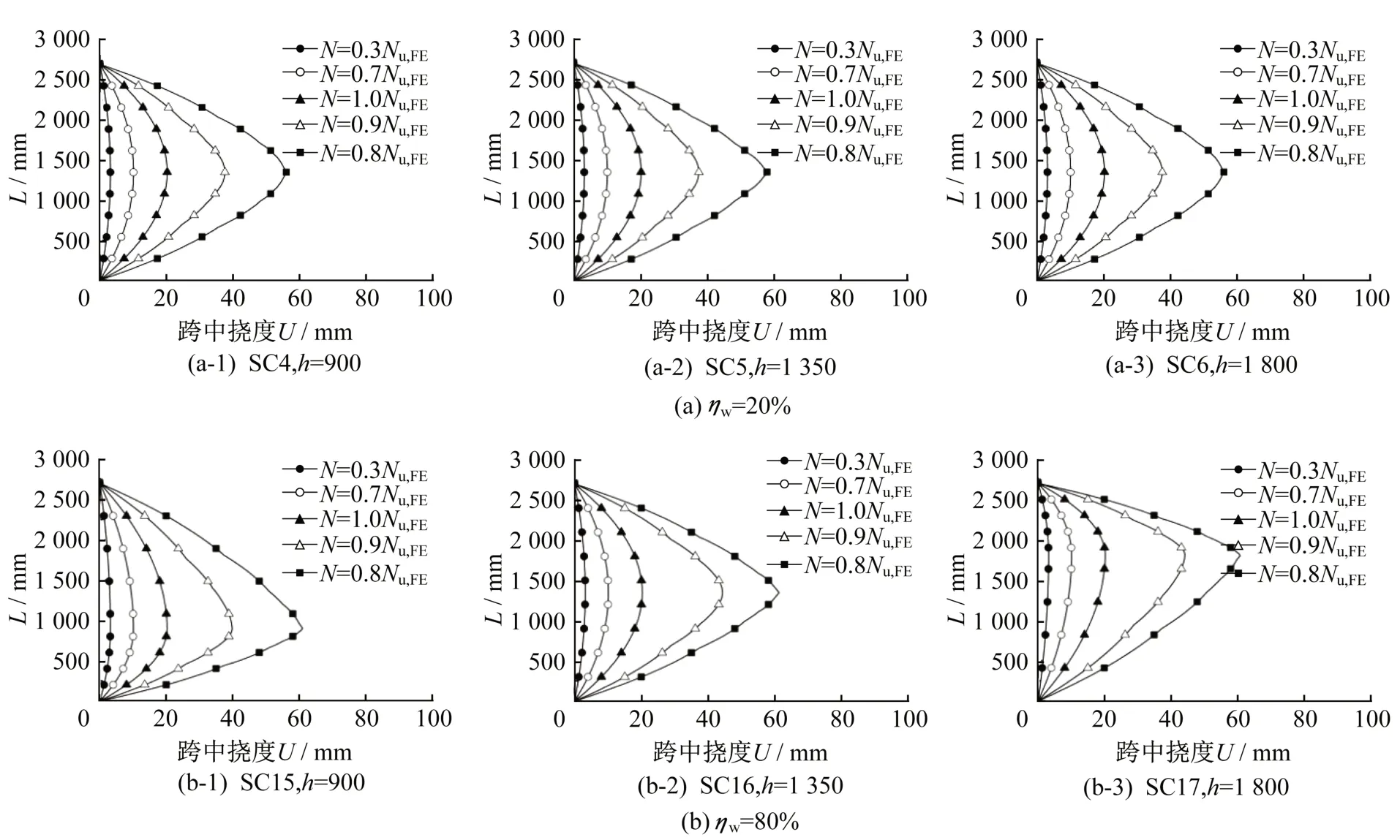
图7 蚀坑位置对变形的影响Fig.7 The influence of the location of the pit on the deformation

对比表明，当ηw=20%时，蚀坑位于不同高度时构件最大挠度均出现在跨中，并且蚀坑外置的改变对受力全过程挠度开展曲线影响甚微；当ηw=80%时，蚀坑区域外钢管相较于其他部位较早产生变形，且随着荷载的增加，横向挠度最大值自始至终均出现在蚀坑处。同时，相同荷载下的横向最大挠度值相近。当蚀坑区域钢管屈服以后，对于仍处于弹性范围内的非腐蚀部位变形得以恢复，非腐蚀部位各截面弯矩减小，故挠度曲线逐渐由“圆弧形”过渡到“折线形”。

2.3 临界腐蚀率

当蚀坑位于构件跨中时，无论ηw值为多少，挠度最大值均出现在跨中。若蚀坑不在跨中，当外钢管采用不同厚度或改变外钢管强度，总会存在某一临界腐蚀率ηcw，当ηw＜ηcw时，挠度最大值出现在跨中，当ηw＞ηcw时，挠度最大值出现在蚀坑区域。针对L=2 700 mm 的试件，图8（a）为当外钢管采取1 mm、1.5 mm、2 mm、2.5 mm、3 mm 五种厚度时的临界腐蚀率，当fyo分别取235 MPa、298 MPa、345 MPa、400 MPa、450 MPa、500 MPa、550 MPa 时的临界腐蚀率如图8（b）所示。

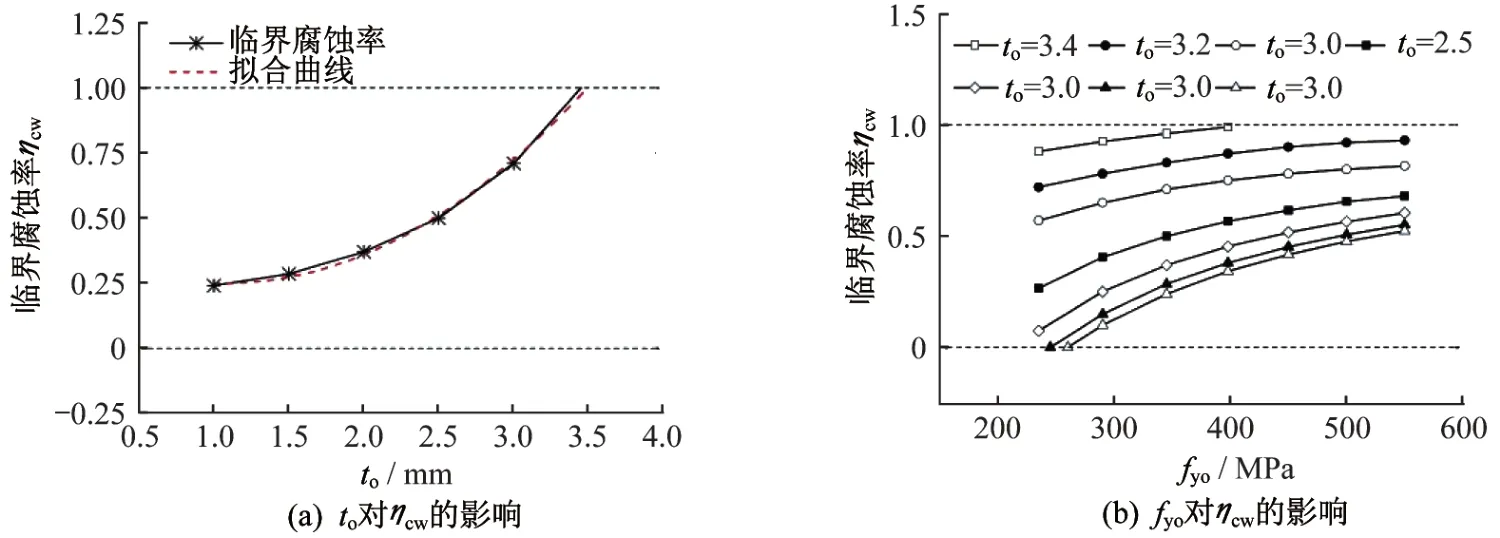
图8 临界腐蚀率ηcwFig.8 Critical corrosion rate ηcw

临界腐蚀率ηcw随着外钢管厚度to及外钢管强度fyo的增加而增加，介于0～1之间。ηcw与外钢管厚度to的关系呈二次函数关系，与fyo近似呈线性关系，且to的值越大，ηcw与fyo的关系越近似为一条直线。与约束效应系数ξ与外钢管强度及厚度的影响一致。蚀坑区域约束效应系数ξ通过以下公式计算：

式中：Asa为外钢管蚀坑区域腐蚀后剩余截面面积［13］；Ace为蚀坑区域外钢管所包含的内部结构截面面积。

局部腐蚀方中空夹层钢管混凝土蚀坑区域外钢管截面面积通过以下公式确定：

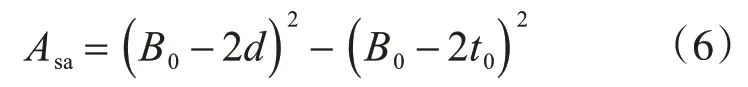
可见造成构件最大挠度位置发生改变的临界腐蚀率ηcw的主要影响因素为外钢管的约束效应。当ηw＜ηcw时，蚀坑区域外钢管约束效应降低，蚀坑截面出现应力集中，但不足以影响偏压荷载产生的弯矩，故无论腐蚀位置在多少高度，最大弯矩均出现在跨中；当ηw＞ηcw时，蚀坑区域外钢管对内部结构约束效应明显降低，随着荷载的增加，混凝土横向变形迅速开展，导致全构件危险截面并不位于跨中，而位于蚀坑截面。

3 破坏机理分析

3.1 荷载-环向应变曲线

为研究不同参数对局部腐蚀方中空夹层钢管混凝土偏压过程中的荷载传递机理，提取不同参数下的荷载-环向应变曲线进行对比如图9 所示。图中采用黑色填充的曲线为远离加载点一侧的蚀坑表面中心处的环向应变值。无填充曲线为靠近加载点一侧的蚀坑表面中心处的环向应变值对比表明，当e及λ不变时，靠近加载点一侧环向应变极限值受ηcw影响不大，如图9（a）所示。且远离加载点一侧蚀坑环向应变由“拉”到“压”的过渡现象受ηcw影响较小。当ηcw及λ不变时，如图9（b）所示，若偏心距较小，蚀坑区域钢管在弹性范围内全截面环向受拉，近加载点一侧屈服产生较大变形后，远离加载点一侧开始出现压应变。若偏心距较大时，远离加载点一侧自始至终只出现环向压应变。

图9 荷载-环向应变曲线对比Fig.9 Comparison of load-circumferential strain curves

3.2 夹层混凝土纵向应力云图

由本文 2.3 可知，当ηw＞ηcw时，最大挠度会出现在蚀坑处，为研究此工况下受力全过程夹层混凝土纵向应力分布，提取A 点（0.5Nu，完全弹性）；B 点（构件达到极限承载力）；C 点（荷载下降到极限承载力的80%）的夹层混凝土纵向应力云图，同时将蚀坑中心截面（1-1 截面）与构件跨中截面（2-2 截面）进行对比。模型尺寸参数采用表1 中SC18，ηw调整至75%，分析采用的蚀坑高度调整为h=3 075 mm，图10中单位为MPa。

对比表明，受力全过程跨中截面夹层混凝土纵向应力始终小于蚀坑中心截面，且对于蚀坑区域以外的截面，受力全过程纵向应力均未达到C30混凝土抗压极限承载力值。对比图10中所取两处截面的变形发现，蚀坑中心截面由于约束效应较小，达到承载力后出现明显的变形，受压区混凝土横向扩张。如图10（c）所示，1-1 截面（蚀坑中心截面）混凝土已明显扩张到屈服前外侧边缘（图中黑色虚线）以外。而跨中截面在受力全过程截面均处于正方形状态。当构件屈服后，两处截面受拉区纵向拉应力均有小幅度降低，且受力全过程蚀坑中心截面受拉区面积均大于跨中截面。

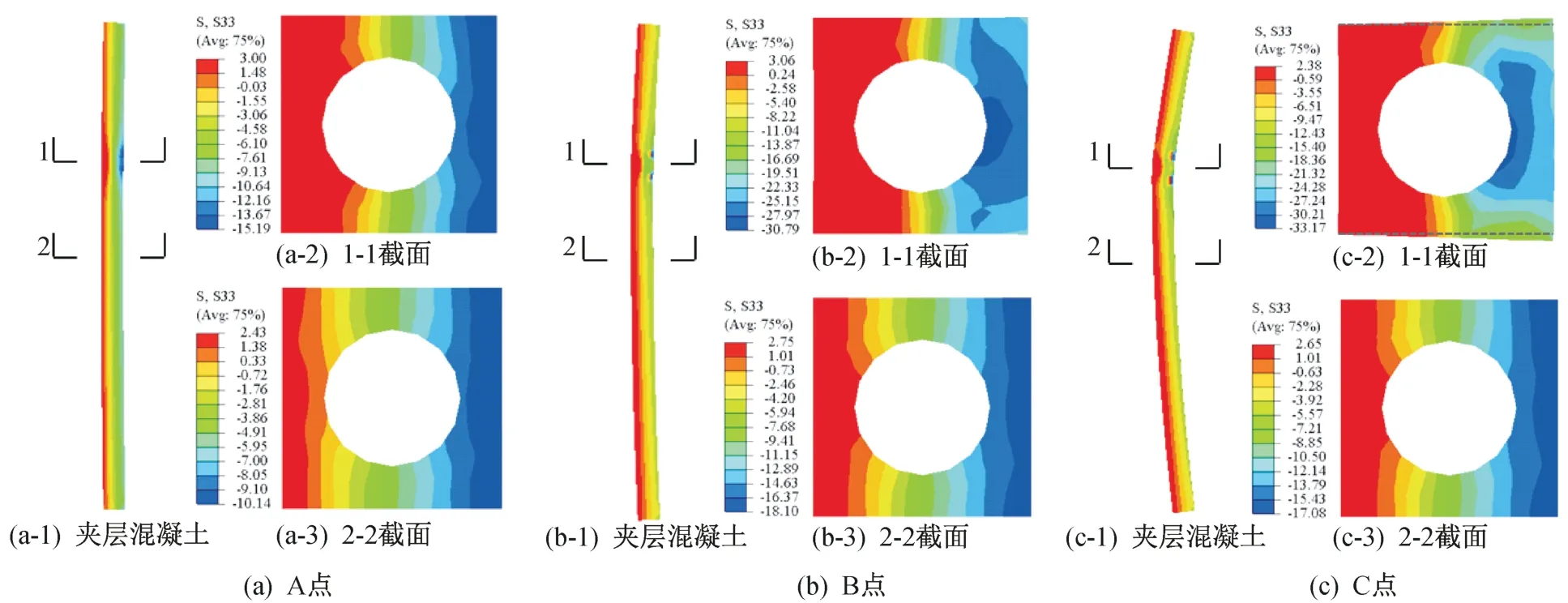
图10 混凝土纵向应力分布Fig.10 Longitudinal stress distribution of concrete

3.3 蚀坑应力云图

为研究局部腐蚀的腐蚀率对构件整体变形及蚀坑区域局部屈曲的影响，图11（a）为将SC17 模型中ηw调整至30%的计算结果，与图11（b）（ηw=80%）的计算结果进行对比，图中单位为MPa。

对比表明，ηw对结构整体变形影响显著，当ηw＜ηcw，构件整体变形的挠度曲线较圆滑，虽然蚀坑区域外钢管应力最大值大于其他部位，但其局部屈曲的现象不明显。当ηw＞ηcw时，如图11（b）所示，蚀坑区域挠度较其他截面明显增大，蚀坑区域外钢管局部屈曲现象严重，出现明显的堆叠现象，且蚀坑以外的截面受力全过程外钢管处于完全弹性阶段。

图11 腐蚀率ηw对局部屈曲的影响Fig.11 The effect of ηw on local buckling

4 承载力简化计算

对于外钢管局部腐蚀下的钢管混凝土承载力公式的相关研究不多见，且该类工况在海洋平台结构中出现较多，故有必要提出局部腐蚀方中空夹层钢管混凝土承载力简化计算公式。文献［20］中提出了考虑长细比的钢管混凝土承载力计算公式如下：

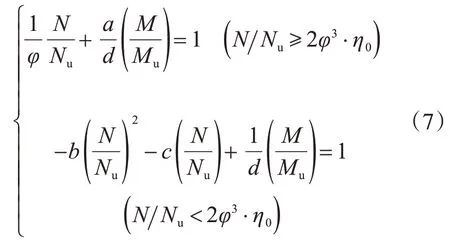
相关曲线平衡点的横纵坐标值ζ0与η0分别按式（8）、式（9）计算：

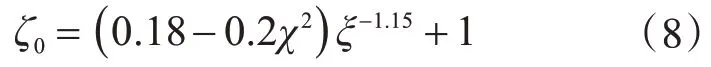
式中：约束效应系数ξ采用式（5）计算；局部腐蚀方套圆中空夹层截面形式钢管混凝土的空心率χ通过计算。

对于式（7）中考虑长细比的轴压稳定系数φ通过以下公式计算：

式中：局部腐蚀方中空夹层钢管混凝土发生弹性失稳的界限长细比通过计算，发生塑性失稳的临界长细比通过λp=计算。

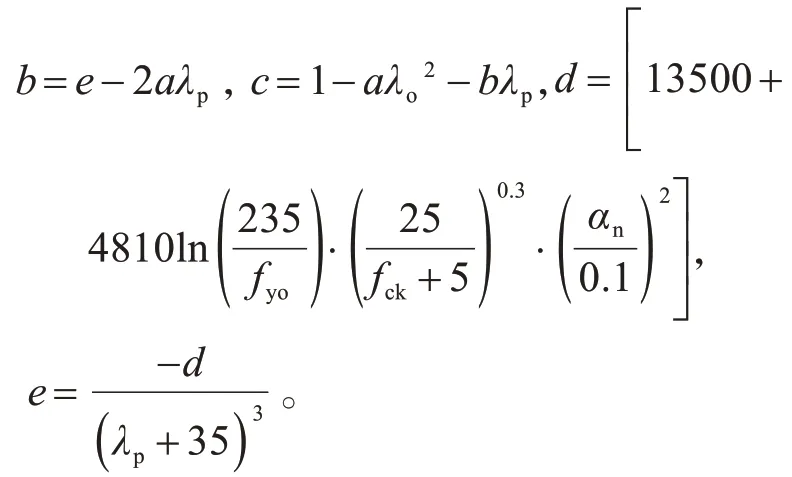
式中，fyo与fck的单位均为 N/mm2。

式（7）中轴压强度承载力根据Nu=Nosc，u+Ni，u计算，内钢管极限承载力通过Ni，u=fyiAsi计算，外钢管与混凝土的极限承载力考虑外钢管的约束效应，采用以下公式进行计算：

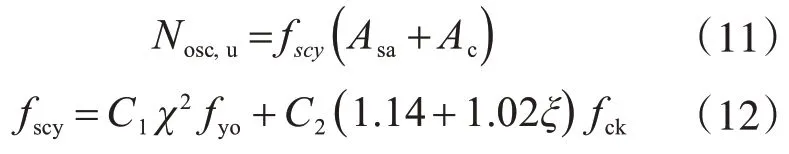
式中：Asa为外钢管腐蚀后剩余截面面积，通过本文式（6）计算；Ac为混凝土截面面积，C1通过C1=计算，C2通过计算；α与αn分别为含钢率与名义含钢率，通过α=计算，Ace为腐蚀区域外钢管包含的内部截面面积。

式（7）中抗弯承载力Mu按照以下公式计算：

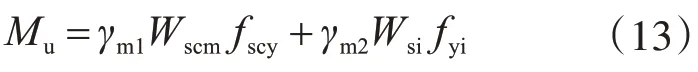
系数γm1与γm2分别按照以下公式计算：

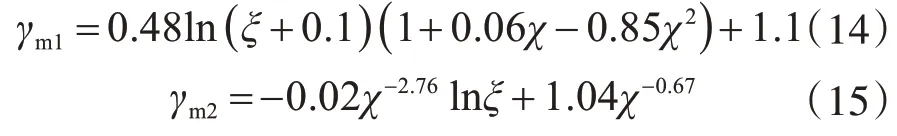
式（13）中Wscm为蚀坑区域外钢管与混凝土的截面抗弯模量，当蚀坑位置不在跨中且ηw＜ηcw时通过式（16）计算，其他情况通过式（17）计算：

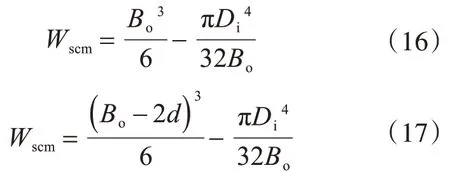
内钢管截面抗弯模量通过以下公式计算：

上述计算方法是对已有的方中空夹层钢管混凝土偏压承载力简化计算公式的部分参数进行了修改，主要包括在不同腐蚀率下截面抗弯模量的计算、约束效应系数的确定等，最终建议以此作为局部腐蚀条件下中空夹层钢管混凝土偏压承载力计算公式。在计算轴压承载力与抗弯承载力时，若ηw＞ηcw，外钢管截面积则考虑采用腐蚀区域外钢管面积，即将整体结构当作外钢管边长为Bo-2d的方套圆中空夹层钢管混凝土考虑，故计算结果偏安全。