超大跨径组合梁斜拉桥稳定和极限承载力研究

易岳林 陈 政 王雨阳 周子杰

（1.安徽省交通控股集团有限公司，合肥230000；2.同济大学，上海200092）

0 引 言

斜拉桥结构由于独特的缆索承重结构，在大跨径桥梁中应用广泛。目前，国内外已有多座超千米的斜拉桥被设计建造。随着跨径的增加，斜拉桥整体的稳定性和极限承载力成为控制设计的因素之一。于向东等［1］针对斜拉桥索塔的弹性稳定采用能量法进行理论分析，并对洞庭湖三塔斜拉桥中塔的稳定性进行分析。罗晓峰等［2］提出了修正的弹性支承法计算斜拉桥桥塔稳定性，并应用于苏通大桥桥塔稳定性计算。郭卓明等［3］推导了独塔斜拉桥结构体系的弹性和弹塑性稳定性的简化分析方法。李兆香等［4］基于能量变分原理推导了大跨度斜拉桥面内稳定的计算公式，并应用于青州闽江大桥计算。施志雄等［5］分析了施工误差对大跨斜拉桥自己先承载力的影响。随着计算机的发展，数值计算成为近年来大型复杂斜拉桥性能分析的主要手段。顾安邦等［6］介绍了考虑拉索只受拉特性、材料和几何非线性的有限元分析方法，并应用于某双塔斜拉桥稳定性分析。

组合梁斜拉桥是斜拉桥结构中的一种形式。是1980 年德国桥梁设计师Leonhardt 在美国Sunshine Skyway Bridge 投标方案中提出。采用混凝土板替换钢箱梁顶板，利用混凝土良好的抗压性获得良好的经济性。2015年石兆敏等［7］研究了大跨组合梁斜拉桥的静力性能。2018 年，赵人达等［8］采用有限元方法分析了某360 主跨的组合梁斜拉桥在施工和成桥运营阶段的弹塑性稳定性。邹建波等［9］进一步分析了斜拉索初始缺陷、主梁钢结构强度、混凝土桥塔强度等结构参数对大跨度组合梁斜拉桥弹性塑性稳定性的影响。2019年，王岭军［10］采用有限元方法分析了某主跨436 m组合梁斜拉桥在施工和运营过程中的弹性稳定性。

望东长江公路大桥采用了主跨638 m 的PK型组合梁斜拉桥结构形式，是目前我国最大跨径的组合梁斜拉桥。本文采用数值有限元分析方法，对这一超大跨径的组合梁斜拉桥的整体稳定性进行研究分析。研究成果可为同类工程提供参考。

1 结构信息

安徽省望东大桥为国家高速公路网G35的跨长江通道，是“纵四”商丘—景德镇公路的重要组成部分，是沟通安徽省西部地区的纵向干线公路。

望东大桥跨径布置为（78+228+638+228+78）m，全长1250 m，主桥为双塔双索面半漂浮体系斜拉桥，如图1 所示。主梁采用PK 型分离双箱组合梁型式，组合梁全宽35.2 m，不设风嘴，梁高3.5 m（组合梁中心线处），其中钢梁中心线处梁高3.106～3.226 m。

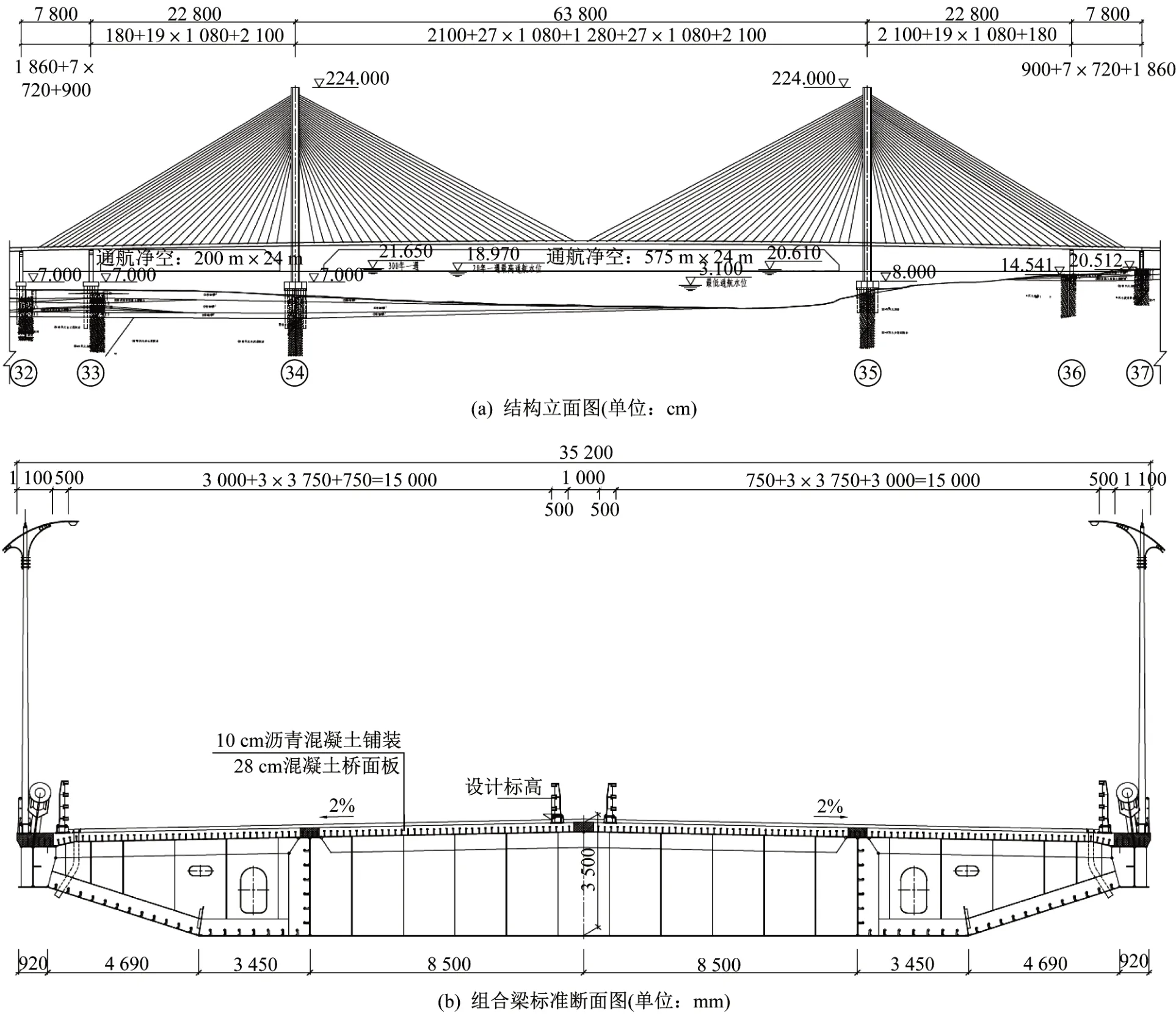
图1 望东大桥结构布置图Fig.1 Layout of Wangdong Yangtze River Bridge

主塔为钻石形桥塔，桥面以上为倒Y 形。索塔处设置竖向支座、横向抗风支座，纵向设置2 个E 形动力耗能装置，全桥共4 个，辅助墩设置竖向弹性支座，过渡墩处设置竖向支座、横向抗风支座。

2 弹性稳定承载力

弹性稳定承载力是在不考虑材料非线性、几何非线性等因素下，结构保持稳定的最大载荷，又被称为一类稳定或者欧拉稳定承载力。弹性假定下结构的临界状态平衡方程表示为

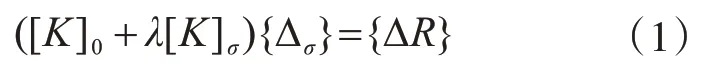
式中，[K]0和λ[K]σ分别为单元弹性刚度矩阵和单元几何刚度矩阵。对于固定的结构，式中的单元刚度矩阵[K]0是定值。[K]σ是分析工况对应标准荷载下的单元几何刚度矩阵，对于给定的荷载工况是定值。上述方程转变为求解临界状态对应的几何刚度矩阵放大系数λ，即在λ倍标准荷载下结构达到临界平衡状态。

目前，我国斜拉桥设计规范采用弹性稳定安全系数指标λ来评价结构体系的整体稳定和安全性。《公路斜拉桥设计细则》（JTG D65-01—2007）［11］规定我国 800 m 以下的公路斜拉桥，斜拉桥结构的弹性稳定安全系数不应小于4.0。

2.1 分析参数

望东长江大桥主桥组合梁采用Q345C 钢材和C55 混凝土桥面板，桥塔采用C50 混凝土，斜拉索采用1860钢绞线。主要构件的材料特性如表1所示。

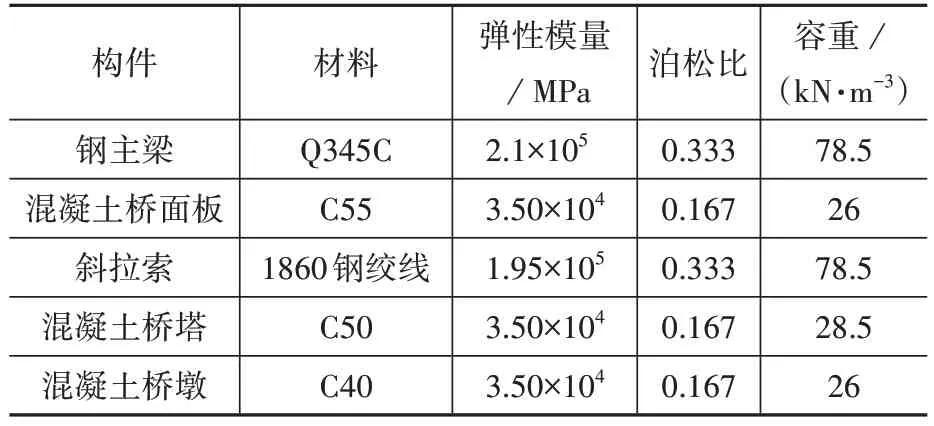
表1 弹性稳定分析材料参数Table 1 Material parameters of elastic stability analysis

采用通用有限元软件ANSYS 建立空间三维鱼骨梁模型。主梁、主塔采用beam188单元模拟，主梁节点和斜拉索吊点用刚臂连接，采用beam188 单元模拟，斜拉索采用link8 单元模拟，过渡墩、辅助墩、临时墩通过采用支座处施加竖向及水平约束模拟。有限元模型如图2所示。

图2 弹性分析有限元模型Fig.2 Elastic finite element models

研究针对施工和运营阶段的关键工况进行结构体系的弹性稳定性分析。其中，大跨度组合梁斜拉桥在施工过程有三个关键的阶段，包括即裸塔阶段、最大双悬臂阶段、最大单悬臂阶段。各个阶段分别考虑按照环境风场确定的设计最大风速37.15 m/s，并按照风向顺桥向和纵桥向分别考虑。施工阶段分析工况共计9 个。成桥阶段典型工况包括恒载和不同汽车荷载模式的组合，汽车荷载包括全桥满布荷载、半桥满布荷载、边跨满布荷载和中跨满布荷载。其中恒载和全桥满布荷载进一步与纵横向的最大风荷载进行组合。成桥阶段分析工况共计10 个。施工及成桥恒载工况下的稳定系数基数为标准恒载，运营阶段组合活载工况下的稳定系数仅为活载的倍数（恒载系数为1）。

2.2 施工阶段弹性稳定性

施工阶段弹性稳定计算结果汇总如表2 所示。对比计算结果可知：在施工过程中，有风或者无风工况对裸塔状态下结构弹性稳定系数有一定影响，但是影响程度不大；最大双悬臂状态，主梁悬臂不是很长，主梁承受的轴向压力不大，而桥塔受到斜拉索索力影响承受很大压力，索塔“梁—柱”效应明显，屈曲模态表现为主塔的顺桥向失稳，且此阶段弹性稳定系数受索力影响较为明显；最大单悬臂状态，由于辅助墩的设置和边跨的合龙，虽然悬臂长度有所增加，但是总体来说结构的稳定性有一定的提高，屈曲模态表现为主梁的竖平面弯曲。此外，施工阶段结构的稳定性受横桥向风荷载的影响相对于顺桥向风荷载的影响要大。

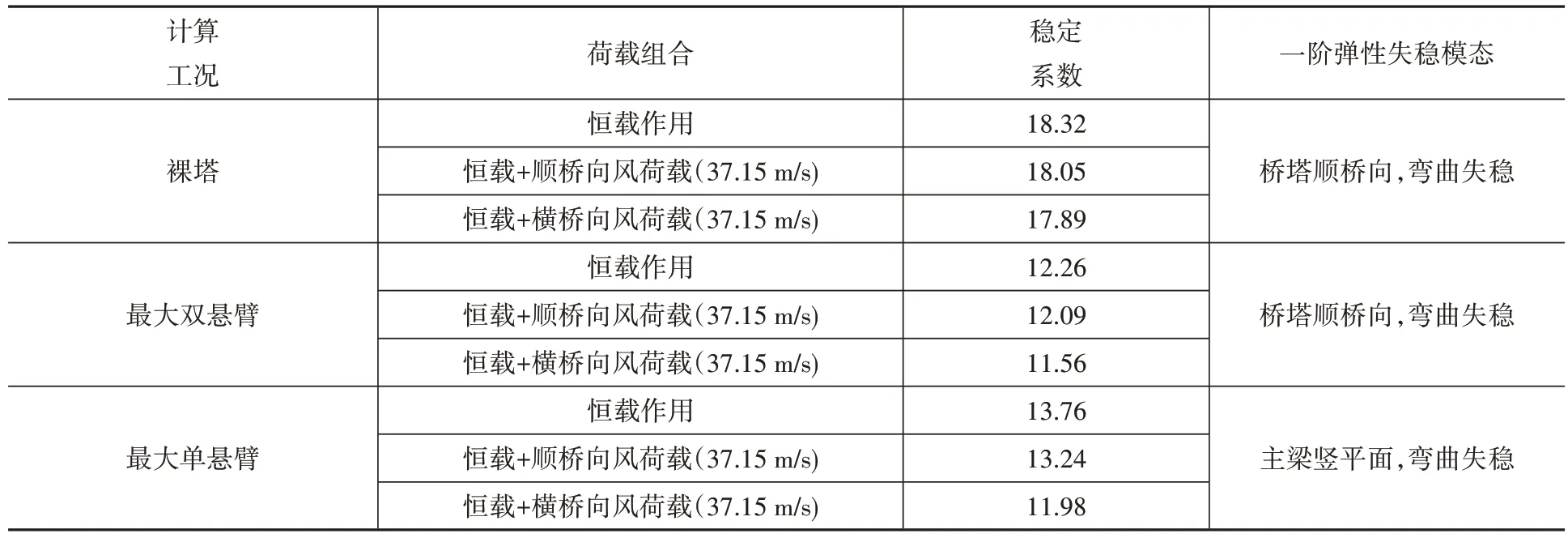
表2 组合梁斜拉桥施工阶段弹性屈曲稳定性能分析结果Table 2 Elastic buckling stability of composite beam cable-stayed bridge during construction stage

2.3 运营阶段弹性稳定性

运营阶段计算结果汇总如表3 所示。计算结果表明，恒载作用下望东大桥的一阶弹性稳定系数为9.470。在全桥满布汽车荷载作用下，失稳形式包括全桥面外失稳和局部失稳。一阶稳定系数为8.794。与恒载工况相比，增加活荷载作用时，主梁的承载能力减低，主梁的稳定成为控制结构稳定安全的第一因素。由于背景工程边跨的刚度较中跨大，中跨的失稳首先出现。

表3 组合梁斜拉桥运营阶段弹性屈曲稳定性能分析结果Table 3 Elastic buckling stability results of composite beam cable-stayed bridge during operation stage

3 弹塑性承载力

弹塑性承载力考虑材料非线性和几何非线性因素，在荷载作用下构件截面材料屈服，体系形成一个或多个塑性铰，导致结构的整体刚度降低，在某一临界荷载下丧失进一步承担荷载的能力，又被称为二类稳定。这一承载力理论上比弹性承载力更接近结构的实际承载力。在结构弹塑性分析中，结构平衡方程表达为

式中，[K]L为大位移矩阵，结构在不断增加的外荷载的作用下，结构刚度不断发生变化，当外荷载产生的应力使得结构切线刚度矩阵趋于奇异时，结构就达到了承载能力极限。

《公路斜拉桥设计细则》规定［11］，混凝土主梁斜拉桥的弹塑性强度稳定安全系数不应小于2.5，钢主梁斜拉桥不应小于1.75。

3.1 分析参数

混凝土材料本构关系采用Rüsch 模型。Q345C 采用双折线模型描述材料的本构关系，初始弹性模量Ec=2.10×105MPa，屈服应力345 MPa；高强钢材本构关系采用三折线模型，拉索初始弹性模量取根据Ernst 公式修正的弹性模量Ec′，钢材屈服应力取0.93 倍抗拉强度标准值0.93ftk=1 730 MPa。材料采用多段线性随动强化模型，以Von Mises 等效应力作为判断钢绞线是否进入塑性工作阶段的标准。各材料的应力-应变曲线如图3所示。

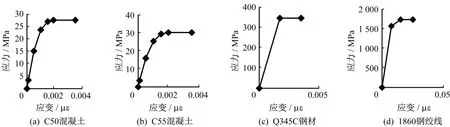
图3 弹塑性分析材料本构Fig.3 Material constitutive of elastoplastic analysis

采用通用有限元软件ANSYS 建立空间三维鱼骨梁模型。索塔及主梁采用空间梁单元Beam188 模拟，钢绞线及拉索采用空间杆单元Link8 模拟。拉索与主梁、拉索与索塔、主梁与横梁通过刚性约束连接。弹塑性模型如图4所示。

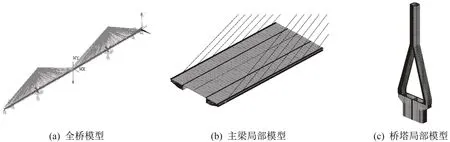
图4 弹塑性分析有限元模型Fig.4 Elastoplastic analysis finite element models

主跨638 m组合梁斜拉桥在施工过程中，分别考虑裸塔阶段、最大双悬臂阶段和最大单悬臂阶段。由于风荷载对施工过程中结构稳定性有一定的影响，研究中考虑了恒载、恒载+顺桥向风荷载以及恒载+横桥向风荷载三种荷载工况下的结构稳定性。

运营阶段，研究选取四种典型控制荷载工况进行分析，包括“恒载”、“恒载+全桥满布汽车荷载”、“恒载+百年一遇纵桥向风荷载”和“恒载+百年一遇横桥向风荷载”。

3.2 施工阶段极限承载力

有限元分析结果如表4 所示，分析结果表明，裸塔阶段不同荷载组合下结构弹塑性稳定系数约为8，结构最终破坏形态为主塔强度破坏；最大双悬臂阶段在上述荷载组合下结构弹塑性稳定系数约为5，结构最终破坏形态为主塔强度破坏；最大单悬臂阶段，结构弹塑性稳定系数约为4，结构最终破坏形态为主塔强度破坏。随着施工的进展、悬臂长度的增加，结构稳定性逐渐降低。

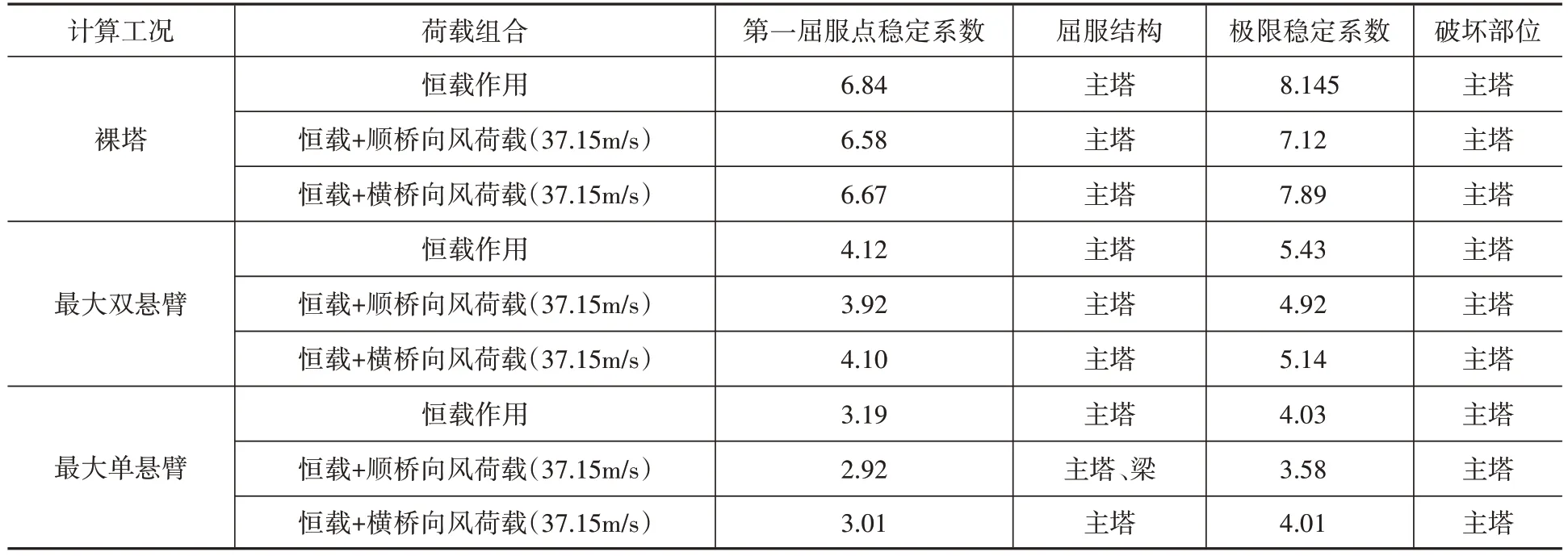
表4 组合梁斜拉桥施工阶段弹塑性稳定分析结果Table 4 Elastoplastic stability of composite beam cable-stayed bridge during construction stage

施工阶段，风对结构弹塑性稳定性影响比较显著，风荷载作用下结构有一定的初始偏位，引起二阶效应。对于各个施工阶段，有风荷载作用时结构弹塑性稳定性均较无风时有所减小；同时由于主塔顺桥向刚度小于横桥向刚度，顺桥向风荷载对结构的影响也大于横桥向风荷载作用。

三个施工关键工况最终破坏形态均为主塔达到强度破坏。可能破坏的位置为塔柱与下横梁交界处和主塔中上塔柱交接处，施工时需要注意，保证混凝土浇筑质量。

3.3 运营阶段极限承载力

采用跨中主梁竖向位移作为斜拉桥结构整体刚度的表征量，运营阶段“荷载系数——跨中主梁竖向位移”曲线如图5 所示。恒载为2.169，“恒载+全桥满布汽车荷载”为2.000，“恒载+百年一遇纵风荷载”为2.112，“恒载+汽车+纵风荷载”为2.169。

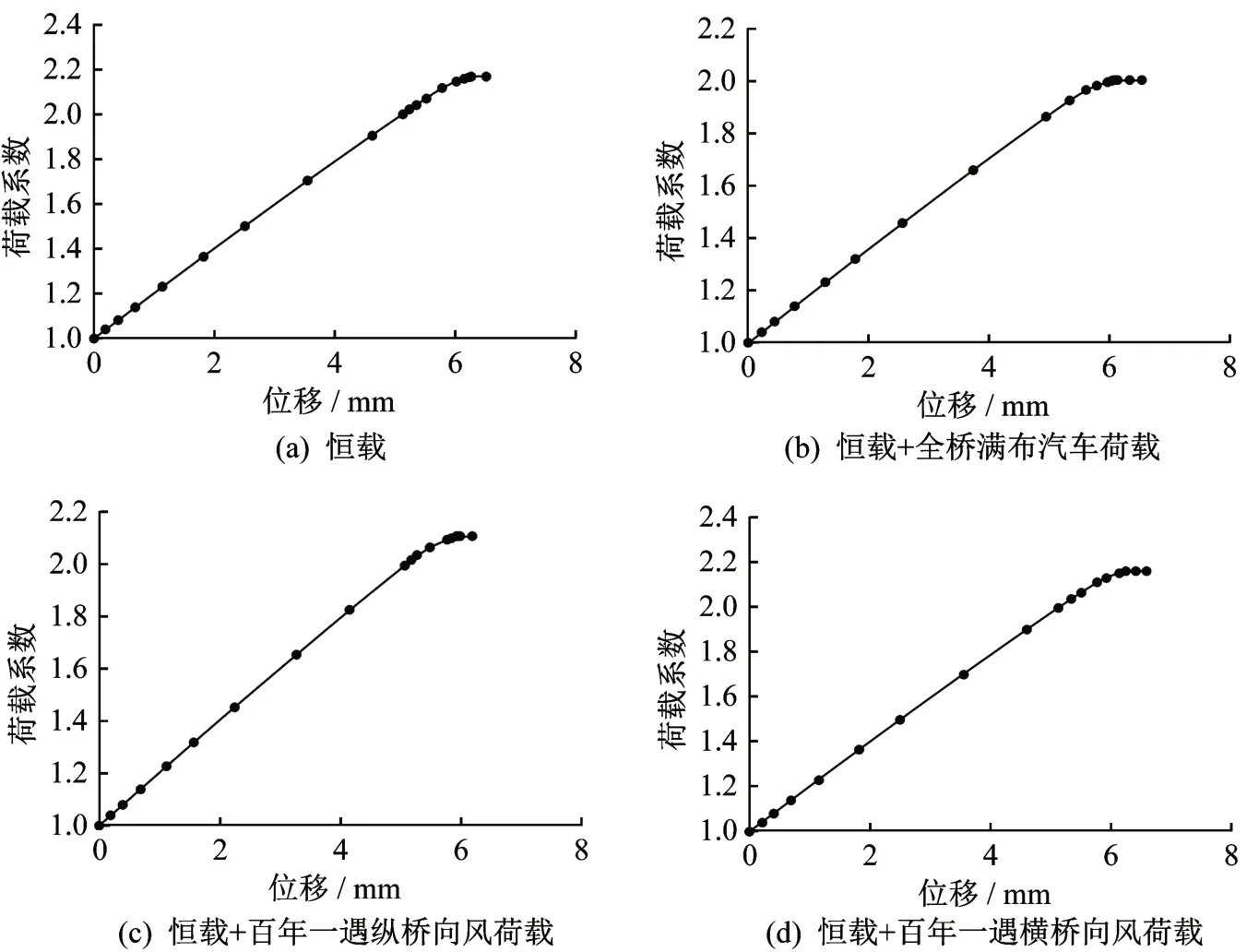
图5 荷载-位移曲线Fig.5 Load-displacement curves

恒载工况结构失效历程如图6 所示，荷载系数在1～1.905 时，结构处于弹性工作状态，刚度基本不变；当荷载系数达到1.905 时，桥塔附近处钢主梁底板部入塑性工作状态。当荷载系数达到2.07 时，索塔在上塔柱与中塔柱交界处产生塑性变形。当荷载系数增大至2.168 5 时，混凝土索塔在上塔柱与中塔柱交界处形成塑性铰；在桥塔附近处主梁底板较大范围内钢材屈服。作为斜拉桥的核心构件，索塔承载能力和主梁承载能力的丧失导致结构整体丧失承载能力，此时结构最大位移为主梁跨中下挠6.40 m，达到极限。

图6 恒载工况结构破坏历程Fig.6 Structural failure process under dead load condition

四种荷载组合下的结构破坏历程具有一致性，破坏均从主梁局部的屈服开始，然后主塔局部屈服，最终结构整体失效于钢主梁截面的屈服失稳和主塔节段屈服。计算结果表明，结构极限承载能力的控制因素为主塔和主梁的稳定问题。

4 结 论

针对主跨638 m 大跨组合梁斜拉桥的整体稳定和极限承载力研究表明：

（1）大跨组合梁斜拉桥设计时索塔刚度较大，一类稳定为主梁的竖向弯曲失稳，主梁的稳定问题成为控制结构整体稳定的因素；全桥满布汽车荷载是结构弹性稳定性最不利工况。

（2）结构体系完好状态下极限承载力中“恒载+全桥满布活载”是控制工况，其结构极限荷载系数为2.0，在结构的破坏历程中，主梁总是最先开始屈服，接下来是索塔在上塔柱与中塔柱交界处开始屈服，再然后是索塔在上塔柱与中塔柱交界处节段屈服，形成塑性铰，结构达到极限承载状态。

（3）研究中主跨638 m 组合梁斜拉桥在“恒载+全桥满布汽车荷载”工况下结构极限荷载系数为2.0，随着跨径的提升这一系数将进一步降低，此时可以通过设置约束或者提高材料强度来进一步实现跨径的提升。