单向板在任意曲线荷载作用下的弯矩分布计算与配筋设计

刘 伟 于 越 李遇春

（同济大学水利工程系，上海200092）

0 引 言

板是土木工程中常用的一种结构形式。在实际工程中，在板结构上常常作用有线荷载，板的结构设计需要分析线荷载作用下薄板上弯矩分布。谢 子 洋［1］、曾 大 明［2］基 于 Navier 解 法［3］，结 合MATLAB［4］和 ANSYS［5］有限元软件分析单向板主次方向弯矩分布关系。臧正义［6］采用基于最小势能原理的 Rayleigh-Ritz 法［7］分析对边简支板在线荷载作用下的弯矩。但该文分析的均为直线荷载作用下的单向板，而在实际工程中线荷载的形式复杂，甚至存在曲线形荷载。

当板结构上的线荷载为曲线荷载时，例如：铁路涵洞顶板上的铁路线为弧线时，楼板上砌筑曲线形的墙体时，板上的荷载均可以看成曲线荷载，在一般的结构计算手册以及常见的结构分析文献上难以查到曲线荷载作用下的板内弯矩计算公式，结构工程师需要采用通用商业软件来进行板的抗弯计算，然而在结构有限元计算中，曲线荷载的输入是一件相当麻烦的事情，需要耗费大量时间与精力。鉴于此，本文给出单向板在一般曲线荷载作用下的弯矩计算公式，编制简单易行的Matlab 程序，从而可迅速得到板结构内的弯矩分布，为结构工程师设计此类板结构提供参考。

1 任意曲线线荷载作用下单向板的弯矩计算公式

如图1所示的四边简支矩形板，当长边b比短边a大三倍时，可认为矩形板为单向板。板上受到任意的曲线线荷载q（q=常数）如图1所示，曲线形状由函数y=f（x）确定。坐标系建立如图1所示。

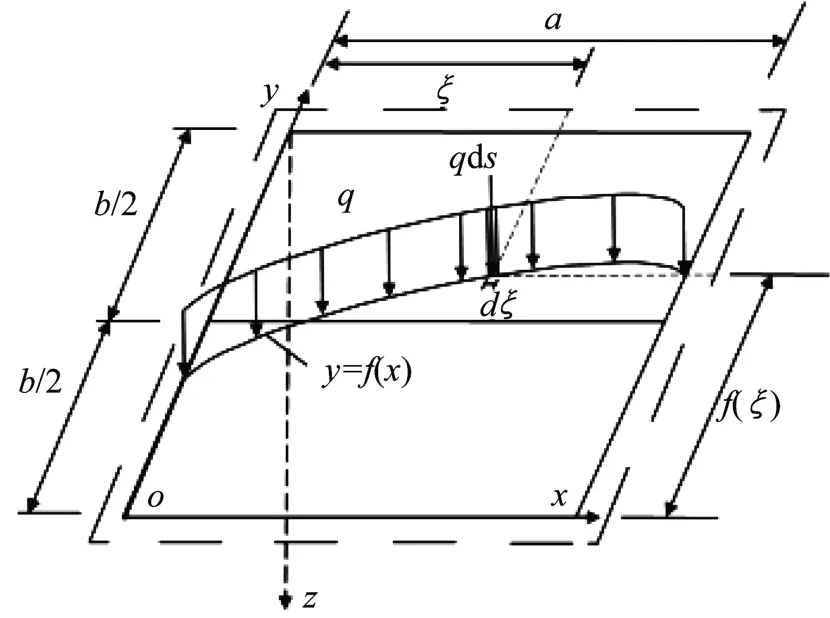
图1 四边简支矩形板承受任意线荷载作用Fig.1 Four-side simply-supported slab under arbitrary line load

根据薄板理论［3，7］，当简支矩形薄板上任意位置（x0，y0）作用有集中荷载P时，板内任一点（x，y）的弯矩为

对于任意曲线线荷载q而言，作用在曲线任意位置［ξ，f（ξ）］上微段 ds的集中荷载为 dP=dξ（见图1），根据式（1），该集中荷载产生的弯矩如式（2）所示。

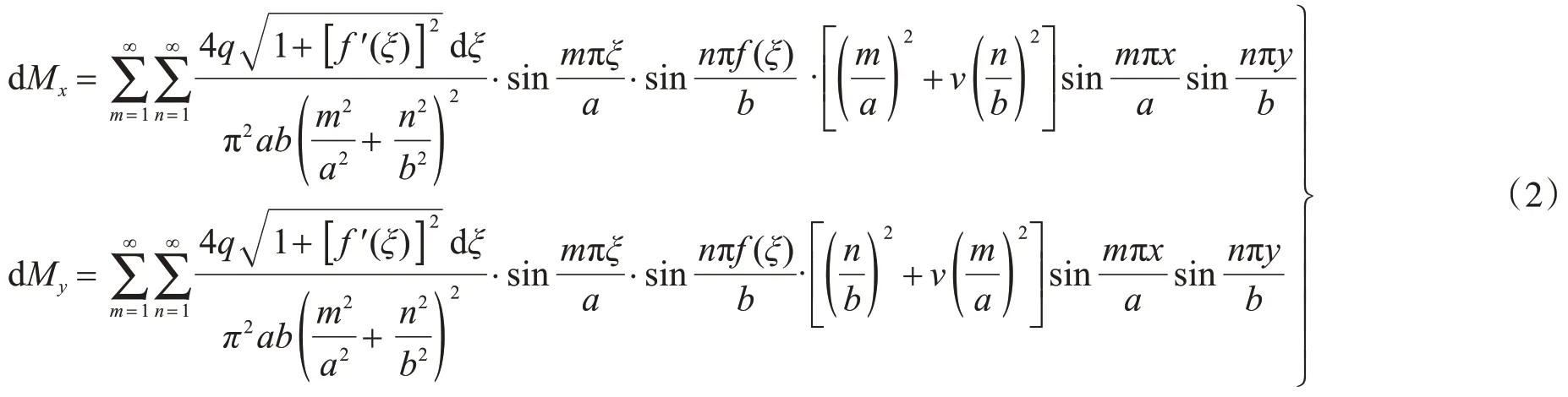
于是整条线荷载q在任意一点（x，y）所产生的弯矩，通过积分式（2）可得式（3）。

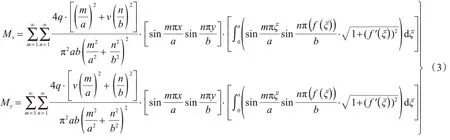
式中：ξ为选取的微元荷载在x方向上的坐标；ν为单向板材料的泊松比，对于混凝土材料而言，ν=1/6；f′（x）为线荷载函数曲线y=f（x）的导数。

对于一般的曲线函数而言，式（3）的积分式难以得到解析解答，可通过数值积分得到解答。本文编制了数值计算MATLAB程序列于附录。

2 算例分析

2.1 曲线线荷载作用下单向板的弯矩计算

单向板弯矩算例：某混凝土单向板，矩形板长边b=12 m，短边a=3.6 m，厚度t=0.2 m，密度ρ=2 400 kg/m3，泊松比ν=1/6。板上作用有曲线荷载q=80 kN/m，曲线荷载函数为

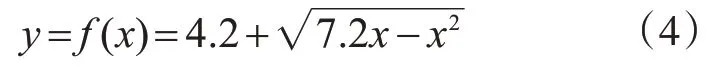
板内弯矩可以分别采用MATLAB 程序及ANSYS软件计算。

将以上数据及曲线函数代入式（3）积分，根据附录MATLAB 程序，计算得到板内的弯矩分布如图2 所示。曲线线荷载所产生的弯矩最大值均出现在线荷载作用的中心位置。主方向弯矩最大值（Mx，max）=38.40 kN·m，次方向弯矩最大值（My，max）=26.70 kN·m。

图2 弧线荷载作用下主次方向弯矩分布（MATLAB）Fig.2 Moment distributions in primary and secondary directions under arc load（MATLAB）

在ANSYS 软件中，根据以上数据建立相同的计算模型，弯矩计算结果如图3 所示，主次方向弯矩最大值分别为38.70 kN·m，25.83 kN·m。根据图2、图3 结果，可以发现本文MATLAB 程序计算结果与ANSYS 结果很吻合，表明本文MATLAB 计算方法和程序可靠，对于曲线线荷载作用下的弯矩计算结果足够精确。

2.2 单向板次方向配筋分析

在单向板设计中，结构工程师一般主要关注短跨（主方向）上的配筋计算，通常按计算最大弯矩（Mx，max）进行配筋计算，然后根据计算的配筋在全跨布置受力钢筋。本文对于主跨方向的配筋设计不再赘述。

实际工程中，结构工程师容易忽视长跨（次方向）的弯矩分布与配筋计算，长跨方向常常可能采用构造配筋。由图2、图3 可以看出，主次方向最大弯矩位置接近，大小也接近，所以根据设计规范［8］，在次方向按构造布置的分布钢筋一般难以满足最大弯矩的承载力要求，会导致荷载裂缝，危及结构安全。因此考虑在单向板次方向最大弯矩处布置一定长度的附加短钢筋，保证次方向满足板的抗弯承载力要求。为了更直观地观察到次方向附加钢筋的配筋要求，截取曲线荷载作用下单向板最大弯矩附近的几个剖面进行弯矩分布计算，由此进行配筋分析，剖面位置分别为：x=1.2 m（1-1 剖面）、x=1.4 m（2-2 剖面）、x=1.6 m（3-3 剖面）、x=1.8 m（4-4 剖面）、x=2.0 m（5-5 剖面），如图4所示。

图3 弧线荷载作用下主次方向弯矩分布图（ANSYS）Fig.3 Moment distributions in primary and secondary directions under arc load（ANSYS）

图4 剖面位置Fig.4 Section position

各个剖面上的弯矩分布如图5 所示，对于短跨的抗弯钢筋，可以根据主方向最大弯矩Mx，max的配筋进行通长配置。对于次方向的弯矩，由图5可以看出，在主方向最大弯矩处，次方向的弯矩远超出了分布钢筋的抗弯能力（实际工程中分布钢筋的配筋量一般要求取主方向钢筋15%左右［8］），需要额外配置附加钢筋，附加钢筋配置如图6所示。

由于构造钢筋的配筋量一般取主方向钢筋的15%左右，所以为了不造成浪费，附加钢筋只需要配置在次方向弯矩大于15%Mx，max的部分就足以满足承载力要求了，如图6 所示，其中20d为钢筋在影响范围以外增加的锚固长度［8］。

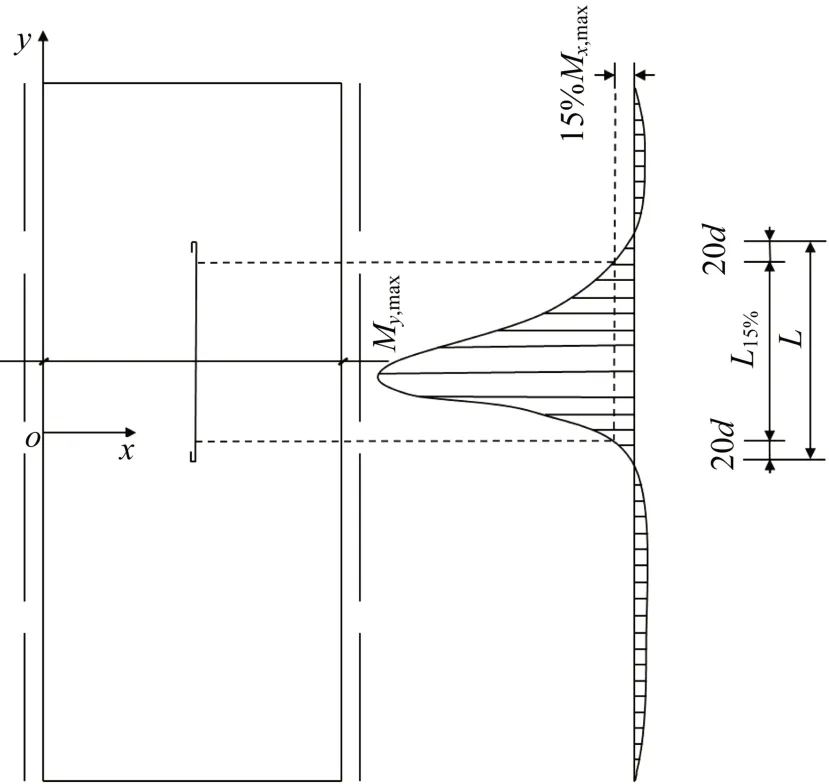
图6 单向板附加钢筋配筋简图Fig.6 Reinforcement diagram of one-way plate with additional reinforcement

本文仅给出了板内主次弯矩的计算大小和分布情况，具体配筋量计算可参照《混凝土设计规范》（GB 50010—2010）［8］执行，相应的构造要求可参照规范及以上本文的要求办理。

3 结 语

本文给出的任意曲线荷载下板内弯矩计算公式具有很好的计算精度，给出的Mablab 计算程序可为结构工程师处理此类复杂曲线荷载问题的配筋计算提供参考。附录中的MATLAB 程序在针对实际问题时，只需要修改单向板尺寸（a，b），曲线荷载线荷载大小以及函数形式（q，load），就可以得到需要的弯矩分布。