基于局部变形假定的锚固类结构锚固段剪应力分布研究

2021-10-22范俊奇孔福利石晓燕贺永胜

结构工程师 2021年4期

范俊奇孔福利石晓燕贺永胜

（军事科学院国防工程研究院，洛阳471023）

0 引言

锚固类结构是指基于锚固技术的锚杆、锚索和土钉一类岩土工程加固、支护结构。为方便起见，本文将锚杆（索、钉）体表面与注浆体之间的界面称为“第一界面”，将注浆体与孔壁之间的界面称为“第二界面”［1，4，7-8］。对于锚杆为代表的锚固结构，其第一、第二界面上的剪应力是工程设计的基本依据和前提。但时至今日，我国有关锚固类结构技术规范，采用的仍然是平均剪应力的概念和方法，这与锚固技术的发展是不相适应的。国内外大量的研究表明［1-16］，剪应力在锚固段并非是均匀分布，而是呈现出单峰或者指数函数的分布形式，但对于锚固段剪应力的具体分布形式，目前仍存在着不同的观点。文献［7］通过模拟高、中、低三种强度的围岩介质锚杆模型拉拔试验，对锚杆锚固段的轴应变及锚固段剪应力分布规律进行了研究，认为剪应力在孔口处为零，在接近孔口处达到最大值，然后以负指数规律沿锚杆方向衰减。文献［8］在Mindlin 位移解的基础上，对全长粘结锚杆锚固段受力进行了理论研究，结果表明锚固段剪应力在起点处最大，向后逐渐衰减并最终趋近于零；张季如等［9］建立了锚杆荷载传递的双曲函数模型，蒋忠信［10］提出了用三参数的高斯曲线来描述锚固段剪应力分布曲线；同时大量现场试验研究表明［11-12］，剪应力峰值并非出现在锚固段的起点，而是出现在锚固段中的某一处。

综上所述，虽然国内外关于锚固类结构锚固段剪应力的测量及试验研究成果较为丰富，但这些研究大多是单独进行的，缺乏系统性，存在理论分析假设与试验和工程实际不相符的情况，因此，有必要对锚固段剪应力的分布规律做进一步分析，以便寻求更加符合实际的结论。本文基于全长注浆锚杆的拉拔试验，在“局部变形假定”的基础上，对不同介质类型中的全长注浆锚杆内锚固段的轴力及界面剪应力分布规律进行了较深入的研究，推导了稳定介质内锚固段应力、轴力及交界面剪应力分布的理论公式，并将其与试验结果进行了对比，结果表明，理论解与试验结果基本吻合。本文分析了以锚杆为代表的锚固类结构第一、第二界面剪应力分布，对工程实践具有指导参考价值。

1 锚固段受力分布分析

1.1 基于“局部变形假定”计算锚固段应力分布理论解

“局部变形假定”用一系列独立作用的“切向弹簧”来描述“锚固体”（指锚杆或锚杆与注浆体的“复合体”）同围岩之间的相互关系［13］，并假定注浆体处于弹性状态。对于压力型锚杆，由于锚杆体与注浆体之间没有粘结作用，可以认为锚索荷载是通过端部的承压板转化为压缩力而全部作用在注浆体上，依据局部变形假定，可以将注浆体与周围介质之间的相互关系简化为一系列独立作用的切向弹簧。若设锚杆锚固段长度为L，在距离锚固端口部（拉力型锚杆）或尾部承压板（压力型锚杆）为x的注浆体上取出一微段dx，其受力示意图如图1 所示，则该微段上的剪应力（即粘结应力）可由下式计算得到［4，13］：

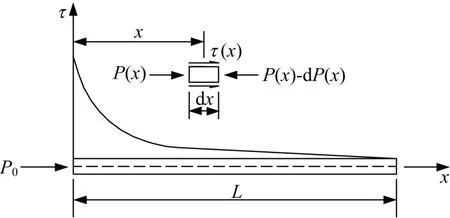
图1 锚固段受力分析示意图Fig.1 Mechanical schematic of the internal anchorage section

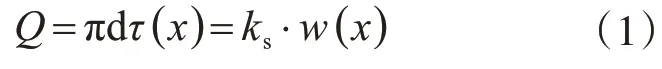
式中：τ（x）为x处锚杆体或注浆体周边粘结应力（kPa）；W（x）为x处注浆体与孔壁或注浆体与杆体间的相对位移（mm）；ks为综合切向刚度系数，文献［13］中称之为岩土层的反力系数（MPa）。

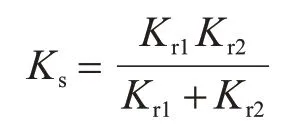
式中：Kr1为注浆体的剪切刚度；Kr2为围岩体（介质）的剪切刚度。

图1 中，注浆体口部（拉力型）或底端（压力型）（x＝0 处）受到一拉力（拉力型锚杆）或压力（压力型锚杆）P0的作用，在沿注浆体轴线方向并距离底端x处的一微段dx上，其周边的粘结应力为 τ（x），两侧所受的轴力分别为P（x）和P（x）-dP（x）。

由dx微段的轴向平衡条件∑x=0，可得微段上的轴力 dP（x）与剪应力 τ（x）之间存在如下关系：

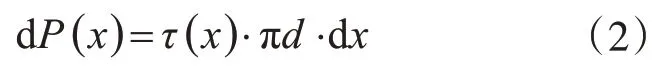
式中，d为杆体的直径，对压力型锚杆，d应为注浆体直径D。

在x处杆体（注浆体）的应变ε（x）与其相对位移w（x）及轴力存在如下关系：

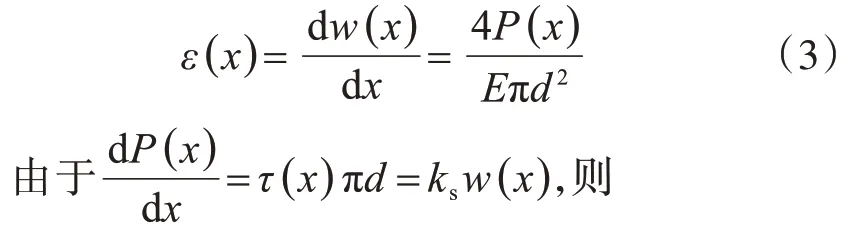
代入边界条件：当x＝0时，P（x）=P0；x＝l时，P（x）=0。则有

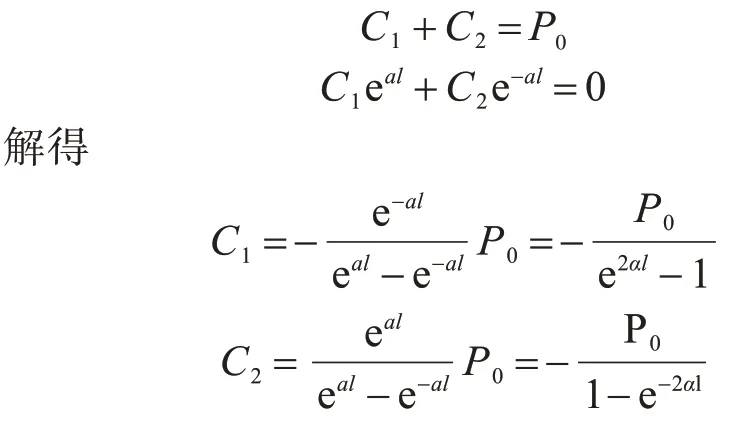
代入式（5）可得出轴力的计算公式：

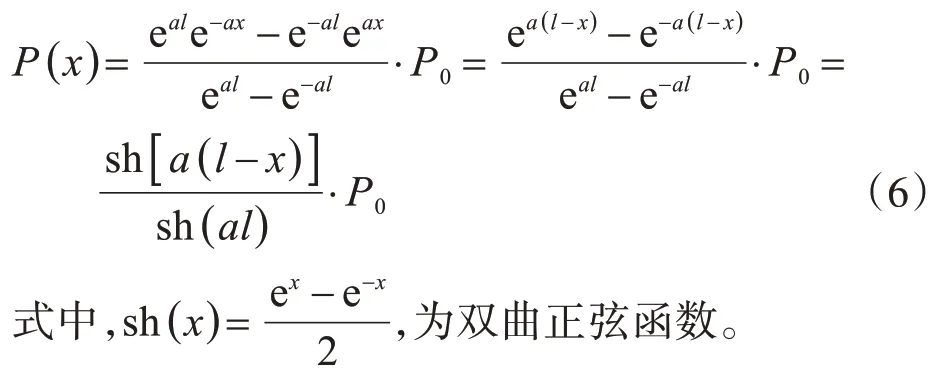
将式（6）的结果代入式（2）可以得：

同样，根据式（3）可得：

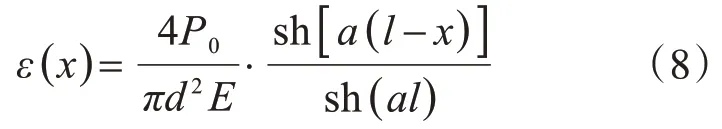
在式（6）和式（7）中，关键是综合切向刚度系数ks的确定。综合切向刚度系数ks其实应该包括两部分，即由注浆体变形引起的组分kbond和由岩土体变形引起的组分kr：

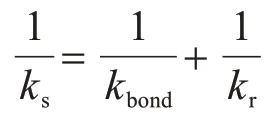
kbond可根据弹性力学中的厚壁圆筒解求得：

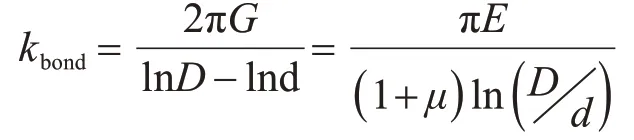
式中：G、E和μ分别为注浆体的剪切模量、弹性模量和泊松比；d和D分别为锚杆（钢筋）和注浆体的直径。

对于岩石中锚杆，由于岩石的弹性模量远大于注浆体的弹性模量，可忽略岩体的变形，将岩体视为绝对刚体，即ks＝kbond。同样，而对于土中锚索，注浆体的弹性模量远大于土体，可忽略杆体的变形，将杆体和注浆体组成的复合体作为锚固体，切向刚度系数主要由土体的变形特性确定，即ks＝kr。表1为文献［13］建议的各类不同岩土体的综合切向刚度kr的经验值。

1.2 第一、第二界面剪应力公式的推导

由以上推导可知，依据局部变形假定推导的剪应力计算公式只有一个。要使其结果能同时计算第一界面和第二界面的剪应力，需对公式的适用性进行拓展分析讨论。由式（7）的具体形式可知，计算界面的剪应力时，关键在系数ks和a的确定，其中综合切向刚度系数ks可参照表1 进行取值，其他参数取值如下：

表1 文献［13］建议的各类岩土的切向刚度Table 1 The suggested shearing rigidity from document［13］

锚杆体：直径d=0.018 m；弹性模量E=2.1×105MPa。

注浆体：直径d=0.047 m；弹性模量E1=1.5×103MPa；泊松比μ1＝0.3。

高强介质：弹性模量E2=2.8×103MPa；泊松比μ2＝0.3。

中强介质：弹性模量E1=1.5×103MPa；泊松比μ1＝0.3。

低强介质：弹性模量E3=5.0×102MPa，泊松比按坚硬的黏性土取值μ3＝0.25。

因此各介质的切向刚度计算结果如下：高强介质，kr=5 287.5 MPa；中强介质，kr=3 776.8 MPa；低强介质，kr=1 309.3 MPa。

计算中，第一、第二交界面的系数a分别记作a1、a2。在计算a1时，公式中的参数d、E分别取锚杆体的直径和弹性模量；在计算a2时，公式中的参数d、E分别取注浆体的直径D和锚杆与注浆体的“复合体”弹性模量Es，其算式为［13］

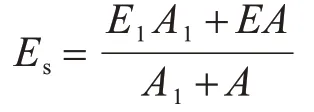
式中：E为锚杆体的弹性模量；E1为注浆体的弹性模量；A为钢筋的截面积；A1为注浆体承压面积。

则对式（7）中的综合切向刚度系数ks及系数a的值可分别计算如下：

由于本文讨论的锚杆是作用力接近使锚杆屈服时，即杆体上应变接近为0 的锚杆长度，一般情况下，应有l≥50 mm。则式（6）中：

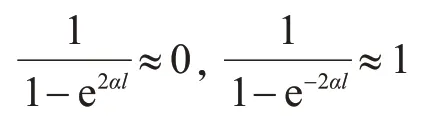
此时，式（6）-式（8）可分别简化为

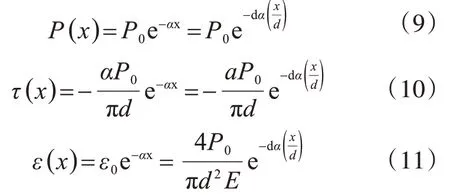
将计算出的a值分别代入式（9）-式（11）中，即可求出各类锚杆在不同的荷载下轴应变与界面剪应力值分布，计算中各参数取值如下：在计算杆体轴应变以及第一交界面的剪应力时，式中d取锚杆体的直径d=0.018 m；在计算第二交界面的剪应力时，式中d取注浆体的直径D=0.047 m。图2为依据上述公式分别计算所得的中强介质锚杆杆体轴应变与第一、第二交界面的剪应力分布。

从图2 可知，锚杆轴应变及第一、第二交界面的剪应力分布的共同特征为：

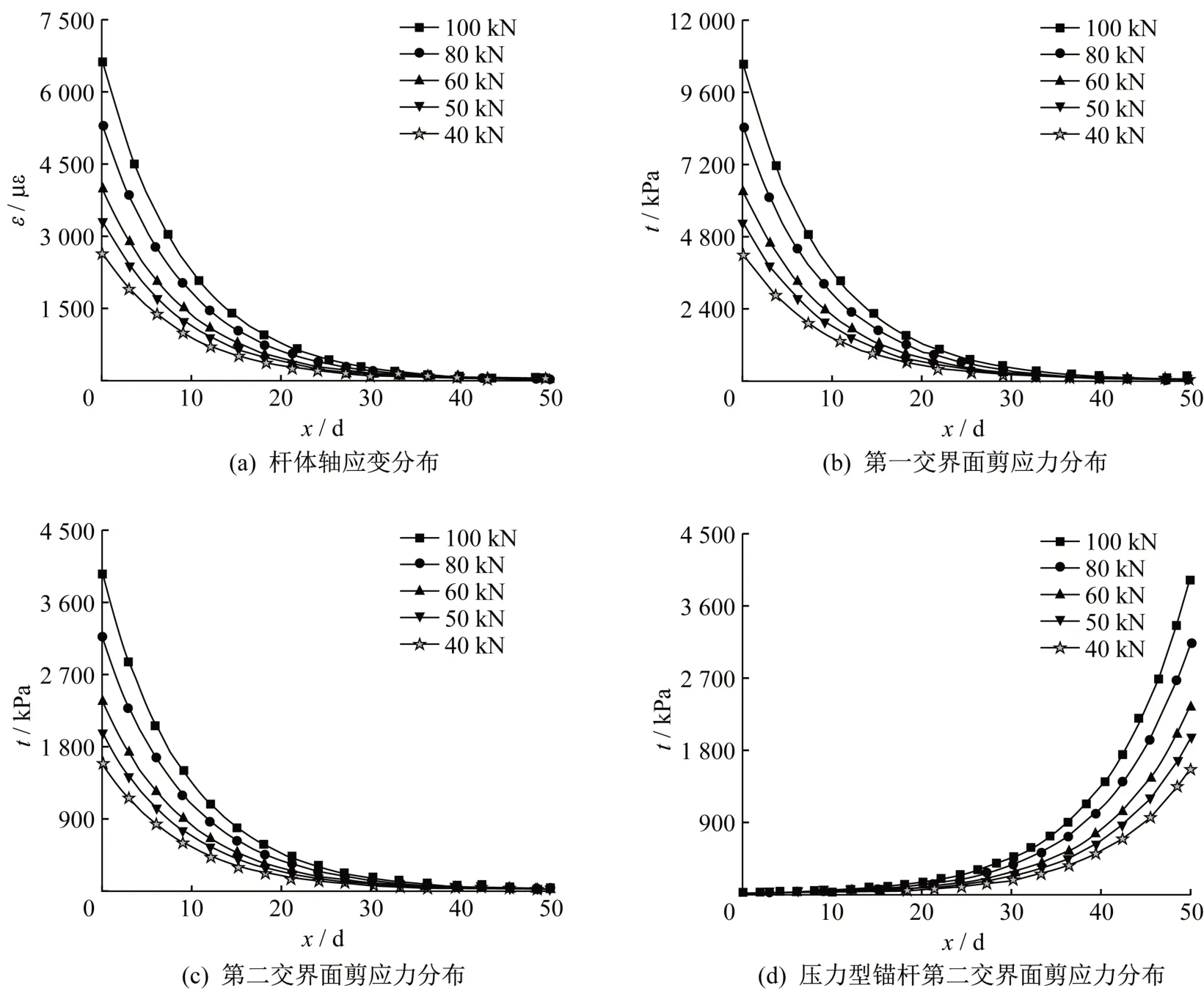
图2 锚杆杆体轴应变及剪应力分布图Fig.2 The strain&shear stress distribution under different stretching forces

（1）在杆端处（x/d=0），应变、轴力为最大值，其后沿轴线方向按负指数规律迅速衰减。

（2）锚杆第一、第二交界面的剪应力分布规律是相同的，只是剪应力集度不同（计算结果相差约2.5 倍）。剪应力在孔口处最大，然后以较快的速率按负指数规律沿锚杆方向衰减。

（3）由于轴力和剪应力衰减很快，因此锚杆轴力和有效剪应力值仅分布在杆体的有限长度范围内（约40d），锚杆的主要承力部位在其内锚固段的前部大约40倍锚杆直径，即在距离口部700 mm左右。

（4）锚固段剪应力具有同步转移特性，随着拉拔荷载增大，其零值剪应力向杆体深部的转移，即剪应力影响逐渐增大，这是由于砂浆体局部产生破损的结果。

2 不同类型介质中锚固类结构锚固段剪应力的分布分析

锚杆锚固段的剪应力分布区域直接决定着锚杆的有效锚固长度，从式（10）、式（11）可知，锚固段剪应力的大小及分布受介质性质的影响，图3分别列出了高强岩体介质、风化岩体介质和土体介质三种不同强度介质类型中锚杆锚固段剪应力分布计算结果对比。

从图3 可知，对于不同介质类型中的锚杆，其剪应力分布形态是相同的，只是其衰减速率和受力区域不同，高强岩体介质中锚杆的受力区域为距孔口深度约30d的长度区域上；中强风化岩体介质中锚杆的受力区域为距孔口深度约40d的长度区域上；低强土体介质中锚杆的受力区域为距孔口深度约50d的长度区域上。由此可以得出：介质强度越高锚杆所受的剪应力、轴力越大，剪应力轴力的分布范围越小，越集中，锚杆的有效锚固长度也就越小；介质强度越低，锚杆所受的剪应力、轴力越小，剪应力轴力的分布范围越大、越均匀，锚杆的有效锚固长度也就越大。因此从某种意义上说，用全场粘结锚杆加固软岩和土体的效果比加固硬岩更好。

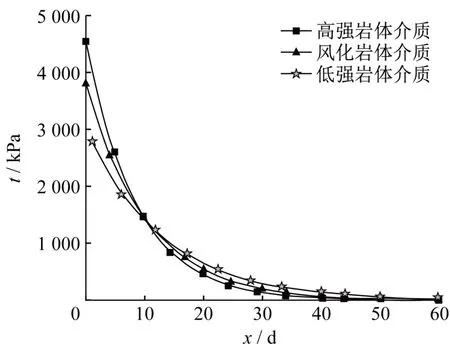
图3 不同介质中锚杆剪应力分布Fig.3 Variations of shear stress distribution of bolt in deference medium

3 理论分析解与试验结果对比分析

为验证理论结果的可靠性，特将理论结果与文献［7］的试验结果进行对比，文献［7］的试验中，用φ18 mm 的螺纹钢筋制作锚杆，注浆体为水泥砂浆，其直径为47 mm，28天强度为32.2 MPa；高、中、低三种强度围岩介质分别用28 天强度为53.2 MPa、32.2 MPa、7.2 MPa的水泥砂浆和水泥拌合土来模拟，通过WES-50B 型万能材料试验机对其进行拉拔试验。图4 为本文推导所得的当杆端拉力为40 kN 时中强介质中锚杆体轴应变和剪应力分布结果与文献［7］中相同条件下的试验结果在同一坐标系的对比。

通过图4 的对比可知，本文推导的理论解与试验所得的杆体轴应变的分布形态吻合较好，即杆体轴应变在孔口最大，之后随距孔口距离的增大按负指数规律迅速衰减，并很快趋于零，只是应变的衰减速率不同。本文依据“局部变形假定”所推导的计算结果在锚固段前半部衰减较块，在后半部衰减较慢，轴应变分布区域较大。

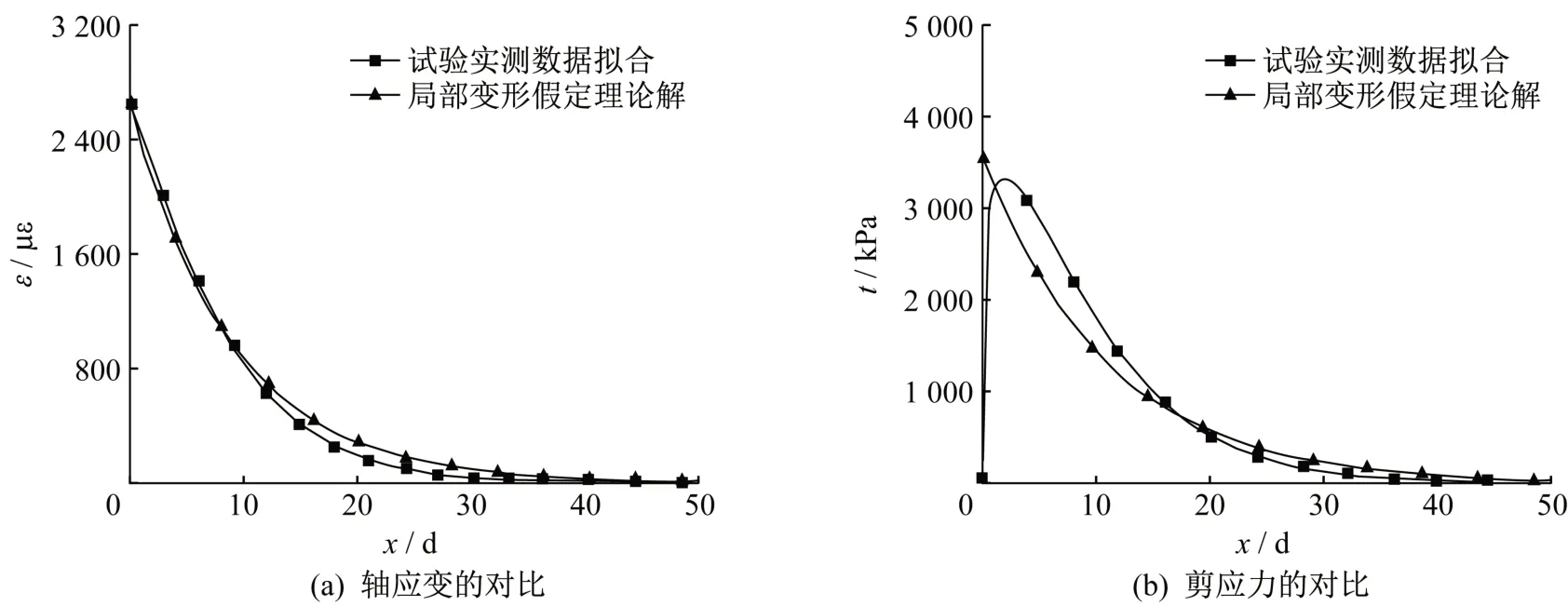
图4 理论解与根据试验推导结果对比Fig.4 Comparisons between results of analytic solution and the experiment

理论解和试验所得锚杆锚固段剪应力分布形态也基本相同，仅在口部部位略有差异，即峰值剪应力出现位置略有差别，根据“局部变形假定”所计算的峰值剪应力位于孔口受力点（x/d=0）处，之后以较快的速率按负指数规律沿锚杆方向衰减。而依据试验所得剪应力在孔口处（x/d=0）为零，在非常接近孔口处达到最大值，然后以较快的速率按负指数规律沿锚杆方向衰减。不同的是，两种结果所得的剪应力峰值出现的位置不同，而其大小约为3 500 kPa，分布区域较大（约为40d）；而依据试验所的结果在受力点处剪应力为零，峰值剪应力位于非常接近于受力点位置（在受力点后约2d处），大小为3 400 kPa，分布区域相对较小（约为35d）。

通过以上对比分析可知，本文基于“局部变形假定”得到的锚杆体轴应变分布的结果与依据试验测试所得结果基本吻合；所得到的杆体轴应变及剪应力的分布形态与试验拟合结果较类似。仅在峰值剪应力大小、出现位置和分布区域上略有差异，从结果来看基于“局部变形假定”所得结果略偏向于保守，但这对实际工程来说无疑是有利的。