钢筋混凝土弯曲破坏试验柱的截面尺寸效应研究

张国军 梁本亮

（上海师范大学建筑工程学院，上海201418）

0 引 言

随着社会、经济和科技的迅猛发展，在高层或超高层结构、大跨结构、预应力结构以及其他大型重型工业建筑结构中，跨度和高度不断增加，结构构件尺寸愈来愈大，显示出更为突出的钢筋混凝土柱破坏尺寸效应问题。对这类问题，结合国内外相关规范［1-2］国内外研究者开展了一些的试验和数值研究［3-16］。Sener S、Majewski T 和杜修力等［4-13］主要分析了混凝土强度等级、长细比以及加载方式等对钢筋混凝土柱截面尺寸效应的影响规律。主要研究结论有：长细比愈大，钢筋混凝土柱的尺寸效应愈明显［8］；柱子长细比愈大，柱破坏愈脆［9］；混凝土强度愈高，柱破坏愈脆［10］；配箍率愈大，尺寸效应被减弱，尺寸效应愈不明显［11］；随轴压比增大，柱的名义极限受弯承载力增大，但其变形能力明显降小，尺寸效应愈显著；在受压或者受剪作用下，钢筋混凝土短柱呈脆性破坏模式，名义抗剪强度有明显的尺寸效应［11］。钢筋混凝土柱尺寸效应的研究呈现的主要特点是：轴心加载研究偏多，偏心加载研究偏少；单调加载偏多，循环往复加载偏少；定性分析的较多，定量分析的较少。本文根据收集的钢筋混凝土试验在柱固定轴向荷载水平低周反复荷载作用下的试验结果，定量分析和探讨了截面尺寸对钢筋混凝土弯曲破坏试验柱的受弯承载力、屈服、峰值和极限水平承载力、延性、极限位移角、各刚度及塑性转动能力的变化规律，然后在理论分析和试验结果分析的基础上，推出了考虑截面尺寸效应的钢筋混凝土柱正截面大偏心受压破坏的受弯承载力计算公式，为钢筋混凝土结构尺寸效应研究提供了一定的依据。

1 试验柱试验数据的收集

本文搜集整理了国内外近年来诸多学者［17］以及笔者［18-20］做过的共 218 根剪跨比大于 2 仅发生弯曲破坏的钢筋混凝土试验柱在恒定竖向荷载和水平低周往复荷载作用下的试验结果。不包括短柱，有两种箍筋形式：普通箍和复合箍，全部试验柱均有滞回曲线，两端固定或两端铰接形式加载柱已转化为悬臂柱，很多学者提供的试验数据考虑了P-Δ效应［17］。对框架柱试验研究时，轴压比通常有标准轴压比nk和设计轴压比n，它们之间的关系n/nk=1.68，具体推导见文献［18］，其中，试验柱的其他基本参数依据文献［18］来确定，试验柱参数特性范围值详见表1。

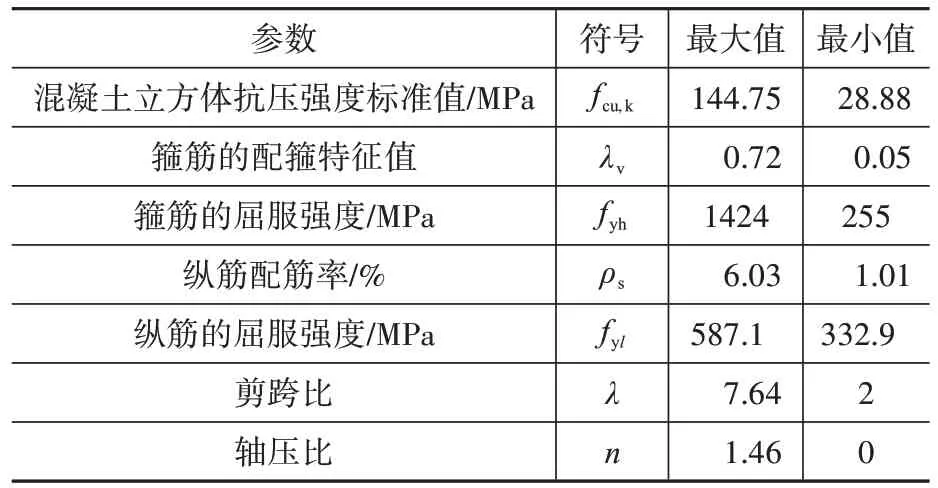
表1 收集试验柱的参数特性范围Table 1 Range of properties in collected column database

2 试验柱的结果分析

根据收集的试验结果，首先用软件MATLAB编制计算程序［20］，然后用编制的程序计算出试验柱的骨架曲线、屈服荷载和屈服位移、最大荷载和最大位移、极限荷载和极限位移、延性、弹性刚度、强化刚度、最大刚度和退化刚度，最后根据Origin软件的回归结果分析了截面尺寸对试验柱的承载力、延性、刚度及塑性转动能力的影响规律。

2.1 截面尺寸对柱承载力的影响规律

由于绝大部分试件截面为方形截面柱，所以以横截面高度的变化来分析试验柱受剪和受弯承载力的影响规律。图1 给出了名义屈服剪力Vy/(fcbh0)随截面高度h的变化规律，其中Vy为试验柱承受的水平屈服剪力，从图1 可以发现，当轴压比在0.7～1.0 时，截面高度h愈大，名义屈服剪力愈小，当轴压比小于0.7 及轴压比大于1.0时，截面高度h愈大，名义屈服剪力愈大。

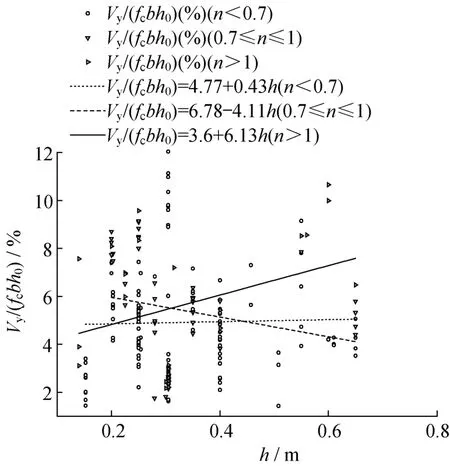
图1 名义屈服剪力与截面高度间的关系Fig.1 The relationship between nominal yield shear force and cross section height

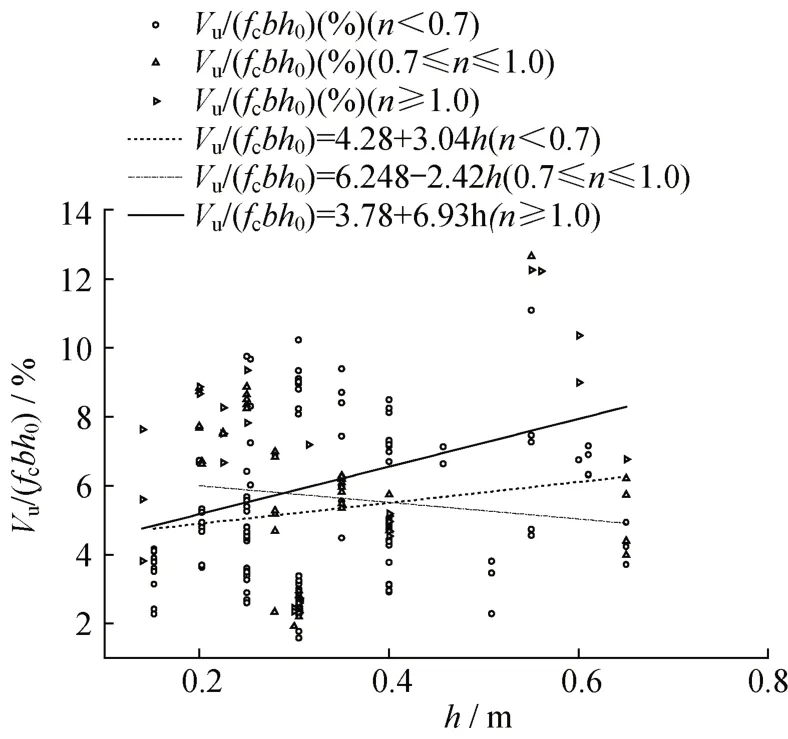
图2 名义极限剪力与截面高度间的关系Fig.2 The relationship between nominal ultimate shear force and cross-sectional height

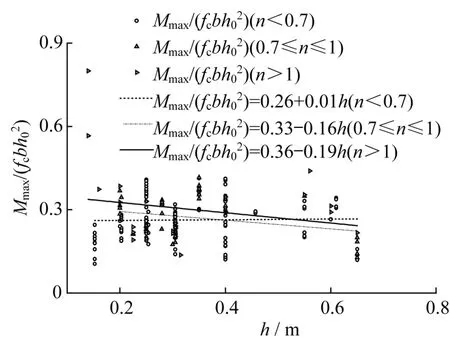
图3 名义弯矩与截面高度间的关系Fig.3 The relationship between nominal bending moment and cross-sectional height

从以上分析可知，轴压比在中高值（0.7～1.0）时，试验柱的名义屈服剪力和名义极限剪力存在截面尺寸效应。轴压比大于0.7时，试验柱的名义弯矩存在截面尺寸效应。

2.2 截面尺寸对柱延性的变化规律

图4 和图5 给出了试验柱的延性随截面面积和截面高度的变化规律，从图4 和图5 可以发现，当轴压比在0.7～1.0时，随着截面面积或者截面高度的增加，试验柱的延性逐步降低；当轴压比在0～0.7 及轴压比大于0.7 时，随着截面面积或者截面高度的增加，试验柱的延性逐步增大。经过对试验结果进行线性回归，当轴压比在0～0.7 时，得出延性系数μ1与截面面积A和截面高度h之间的关系式为

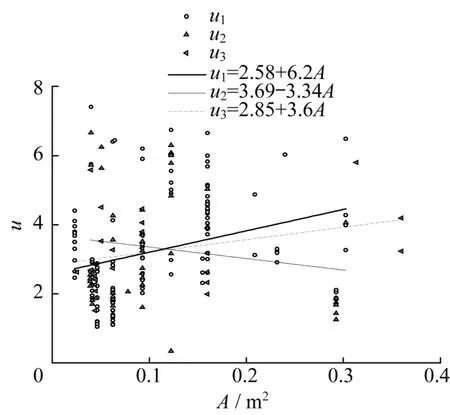
图4 延性与截面面积间的关系Fig.4 The relationship between ductility and cross-sectional area

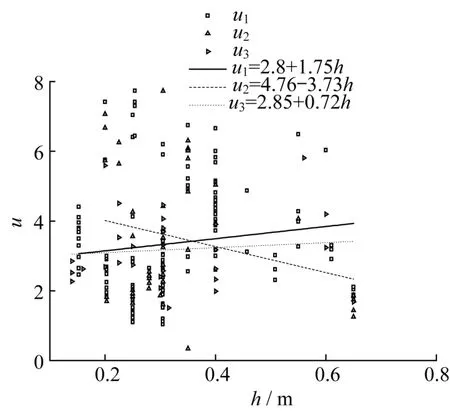
图5 延性与截面高度之间关系Fig.5 The relation between ductility and cross section height

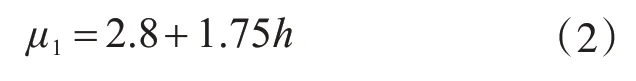
当轴压比在0.7～1.0时，得出延性系数μ2与截面面积A和截面高度h之间的关系式为

当轴压比在大于1.0 时，得出延性系数μ3与截面面积A和截面高度h之间的关系式为

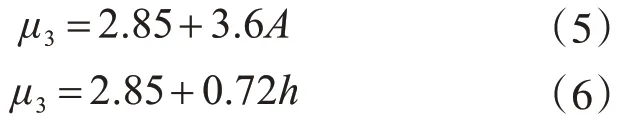
总而言之，当轴压比在0.7～1.0 时，截面尺寸效应对试验柱延性有降低的影响。

2.3 截面尺寸对柱刚度的影响规律

试验柱的弹性刚度、强化刚度和退化刚度可表示为［9］

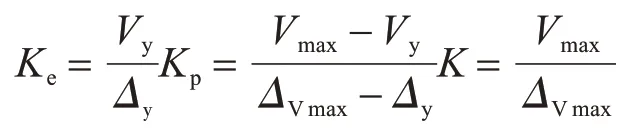
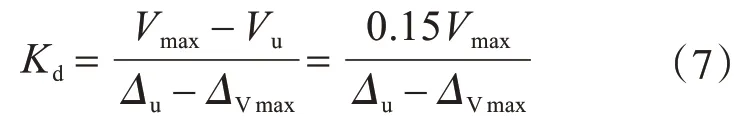
式中：Ke、Kp及Kd分别为试验柱的弹性刚度、强化刚度及退化刚度；K为试验柱的最大水平荷载Vmax与最大水平荷载时的柱顶水平位移ΔVmax的比值，称为最大刚度。

由钢筋混凝土弯曲破坏试验柱的试验结果分析得出，试验柱的强化刚度Kp、退化刚度Kd及最大刚度K与截面尺寸均具有一定关系，它们与弹性刚度Ke比值随截面高度的影响规律见图6-图8。从图6 中可以得知，随截面高度的增大，当轴压比小于或等于1 时，试验柱的强化刚度Kp与弹性刚度Ke的比值增大，而当轴压比大于1时，试验柱的最大刚度K与弹性刚度Ke的比值减小。从图7 中可以得知，随截面高度的增大，试验柱的退化刚度Kd与弹性刚度Ke的比值增大。从图8 可以得知，随截面高度的增大，当轴压比在0.7～1.0时，试验柱的最大刚度K与弹性刚度Ke的比值增大；当轴压比小于0.7或大于1.0时，试验柱的最大刚度K与弹性刚度Ke的比值减小。

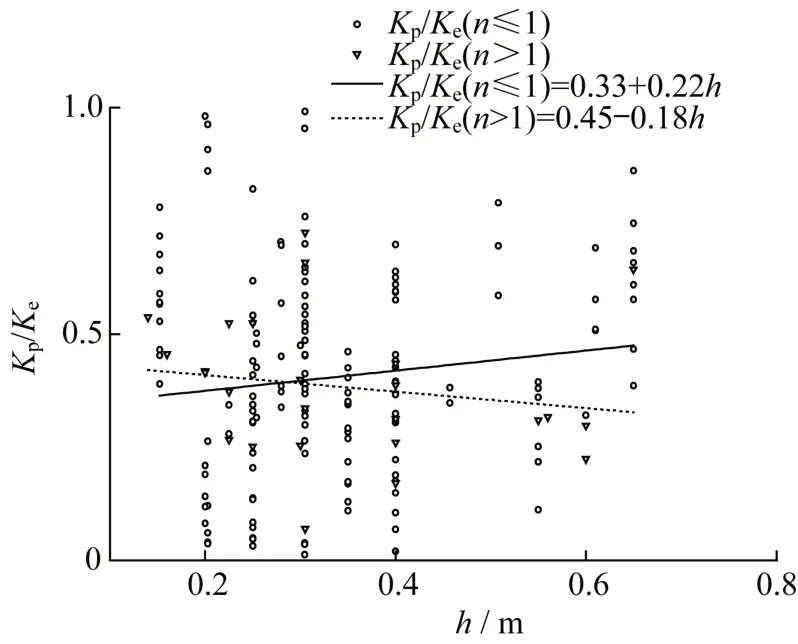
图6 强化刚度与弹性刚度的比值与截面高度间的关系Fig.6 The relationship between the ratio of strengthened stiffness to elastic stiffness and cross section height

图8 最大刚度与弹性刚度的比值与截面高度间的关系Fig.8 The relationship between the ratio of maximum stiffness to elastic stiffness and cross section height

简而言之，当轴压比大于1 时，截面尺寸效应对试验柱最大刚度与弹性刚度比值和试验柱强化刚度与弹性刚度比值有降低的影响。

2.4 塑性铰转动能力

塑性铰的转动能力一般用试验柱极限位移时相对转角和屈服时相对转角之差来表示。又由于本次收集的柱试验数据均为发生弯曲破坏的长柱，主要以弯曲变形为主，因此试验柱的塑性铰转角θp［13］以式（8）近似表示。

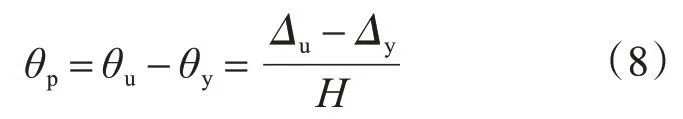
图9给出了试验柱的塑性转角θp随截面高度的变化规律，从图9 可以发现，随着截面高度的增大，当轴压比小于0.7 时，试验柱的塑性铰转角θp增大，而轴压比大于或等于0.7 时，试验柱的塑性铰转角θp减小，且随着轴压比增大，试验柱的塑性铰转角θp减小的幅度越来越小。故只有当轴压比大于0.7时，截面尺寸效应对试验柱塑性铰转角有降低现象。

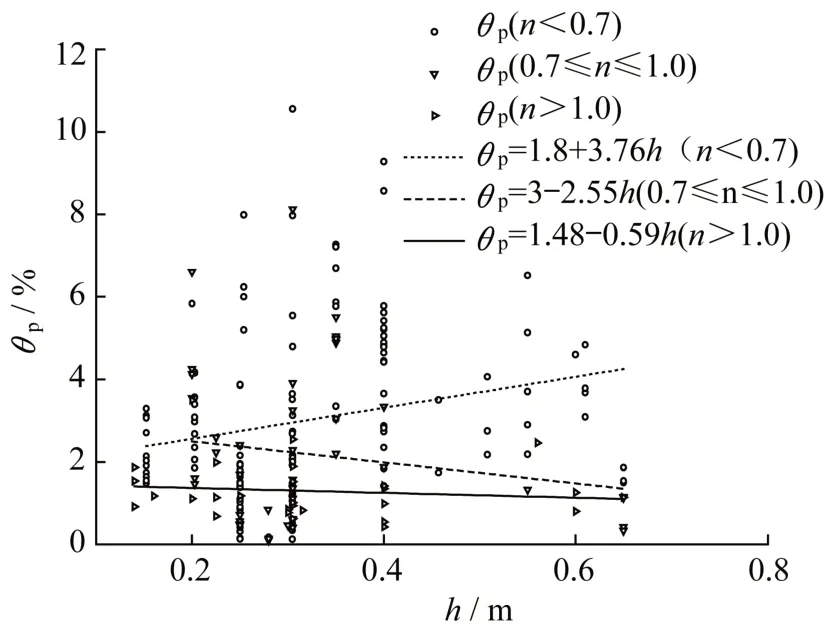
图9 塑性铰转动能力与截面高度间的关系Fig.9 The relationship between the rotational capacity of plastic hinge and cross section height

3 柱受弯承载力的截面尺寸效应

3.1 柱受弯承载力的计算

由于试验柱均为在固定轴向荷载和水平周期反复荷载作用下的对称配筋矩形截面的试验结果，所以试验柱的受压承载力Nu为已知，下面根据《混凝土结构设计规范》（GB 50010—2010）［1］推出柱抗弯承载力Mu的计算公式。《混凝土结构设计规范》（GB 50010—2010）中的正截面受弯承载力计算公式为

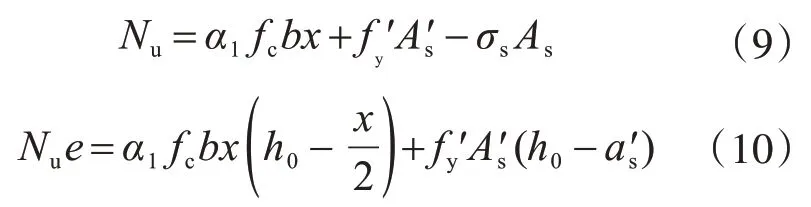
若为大偏心受压构件，式（9）、式（10）变转正为

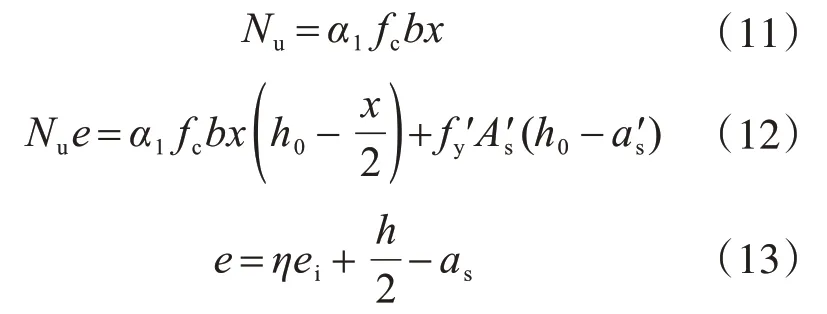
由式（11）、式（12）及式（13）可推出柱的抗弯承载力Mu为

若为小偏心受压构件，式（9）、式（10）转正为

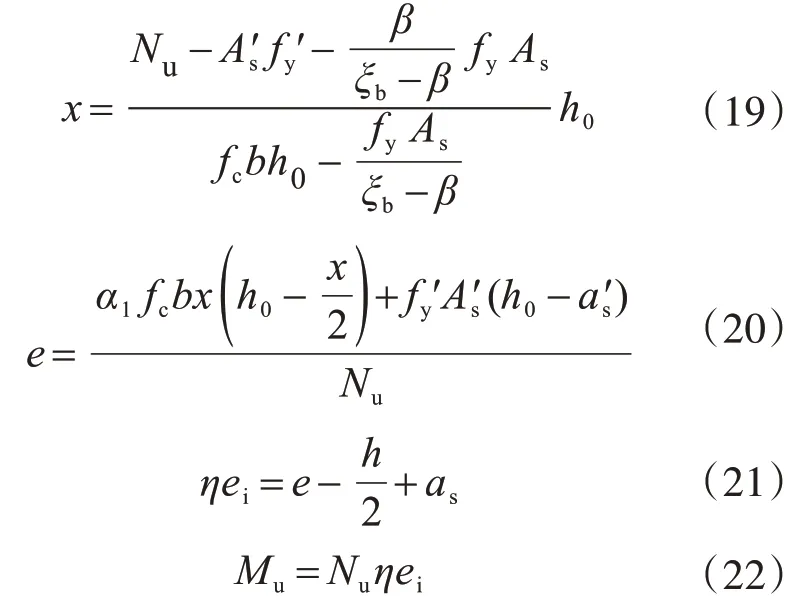
3.2 试验结果与规范公式的比较

根据全部试验柱试验与计算结果的回归分析，图10 给出了试验柱的安全储备系数K与截面高度h的变化规律。从图10 可知，随着截面高度的增大，当轴压比在0.7～1.0 时，试件的安全储备系数K减小，表现出明显的尺寸效应，当轴压比小于0.7或大于1.0时，试件的安全储备系数K增大。故只有当轴压比在中高值（0.7～1.0）时，截面尺寸效应对试件的安全储备系数有减小现象。

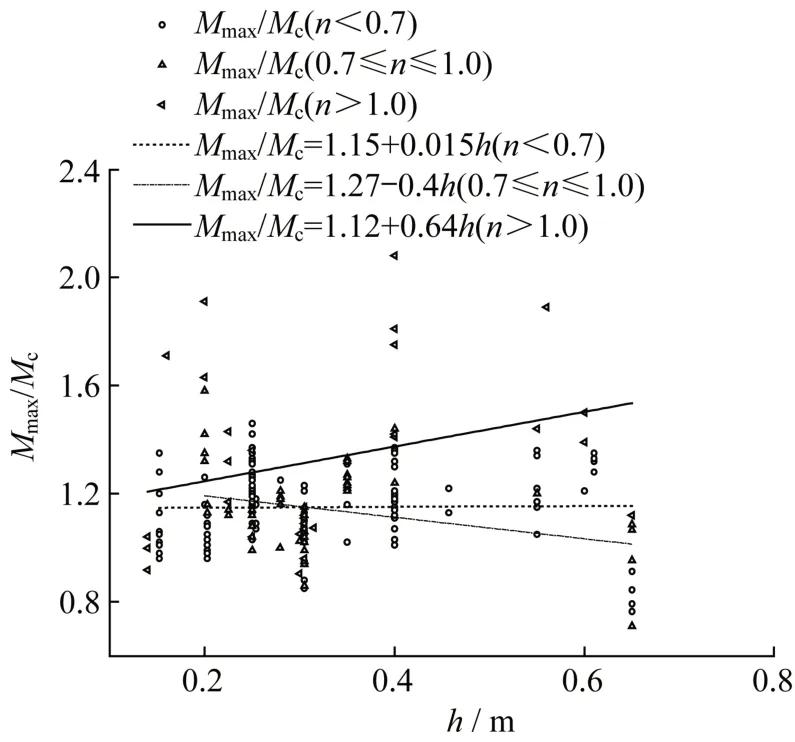
图10 安全储备系数与截面高度之间关系Fig.10 The relationship between safety reserve coefficient and cross section height

收集的试件中183 根为方形截面柱，35 根为矩形截面柱。对于方形截面柱，截面尺寸效应与截面面积或者截面高度的变化规律是一致的，而对于矩形截面柱，截面尺寸效应还应该与截面宽度存在一定关系。通过分析35 根矩形截面柱试件的安全储备系数K与截面面积A、截面高度h及截面宽度b的关系，安全储备系数K与截面面积A、截面高度h及截面宽度b的有着相同的关系。为了更加全面考虑截面尺寸效应，图11 给出了试验柱的安全储备系数K与截面面积A的变化规律，从图11 可以发现，随着截面面积A的增大，当轴压比小于1 时，试验柱的安全储备系数K随之减小；当轴压比大于1 时，试验柱的安全储备系数K随之增大。

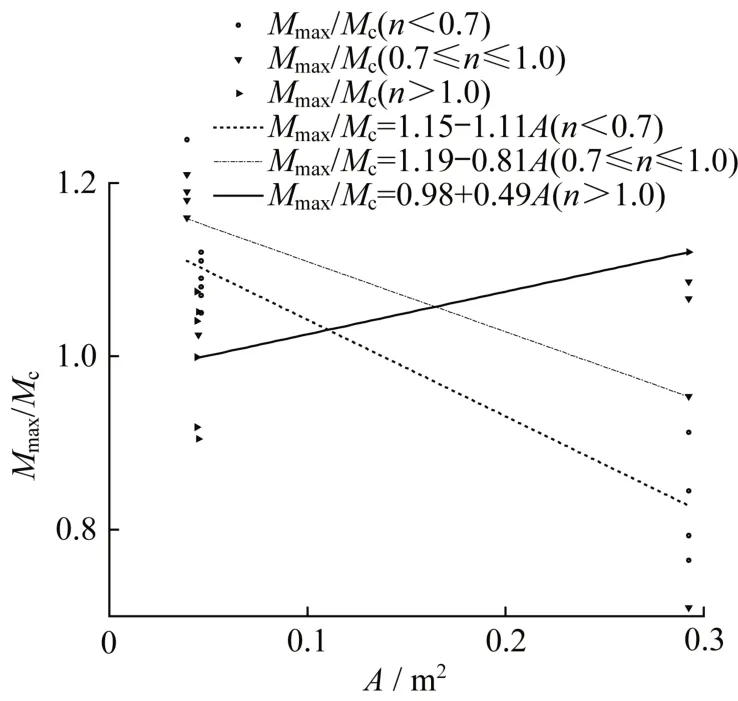
图11 安全储备系数与截面面积之间关系Fig.11 The relationship between safety reserve coefficient and cross-sectional area

3.3 规范公式的修正

从以上分析结果可知，当轴压比大于1 时，试验柱抗弯承载力随着截面尺寸的增大而增大，可以不考虑截面尺寸效应对柱抗弯承载力的影响。此外，从图10和图11看出，随着截面尺寸的增大，矩形截面柱的抗弯承载力较方形截面柱的抗弯承载力减低幅度较大，故矩形截面柱偏于不安全，截面尺寸效应更为明显。下面以大偏心受压破坏的矩形截面试验柱的试验结果，分析讨论考虑截面尺寸效应的大偏心受压破坏试验柱的抗弯承载力计算公式。

钢筋混凝土框架柱中钢筋的力学性能比较稳定，不会影响框架柱的抗弯承载力尺寸效应，因此柱抗弯承载力的截面尺寸效应是由混凝土引起的［12-13］，故建议修正的钢筋混凝土柱正截面受弯承载力计算式为

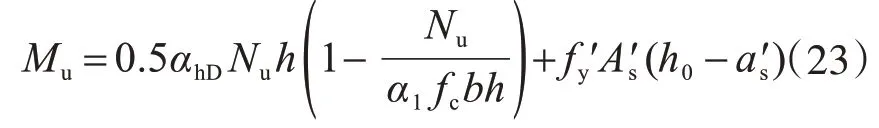
根据Bazan［3］理论，截面尺寸效应按照下式计算：

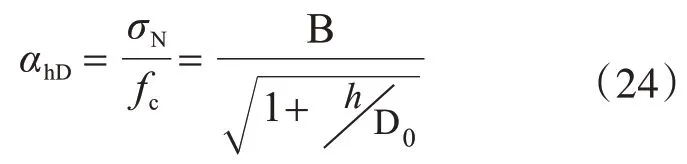
式中：σN为名义应力；B、D0为常数；fc为混凝土抗压强度设计值；h为构件截面高度。

根据大偏心受压破坏矩形截面试验柱的试验结果，并将其他参数代入到式（23）求得各试件的αhD值。令将式（24）转化为

根据大偏心受压破坏矩形截面试验柱的αhD值（当αhD≥1 时，取αhD=1）拟合式（25）求得B和D0分别为1.56和205，得到αhD值的计算公式为

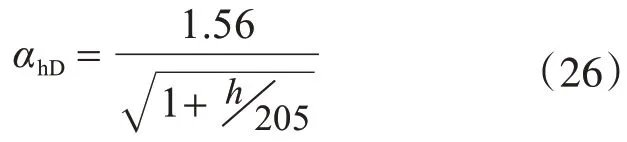
考虑到αhD的性质和小尺寸试件实际情况［13］，建议h≤300 mm时，αhD取值为

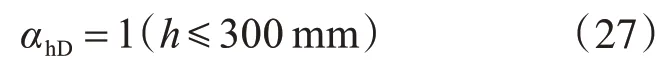
4 结 论

本文根据218 根钢筋混凝土试验柱发生弯曲破坏的试验结果，定量分析了截面尺寸对试验柱的承载力、延性、刚度及塑性铰转动能力的变化影响规律，然后在理论分析和试验结果分析的基础上，推出了考虑截面尺寸效应的钢筋混凝土柱正截面大偏心受压破坏的受弯承载力计算公式，主要结论如下：

（1）轴压比在中高值（0.7～1.0）时，试验柱的名义屈服剪力和名义极限剪力存在截面尺寸效应。当轴压比大于0.7时，试验柱的名义弯矩存在截面尺寸效应。

（2）当轴压比在0.7～1.0 时，截面尺寸效应对试验柱延性有降低现象。

（3）当轴压比大于1时，截面尺寸效应对试验柱最大刚度与弹性刚度比值和试验柱强化刚度与弹性刚度比值有降低现象。

（4）轴压比大于0.7 时，截面尺寸效应对试验柱塑性铰转角有降低现象。

（5）轴压比在中高值（0.7～1.0）时，试件的安全储备系数减小，表现出明显的尺寸效应。而矩形截面试验柱当轴压比小于1 时，截面尺寸效应对试件安全储备系数有降低现象。

（6）在理论分析和试验结果分析的基础上，推导出了考虑截面尺寸效应的钢筋混凝土柱正截面大偏心受压破坏受弯承载力计算规范的修正公式。当截面高度小于或等于300 mm时，钢筋混凝土柱正截面大偏心受压破坏受弯承载力不降低；当截面高度大于300 mm时，钢筋混凝土柱正截面大偏心受压破坏受弯承载力符合Bazan 尺寸效应理论。