基于换算剪力的变截面箱梁弯曲剪应力计算方法

2021-02-22张玉元张元海

东南大学学报（自然科学版） 2021年1期

张玉元张元海张慧

(兰州交通大学土木工程学院，兰州 730070)

大跨度混凝土箱梁桥下挠和开裂是制约其发展和应用的主要因素之一.国内外学者普遍认为，进一步优化薄壁结构剪应力计算方法对分析箱梁桥屈曲变形和挠度控制具有十分重要的力学意义[1-6].

目前，国内外学者对箱梁桥剪应力计算方法已开展了比较深入的理论和试验研究，同时也取得了一些对工程设计有指导意义的方法和结论.在试验研究方面，张哲等[7]以某工程单箱八室变截面PC组合箱梁桥为例，进行了实桥试验研究和有限元模拟，发现各腹板剪应力分配不均匀，在设计中应予以充分考虑；李海燕等[8]以运宝黄河大桥为工程背景，研究了单箱五室斜拉箱梁桥腹板的抗剪性能，得到混凝土腹板的剪力分配比重高于钢腹板；邓文琴等[9]以模型试验和数值模拟为手段，研究了内衬混凝土对变截面组合箱梁桥剪切和扭转性能的影响，发现内衬混凝土与钢腹板承剪比随荷载的增加而变化；崔学峰等[10]研究了内衬混凝土对波形钢腹板受剪性能的影响，并给出了内衬混凝土构造尺寸的优化建议.在理论研究方面，尼颖升等[11]运用空间网格法分析了多室组合箱梁的腹板剪力分配情况，揭示了横隔板处截面的剪应力分布规律；刘超等[12]在不考虑组合梁界面滑移的前提下，运用梁段微元法给出了组合箱梁的剪应力计算方法；李杰等[13-14]以理论推导和有限元方法为手段，计算分析了多种荷载作用下组合箱梁波形钢腹板的剪应力分布规律及其传递效率；王强等[15]在既有变截面箱梁剪应力计算方法的基础上，分析了悬臂板宽度和厚度、梁高、腹板和底板厚度及箱室宽度对腹板剪力流分配的影响；乔朋等[16]建立了单箱双室和三室波形钢腹板组合梁的有限元模型和试验模型，分析了横向对称和偏心荷载作用下波形钢腹板的剪应力分布模式，并揭示了其产生机理及分布规律；Zhou等[17]在分析变截面箱梁剪应力分布模式的基础上，结合力的等效原理给出了该箱梁剪应力的简化计算公式.上述文献对箱梁桥剪应力的计算方法已开展了比较深入的研究，但现有方法计算箱梁剪应力时过程较繁琐，不便于设计人员使用，尤其对于变厚度的变截面箱梁剪应力计算更是麻烦，因此需要对该方法做进一步优化和精简.

本文运用变截面梁段内力微分关系和微元体平衡微分方程建立箱梁剪应力的传统计算方法(即TCM法)；基于TCM法计算公式，分析变截面箱梁各项剪应力分布模式之间的相似关系，提出截面换算剪力的概念，并引入剪应力分项系数，建立变截面箱梁剪应力的简化计算方法(即SCM法)；以变截面悬臂箱梁为例，通过有限元解和TCM解来考证简化计算方法的正确性，并揭示各项剪应力沿截面横、纵向的分布规律.

1 传统计算方法

图1为受任意竖向对称荷载p(z)作用的变截面箱梁横断面简图.oxyz为右手直角坐标系，坐标原点o位于截面形心处，z为纵轴；b1、b2、b3分别为顶、底板半宽和悬臂板宽，hu、hb分别为顶、底板中面至形心轴的距离，h为顶底板中面之间的距离，tu、tb分别为顶、底板厚度，tw为腹板厚度，θ为腹板俯角；中面上的箭头表示剪力流坐标系(即s坐标系)，计算起点选在顶、底板中点和悬臂板自由端处，箭头指向表示静面矩积分方向，数字1～10表示相应的积分起止点.计算时假定箱梁弯曲剪应力沿壁厚均匀分布，则剪力流可表达为剪应力τ与壁厚t的乘积，即q=τt.

图1 箱梁横截面及坐标系

如图2所示，在变截面箱梁上取长度为dz的微段，图中M、Q、N分别为作用在梁端的弯矩、剪力和轴力，α为两端横截面形心连线的水平倾角，β为梁底倾角.

图2 变截面箱梁微段受力图

运用力矩平衡条件可得内力的微分关系，即

(1)

式中，M为截面绕x轴的弯矩，其方向为梁体下侧受拉为正，受压为负；N的方向为压为正，拉为负；Q的方向为顺时针正，逆时针负.

由材料力学可知，变截面箱梁任一点的初等梁纵向应力σ0可表达为

(2)

式中，Ix为截面绕x轴的惯性矩；A为横截面积.

式(2)对z求一阶导，并结合式(1)可得

(3)

式中，A、y、Q、M、Ix都是关于z的函数.

如图3所示，在箱梁截面任意点处取壁厚为t的微元体dsdz，沿z向建立正应力与剪力流的平衡微分方程，即

(4)

对s积分可得

(5)

式中，q0为截面剪力流；qA为箱梁横截面顶板中点切口处的常剪流.

图3 箱梁任一点微元体受力图

由箱形梁理论可知，截面开口处的常剪流qA=0[18]，将式(3)代入式(5)可得变截面箱梁横截面任一点处的剪力流计算公式：

(6)

由剪力流与剪应力的关系，可得到变截面箱梁横截面任一点的剪应力计算公式：

(7)

即

τ0=τQ+τN+τM

(8)

由式(8)可知，变截面箱梁剪应力由剪力引起的剪应力分量τQ(等截面箱梁计算公式)、轴力引起的剪应力分量τN和弯矩引起的剪应力分量τM组成，这与等截面箱梁剪应力构成存在很大区别.

2 简化计算方法

为了简化变截面箱梁剪应力计算公式，需从TCM法导出的剪应力计算公式入手，发现各内力引起的剪应力分量沿横截面的分布规律，以此建立各项剪应力之间关系.然后，通过积分法导出各项剪应力沿腹板的合力(即换算剪力)，并将其代入等截面箱梁剪应力计算公式得到各项内力对应的剪应力分量，叠加后即可得到截面任一点的剪应力.

由TCM法导出的弯矩剪应力分量τM可知，在任意横截面z处，其几何参数Ix和I′x为常数，静面矩Sx和S′x是关于s的函数.由此可见，弯矩和剪力引起的剪应力横向分布模式之间存在一定的相似性.故运用积分法可导出弯矩剪应力分量的竖向合力QM(即弯矩换算剪力)，其表达式为

(9)

式中

将式(9)代入等截面箱梁剪应力计算公式可得弯矩剪应力分量τM的表达式：

(10)

为了研究各分项剪应力对总剪应力的贡献度，特引入剪应力分项系数χi，其定义为

(11)

式中，下标i取M、N，其符号含义与截面内力一致.

将式(10)代入式(11)可得弯矩引起的剪应力分项系数χM表达式，即

(12)

由TCM法导出的轴力剪应力分量τN可知，在任意横截面z处，其面积参数A、Aa、面积微分A′和惯性矩Ix均为常数，静面矩Sx为关于s的函数，故轴力和剪力引起的剪应力横向分布模式之间也存在一定的相似性.此时，可直接导出轴力剪应力分量沿竖向的合力QN(即轴力换算剪力),其表达式为

(13)

将式(13)代入等截面箱梁剪应力计算公式可得轴力剪应力分量τN的表达式：

(14)

将式(14)代入剪应力分项系数表达式(11)，可得轴力引起的剪应力分项系数χN，即

(15)

上述已通过简化计算方法(SCM法)导出了变截面箱梁弯矩和轴力引起的剪应力简便计算公式，则横截面任一点的剪应力可表达为

τ0=τQ+τM+τN=

(16)

根据变截面箱梁各项剪应力分项系数的定义，可导出变截面箱梁剪应力的另一表达式：

(17)

3 几何参数计算

图4 悬臂箱梁作用均布荷载简图

根据梁底曲线分布形式，可求出纵向任意位置处的梁高h(z)，即

(18)

截面积A和面积微分A′可表达为

(19)

式中，b2=b1-htanθ.

形心至上、下翼板的距离hu和hb可表达为

(20)

惯性矩Ix和微分关系I′x可表达为

(21)

1) 形心轴以上部分

在1→2段

在3→2段

在2→4段

2) 形心轴以下部分

在6→5段

在5→4段

4 算例分析

以文献[19]中介绍的混凝土变截面悬臂箱梁为例，梁高按一次线性分布，跨度为0.6 m，横截面尺寸如图5所示.自由端截面顶板肋处对称施加竖向集中荷载P=2×15 kN，腹板重心轴处对称施加轴向压力N=2×5 kN，弹性模量E=2.9 GPa，泊松比μ=0.375，剪切模量G=1.054 5 GPa.

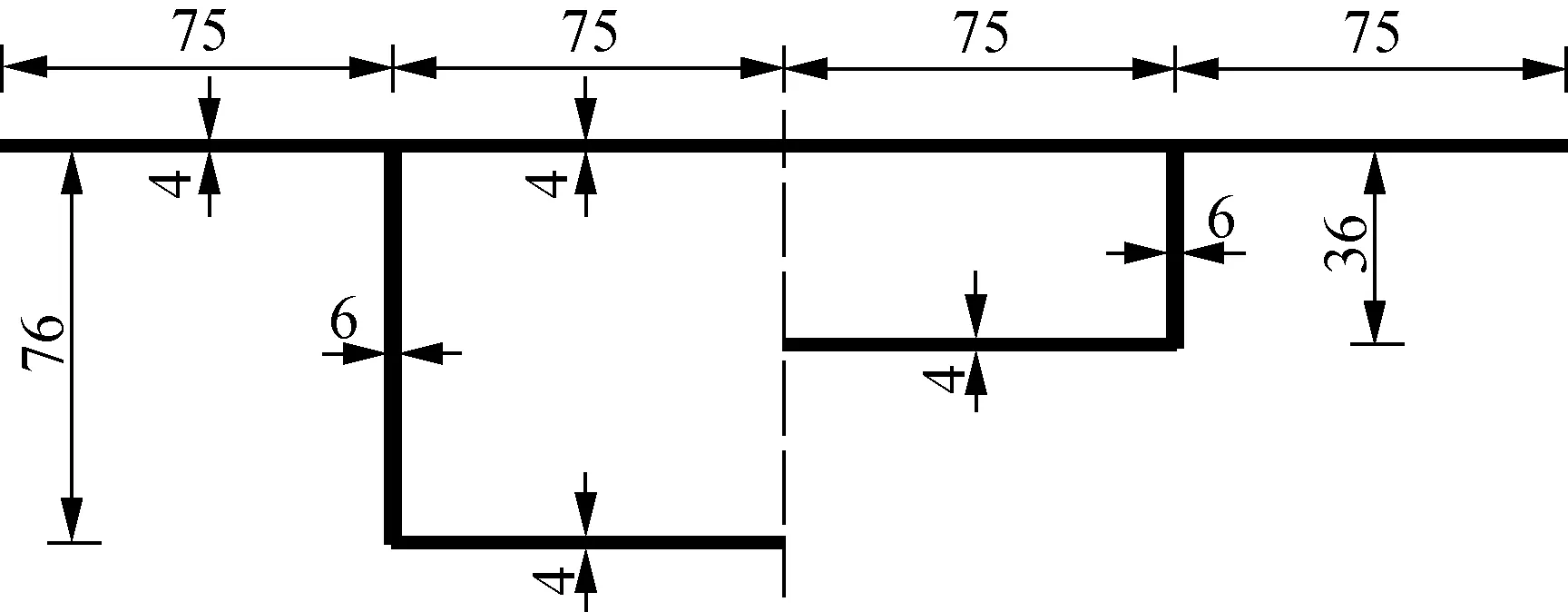
图5 变截面悬臂箱梁横截面尺寸(单位：mm)

运用ANSYS Shell63单元建立变截面箱梁有限元模型，如图6所示，该模型共划分为4 178个节点，4 160个单元.固定端截面约束x、y、z三个方向的平动自由度和转动自由度，计算并提取l/2截面的剪应力.利用本文TCM和SCM方法计算并绘制l/2截面的剪应力横向分布图、腹板重心轴处的剪应力纵向分布图及剪应力分项系数纵向分布图，如图7～图9所示；将截面关键点剪应力列于表1和表2，以便于对比.

图6 变截面悬臂箱梁有限元模型

(a) 顶板和悬臂板

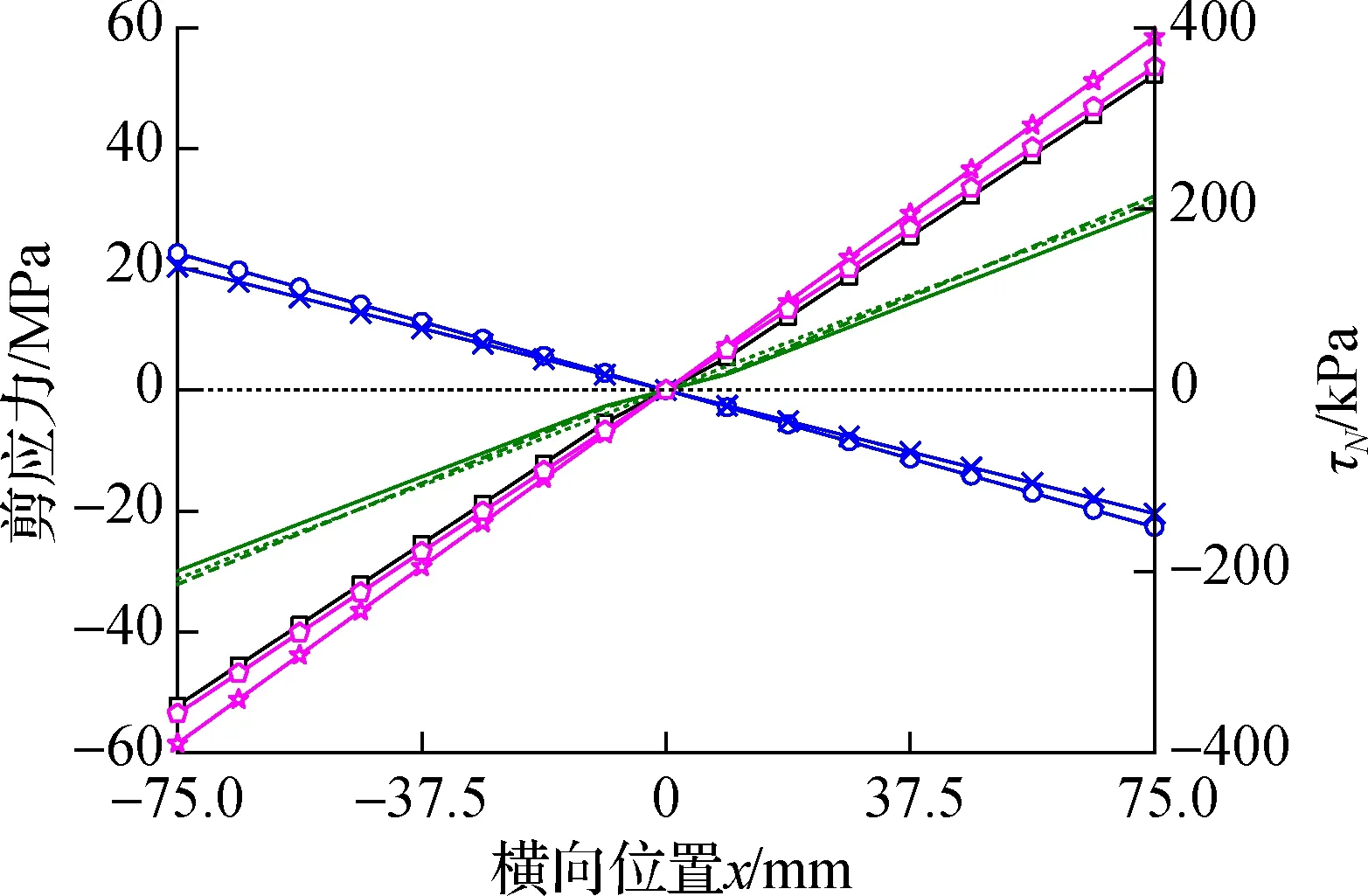
(b) 底板

图7 变截面悬臂箱梁l/2截面剪应力横向分布图

图8 变截面悬臂箱梁腹板重心轴处的剪应力纵向分布图

由图7和表1可知：悬臂板、顶板和底板上剪力、轴力及弯矩引起的剪应力沿横向呈一次线性分布，腹板上各项剪应力沿竖向呈二次抛物线分布；剪力、轴力引起的剪应力流向相同，弯矩引起的剪应力流向与前者相反，可见弯矩剪应力分量对总剪应力有一定的削弱作用.TCM和SCM法计算得到的总剪应力与有限元解吻合程度良好，2种方法计算的总剪应力最大误差为7.32%，进而验证了SCM方法的正确性.

图9 变截面悬臂箱梁剪应力分项系数纵向分布图

由图8和表2可知：在变截面悬臂箱梁腹板重心轴处，剪力、轴力引起的剪应力分量及总剪应力沿纵向呈递增趋势，弯矩引起的剪应力分量呈递减趋势；弯矩、剪力引起的剪应力分量远大于轴力引起的剪应力分量；SCM和TCM法计算轴力引起的剪应力分量存在一定的误差，二者最大误差为17.70%，其余内力引起的剪应力分量及总剪应力吻合程度均良好.

表1 变截面悬臂箱梁l/2截面关键点剪应力对比

表2 变截面悬臂箱梁腹板重心轴处的轴力剪应力分量对比

由图9可知：弯矩引起的剪应力分项系数沿纵向逐渐减小，且其值小于零；轴力引起的剪应力分项系数沿纵向逐渐增大，且其值大于0；总分项系数大于0，且沿纵向呈递增趋势，在自由端其值接近于1，在此截面处可按照等截面箱梁剪应力计算公式求解；弯矩分项系数在总分项系数中占比较大，轴力分项系数占比甚小，因此在计算变截面箱梁剪应力时应主要考虑剪力和弯矩的影响.