面向计算思维培养的教学设计实践研究

张霖

【摘 要】计算思维是新课程标准下信息技术课程的核心学科素养，采用“一题多解”的方式来设计教学内容，可以有效地培养计算思维、拓宽思维广度和提高思维深度。本文以排序算法为例，设计一个“一题多解”的教学实例，以此论述基于“一题多解”思想的教学设计方法、策略和技巧。

【关键词】排序算法;一题多解;计算思维;教学设计

【中图分类号】G434  【文献标识码】A

【论文编号】1671-7384（2021）010-060-03

案例背景

随着2017版普通高中信息技术课程标准的发布，信息技术学科核心素养的理念也开始渗透到我们的课堂教学中来，为此浙江义乌市组织了一次面向计算思维培养，主题为“算法综合复习课”的教研活动。我准备了这节《基于一题多解的算法教学设计案例》专题复习课，作为公开课与市里的老师们开展交流研讨。

案例描述

课前我了解到学校里刚刚举办过校园艺术节，于是上课后，我借着艺术节的话题设置了如下的情境：我们班安排了若干同学参加学校的合唱比赛，比赛要求按照一定的队形来安排队列，队列的要求是：男生在左，女生在右，且整个队列从左向右看时，男生从低到高，女生从高到低。随后我提出了这节课的第一个问题：“若知道这些同学的身高（数组a、身高数值）和性别（数组b、“M”和“W”），用什么办法能够编程实现队列的排列呢？”

假設有10个学生，其身高与性别依次为：

162（女）、187（男）、155（女）、152（女）、166（男）、165（女）、177（男）、152（男）、160（女）、168（女）。

按照题目要求排成队列后的顺序为：

152（男）、166（男）、177（男）、187（男）、168（女）、165（女）、162（女）、160（女）、155（女）、152（女）。

学生很容易就想到了一个办法：先将男生从低到高排序，再将女生从高到低排序，然后先输出男生数组再输出女生数组，就能够实现了。我说：“对，那么请大家打开我们素材里的任务一，用冒泡排序算法将队列排出来。”

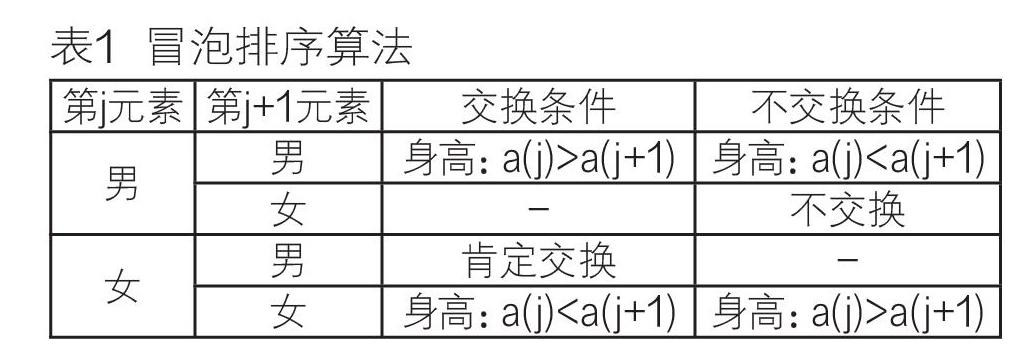
“已经有几位同学实现了，我们请实现的同学展示一下他们的结果。”我让一位学生演示了他的作品。随后我提高了问题的难度，提出了本节课的第二个问题：“同学们，刚才我们是写了两遍冒泡排序算法。那么有没有可能只用一个冒泡算法把队列排出来呢？”学生很明显被这个问题难住了，我顺势给出了一个表格：“其实冒泡排序的本质就是交换，请大家看看表格（表1），思考一下哪些情况是需要将元素交换，哪些又是不用交换的呢？”

学生完成了上述的表格后，总结出了三种需要交换的情况。

情况1：两个男生且前面的男生比后面的男生高。

情况2：前面女生且后面男生。

情况3：两个女生且前面的女生比后面的女生低。

“好，那么请大家根据这一总结，打开我们素材里的任务二，试着完成程序填空并运行实现。”我接着说。学生在前面讨论和总结的前提下，顺利地完成了任务二，并且有部分学生已经开始思考后续的任务。在大部分同学完成任务二后，我又提出了这节课的第三个问题：“同学们，既然能够用一个冒泡排序来解决这个问题，那么有没有可能用一个选择排序来解决呢？”由于前面问题的顺利解决，这个问题学生明显更愿意来思考和讨论，有学生提到可以在选择排序的过程中，保存下最矮男生和最矮女生的位置，并将他们交换到两头来实现。我就根据他们的想法在黑板上画出了算法实现示意图。

“第一轮的时候，我们用p来保存最矮男生的位置、q来保存最矮女生的位置，然后将他们交换到队伍的两头;第二轮的时候，我们再找次矮的男女生位置，再交换到两头第二个位置，以此类推是不是就可以实现用一个选择排序就排好顺序了。”我总结了刚才学生的思路，也顺势提出了更深层次的问题：“但是这样做，真的没有问题吗？”有学生就举手提出了问题：“如果最矮女生的位置就在队伍前面，那不是就会被换到最矮男生的位置上了吗？”“对，这位同学的问题提得非常好，也说明大家开始用算法思维来考虑问题了。那么，我们应该如何解决刚才同学提出的问题呢？”学生们经过讨论和思考后，提出了解决方案：当我们要换最矮的女生之前，先判断一下她原本是否在队头上;若是的，则需要修正一下位置。

结合学生的讨论，我又进一步分析出了这个算法还存在一个特殊情况需要处理，就是“男女生人数可能不一致，如何协调每次交换后p和q的起始位置”。解决方案也很容易被学生总结了出来：每次排完后，根据选出的结果来确定是否要让变量p、q的起始值为+1或-1。

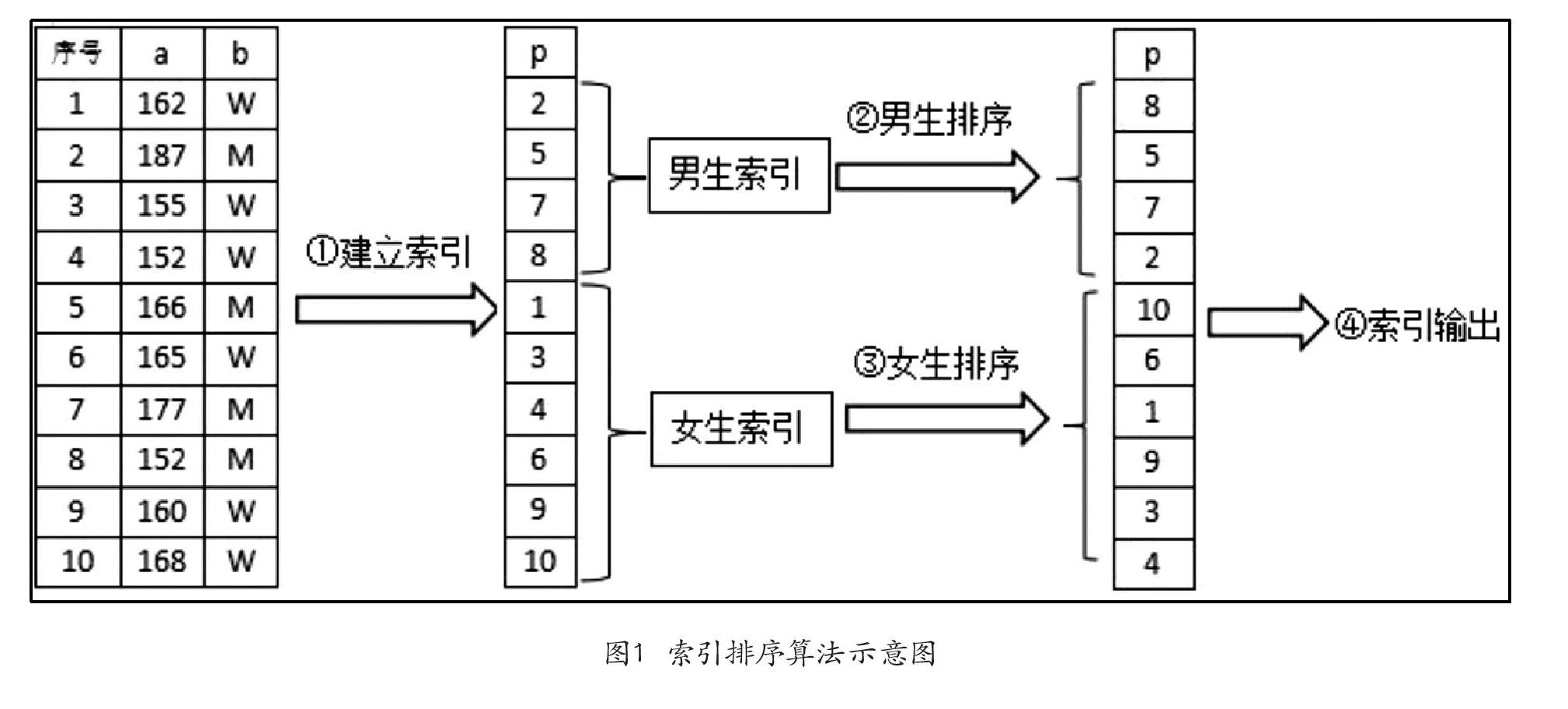
接下来，学生们根据刚才的讨论和分析，完成了素材里面的任务三。最后，我给出了本节课最难的一个问题：“如何用索引来减少排序时交换的次数？”并且直接给出了利用索引来排序的算法实现示意图。

由于有了前面三个问题的解决，学生对于第四个问题的思考显然深入了很多。我们首先抽象出了一个数组p来保存所有人的序号，那么交换的时候所要比较的对象就变成了“a（q（j））”和“a（q（j+1））”，突破了这一难点后，学生很容易就完成了素材里任务四的程序填空，并调试运行加以实现。

最后，我对这节课的内容进行了总结，由“基础冒泡的应用”→“冒泡排序本质的讨论”→“选择排序的变形”→“辅助索引数组的引入”，通过一个问题的不同解法，将排序算法中涉及到的各种算法模型进行了强化和总结。

案例反思

在本节课的教学设计中，我关注了以下4个设计要点。

1.思维难度的渐进式设计

学生对于任何内容的学习都应当遵循由易到难的原则，本文所提的4个解法就遵循了由易到难的递进顺序，先从基于基础算法的“先分类，再排序”的思想引入解法1，再到将解题思路限制于一个冒泡/选择排序的解法2与解法3，最后递进到基于“索引”的解法4，算法思维深度逐级递进，让学生在解决问题的过程中对排序算法的理解逐步加深。

2.思维表达的具象化设计

计算思维培养的关键，在于如何引导学生思考并将思考的要点呈现出来。在本节课中，我采用了多种方式来表达思维过程：比如问题1，由于问题难度较低，我采用总结性的语言将算法概括了出来;而到问题2，由于情况较多，我采用表格的方式将思维要点分类并呈现;对于较难的问题3和问题4，则采用图示的方式，利用框图、线条、序号等符号将问题解决的抽象过程呈现了出来。

学生在这些算法呈现的基础上，再将算法步骤归纳就容易了很多，也让抽象的问题解决过程具象化，起到了很好的学习支架功能。

3.教学组织的多样性设计

一节课的课堂节奏会直接影响学生的学习兴趣和学习效果。本节课在“讲”与“做”、“问”与“答”、“看”与“写”等问题的解决过程中，贯穿了四次问题分析、四次解法讨论和四次程序实例编写，做到了课堂组织的张弛有度，达到了教学过程的收放自如。虽然问题难度在加深，但是由于学生在看、想、说、做等思维活动过程中的有序切换，使得学生学习时不至于太过疲劳，也有效地提升了学生对于算法学习的兴趣度和参与感。

4.算法题目的有效性设计

不同难度和不同层次的算法思维，应当采用不同方式的题目设计来表现。比如本文中的解法1，由于难度较浅且使用了学生普遍掌握的算法模板来实现，教师可以采用让学生自主完成代码编写并调试的方式来设计题目。又比如解法2，就比较适合采用程序填空的方式来设计题目，让学生在透彻理解算法的基础上，通过阅读理解代码来归纳算法的实现过程，进而推演分析出空白处的代码内容。再比如解法3，由于不同过程有较大的相似性，可以采用给一个过程，让学生构造另一个过程，整块代码重写并调试的方式来设计题目。最后，如解法4这类思维深度较深的算法，不易直接让学生构造和编写，而应该采用部分代码挖空的方式来设计题目，通过题目的完成情况来验证学生对算法理解是否正确。

“一题多解”的教学设计方法可以广泛应用于算法思维的课堂教学中，采用这种方式设计的学习内容，能够有效培养学生构造算法模型的基本能力，在提升学生算法思维深度、拓宽算法思维广度等方面具有明显的作用。

作者单位：浙江义乌市教育研修院