球头铣刀切削加工表面形貌仿真技术研究
2021-10-19程德俊全宏杰张春燕
程德俊,全宏杰,张春燕
(江苏科技大学 机械工程学院, 镇江 212100)
铣削作为基本的加工工艺[1-2],广泛用于航空,汽车和精密模具等领域,其中球刀因加工对象适应性强等特点经常被用于重要零件复杂型面的铣削中.由于球头铣削通常应用于复杂曲面的精加工中,对工件的表面质量要求很高.并且,球刀切削部分的几何形状复杂,切削时切削刃与工件之间的接触点因刀具倾角变化而不断变化,铣削过程中的动态特性比较复杂[3],通过传统切削试验和仿真软件等方式来研究其加工过程中表面质量已不能满足现状,因此,有必要构建一种适用于球头铣刀一系列切削条件下的工件表面粗糙度高精度预测模型.
国内外很多学者都对球头铣削加工表面形貌做了深入的研究.文献[4]基于时间步长法,提出了一种改进的Z-MAP算法模拟球头铣削后的零件表面形貌,并且通过该表面形貌仿真方法研究每齿进给量、横向切宽和切削刃初始相位差等工艺参数对表面形貌和表面粗糙度的影响;文献[5]利用20组实验数据分别拟合出进给、横向方向的表面粗糙度与变形、切削参数之间的数学模型,从而实现对工件表面质量的预测;文献[6]提出了一种球头铣刀表面形貌模型,用于研究表面局部几何形状、刀具刃口形状、路径间隔以及刀具工件的相对运动等因素对球头铣刀表面形貌模的影响规律,通过切削试验验证了该模型准确性;文献[7]提出一种球头铣刀表面形貌模型,以分析进给速度、切削刃数、横向切宽、切削深度以及刀具跳动等因素对球头铣刀表面形貌的影响规律,并且通过在不同切削条件下的五轴球头铣削实验,验证了所构建的预测模型准确性;文献[8]在薄壁件铣削系统动力学的切削刃运动模型的基础上,建立了表面形貌仿真模型,用于分析系统振动对工件表面形貌的影响;文献[9]分别采用积分法、相关分析和傅里叶分析法对工件表面形貌进行研究,并且基于切削试验分析了主轴转速、每齿进给量对表面形貌的影响.上述模型其适用范围都比较窄,只能适用于特定的加工工况,并且都很少考虑刀具倾角的问题.
针对五轴机床加工过程中刀具接触点连续变化导致工件表面形貌预测不精确的问题,文中提出一种基于切削刃运动轨迹的球头铣削加工表面形貌预测模型.首先考虑刀具几何形状、表面倾斜角以及切削工况,建立球头铣刀运动轨迹公式;其次使用Visual C++语言开发表面形貌仿真软件;最后为验证模型预测精度进行了切削加工验证试验.对比结果表明,表面形貌仿真预测结果与试验数据具有很好的一致性.因此,所建模型可用于多轴加工过程中球头铣刀加工表面形貌的精准预测.
1 刀齿运动轨迹方程建模及表面形貌仿真
通常情况下球头铣刀加工时,其工件表面粗糙度往往都可通过近似球面模型计算求得,特别是当纵向进给量特别小时,运用球面近似模型所算表面粗糙度与实际加工表面粗糙度具有较好的吻合度.但当纵向进给量较大时,由于刀具做摆线运动,工件表面就会出现刀具中心处残余高度高于传统的残余高度,此时球面近似模型就不再适用[10].刀具运动有直线和旋转运动两部分组成[11],因此要想精确预测大纵向进给量工况下的工件表面形貌,就必须构建切削刃在工件坐标系中的运动轨迹.
1.1 球头铣刀的切削刃方程
图1是球头铣刀切削刃离散点模型,切削刃离散点n的方程为:
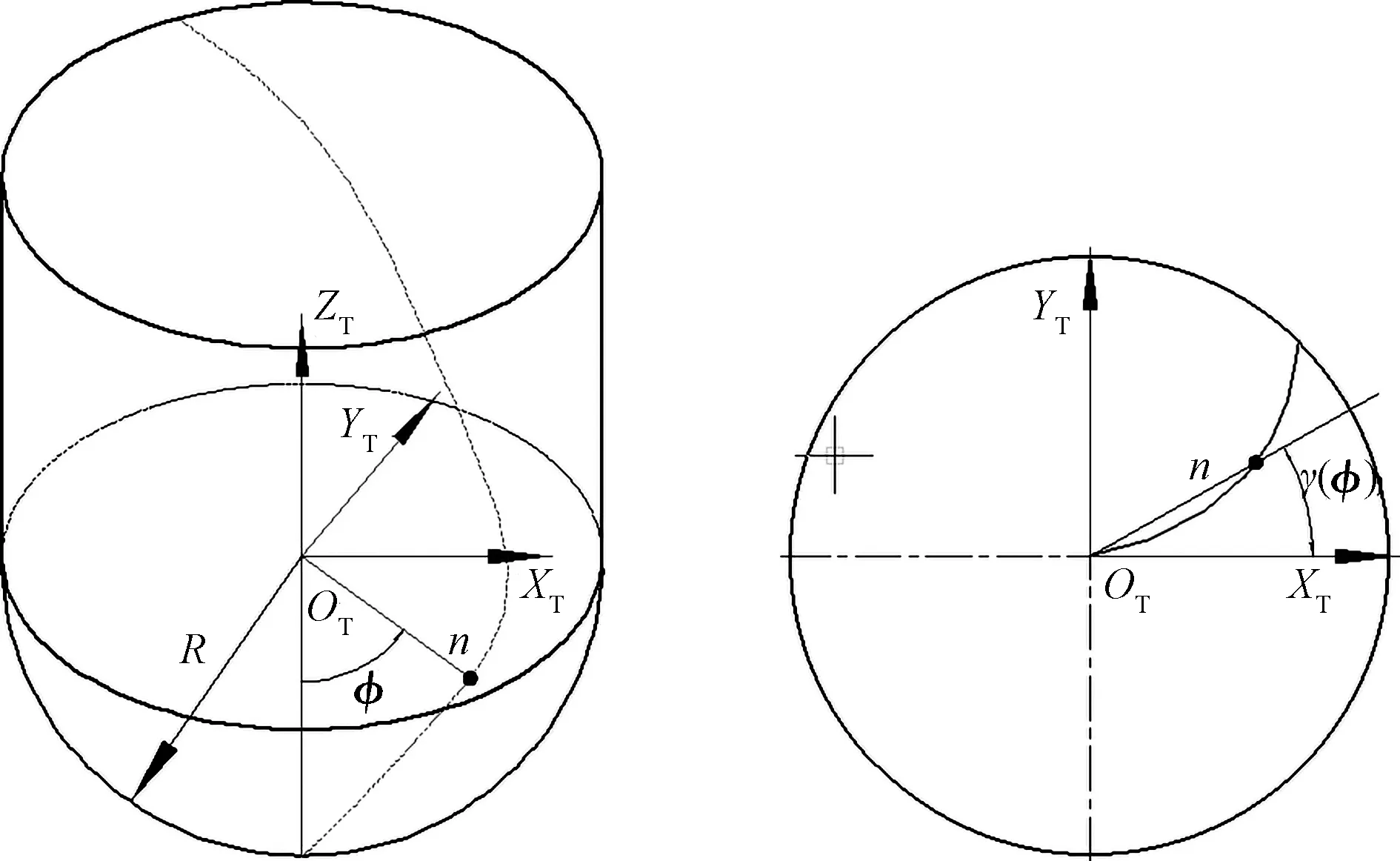
图1 球头铣刀切削刃离散点模型Fig.1 Discrete model of ball-end cutter
(1)
式中:R为球刀直径;Φ为离散点的位置角;βo为刀具螺旋角;j为刀具齿数序号,j=1,…,nf;nf为球刀齿数.
1.2 球头铣刀的运动轨迹方程
图2为切削运动坐标系,其中主要包含了4个坐标系:(1)刀具坐标系OT-XTYTZT,圆心OT位于球刀刀头中心处,ZT轴与刀具旋转轴共线;(2)刀具运动坐标系ON-XNYNZN,圆心ON位于球刀最低面,ZN轴与刀具旋转轴共线;(3)工件表面坐标系OR-XRYRZR,圆心OR位于球刀与工件接触点,ZR轴与工件表面垂直;(4)工件坐标系OW-XWYWZW,圆心OW为工件边界点,XW、YW、ZW与XR、YR、ZR平行.

图2 切削运动坐标系Fig.2 Cutting motion coordinate system
在刀具坐标系OT-XTYTZT中,将式(1)转换成齐次变换矩阵:
(2)
将刀具坐标系OT-XTYTZT转化成刀具运动坐标系ON-XNYNZN,就是将刀具坐标系沿ZT轴负方向移动R长度.因此,OT-XTYTZT转化为ON-XNYNZN的变化矩阵M1为:
(3)
球刀切削刃中n点的轨迹在刀具运动坐标系ON-XNYNZN可表示为:
(4)
如图2,图中球刀具有倾角δ.将刀具运动坐标系ON-XNYNZN转化成工件表面坐标系OR-XRYRZR,即将刀具运动坐标系绕YN轴旋转倾角δ.因此,ON-XNYNZN转化为OR-XRYRZR的变化矩阵M2为:
(5)
球刀切削刃中n点的轨迹在工件表面坐标系OR-XRYRZR可表示为:
(6)
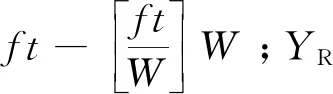
(7)
式中:f为纵向进给率;t为切削时间;W为工件宽度;ae为切削宽度;h为工件高度;ap为切削深度.
球刀切削刃中n点的轨迹在工件坐标系OW-XWYWZW可表示为:
(8)
球刀理论模型如图3,球刀的齿在铣削过程中既旋转又平移,铣刀中心的切削速度为0,并且随着半径的增加而增加.球刀中心附近的切削刃轨迹实际是摆线,可表示为:

图3 球刀理论模型Fig.3 Theory model of ball-end cutter

(9)
式中:r为切削刃半径;θ为旋转角;nf为切削刃齿数;R为球刀直径;Φ为离散点的位置角;βo为刀具螺旋角;j为刀具齿数序号;j=1,…,nf,nf为球刀齿数;δ为刀具倾斜角;f为纵向进给率;t为切削时间;W为工件宽度;ae为切削宽度;h为工件高度;ap为切削深度.
1.3 表面形貌仿真
采用二维网格平面模型作为工件模型,如图4[12].在工件坐标系OW-XWYWZW中,将工件模型划分为m×n个网格,将其定义为m×n零矩阵M;计算刀具沿轨迹运动时相应切削刃离散点的位置,求得每个网格中切削刃离散点的Z轴坐标值;通过比较每个网格中Z轴坐标值,获取最小的Z轴坐标值;最后将所得的最小Z轴坐标值组成m×n矩阵,替换原先的m×n零矩阵M.
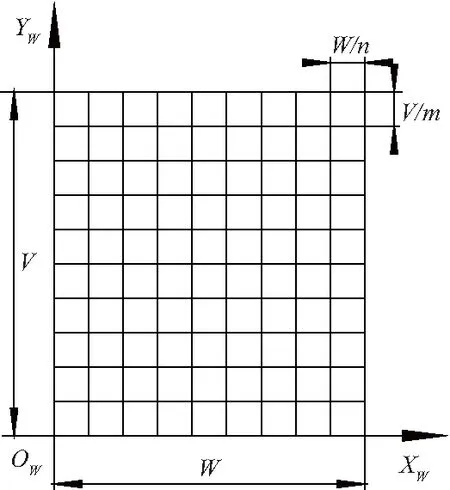
图4 工件模型Fig.4 Workpiece model
基于式(9),通过计算切削刃离散点在工件坐标系OW-XWYWZW中的运动轨迹,得到切削刃离散点在每个网格中的最小Z轴坐标值,进而更新原先的零矩阵M.基于新的m×n矩阵M,通过MATLAB软件进行表面形貌仿真.
根据三维算术平均偏差的定义[11],表面粗糙度为:
(10)
式中:m,n分别为工件坐标系OW-XWYWZW中沿XW,YW轴方向的网格数量;z(x,y)为采样点的坐标;h为参考平面方程.
表面形貌仿真过程都是基于切削刃运动轨迹方程,仿真工件表面形貌,并通过三维算术平均偏差的定义计算表面粗糙度值,流程如图5.
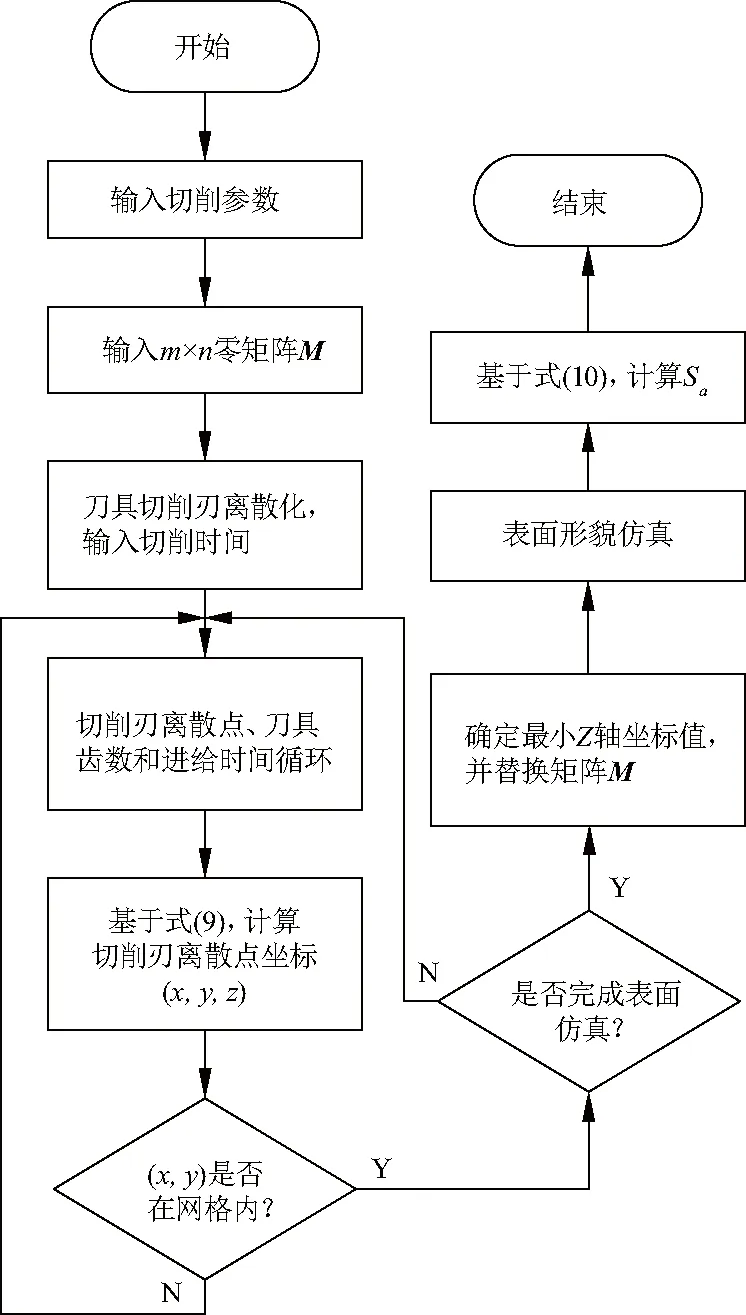
图5 仿真分析流程Fig.5 Flowchart of the simulation analysis
基于Visual C++语言开发了表面形貌预测软件如图6.首先输入刀具直径,切削刃半径和齿数,定义刀具的几何形状;然后输入进给量、主轴转速和切削宽度,确定工件切削条件;最后输入刀具或工件的倾斜角,即可输出加工表面形貌仿真结果,以实现加工前对工件表面质量的预测.
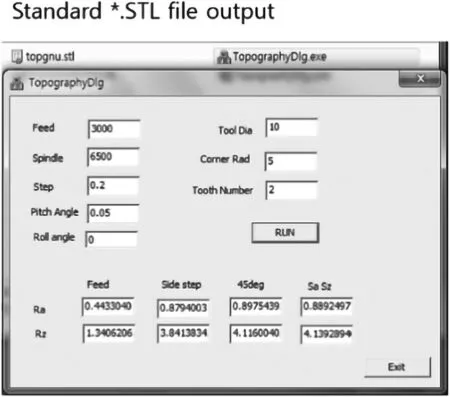
图6 微观表面形貌预测软件Fig.6 Surface topography simulation software
2 试验验证
2.1 试验设备及方案
为验证所构建的表面形貌模型正确性,通过铣削加工试验进行验证.试验选用HWACHEON VESTA 1000 三轴立式铣床进行加工,毛坯材料为45钢,尺寸为300 mm×70 mm×50 mm,刀具选用商用整体硬质合金球头铣刀如图7,刀具参数如表1,采用水平向下的铣削方式进行曲面加工[13].为了分析倾角对表面形貌影响,采用表2中加工参数[14].

图7 整体硬质合金球头铣刀Fig.7 Solid carbide ball-end cutter

表1 刀具参数Table 1 Tool parameters

表2 加工参数
2.2 表面粗糙度测量
工件加工完成后,利用粗糙度测量仪MITUTOYO SJ-210 取0.5 mm的取样长度对整个加工平面进行表面粗糙度Ra的测量,粗糙度测量仪MITUTOYO SJ-210的参数如表3.通过白光干涉仪(相干扫描干涉法)观察3D表面形貌图像,测量三维算术平均值表面粗糙度Sa.在扫描过程中,选择放大倍数为5.1的物镜,分辨率为1.66 μm,每个位置的扫描面积为0.9 mm×1.2 mm.扫描后,白光干涉仪提供加工表面的3D表面形貌,然后使用New View 7300系统计算三维算术平均值表面粗糙度Sa,New View 7300系统的性能参数如表4.

表3 MITUTOYO SJ-210参数

表4 New View 7300系统参数
图8为试验模具表面图,利用照相机变焦镜头在工件表面的不同点拍摄3次,得到3组测量数据.图9,10分别为位置1(0.06 °),位置4(0.24 °)处测量和仿真的表面形貌.

图8 模具表面图Fig.8 Mold surface picture

图9 位置1(0.06 °)处测量和仿真的三维形貌Fig.9 3D topography measured and simulated at position 1(0.06 °)

图10 位置4(0.24 °)处测量和仿真的三维形貌Fig.10 3D topography measured and simulated at position 4(0.24 °)
基于图9,10发现在多轴加工过程中,刀具倾角与三维表面粗糙度Sa之间呈反比关系.表5及图11为测量结果与模拟仿真之间的比较,结果表明模拟仿真结果与试验测量值具有较高的一致性.
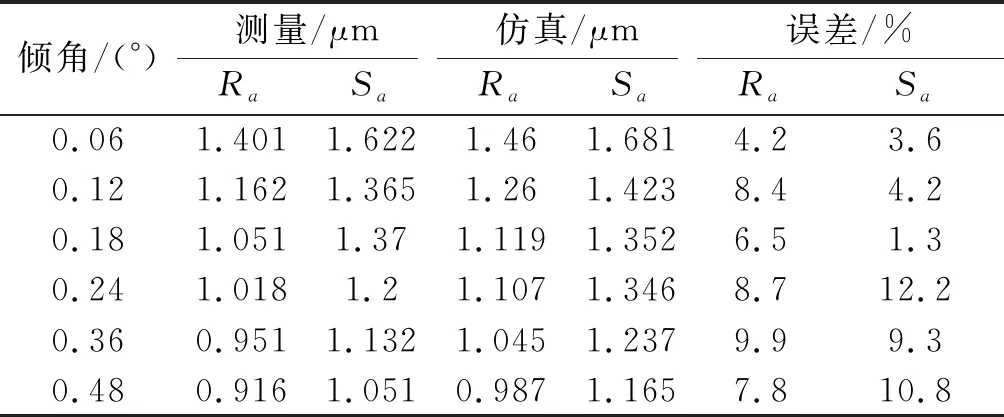
表5 实验与仿真表面粗糙度值比较

图11 试验与仿真数值比较图Fig.11 Comparison of experimental and simulated values
3 结论
(1) 在建立球头铣刀切削刃运动轨迹方程的基础上,通过计算切削刃离散点在工件模型中的坐标值,实现了球刀铣削表面形貌仿真,并基于Visual C++语言开发了表面形貌仿真软件.
(2) 基于仿真结果与实验测量结果具有较好的一致性,表明该预测模型的精度可靠.
(3) 研究结果表明在多轴加工过程中,随着刀具倾角的增大,二维表面粗糙度Ra和三维表面粗糙度Sa都下降.
(4) 在同一倾斜角下加工,工件的二维表面粗糙度Ra与三维表面粗糙度Sa相比,三维表面粗糙度Sa的值略大.
