船用柴油机凸轮轴形位误差非接触在位检测方法研究

刘云龙，李国超*，周宏根，陈浩安, 杨 飞，盖 文，卫国涛

(1.江苏科技大学 机械工程学院，镇江 212100) (2.陕西柴油机重工有限公司,兴平 713105)

实现大型凸轮轴的快速发展，关键在于提高其加工过程中的精度控制，以提高成品质量．传统的凸轮轴加工工艺是在完成每阶段的加工工序后，将凸轮轴从加工机床上取下进行检测．此种过程不仅给凸轮轴再次装夹在机床上加工带来了极大的不确定性，还使加工过程变得繁琐，从而极大地制约了凸轮轴的加工精度提升，降低了成品率．

目前，测量方式主要分为接触式测量和非接触式测量．其中接触式测量仪器主要采用感测接触头，其受环境中光照、油雾等影响较小，尤其以三坐标测量机为代表，精度保证较高[1]，但受其结构影响，大多应用于离线检测，需要提供非常好的检测平台．船用柴油机凸轮轴的尺寸往往超过很多检测仪器的量程，其长径比超过10 ∶1，长度在1 500 mm以上，一般的检测仪和检具都难以进行形位公差的直接测量．而非接触测量对于形位公差如跳动、同轴度等还有个难点便是如何实现基准的检测问题[2-4]．并且如何在复杂的生产现场、机床上安装检测仪器并能保证检测精度和实现多要素检测仍是尚未很好解决的难点．

在检测技术选择上，非接触式的激光检测技术，随着不断发展已较为成熟[5-7]，具有很高的直线性与超高的检测频率，在光学检测中检测精度很高[8]，受环境与工件材料影响较小，标定方法成熟[9]，成本低[10]，对物体的表面形貌有着精确的信号反馈[11]，同时传感器的安装自由度较高，应用灵活[12]，为在位检测提供了可能[13]．激光检测技术不仅可以利用自准直进行同轴度检测[14]，也可实时监测转轴在运行过程中的位置变化[15]，并且更广泛地用于轮廓扫描中[16-19]，通过三维扫描，获取检测物体的形状、尺寸等外在参数，也可以获得所设计的检测系统的世界坐标系[20]，从而获得检测物在检测系统中的三维坐标数据．再通过一系列的补偿方法[1，14]，或者巧妙的传感器设计来进一步提高检测精度[12，19]．但如何做到检测到工件的真实基准，克服环境因素、油污，实现在位检测仍是急需解决的问题．

文中分析了轴类工件的关键检测要素，依据这些检测要素构建检测系统、选择检测仪器，采用线激光测量仪与激光位移传感器进行组合，使用标定板对检测系统传感器进行标定零点和建立检测系统坐标系，通过对工件在检测系统的位姿分析，实现工件及装夹系统的坐标系标定．同时研究轴的基准及跳动、同轴度的检测原理，建立相应的检测数据处理算法，通过试验验证检测的精度与准确性．

1 轴类工件关键检测要素分析

轴类工件检测要素具有一定针对性，选取图1的凸轮轴为例(轴长l=1 000～2 000 mm，轴颈直径d=50～200 mm)，形位公差主要包括径向圆跳动、同轴度和轮廓度，其中当圆跳动被测要素为凸轮基圆时，基准为相邻轴颈构成的公共轴线，公差为0.015 mm；当圆跳动被测要素为轴颈时，基准为两轴端确定的公共轴线，公差为0.02 mm；同轴度被测要素为轴端凸台，公差为0.02 mm；轮廓度被测要素为凸轮部分，公差为0.05 mm．

图1 凸轮轴检测要素示意Fig.1 Schematic diagram of camshaft detection elements

轴类零件的检测过程中，作为其基准的理想中心轴线，是虚无的无法直接获得的空间轴线，也是非常难以测量与确定的．而且从误差的来源看，影响跳动量的也主要是横截面的圆度误差以及选择的轴线的偏移误差．因此在检测系统设计时，需要考虑如何确定基准，而传统的方法是利用V型块或者装夹工具的顶针，但却不可避免的引入回转误差和定位误差．

2 检测系统建立

在检测系统的总体设计中，为了检测出虚拟基准轴线和轴的检测要素，文中采用线激光测量仪，通过轮廓几何特征检测出虚拟基准轴线．对工件在检测系统中的位置进行分析，通过空间几何理论和线激光测量仪检测并计算出测量轴与测量系统间的相对位置．如图2，线激光测量仪置于凸轮轴磨床导轨上对凸轮轴进行轮廓检测．

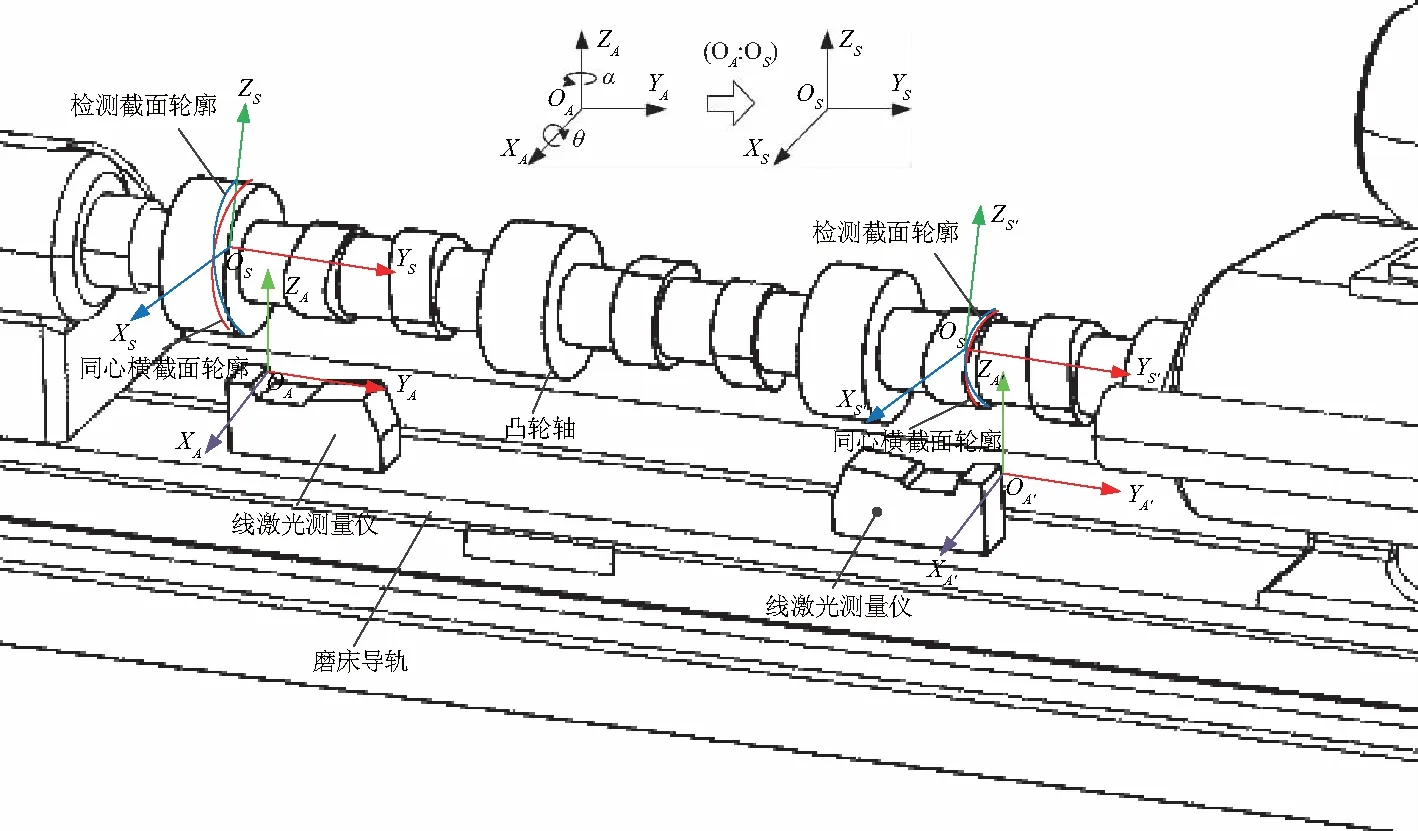
图2 工件在测量系统坐标系中的空间位置Fig.2 Spatial position of the workpiece in the coordinate system of the measurement system

为了减少测量系统有过多位置约束，文中只依靠导轨固定激光传感器并获取各传感器间的距离，没有与工件在各个方向上的精确约束，因此工件相对于检测系统可能存在多方向的位置偏移．

在检测系统坐标系中，工件存在绕X轴方向的旋转角θ，绕Z轴方向的旋转角α，绕Y轴方向的旋转角β；此由于激光传感器固定在导轨上，沿Y轴布置，加之线激光测量仪测量截面拥有XOZ平面的数据，而轴为圆柱件并沿Y轴旋转，因此在Y轴方向旋转角β可以不考虑．于是可建立检测系统坐标系OA-XAYAZA，其与以工件轴心轴线为Y轴的工件坐标系OS-XSYSZS间具有偏离量(x0,y0,z0,θ,α)，即检测系统坐标系中的点(x,y,z)分别在x，y和z轴方向上平移x0,y0和z0，然后绕X轴旋转角度θ，绕y轴旋转角度β，再绕Z轴旋转角度α后就能获得对应在工件坐标系OS-XSYSZS中对应的点坐标(x′,y′,z′)．因此检测系统坐标系和工件坐标系的变换关系为[16]：

(1)

3 系统标定

3.1 检测系统的坐标系标定

传感器在使用之前需要先进行标定，通常传感器校准有两种类型：一种是内部的，另一种是外部的．前者涉及传感器的光学和结构参数的校正，而后者则涉及应用场景下的标定与确定零点[21]． 在选择已经进行了内部的光学和结构参数的校正后的传感器后，需要对传感器进行外部标定和确定零点．

如图3，分别将线激光测量仪安装在长直导轨上，在测量方向前距离L处放置标定板，调节标定板标定平面与线激光测量仪光路正交．

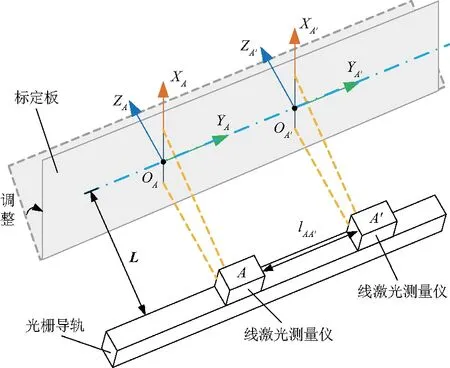
图3 检测系统坐标系标定示意Fig.3 Calibration of the detection system coordinate system

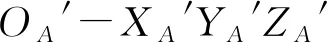
使用检测系统中的激光传感器获取到工件在OA-XAYAZA坐标系下的坐标数据,然后进行计算分析．此标定可避免引入线激光测量仪的安装位置误差，减小系统误差，同时无需采用多轴向工作台移动测量传感器的测量方法，使检测更加简易．

3.2 工件及装夹系统坐标系标定

根据空间解析几何理论，发现当轴杆类零件与测量系统既存在绕X轴方向的旋转角θ又存在绕Z轴方向的旋转角α时，线激光测量仪的光路所测的测量截面也是一个椭圆，其中椭圆的短轴亦是轴的直径，而不同的是椭圆的长轴ac不再沿着Z轴方向，短轴bd也不与X轴平行，如图4．

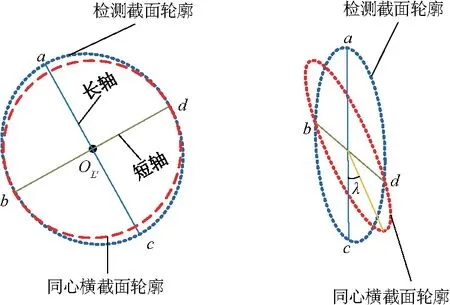
图4 绕X轴和Z轴方向的具有旋转角时检测截面Fig.4 Detection section with rotation angle around X axis and Z axis

此时所得椭圆轮廓的椭心也在中心轴线上，而且，椭圆轮廓的长轴和短轴亦对应着测量截面与横截面夹角，记为λ，大小为：

(2)

式中：lac为长轴长度；lbd为短轴长度.

根据线激光测量仪检测的截面轮廓以及在线激光测量仪坐标系内的轮廓点坐标，可以将工件在检测系统内的位姿加以明确，便于运算．

将高精度的圆柱量块置于装夹系统中，使用标定好的检测系统对圆柱量块进行检测，圆柱量块完全置于线激光测量仪的测量光路中，则圆柱量块与测量光路的相交截面为一高精度的椭圆轮廓，如图5．

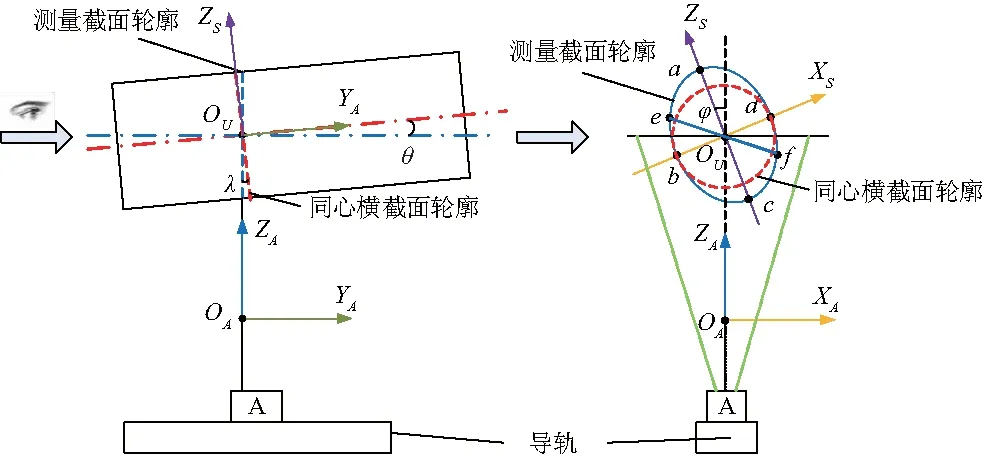
图5 线激光测量仪所测圆柱量块的截面坐标系Fig.5 Cross-sectional coordinate system of the cylindrical gauge block measured by the line laser measuring instrument

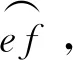
(3)

依据最小二乘原理，所拟合的目标函数为：

f(A,B,C,D,E,F)=

(4)

欲使f为最小，需使：

(5)

由此可得一个线性方程组,然后求解线性方程组就可以求得方程系数A,B,C,D,E,F的值．

假定椭圆的几何中心OU的坐标为(xU,zU)，则可求出：

(6)

(7)

同时长轴长度lac和短轴长度lbd分别为：

(8)

(9)

则椭圆在OA-XAYAZA坐标系中椭圆长轴的旋转角φ为：

(10)

由于在装夹系统中圆柱量块与检测系统具有上述的位姿，因此圆柱量块的测量截面与其同心横截面存在的夹角λ，根据式(2，3，8，9)可求出．

测量截面A的短轴，亦是同心横截面的直径，于是以bd为工件装夹系统坐标系的XS轴，以测量截面轮廓中心亦是同心横截面的圆心OU为工件装夹系统坐标系的原点OS，以垂直于圆柱量块横截面A的轴心轴线为YS轴，建立符合右手规则的工件装夹系统坐标系OS-XSYSZS．于是检测系统坐标系OA-XAYAZA与工件装夹系统坐标系OS-XSYSZS间具有偏离量为(xU,0,zU,φ,λ,0)，因此检测系统坐标系和工件及装夹系统坐标系的变换关系可由式(1)推导为：

(11)

由此，可以对工件及装夹系统的坐标系进行建立和标定，此标定亦可以获取装夹系统的将检测系统所获取的测量数据在工件及装夹系统坐标系中进行转换，由此也可将工件进行三维重建．

4 实例分析

对某一轴颈直经为φ150 mm的凸轮轴件进行测验(图6)，凸轮轴跳动公差要求为0.05 mm，同轴度公差要求为0.05 mm，凸轮轮廓度要求为0.08 mm．于是根据检测凸轮轴大小，检测装置的线激光测量仪选取某LJ-X8400型，可测最大宽度80 mm，z轴精度为1 μm．

图6 凸轮轴在磨床内装夹加工Fig.6 Clamping processing of the camshaft in the grinder

基准轴段测量截面轮廓点每次取3 000个轮廓点坐标数据；需要检测跳动t的轴颈与凸轮基圆采用线激光位移传感器仪检测，每组测量截面取20个测量点位移数据进行径向圆跳动计算；需要检测同轴度Φt的测量段采用线激光测量仪进行检测，每组取5个测量截面轮廓点数据进行同轴度计算；需要检测轮廓度的凸轮采用线激光测量仪进行检测，截面轮廓取3 000个坐标点并转换到工件坐标系统下；经过测量系统算法处理，得到测量结果，同时与三坐标测量值作比较，部分数据如表1.

表1 凸轮轴检测结果部分数据

实验中对凸轮轴进行多次测量，分析结果可以看出,凸轮轴在位测量系统的最大偏差在0.007 mm以内,在实验中测量系统的总体偏差在0.003 mm以内,因此该测量系统可以满足凸轮轴检测精度0.01 mm的要求．系统测量结果的均值与三坐标测量结果十分接近，偏差在2%左右，从检测结果的趋势来看，测量结果的波动较小，较为稳定，如图7．

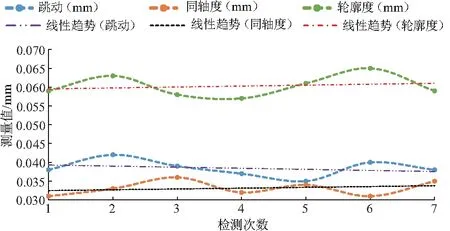
图7 凸轮轴检测结果趋势图Fig.7 Trend of camshaft inspection results

此外，通过实验发现，采用文中对轮廓数据进行椭圆算法处理、寻找圆心与长短轴比采用圆的算法处理、寻找圆心与半径所获得的结果精度更高；其中对于直径φ200 mm的工件跳动精度提高0.001 mm，直径精度提高0.015 mm．而且随着工件尺寸的增大，以及工件在测量系统中的偏转角度的增大，椭圆的算法精度比圆的算法精度提高的更多．

5 结论

文中提出了一种利用线激光测量仪对船用柴油机凸轮轴形位误差进行非接触在位测量的方法，基于空间几何理论，建立了系统模型并进行了原理分析，完成了在位测量中轴与测量系统位置检测、测量系统坐标系建立与统一、工件及装夹系统坐标系的建立与标定．研究的方法具有以下优点：

(1) 鲁棒性强，有效避免了工件在检测系统中存在偏转与偏移的影响,以及工件存在两端顶针孔存在回转偏心的问题．而对于基准为非圆柱面轴线，存在一定偏差时，文中检测原理所获得的跳动与同轴度结果最大误差在基准偏差值的2%以内．

(2) 测量稳定，处理结果波动范围较小，其中跳动值稳定在0.038 mm，同轴度值稳定在0.033 mm，轮廓度值稳定在0.06 mm．

(3) 精度高，文中算法模型同比一般圆检测算法对于直径φ200 mm以上的工件跳动精度提高0.001 mm，直径精度提高0.015 mm．