高雷诺数圆湍潜射流的数值模拟研究

古 磊，陈 科*，盛 立，尤云祥

(1.上海交通大学 海洋工程国家重点实验室，上海 200240) (2.高新船舶与深海开发装备协同创新中心，上海 200240) (3.中国人民解放军92578部队，北京 100161)

二十世纪以来，研究工作者陆续在海洋遥感卫星捕获的图像上观察到了一类形状像蘑菇的结构．研究分析发现，这是海洋表面上形成的某种大尺度的相干涡结构，并且这种相干涡结构形成于海洋中的某种动量源．在密度分层流体以及密度均匀浅水流体中呈现为准二维的偶极子涡对或偶极子涡街结构，而在密度均匀深水流体中呈现为蘑菇状结构[1]．

已有研究表明，潜艇等水下航行体螺旋桨的运转对周围流场的扰动作用，等效于给周围背景流体传递一个射流动量[2]，并且这种射流可以简化为一圆管潜射流．另外，已有文献对船舶螺旋桨的射流理论进行了详细研究[3]，对圆管潜射流在浅水背景流场中的演化特性研究成为国际前沿热点课题，同时利用星载合成孔径雷达捕获海洋表面的大尺度涡结构，进而探测和感知水下潜在航行目标，对发展我国非声反潜探测技术具有重大的军事意义．

文献[4]指出，雷诺数小于300时为层流射流；雷诺数大于300时，射流的层流区随着雷诺数的增大而逐渐消失，最终变为完全湍流．背景流场的浮力效应或者浅水效应会对湍流潜射流的演化特征产生较大影响，进而有可能形成准二维的大尺度相干涡结构．

目前，对圆管潜射流在密度分层流体或者密度均匀浅水流体中的演化特性进行了大量的基础研究[5-6]，并观测到了大尺度的涡结构．文献[7-9]对圆管潜射流在浅水密度均匀流体中的演化进行了实验研究，指出大尺度涡结构的形成与否主要与无量纲的水深约束参数C有关，并根据水深约束参数C的大小，将实验研究中的各个工况进行归类，按照水深约束参数C的区间从小到大依次为深水特征工况、过渡特征工况以及浅水特征工况，其中在浅水特征工况下有准二维的偶极子涡结构形成．

随着计算机技术的迅速发展，计算流体动力学(CFD)方法被广泛应用到了流体力学数值研究领域[10-13]．文献[13]采用CFD方法，定量研究了层流圆管潜射流在深水密度均匀流体中形成的蘑菇状涡结构的包络外形长度、螺旋形涡环半径、无量纲射流长度等3个几何特征参数随时间变化的一般规律．文献[14]采用CFD方法，定性和定量研究了层流圆管潜射流在浅水密度均匀流体中形成准二维大尺度涡结构的速度场与涡量场的演化规律．

迄今为止，运用计算流体动力学方法对真实尺度下的高雷诺数圆管潜射流在自由表面作用下的浅水密度均匀流体中演化特性的相关研究鲜有报道．有鉴于此，文中将针对这种情形下的湍流射流涡核演化特征、背景流场的垂向速度场与涡量场的变化特征、自由表面流场的变化特征等几个方面进行数值模拟和研究分析．

1 数值方法

结合文献[15]的实验研究，对于潜艇的阻力动量JD，有JD=CDV2S/2，其中：CD为阻力系数；V为潜艇航速；S=πD2/4为潜艇横截面积.设想了实尺度下一艘横截面直径D为20 m，水下航速为20 kn的潜艇在自由表面下潜深较小处的浅水环境中做悬停运动，其螺旋桨旋转作用产生的射流将传播至自由表面并在水面上留下可以被探测到的流场特征，这时潜艇螺旋桨后的射流动量J与其阻力动量JD相等，即J=JD，并由公式Re=J1/2/ν，ν为运动粘性系数，求得航行时的雷诺数为108，因而螺旋桨后动量尾迹的雷诺数约也为108，属于高雷诺数的范畴.在研究中采用圆管潜射流来等效等螺旋桨的尾迹射流．

将一个空心的射流圆管置于一个矩形流场中，圆管的一端位于矩形流场的左侧边界处，中心轴线位于矩形流场的中纵剖面上．坐标原点O设置在射流圆管出口的中心点，建立空间坐标系(图1)，其中Ox轴位于射流圆管中心轴线处且沿射流方向(即向右)为正，Oz轴竖直向上为正，Oy轴以垂直纸面向里为正．z=0平面为过射流圆管中心轴线的水平面，y=0平面为矩形流场的中纵剖面．设置射流圆管长度为L0，直径为D．将L0与D的关系设置为L0=10D．设置矩形流场长为300D，宽为200D，水深为50D，空气层为5D．将射流圆管的中心轴线置于潜深为水深处/51，即z=10D平面为自由表面，z=-40D平面为底部边界平面．取射流圆管的管径为D=2.00 m．

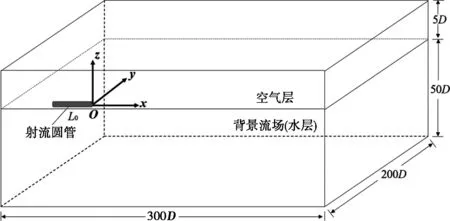
图1 矩形流场计算域示意图Fig.1 Sketch of the rectangular computation domain

将矩形流场划分为六面体的结构化网格，同时在射流的主流动区域进行局部网格加密，网格示意如图2．其中，图2(a)为整个矩形域网格的俯视图，图2(b)和图2(c)为圆管周围部分区域网格示意图(图中的白点表示射流圆管的横截面)，图2(d)为圆管横截面网格示意图．

图2 矩形域网格划分Fig.2 Grid configuration of the computation domain

圆管湍流潜射流的整个流动过程涉及到两个不同的阶段，首先是圆管湍流射流阶段，其次是射流停止之后的流体在背景流体中的演化阶段，把射流停止时刻t=Tinj(射流特续时间)作为上述两个阶段的分界时刻．在圆管湍流射流阶段，采用基于Realizablek-ε的雷诺时均(Reynolds average navier-stokes，RANS)湍流模型[11]；射流停止后，采用大涡模拟(large eddy simulation，LES)方法[13]来模拟大尺度涡在背景流体中的演化．这种考量的原因在于，射流持续阶段主要是经典的圆管出流问题，一般用RANS求解即可，而射流停止后，研究重点是演化过程中出现的大尺度效应和拟序结构，故采用大涡模拟方法．

使用Ansys Fluent软件对上述问题进行求解．为了实现对自由表面运动的捕捉，计算时采用了自由表面运动处理技术的VOF方法。将射流圆管的左侧端面设置成速度大小为u0的速度入口边界条件，在射流持续到t=Tinj时刻时停止射流，此时将射流圆管左端面速度大小调整为0；矩形域除去射流圆管管口区域的左端面设置成速度大小为0的速度入口边界条件；矩形域的右端面以及两个侧壁面均设为自由出流边界条件，由于计算域设置较为充裕，边界条件的影响较为有限；矩形域的顶部平面(即空气层的顶部)使用钢盖假定；矩形域的(即自由表面)以及底部边界均设置为对称边界条件；射流圆管的内外壁设置为无滑移的壁面边界条件.以除去射流圆管管口区域的左侧壁面处速度入口边界条件作为流场计算的初始条件．

在圆管湍流射流阶段，采用壁面增强函数来消除管壁附近的局部速度不大但网格长宽比较大所带来的影响，采用三阶精度的QUICK格式来离散控制方程的对流项，并采用二阶中心差分格式来离散控制方程的扩散项，设置压力速度耦合方式为SIMPLE算法．将RANS阶段结束时刻的流场作为LES阶段的初始流场．在大涡模拟阶段，采用有限体积法来求解LES方程，运用SIMPLEC算法作为压力速度的耦合算法，使用三阶精度的QUICK格式离散控制方程的对流项，将二阶精度的Crank-Nicolson半隐式格式作为瞬态项的时间积分方式，并使用四阶中心差分格式离散控制方程的扩散项．在数值计算过程中设置初始的时间步长为5×10-5s，同时为了缩短整个模型的计算时间，定期观察模型计算过程中的残差收敛情况，以适当调大时间步长．

在数值计算中，设置圆管左端面射流初速度u0的大小为50 m/s，又射流圆管的管径D=2.00 m，由公式Re=Du0/ν求得射流雷诺数大小为108，与真实螺旋桨后动量尾迹的雷诺数对应．数值计算时将射流持续时间Tinj设定为10 s．

2 结果与分析

为方便与前人结果[13-14]进行比较，文中沿用无量纲射流演化时间t*为：

t*=t/Tinj

定义流场中某个截面i上的动能Ei(除以密度ρ)和动量Pi(除以密度ρ)的计算公式为：

式中：u、v分别为该截面上速度场的分速度；S为截面面积；dS为截面面积微元．

同样进行无量纲化，计算公式为：

基于高雷诺数下的圆管潜射流与自由表面相互作用的数值模拟结果，对湍流射流涡核演化特征、背景流场的垂向速度场与涡量场的变化特征、自由表面流场的变化特征等几个方面进行详细分析．

2.1 湍流射流涡核演化特征

在文献[7-8]的实验研究中，采用激光照明板照射含有荧光素的射流来追踪射流的演化，并通过在流场中植入某种软晶石颗粒来显示流线等可视化方法，对流场信息进行了定性研究；而在文献[9]的实验研究中，运用了高清数码摄像等技术来研究由蓝色染料和水配制而成的染色液射流的演化过程．

为了实现对这种湍流射流形成的拟序涡核结构的识别和可视化，这里参照了中采用的基于Q判据的涡核识别方法，Q>0表示有涡存在，并将该区域定义为相干涡结构的涡核．Q的表达式为：

图3给出了文中的高雷诺数工况在6个不同时刻涡结构形态的轴测．其中，图3(a)为射流刚结束的时刻，从图中可以看出，射流此时此刻仍保持着完整的球形冠状结构，与深水特征工况下的蘑菇形涡结构类似，具有明显的三维运动特征，这是因为在发展的早期，射流结构还没有触及到自由表面，没有受到自由表面的影响，射流的流动可以沿着其轴线在背景流场中自由扩散，这时和深水工况下的无边界空间中的圆管射流演化特性没有差别．

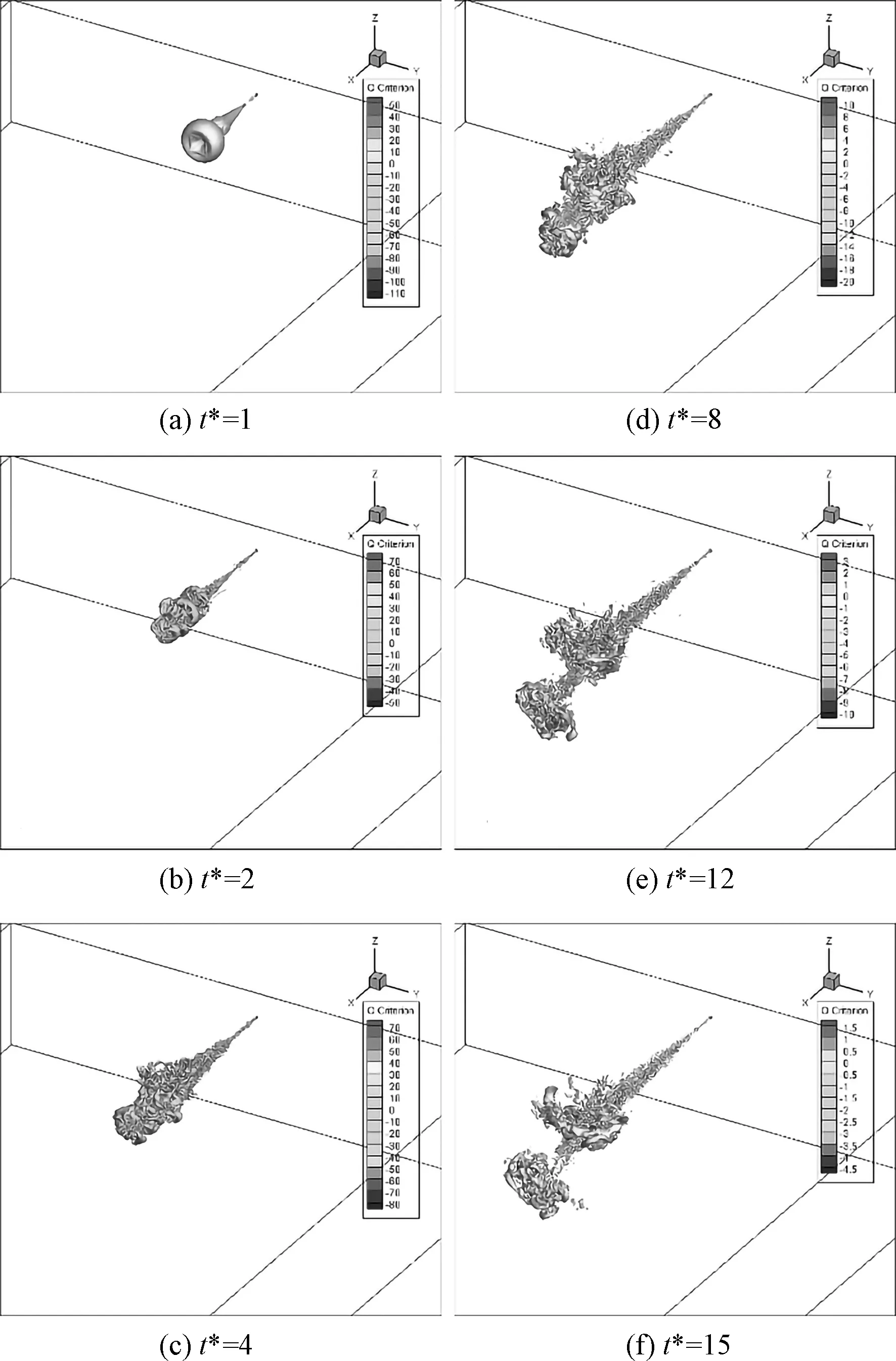
图3 6个不同时刻的涡结构形态Fig.3 Vortex structure at six different moments

为了更加清晰全面地表达湍流射流涡核的演化特征，图4给出了该6个不同时刻涡结构的横向以及纵向形态．由图3、4能够发现，按时间顺序射流结构逐步向四面八方扩散和发展，并从图4(b)开始接触到自由表面，进而受到自由表面的限制作用而横向扩散，涡结构的横向尺度逐渐扩大，表现出

图4 6个不同时刻涡结构的横向和垂向形态Fig.4 Transverse and vertical form of the vortex structure at six different moments

准二维的流动特征．同时湍流射流涡结构将其一部分能量传递给所接触到的自由表面的流体，这种能量传输作用使得自由表面上会形成若干涡对结构，这些涡对结构由于具有向前的速度进而随着时间的推移也逐渐向前移动．同时还发现从图4(d)开始，涡结构的前端开始出现明显的塌陷现象，并随着时间的推移有逐步脱离涡结构主体的趋势，这是因为射流涡结构的一部分流体在背景流体粘性剪切效应和自由表面的粘滞效应的双重影响下产生了与原来射流方向相反的流动．另外，图4(e)和图4(f)中的涡结构表现出了较高的相似度，说明涡结构从某一时刻开始达到了某种相对稳定的状态，并以这种相对稳定的结构继续发展．

2.2 垂向速度场与涡量场的变化特征

图5给出了背景流场中纵剖面上6个不同时刻的速度矢量图．由图可知，图5(a)中射流的流动还没有受到自由表面的影响，速度矢量场呈现出对称的分布，由于受到背景流体粘性剪切作用的影响，流体的速度矢量开始偏离射流最开始的方向，在上下方向上扩散，并形成局部微小的涡结构，如前面所述，这一时刻的流态和深水无限空间中的特征一致．

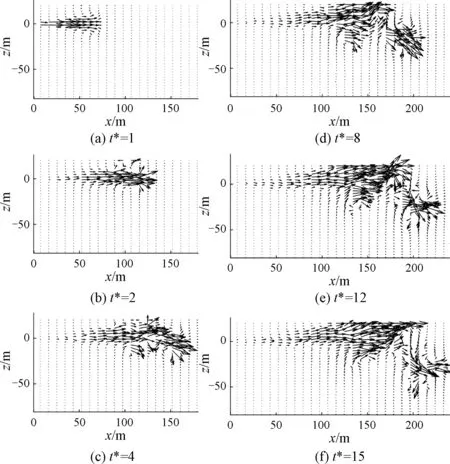
图5 中纵剖面上6个不同时刻的速度矢量图Fig.5 Velocity vector graphs (m/s) on the middle longitudinal profile at six different moments

从图5(b)开始，射流流动受到水面的影响，自由表面产生了与射流方向相反的流动．随着时间的推移，射流流体逐渐上升并向自由表面聚集，从图5(c)及后续的各图可以看出，射流流体在运动到自由表面之后会将一部分能量传递给自由表面，从而引起自由表面流体的向前流动，同时还会有一部分射流在自由表面的作用下发生反射，形成斜向下的流动．从图中还可以看出，随着流体不断向自由表面聚集并反射，这种斜向下的流动结构也逐渐增大，同时在背景流体粘性作用下也会继续向其上下两侧发展，并形成局部微小的涡结构．

图6给出了背景流场中纵剖面上与上述速度矢量场相对应时刻的涡量场分布．从图中可以看出，各个时刻的涡量场均呈符号相反的块状分布，说明流场的中纵剖面上有许多局部微小的涡结构产生．

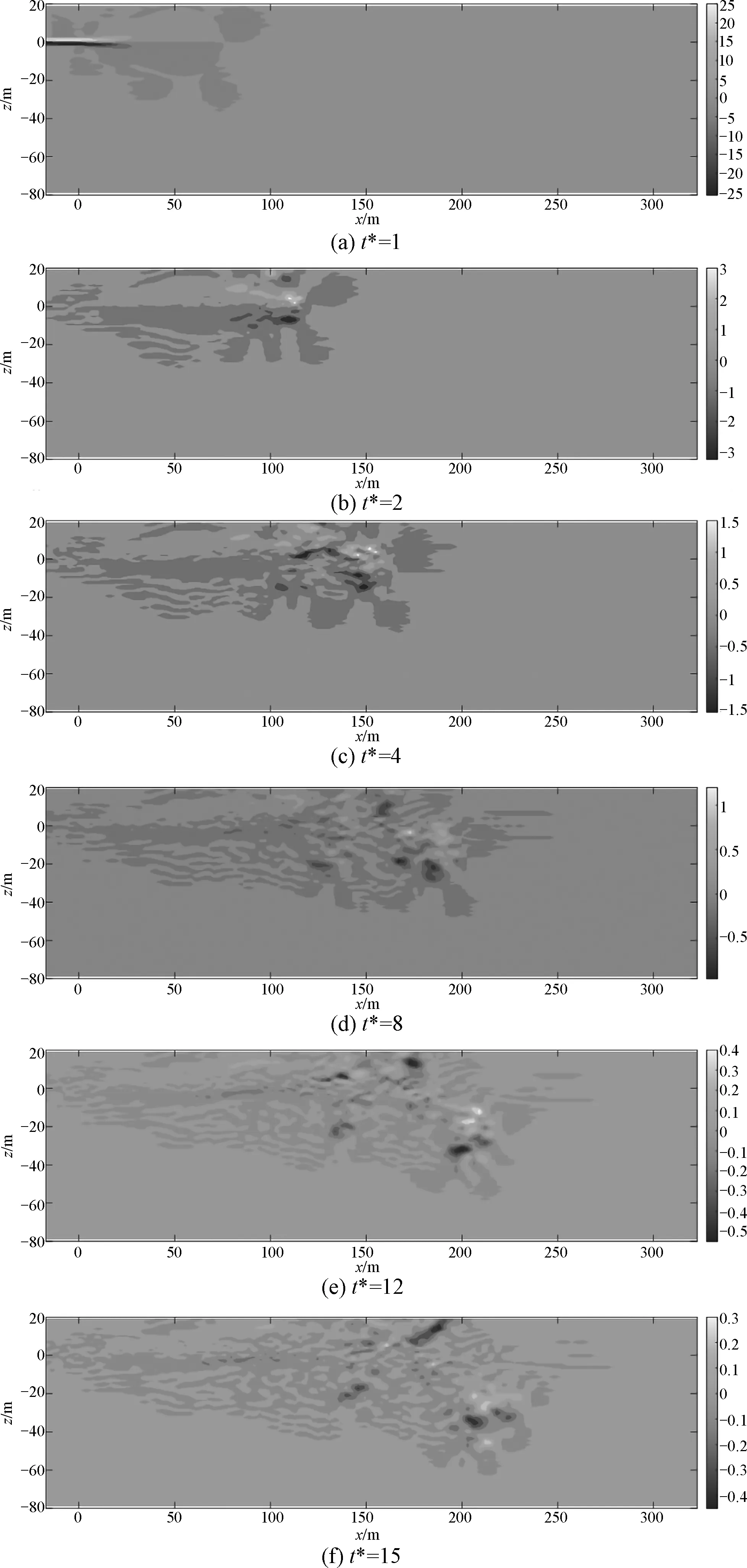
图6 中纵剖面上6个不同时刻的涡量分布(s-1)Fig.6 Vorticity distribution (s-1) on the middle longitudinal profile at six different moments

其中，图6(a)中的涡量场在射流圆管中轴线两侧呈对称分布，表明涡结构具有一定的对称性，这是由于此刻的射流还没有受到自由表面的影响，涡量保持在较高的极值．从图6(b)开始射流逐渐受到自由表面的影响，垂向方向上的自由表面附近有涡结构生成，同时图6(a、b、c、d)中涡量的极值和图6(a)相比迅速减小了一个数量级．在图6(e、f)中，中纵剖面上有更多的局部涡结构生成，且分布更加广泛，同时涡量的极值接着又减小了一个数量级．

2.3 自由表面流场的变化特征

图7为背景流场自由表面上不同时刻的速度矢量图．从图中可以明显地看出，图示各个时刻下的自由表面上均有流体运动产生，而且自由表面上的流体会向着包括与射流方向相反的方向等四面八方流动，就好像水面以下有一股流体向自由表面涌出一样．同时，图示的自由表面速度场呈现出了两种截然不同的流动形态，在图7(a～g)中，流动速度表现出从自由表面上的某一点发出然后汇聚到自由表面上另一点的特征，这和经典流体力学中理想状态下的“源”、“汇”流子的流态相似，这种流动形态和[14]的实验研究中初始扰动阶段时自由表面上的速度场相似，并且这种流动形态随着时间的发展逐渐向前推移，在图7(a～e)中这种流动结构的大小范围变化不是特别明显，但到了图7(f～g)中这种流动结构的大小范围迅速减小，并进而转变为了图7(h～l)中的另外一种流动形态，其流动速度表现为从自由表面上的某一点向外发出，而不向某一点汇合，这种流动形态也随着时间的推移而逐渐向前移动，并且向射流反方向运动的流体逐渐减少，反而向着射流方向运动的流体越来越多，这是因为自由表面受到向前流动射流的影响越来越显著，同时这种流动结构的大小范围逐渐变大．另外，这种流动形态的自由表面上向前流动的流体在周围流体粘性剪切作用的影响下，流速会向前方的左右两侧偏转，进而形成局部微小的涡结构，这一点也可以从后文的涡量分布图中得到验证．在的实验研究中这一阶段属于涡演化阶段，有一对旋转方向相反的涡对形成，但是本数值试验研究中这一现象不明显，可能是经过时间的发展流体的动能耗散的较快．

图8给出了与图7中同时刻的涡量分布图．由图可知，在图8(a～e)中，各个时刻下自由表面上的涡量主要聚集在自由表面左侧边界处的较小范围内，并关于中纵剖线呈对称分布，但是这些涡量的值却很小，甚至可以忽略不计，图8(a～e)中的射流主流动对自由表面的影响区域内却没有涡

量(或涡量接近于零)，说明这些时刻下自由表面上的主流动区域内并没有涡结构产生；在图8(f～l)中，各个时刻下自由表面上的涡量均位于主流动区域内并呈符号相反的块状分布，说明这些时刻下自由表面上确实有涡结构产生，同时各个时刻下自由表面上的涡量分布大致关于中纵剖线对称，说明涡结构大致关于中纵剖线对称．另外，随着时间的增加，块状结构的分布范围逐渐扩大，说明涡结构的分布范围在逐渐扩大．从图8(f～l)中还可以看出，除了图8(f)之外的其余各个时刻下自由表面上涡量的极值大致相等．

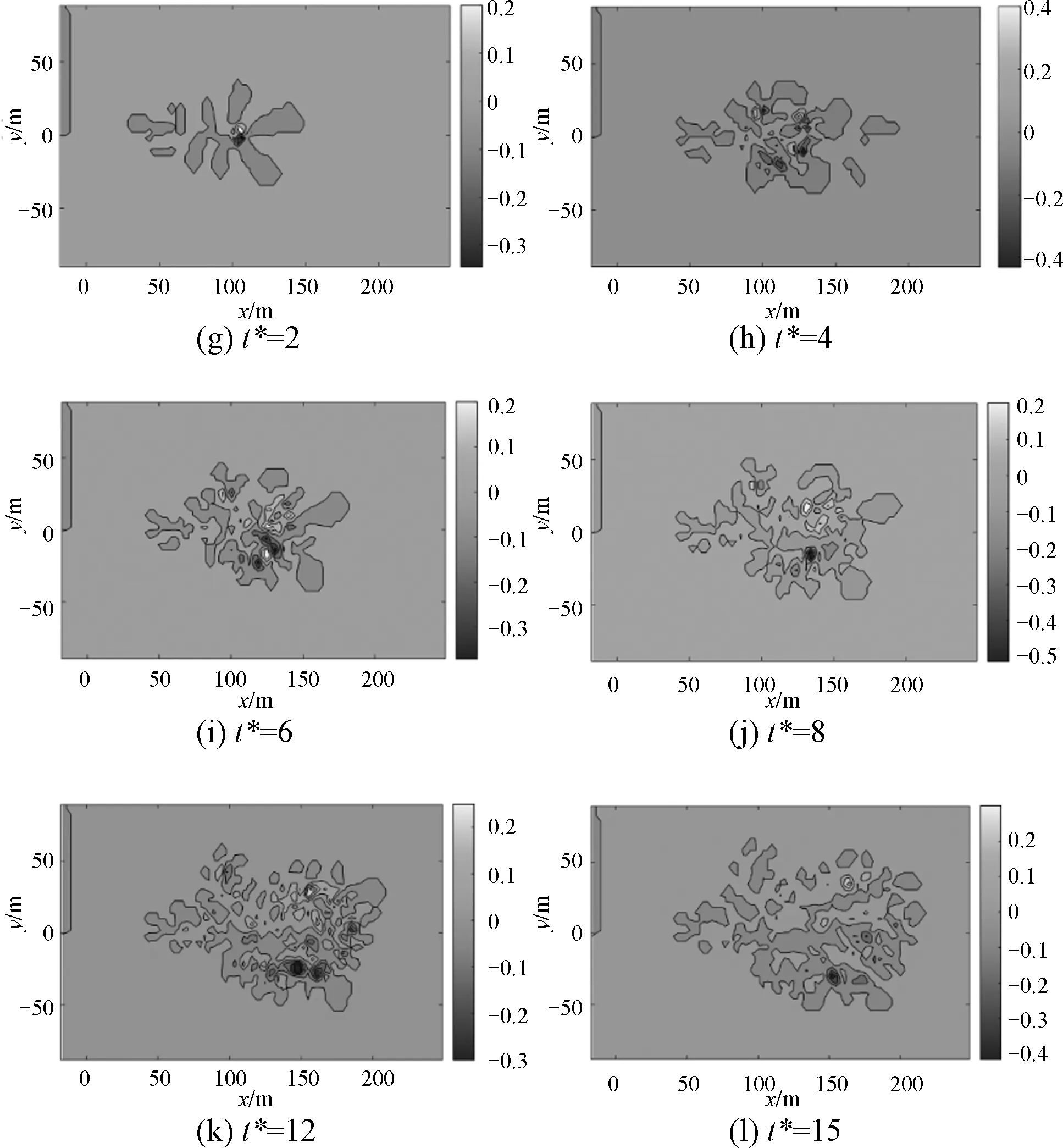
图8 自由表面上不同时刻时的涡量分布图(s-1)Fig.8 Vorticity distribution(s-1) on the free surface at different moments

图9给出了自由表面上的无量纲动能Ef*和无量纲动量Pf*随无量纲时间t*的变化曲线．从图中可以看出，自由表面上的动能总体上随着时间的增加从零开始逐渐增大，这是因为自由表面上的流体逐渐受到了来自水下湍流潜射流的能量供给，即射流将一部分能量传输到了自由表面上．同时，也可以看到中间有一个时间段，自由表面上的动能经历了小幅下降后又逐渐上升的过程，这是因为在这一时间段，自由表面上与射流方向速度相反的流动逐渐减少，导致动能有所下降，接着与射流方向速度相同的流动逐渐增多，导致动能又逐渐增大．另外，从图中动能变化的梯度来看，刚开始动能随时间增加的很快，后面慢慢接近于某一常值，说明自由表面上流体的流动状态逐渐趋于平稳．从自由表面上动量的变化来看，总体上也是随着时间从零开始逐渐增大，并且在某些时间段上动量也经历了先下降后上升的变化过程，这和自由表面上流体流动速度的大小和方向的变化有关，最终动量的变化趋势也逐渐趋于平缓．

图9 自由表面上的无量纲动能Ef*和无量 纲动量Pf*随无量纲时间t*的演化规律Fig.9 Evolution of dimensionless kinetic energy and dimensionless momentum with dimensionless time t* on the free surface

3 结论

(1) 在射流刚结束时，湍流涡结构保持着完整的球形冠状结构，随着时间的推移，涡结构的横向尺度逐渐扩大，并在自由表面上形成若干涡对结构，表现出准二维的流动特征，涡的前端出现明显的塌陷现象，并有逐步脱离涡结构主体的趋势，同时涡结构从某一时刻开始达到某种相对稳定的结构．

(2) 从中纵剖面上垂向的速度场与涡量场的变化特征来看，射流刚结束时，流动还没有受到自由表面的影响，速度矢量场呈现出对称的分布，并在上下方向上扩散，涡量场也关于圆管中轴线对称．伴随时间的变化，射流流动受到水面的影响，自由表面产生了与射流方向相反的流动，射流流体逐渐上升并向自由表面聚集，同时还会有一部分射流在自由表面的作用下发生反射，形成斜向下的流动，同时中纵剖面上形成了许多局部微小的涡结构．

(3) 在对自由表面上的流场特征进行研究发现，自由表面上的速度场呈现出两种截然不同的流动形态，随着时间的发展由一种类似“源”“汇”组成的流动形态逐渐转变为一种速度从某一点发出而不向某一点汇合并随时间逐渐向前发展的流动形态．涡量图显示了自由表面上从某一时刻开始有许多局部微小的涡结构形成，同时各个时刻下自由表面上的涡量分布大致关于中纵剖线对称，说明涡结构大致关于中纵剖线对称．另外，随着时间的增加，块状结构的分布范围逐渐扩大，说明涡结构的分布范围在逐渐扩大．