基于多目标优化的蛋白质三维结构预测
2021-10-19王雨林沈红斌
王雨林,张 彪,沈红斌
(上海交通大学 图像处理与模式识别研究所, 上海 200240)
蛋白质在生命细胞中发挥着各种各样的功能,是生命活动的主要承担者之一[1-2].自然界的蛋白质主要由20种基本氨基酸构成,存在着一条或多条肽链,长度从几十到几千不等.蛋白质的结构基本决定了其特别的生物化学特性,自20世纪50年代起围绕求解蛋白质三维结构的研究获得了广泛的关注[3-5].但由于实验的困难性[6],从蛋白质序列出发利用计算机算法预测每个氨基酸的空间坐标并进而最终实现三维结构的预测获得广泛重视.总体而言,当前基于氨基酸序列来预测蛋白质结构的方法大致分为3类[7-8]:同源性建模法、穿线法以及从头预测法.
同源建模法是一种十分成功的蛋白质结构预测方法,其基本的假设是结构的变化率远低于序列的变化率,氨基酸序列包含了预测蛋白质结构的充足信息[9].基于以上思想,同源建模法通过比对序列与PDB(protein data bank)数据库中已经实验求解获得结构的模板蛋白质序列的相似性[10-13],当相似性高于一定的阈值时,说明它们可能具有相似的空间结构,并用模板的结构作为待预测的结构基础,在施加部分相关约束的同时优化缺失的重原子与支链,最终优化获得预测目标结构.当能找到高可靠模板时,这类同源建模法能取得很高的准确性,但当无法寻找到同源性蛋白时,此方法难以取得好的效果.
穿线法在两个蛋白质即使序列相似性很低,也可能具有相同的结构方面取得了较大的研究进展[14].自然界中存在着数量很大的氨基酸序列,但是它们对应的不同三维结构却比较有限.在进行蛋白质结构预测时,相比于直接进行序列与序列的比对,序列与三维结构的比对往往能取得更好的效果[15].穿线法大致可以分为两类[16-18]:一类提取蛋白质的特征,如蛋白质的二级结构、氨基酸残基的可溶性等,来构建特征向量作为蛋白质的特征表示,然后用动态规划等相似算法将序列与当前的特征进行比对得到序列对应的三维结构;另一类方法基于统计势能的方式,如统计在特定距离上两个氨基酸残基对出现的频率,来评估序列与蛋白质结构的相似性,从而预测获得三维结构.
尽管基于同源建模法与穿线法的蛋白质三维结构预测取得了很大的成功,但是仍然有许多重要的蛋白质因为无法找到合适的模板结构而难以取得好的效果,此时需要采取从头预测法的方法.基于从头预测法的研究一般分为两类[19]:① 通过模拟蛋白质的折叠过程,从随机构象出发优化预先给定的能量函数至最低状态;② 基于碎片组装的方式进行结构预测[20].两种方法的的核心都在于获得能准确评估结构的能量函数[21]和高效的构象空间搜索方法.第一类方法目前广泛采用分子动力学模拟的方式,通过解析天然蛋白质折叠时的机理与相互作用来指导预测序列的折叠与构象生成.然而一方面模拟蛋白质折叠的过程十分耗时[22],并且即使投入大量的算力,对长度较长的蛋白也难以达到高的精确度;另一方面,实验模拟蛋白质折叠的过程本身与自然界的天然折叠方式存在偏差,生成的结构与天然结构可能会有诸多不同.
为了解决上述问题,以ROSETTA[23]为代表的第二类方法通过引入构象的约束来减少计算的复杂性.ROSETTA基于以下一个重要假设[23]:短序列片段具有很强的局部结构偏好,并且这种偏好的强度与多样性高度依赖于序列本身.ROSETTA首先计算序列的二级结构,蛋白质的二级结构整体规划了多肽链沿主链骨架方向的空间排列和走向;然后以二级结构为约束条件,将序列以滑动窗口的方式与蛋白质数据库中的结构进行相似性比对,数据库中的结构具有坐标信息,与序列有高相似度的结构坐标可以转化后作为序列的坐标.算法通过生成具有坐标的碎片的方式,随机在序列上选取位点替换为备选的碎片结构,来改善构象的结构,并使用单个能量函数进行评估,朝全局自由能降低的方向优化构象,最终得到能量最低的结构.ROSETTA 算法取得了很好的效果[23],但是在部分蛋白的预测上不能找到全局最优解,其中一个重要的潜在原因是仅使用单个能量函数进行优化.由于能量函数并非完全精确,对构象的评价和构象本身与天然结构的相似度不是完全的正相关,在优化过程中存在着舍弃掉最优解的情况.
正是考虑到很难用统一的单能量函数衡量所有构象的质量,文中采用多个能量函数优化构象的TRIOFOLD 方法,多个能量函数的引入能进一步扩大搜索空间,对于构象的评价将更加全面,能帮助优化搜索的方向,也有助于克服能量函数本身的精度问题.实验结果验证了TRIOFOLD方法的可行性,该方法有望成为领域已有算法的有益补充.
1 TRIOFOLD多目标优化算法
文中采用从头预测法的方法,通过碎片替换的方式对生成的构象进行更新,并利用多目标优化的方法对生成的构象进行优化,最终在迭代终止时生成蛋白质结构的非支配集合,算法流程如图1.
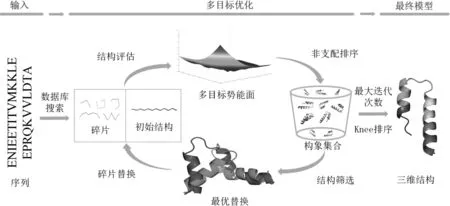
图1 TRIOFOLD多目标优化算法流程Fig.1 Flowchart of TRIOFOLD multi-objective optimization algorithm
1.1 能量函数
预测过程中,蛋白质可以通过能量函数得到一个表征自身结构质量的数值,分别引入3个能量函数ROSETTA、CHARMM[24]、RWPLUS[25]对程序生成的临时构象进行评价筛选.CHARMM是基于物理学意义的能量函数,其定义了一套广泛应用于分子动力学的力场,可以对蛋白质结构的键长、键角、原子之间的相互作用等进行定量化计算,得到一系列的数值来评估蛋白质结构的真实性;RWPLUS是基于统计学意义的能量函数,其使用随机游走链作为参考状态对蛋白质结构进行评价;ROSETTA是以上两种类型的综合,它的一部分能量项计算力的作用,另一部分能量项基于统计得到,最后将所有能量项数值加权求和作为蛋白质评估的分数.
1.2 基于单目标函数的构象优化
ROSETTA算法首先计算序列的二级结构信息和序列与蛋白质数据库中数据的相似信息作为约束,在已知结构的序列碎片数据库中为序列的所有子序列选定具有高相似性的短碎片结构.然后根据序列信息生成初始构象,选取长度固定的滑动窗口随机在序列上选择一个局部子序列,使用当前子序列的备选碎片结构替换原始结构,生成新的临时构象.在模拟退火算法下,使用ROSETTA的能量函数对构象进行评估,基于Metropolis准则[26]决定临时构象的保留或是舍弃.不断迭代以上过程,直到达到规定的接受次数,输出最终的结构.
具体而言,对于新生成的构象采用单能量函数进行评估,比较当前构象与上一次构象的能量函数值,计算出新构象的可行性概率,按一定概率接受新的构象:
(1)
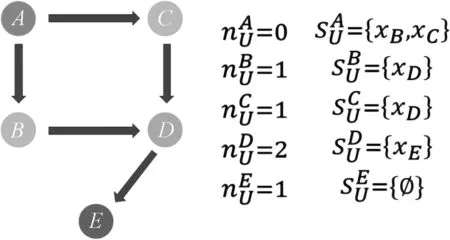
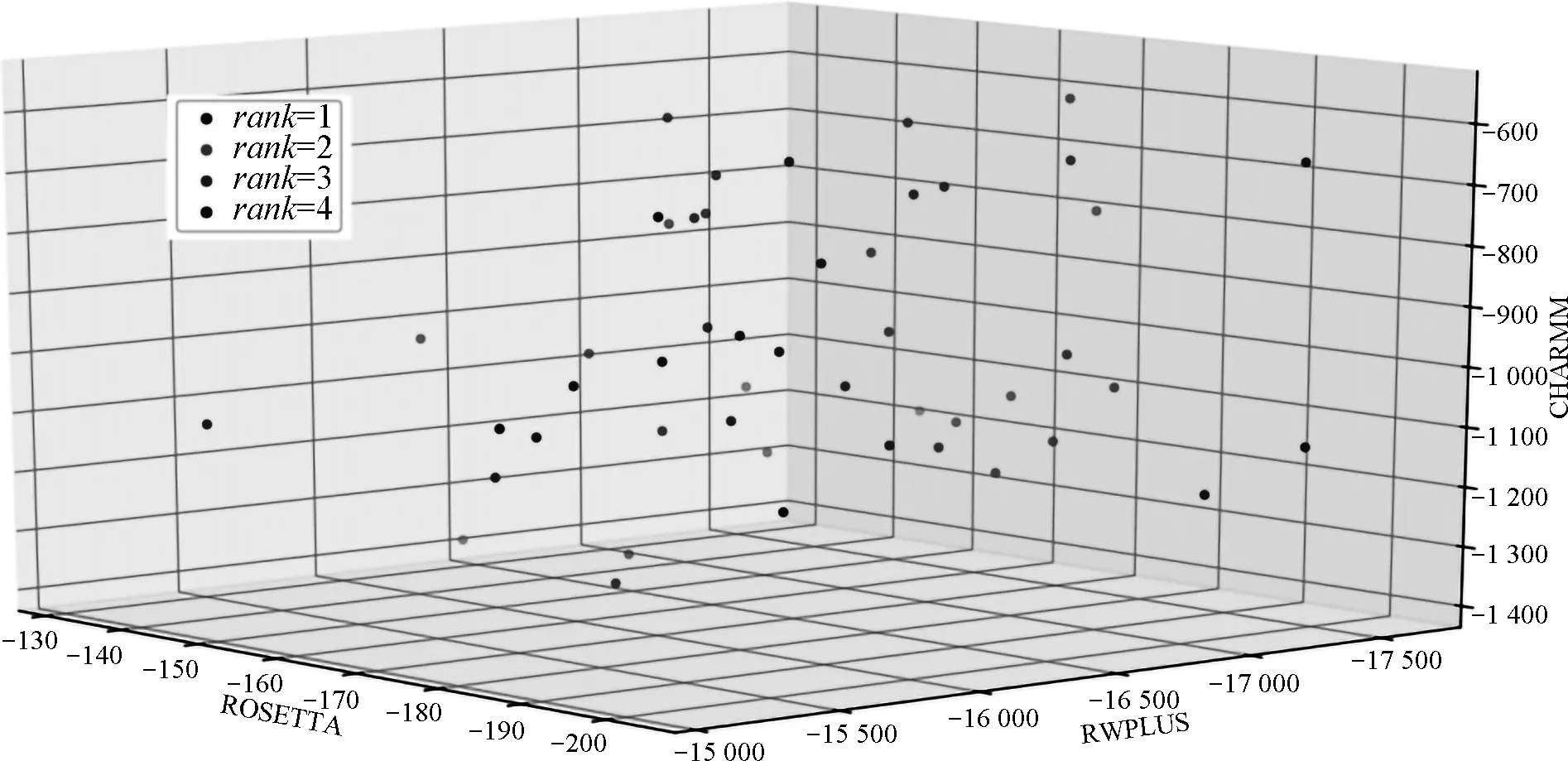
式中:x(n)为当前构象;x(n+1)为生成的新构象;E(n)和E(n+1)分别为对应的能量评估;参数T为控制模拟退火快慢的调节因子.若当前构象的能量小于上一步构象的能量,当前的替换操作将会被接受;若当前构象的能量大于上一步构象的能量,算法将产生一个在区间[0,1]的随机数ε,对于式(1)计算的概率p,如果ε ROSETTA的重点之一是最小化序列中残基局部和全局的交互作用来优化生成的构象结构,使用单个能量函数作为约束提高搜索效率,通过大量替换碎片结构的方式来遍历构象的解空间.但是能量函数本身是通过对自然界中的真实蛋白质采用基于统计或是基于物理力学建模的方法拟合而成,存在着误差并非完全精确.对于单个能量函数,以上的优化过程容易在单一势能方向上过度拟合,使构象陷入局部最优解中难以跳出.同时由于单一能量函数势能面狭窄,整体上生成的蛋白质相似程度很高,难以得到多样化的结构. 考虑到这个问题,领域算法常用的一个方案是采用加权求和的方式,把多个目标优化函数转换为单目标优化问题: (2) 式中:x为蛋白质的构象;f1,f2,f3为能量函数;E1,E2,E3为构象的评估能量值;α1,α2,α3为加权系数.能量函数本身是许多能量项的加权求和.但是往往权重因子α1,α2,α3难以确定,对于权重较大的能量项,其可能出现的噪声也将对整体目标函数产生很大影响.同时,利用对能量项进行线性加权的单目标优化方式,在非凸的解空间寻优问题还存在很大的挑战. 文中将多个能量作为独立的指标进行使用,实现多目标的平行优化流程框架,由于不同能量函数基于不同的原理得到,且对于蛋白质的三维结构有着各自独特的倾向性,使用多个并行能量函数同时对生成构象进行评估能够有效的缓解单个能量函数的精度问题,同时扩大了势能面,增加了解的多样性.多目标优化问题定义为: minf(x)= min[fROSETTA(x),fCHARMM(x),fRWPLUS(x)] x∈X (3) 式中:fROSETTA(x)为ROSETTA的能量函数;fCHARMM(x)为CHARMM的能量函数;fRWPLUS(x)为RWPLUS的能量函数;x为蛋白质构象;X为构象空间.多个能量函数分别作用于构象上,将涉及到处理非支配集合的生成与最优解的筛选问题. 仅使用单个能量函数对值进行比较时,简单的大小判断便能决定出优劣.但是当一个构象由多个目标函数共同评估时,将会存在支配与非支配关系[27]. 如图2,在二维空间中进行阐述.图上横纵坐标分别为两个不同的能量函数值,所有点代表解构象在能量空间中的投影.解的关系分为两类:支配与非支配.如果两个解满足 (4) 即解xA的第一个能量值与第二个能量值均比解xB对应的能量值大,则称解xB支配于解xA;如果两个解满足: (5) 即解xA的第一个能量值比解xB大,解xA的第二个能量值比解xB小,则解xA与解xB为非支配关系.图2中,解xA支配解xD、xE,解xD和解xE为非支配关系. 针对蛋白质结构的预测问题,结合非支配排序遗传算法(non-dominated sorting genetic algorithm II,NSGA-Ⅱ)[28]思想提出TRIOFOLD方法.NSGA-II算法是进化算法的一种,解决了在多个目标优化下解的排序的问题,具有较低的算法复杂度,TRIOFOLD流程如图1.算法通过大量的碎片替换迭代,尽可能多地生成不同的构象,在其中筛选出最优解.由于迭代次数庞大,传统的排序算法、整体时间复杂度很高.当前的一般多目标算法在选取非支配解时,由于只维护了非支配解,被支配的解完全被舍弃掉,使一些被支配的解无法发挥作用,从而损失了部分信息.而文中所提出的TRIOFOLD方法利用NSGA-II算法再次在被支配的解集中选取可利用的解来对其进行进一步优化并将优化后的结果重新评定,有助于从被支配的解集合中选择保留部分可靠的解.图3为多目标函数优化的流程. 图3 多目标函数优化流程Fig.3 Multi-objective function optimization process 1.4.1 非支配排序 为了从构象集合中筛选出最优构象集合,算法根据构象的多个能量函数指标进行分层筛选,分别得到不同层级非支配前沿的构象. 图4记录了每一个构象被支配数与自身支配的构象集合,每一个圆点代表一个构象,箭头代表支配关系. 图4 非支配排序示例Fig.4 Example of non-dominatedsorting 1.4.2 精英保留策略与拥挤距离 (6) 1.4.3 迭代初始解的选取 由于更新操作由单一构象进行,在多轮迭代时,需要在当前的最优构象集合P中选取用于下一轮迭代的起始构象.基于单目标能量函数构象选取的理念,首先分层计算集合P中构象的拥挤距离,选取每层具有最大拥挤距离的构象作为迭代初始构象,能够生成更多样化的结果.然后采用归一化的方式计算选取每一层的最优解的概率为: (7) 式中:j为当前层rank等级,其取值范围为rank等级分配数量;u为最大rank等级;α为rank等级对应权重.最后基于伯努利分布生成一个随机变量,选择随机变量值对应的区间构象作为下一轮的迭代初始构象.为了保证渐近收敛,算法在模拟退火的框架下进行,参数α是模拟退火温度系数T的负相关表达,随着迭代次数的增加,温度系数T越低,rank等级越高的α系数将越大,选择到的概率越低,最终的构象选取将逐渐向rank=1收敛,算法总是选择在能量函数评价下最好的构象. 在所有迭代结束后,对最终的最优解集P,选出rank=1的非支配集合输出,采用KNEE[29]算法从中挑选出最好的5个解作为最终的蛋白质预测结构. 1.4.4 算法整体流程 算法1 TRIOFOLD多目标优化流程输入:初始线性构象x'1,迭代次数s、单轮迭代碎片替换次数k;输出:第s轮迭代结束后最优构象集合Ps中rank=1的构象;1:初始化当前迭代轮数i=1,构象集合Xi、Pi-1、Pi、Ui均为空集;2:连续进行k次碎片替换操作,得到构象集合Xi={xi1,xi2,xi3,…,xik};3:合并构象集合Xi与最优构象集合Pi-1,得到临时构象集合Ui;4:按照rank等级对集合Ui进行非支配排序;5:构象按rank从小到大依次填入Pi中直至到达数量上限,记集合Ui中剩余构象最低rank等级为n;6:若n>4,舍弃Pi中所有rank>4的构象;7:若n=4,取出Pi与Ui中rank=4的所有构象,基于式(6)计算构象拥挤距离,从小到大填入Pi中,舍弃多余构象;8:基于式(6)计算出Pi中每一个rank等级的最优构象xbest;9:基于式(7)计算xbest出的选择概率Pbest,按概率选出i+1轮迭代起始构象xi+11;10:当i‱s时,i=i+1,重复步骤2~9;当i>s时,进入步骤11;11:输出最优构象集合中所有rank=1的构象. 为评估TRIOFOLD算法的效果,实验基于ROSETTA的碎片拼接框架,所有代码使用C++实现,在40个核256G内存的Linux服务器上完成实验.实验数据选取第13届蛋白质结构预测大赛(CASP13)上的10条序列作为初始的数据集,它们的序列长度小于150,更便于集中验证方法的可行性.当序列长度大于150以后,随着长度的增加,构象空间的大小将呈指数级增长,基于短碎片的方法难以在短时间内有效遍历所有的可行解. 在所提出的TRIOFOLD方法实验中,一次运行的迭代次数设置为1 250 次,每一次迭代将生成的构象集合X与上一轮构象最大数量为100的最优集合P合并,按rank顺序依次递增排序后生成新的最优集合,并挑选出最优解作为下一轮迭代初始解.单轮程序执行总计构象更新次数为250 000次.实验结果为最优集合rank=1的非支配前沿构象,考虑到计算量大且耗时,实验采用多线程计算的方式,最终的结果以每个线程的rank=1的非支配前沿构象直接相加得到. 实验结果与ROSETTA的原始方法进行比较,两种方法均基于传统的碎片拼接思想进行模拟,着重比较多个能量函数优化与单个能量函数优化间结果的差异.两种方法分别运行150次.大量的计算迭代保证了最终预测结构尽可能接近真实蛋白结构.同时相同的计算量保证算法的可比对性.由于ROSETTA仅有单个能量函数,ROSETTA方法每一轮程序计算只有1个结构生成,最终输出150个结构,TRIOFOLD 方法每一轮输出rank=1的所有结构,最后对150 轮rank=1的集合合并,计算最终的非支配解集.根据具体蛋白质的不同,最终生成的非支配解结构数量在20~60不等,并用KNEE算法进行解的排序. 表1展示了TRIOFOLD和ROSETTA在10个目标序列上的预测结果,给出了预测结构和天然结构之间的全局距离测试分数(global distance-total score,GDT-TS).GDT-TS描述了预测结构与真实结构的相近程度,值越大越接近于真实结构,选出每一个目标蛋白GDT-TS评估前5的结构作为比较.表1中可以看出TRIOFOLD整体性能优于ROSETTA,以最优结构为例,在7个蛋白质上,TRIOFOLD取得更优的结果. 表1 CASP13数据集上两种方法的预测结果 图5为蛋白质T0970进行一轮快速非支配排序后前4个rank的构象在能量空间的分布情况,非支配排序能够有效地将生成的构象进行分层,并且在空间中均匀分布. 图5 非支配排序后构象在能量空间中的分布Fig.5 Conformation distribution in energy space after non-dominated sorting 3个能量函数的优化下构象之间间距较大,体现了构象的多样化.当前迭代的构象集合将按照rank从低到高的顺序填入最优集合. 图6选取蛋白质T0970,展示了两种方法生成的最终构象集合在3个能量函数中的空间分布图,图中不同的点代表了构象在能量空间的坐标.z轴的CHARMM能量函数由于结构间差异较大,在比较时做了标准化处理,减小离群点影响的同时保证能量的相对大小关系.在相同的计算量下,TRIOFOLD方法为筛选出最优解提供的备选解集更小,更容易获得最优解.对于RWPLUS和CHARMM能量函数,ROSETTA方法未进行优化,整体的能量值相比TRIOFOLD更高,生成的结构是最优解的概率更低. 图6 TRIOFOLD和ROSETTA生成构象分布Fig.6 Conformational distribution of TRIOFOLD and ROSETTA 图7为TRIOFOLD和ROSETTA两种方法在蛋白质T0958上最好的5个模型的预测结果.图7中上方为TRIOFOLD的预测结构,下方为ROSETTA预测结构与原始结构的对比.TRIOFOLD预测结构的平均GDT-TS得分为54.16,均方根偏差(root-mean-square deviation,RMSD)为6.983,对应的ROSETTA能量为-169.ROSETTA 方法预测结构的平均GDT-TS得分为45.85,RMSD为7.301,对应的ROSETTA能量值为-179.其原因为由于不同的能量函数对不同的结构倾向性不同,多目标函数优化使得TRIOFOLD在二级结构的空间预测上更为合理,其二级结构的预测均与原始结构更加相近.ROSETTA的预测在α螺旋上存在着更大的扭转角偏差,部分结构上长度差异也较大.β折叠与无规则卷曲部分与原始结构在空间位置上有一定差异.表2为对应的统计结果,其中RMSD是用于比较两个蛋白质结构的相似度,其计算了两个蛋白质对应CA原子之间的均方根偏差.RMSD越小,代表两个蛋白质结构越相似.由表2看出,TRIOFOLD方法在GDT-TS和RMSD上均更优于ROSETTA,但是单个能量函数的能量值略微偏高,还需要进一步的优化算法. 图7 TRIOFOLD和ROSETTA的预测结构 与真实结构的比对Fig.7 Comparison of predicted structure and real structure of TRIOFOLD and ROSETTA 表2 蛋白质T0958的预测结构能量值 文中提出了基于多目标优化的TRIOFOLD方法,并通过实验验证了该方法的可行性.TRIOFOLD采用3个能量函数评估蛋白质结构,能够提供更鲁棒的优化方向.然而由于能量函数本身存在着一些误差,3个能量函数虽然能够为生成的蛋白质结构提供良好的优化方向,但是由于碎片替换的机制,对于优化的步长却很难定量的把握.这导致TRIOFOLD生成的结构能获得有效的收敛,但是与该蛋白的原始结构还是存在着一定的差距.对于一个蛋白质而言,不同的能量函数对它的灵敏度也不相同,实验中往往存在一个能量函数已经收敛而其他能量函数依旧处于可优化状态的现象,如何有效的为不同能量函数分配不同的优化方式也是待研究的问题.另外GDT-TS分数也存在着一定的与能量函数值非正相关的情况,表2中的数据有一定的体现,足够低的能量评估值仅是生成更好结构的必要条件.TRIOFOLD将直接采用GDT-TS分数作为优化指标的方式进行构象的迭代更新,将其与3个能量函数值并列加入的优化过程中,而不是仅作为最后评估的指标. 另一方面,生成整体水平更优的备选解集是下一步重要的研究方向.受限于当前算法基于碎片拼接的限制,对于一些具有很少同源结构的蛋白,TRIOFOLD难以搜索到优质的碎片结构,导致最终的解结构与真实结构相差甚远.对此,TRIOFOLD将探索加入更多的约束条件,例如序列的接触图信息等特征,为难以预测的蛋白质结构提供更多的计算信息,这样在已有的先验条件下,将缩小优化的搜索空间,并且已知的数据能够提供更高的准确性.同时TRIOFOLD也将探索采用深度学习的方式,通过统计蛋白质数据库中已有的17万个蛋白的结构特征,为序列找出更多的可行同源结构和训练出更准确的能量函数,从而优化现在的算法框架. 综上所述,文中提出的基于多目标函数并行优化的蛋白质三维结构预测方法,相对于传统的基于单目标能量函数的优化方法,TRIOFOLD充分利用了3个能量函数的势能面差异,结合进化算法NSGA-II的思想进行构象集合的迭代更新与筛选,在CASP13数据集上取得了较好的效果.是领域内已有蛋白质三维结构算法的有益补充.未来的工作将侧重于解决能量函数的精度问题和有效的组合使用问题,以及提高TRIOFOLD对于长序列蛋白和具有较低同源性蛋白的预测能力.1.3 非支配集合
1.4 基于多目标函数的构象优化

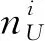
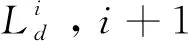



2 实验



3 结论
