月地高速再入返回器弹道重建与气动力参数辨识

李 齐，魏昊功，张正峰，陈春亮，彭 兢，杨孟飞

(1. 北京空间飞行器总体设计部，北京 100094；2. 中国空间技术研究院，北京 100094)

0 引 言

2020年12月17日，嫦娥五号返回器携带月球样品，以接近11 km/s的速度再入地球大气层，以半弹道跳跃式再入飞行后，降落在内蒙古四子王旗着陆场，圆满完成了着陆回收任务。返回器以近第二宇宙速度半弹道跳跃式再入大气层，在我国航天工程中尚属首次，与我国近地轨道再入返回器如神舟飞船和返回式卫星相比，再入过程中气动效应更为复杂，对气动数据的精准度要求更为苛刻[1]。

返回器再入弹道重建与气动力参数辨识有着非常重要的意义。通过获取真实环境下的飞行数据，利用系统辨识理论和技术，通过测量数据辨识获得真实飞行的气动力参数，对于分析高速再入弹道特性、气动特性与控制规律，验证气动设计与理论假设，验证地面试验和数值计算结果，改进气动设计方法和工具，为飞行器控制系统提供正确的气动数学模型都具有重要价值[2]。Ivchenko等[3]通过建立全局最小二乘优化问题对探空火箭碎片的GPS数据进行弹道重建。Karlgaard等[4]采用迭代广义卡尔曼滤波方法分别完成对SFDT-1和SFDT-2飞行试验器的弹道重建、大气重建和气动力重建，所获得的飞行试验数据用于系列型号研制。

月地高速再入返回器飞行测量数据具有以下特点： 1) 跳跃式再入使得飞行高度变化大，由此导致气动参数变化范围大，同时由于跳跃高度是在80 km以上的稀薄流区，气动参数不确定度大； 2) 由于高速再入大气层时形成的等离子鞘的影响，雷达测量存在黑障区，导致外测数据不完整。

对于气动力参数不确定性问题，王贵东等[5-6]利用克拉马-罗界，结合置信度得到测量噪声产生的数据偏差区间，并采用蒙特卡洛分析方法得到了时序气动参数的偏差估计。随着计算机技术不断提高，将神经网络等机器学习算法应用于气动参数辨识成为可能，但采用学习算法存在样本数量少的问题。王超等[7]采用反向传播神经网络建立了高速飞行器全弹道的非线性气动力模型，并验证建模方法的可行性。浦甲伦等[8]以神经网络为基础，利用支持向量机扩充样本，设计气动参数智能辨识方法。风洞自由飞试验同样存在数据量少的问题。对此，张天姣等[9]基于极大似然法对风洞自由飞试验开展气动参数辨识，利用有限测量数据获取飞行器的气动特性。宋威等[10]开展了大钝头返回舱跨声速风洞自由飞试验，考察动态稳定性问题，采用线性和非线性气动参数辨识获得动态和静态稳定性参数。

本文针对月地高速再入返回器跳跃式再入弹道气动参数变化范围大、气动参数不确定度大和数据不完整等特点，建立了适用于返回器外形的气动力参数模型，完成了弹道重建与气动力参数辨识，开展了不同大气模型对气动参数辨识的影响分析，完成了飞行辨识数据修正。通过与考虑复杂气动效应的地面预测气动数据对比，获得了相互校验结论。

1 弹道重建方法

返回器将内、外测数据作为输入，通过数据预处理和弹道重建，获得沿再入弹道的高度、速度、加速度、角速率、姿态角以及动压、马赫数等弹道与飞行参数。将这些输出参数再作为输入，联合大气密度模型和返回器的物理几何参数，建立运动方程组进行反解，最终获得返回器沿弹道真实飞行状态下的气动力参数和发动机开机时的力矩参数。弹道重建与气动力辨识过程的相互关系如图1所示。

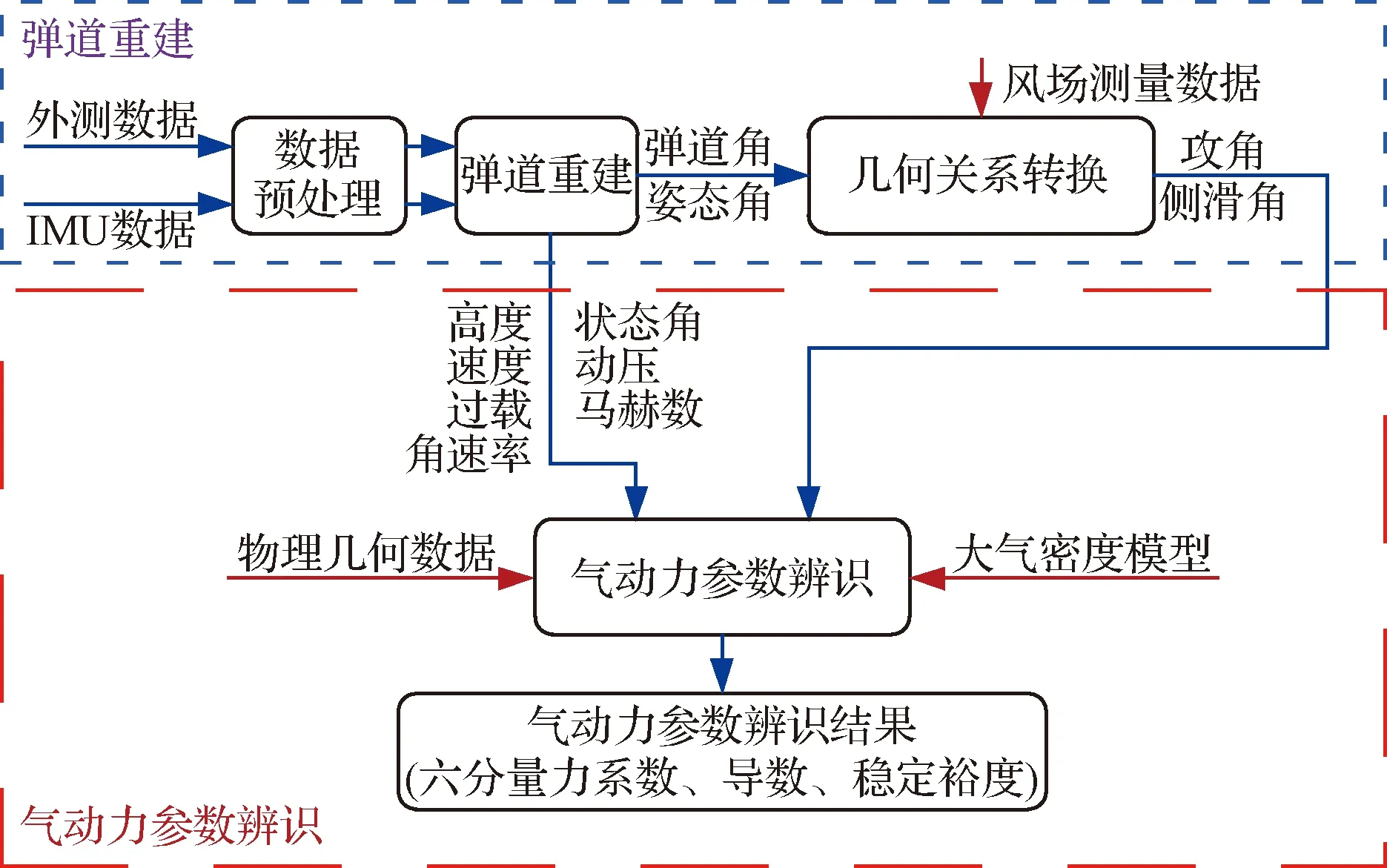
图1 弹道重建与气动力参数辨识结构框图Fig.1 Trajectory reconstruction and aerodynamic parameter identification structure

用于弹道重建和气动力参数辨识的返回器飞行数据分为内测和外测数据。其中，内测数据包括来自惯性测量单元的加速度、四元数以及来自光纤陀螺的姿态角速率；外测数据包括来自地基/船上雷达的弹道坐标、经度、纬度、高度以及来自风场探空气球的温度、气压、风速、风向等。

1.1 数据预处理

由于返回器本身及飞行环境条件的复杂性，传感器和数据采集系统非理想性等众多因素的影响，不可避免地使飞行实测数据中含有确定性误差和随机误差。因此在将飞行测量数据用于气动参数辨识之前，应首先对试验数据进行各种预处理，以尽可能地消除各种确定性误差和随机误差，提高气动辨识结果的准确度。具体内容包括：

1)时间的统一：将外测数据与内测数据时间原点进行统一。

2)内测四元数换算姿态角

利用内测四元数可以得到返回器在再入坐标系(或某地面固连坐标系)中的姿态角。

从再入坐标系到体轴系的转换矩阵为:

T=T3·T2·T1

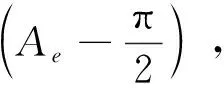
于是，返回器相对于再入坐标系中的姿态角可由下式求得：

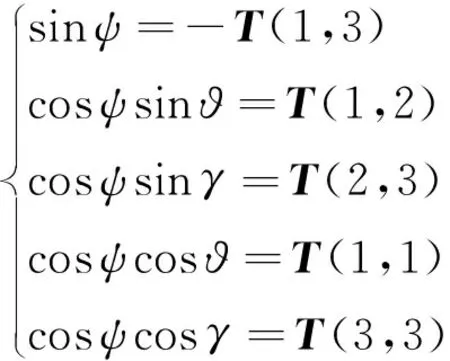
(1)

式中:γ为滚转角，ψ为偏航角，ϑ为俯仰角,T为转换矩阵。

如果把上述算法中的再入点经纬度用当地经纬度代替，得到的就是返回器的当地姿态角。

3)外测数据坐标转换及平滑

对雷达测量的矢径、仰角、方位角向再入坐标系坐标的换算，以及地心固连系中的坐标向再入坐标系坐标的换算。

4)返回器坐标系统一

通过坐标变换，返回器所受地球重力加速度在再入坐标系中的投影可表示为：

(2)

式中：gx,gy,gz为重力加速度；grωx,grωy,grωz为重力加速度径向分量;aex,aey,aez为离心加速度;acx,acy,acz为科氏加速度。

5)实测密度及风的修正

根据再入前落区附近0～25 km高度范围内的风场实测数据对辨识所采用的大气密度模型进行修正。由于实测的一般是水平风，不只是风速的大小，还有风的方向，因此需要通过姿态角把风投影到返回器体轴系中才能进行风的修正。由于再入坐标系原点与落区相差往往超过20°的地心角，因此进行风的修正时必须考虑地球的曲率，即考虑再入点与落区的经纬度差别。

6)跳点的识别、剔除与补正

飞行中外界干扰或仪器偶然跳动，可能使测量结果出现跳点。如何准确区分跳点与数据分散度，需要建立正确的判据。通常跳点剔除所采用的判据，如Chauvenet[11]、Grubbs[12]等提出的判据，无法直接用于气动参数辨识所用的角速率、过载这类振荡型试验数据；基于状态方程采用卡尔曼滤波、分割辨识算法或最大似然法也可用于识别和剔除跳点，但对数据预处理来说过于复杂。本文采用简单的滑弧算法。

7)数据平滑

数据预处理的另一项重要工作就是采用数据平滑器将高频噪声去除，留下气动参数辨识所需的低频信息。工程上常采用的平滑算法很多，如多项式平滑、样条函数平滑、最优Fourier平滑等。本文研究采用了多项式平滑方法。

8)时间延迟修正

滤波器时间延迟、采样时刻差异及传导时刻差，通常在测量系统设计时就是已知的，只需用下式进行修正：

z(t)=zm(t+Δt)

(3)

式中:z是测量向量,下标m表示测量结果。

传感器对外作用的动态响应的时间延迟也能够以一个常值时间延迟Δt来近似。

9)传感器安装位置校正

陀螺对返回器姿态角速率的测量值与它在飞行器上的安装位置无关，但加速度的测量值与其安装位置有关，传感器不仅感受质心处的值，同时还感受由角速率引起的附加值。因此，在对加速度数据进行预处理时，应将实测值换算成质心处的值。

1.2 弹道重建算法

输出误差模型的一般形式为：

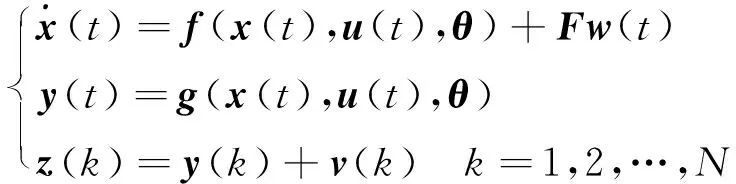
(4)

式中:x∈Rn,u∈Rr,y∈Rm分别是状态向量、输入向量、观测向量；θ∈Rp为待辨识参数向量；z∈Rm是测量向量；N是采样数据长度；f,g分别是相应维的非线性实值函数；F是时不变过程噪声矩阵；w(t)与v(k)分别是过程噪声和观测噪声，假定为独立无关的零均值高斯白噪声，则极大似然估计的指标函数为:

(5)

式中:v(k)为输出误差。

(6)

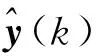
(7)

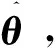
(8)

式中:

(9)

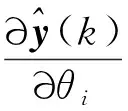
迭代求解的一般过程：首先给定辨识参数初值及状态初值，根据式(1)的状态方程及观测方程计算状态变量及观测量，同时计算输出误差；然后根据式(7)计算协方差矩阵R；通过求解灵敏度方程计算灵敏度矩阵，代入式(8)进行辨识参数更新，反复迭代直至最终收敛。

式(4)中状态方程的具体形式为:

(10)

其中:

(11)

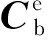
θ=(Δp,ΔV,Δq,Δa,Δω)

(12)

式(4)中第三行测量方程的具体形式为:

(13)

式中:下标m表示测量结果，εi(i=1,2,3)为高斯白噪声。

2 攻角和侧滑角计算方法

基于重建后的弹道数据计算攻角和侧滑角。由于在较低高度下的飞行速度较低，风对飞行器攻角和侧滑角影响较大，因此必须考虑风速的影响。体轴系速度:

(14)

(15)

式中:α为攻角，β为侧滑角，V为合速度。

3 气动力参数辨识方法

3.1 线性回归法

将系统模型方程以及回归方程推广为包含多个变量的情形：

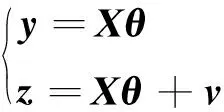
(16)

式中:z=[z(1),z(2), …,z(N)]T为N×1维测量向量；θ=[θ0,θ1,θ2, …,θn]T为np×1维未知参数向量，np=n+1；X=[1,ξ1, …,ξn]由回归量构成N×np维向量，回归量ξj，j=1, 2, …,n是由参数构成的函数；v=[v(1),v(2), …,v(N)]T由测量误差构成的N×1维向量，随机误差项vm包含未知参数扰动量以及因变量的随机测量误差。

方程误差辨识模型中，误差项可假定具有以下性质：

E(vvT)=σ2I

(17)

给定z，参数θ的最佳估计值来自于最小化测量输出和模型输出的方差和，即方程误差辨识的目标函数为：

(18)

极小化J(θ)，得：

(19)

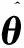
(20)

其中:np×np维矩阵XTX是对称矩阵。

3.2 气动力模型

对于气动参数辨识，无量纲的气动力系数属于因变量。通过最小化每一个运动方程的误差方差和，可以得到相应的气动力系数。气动力系数值无法通过飞行直接测量，必须通过其它测量值和运动方程解算。方程简化为：

(21)

(22)

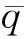
回归量一般由飞行器状态变量和控制变量的直接测量值解算得到。回归量基于经验给出备选集合，再从备选回归量集中选择与输出量相关性高的项。气动力初始模型如下：

(23)

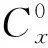
4 辨识结果

4.1 弹道重建结果

重建弹道与外测数据对比如图2所示。本次飞行内测数据与外测数据一致性较好，最大偏差出现在第一次再入跳出点附近，最大高度偏差约为1.8 km。经过弹道重建修正后，重建弹道数据与外测数据最大高度偏差均小于1 km。弹道重建结果见表1。

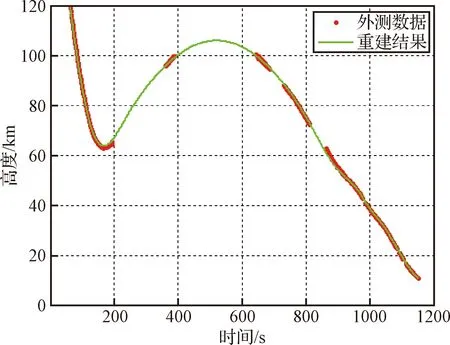
图2 重建弹道高度Fig.2 Reconstructed flight altitude

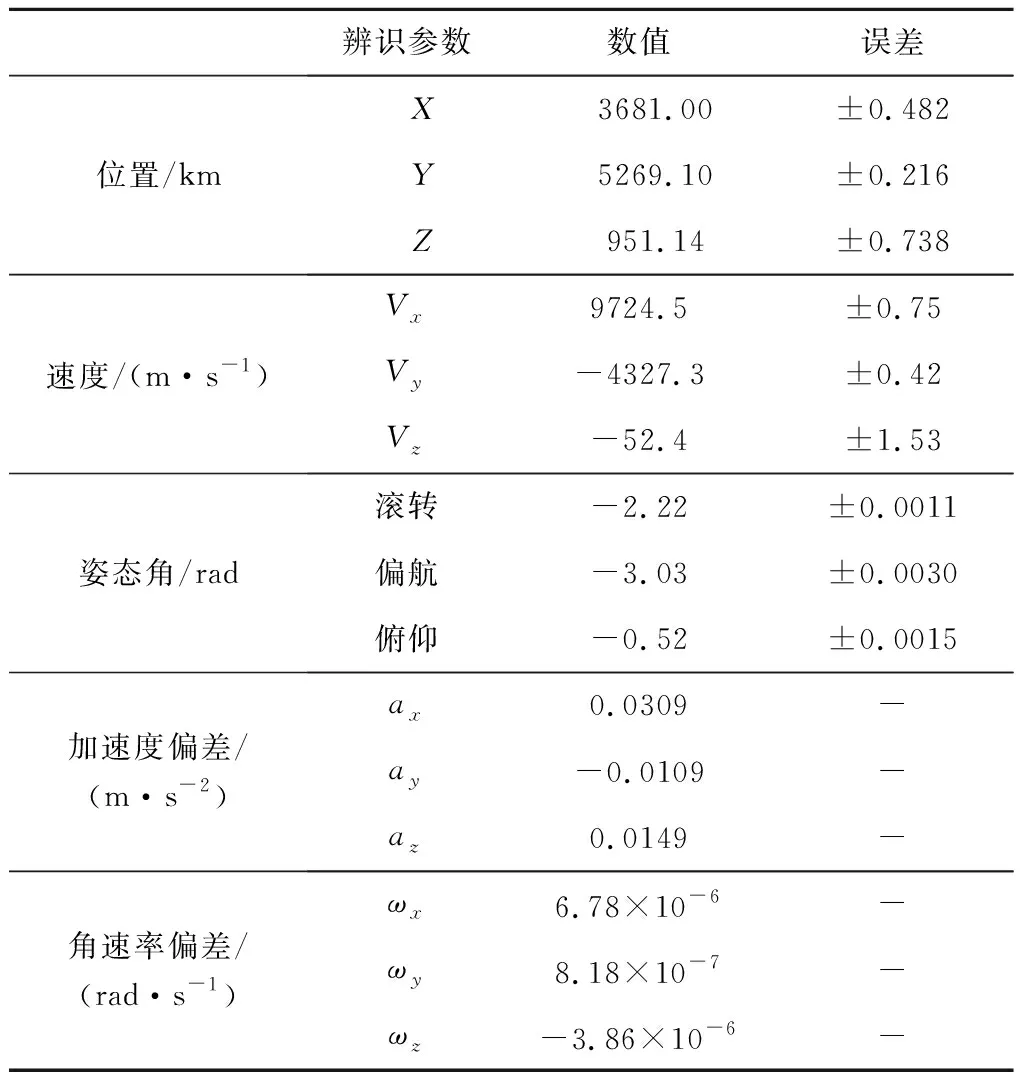
表1 弹道重建结果Table 1 Trajectory reconstruction results

4.2 攻角与侧滑角辨识结果

采用着陆区风场数据修正前后返回器再入飞行攻角随再入时间的变化曲线如图3所示。由图可见，大部分时间攻角变化平缓，振幅较小；当高度小于25 km后，返回器飞行稳定性减弱，姿态振荡增大。经过着陆场风修正后，25 km以下攻角变化规律与修正前相反，表征了返回器亚跨声速段风对姿态的影响十分显著。

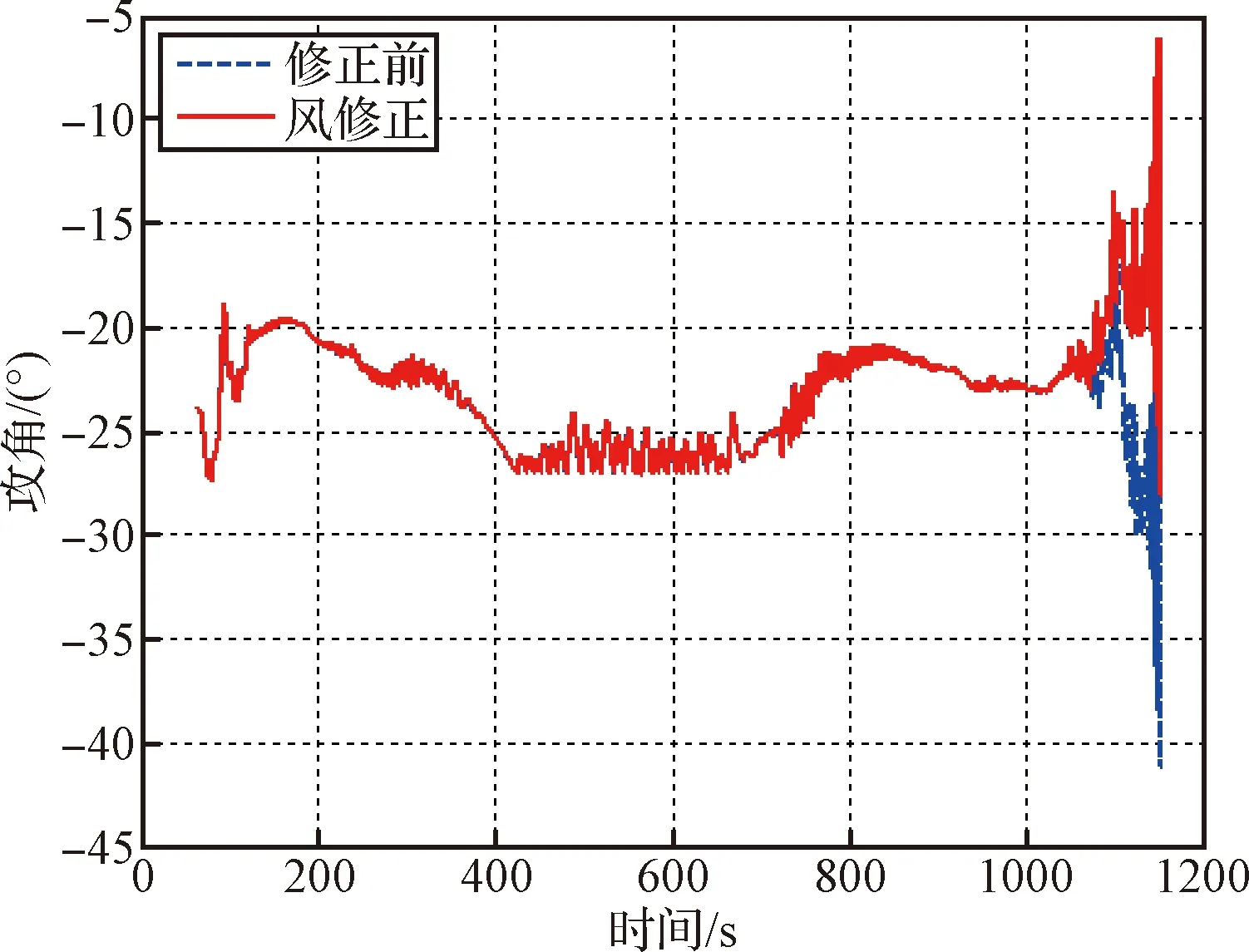
图3 飞行攻角辨识值沿弹道变化Fig.3 Reconstructed angle of attack

采用着陆区风场数据修正前后返回器侧滑角沿弹道的变化曲线如图4所示。由图可见，飞行侧滑角基本在0°附近振荡。其中，30～80 km侧滑角基本在±2°范围内变化。30 km以下和80 km以上侧滑角振荡较大，这主要是由于返回器在亚跨声速范围动不稳定和高空动稳定性减弱所致。风修正后，侧滑角均值随高度和速度的降低逐渐增大。

图4 飞行侧滑角辨识值沿弹道变化Fig.4 Reconstructed sideslip angle

4.3 气动力参数辨识结果

基于辨识算法，首先采用美国1976大气模型辨识出气动升力系数和气动阻力系数。图5为升力系数、阻力系数和升阻比沿弹道变化。通过与地面设计配平值对比可知，辨识得到的升力系数在高度30 km以上低于地面设计值，辨识得到的阻力系数在高度30～90 km之间低于地面设计值，结合升力系数对比结果，可推测辨识采用的大气密度值高于实际飞行时同高度大气密度。由于中高空大气模型对气动力参数(升力系数和阻力系数)辨识结果影响很大，为获得更为准确的辨识数据，需要开展大气模型分析，尽量减小辨识时的大气密度输入误差，此工作将在下一部分讨论。

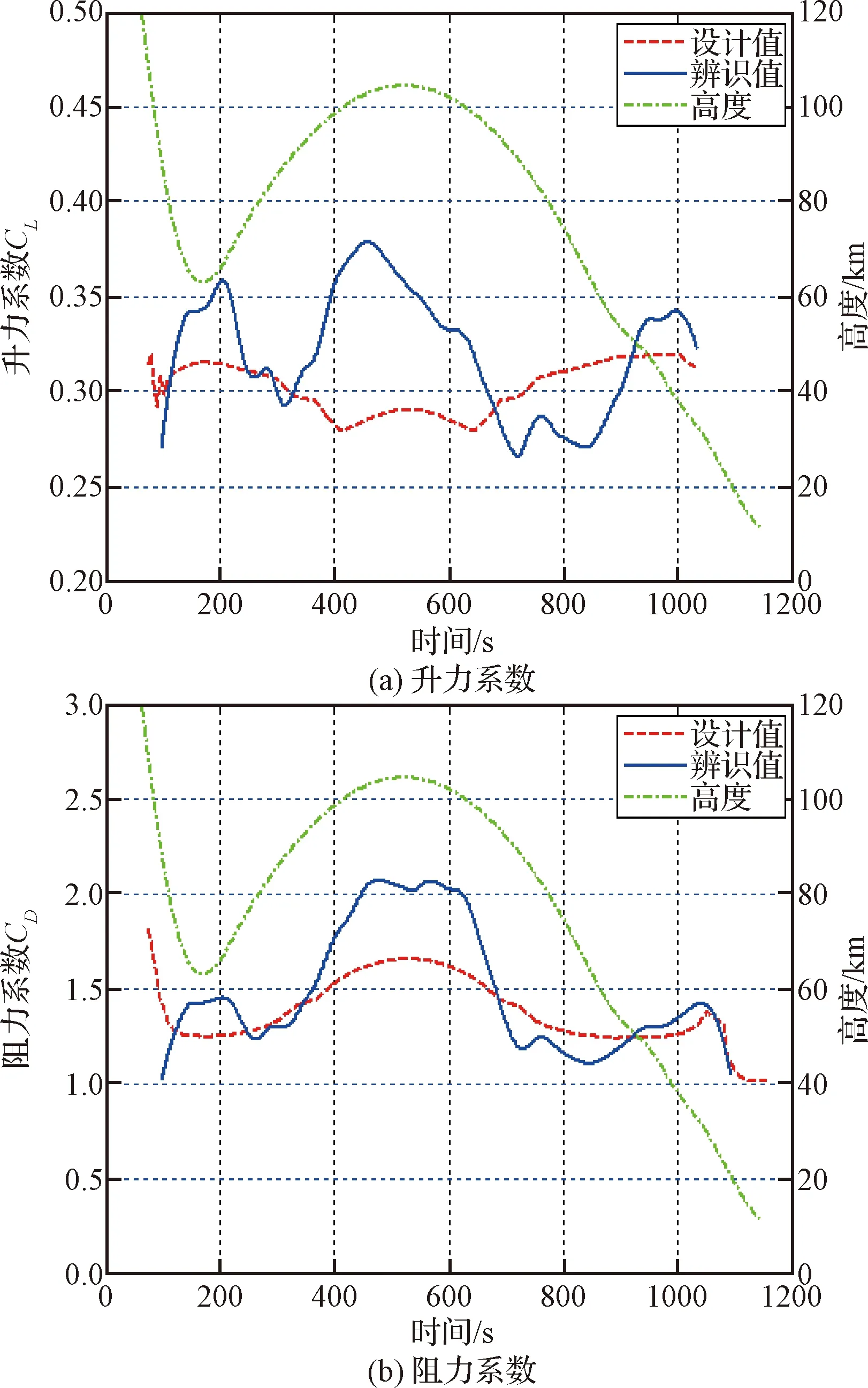
图5 升、阻力系数辨识值与地面设计值沿弹道分布对比Fig.5 Reconstructed lift, drag coefficients compared with design value

此外，由于跳出大气段传感器修正误差数值与实际加速度数值在同一量级，因此跳出大气段升阻系数辨识结果存在较大误差。因此本次90 km以上的气动力参数辨识值无法作为地面预测数据的校验依据。

为进一步分析大气模型偏差对气动力辨识的影响，本文另取两种大气模型：中国标准大气模型[13-14]以及NRLMSISE-00大气模型[15]，分别开展气动力参数辨识。图6显示了两种大气模型下轴向力系数辨识结果与美国1976大气模型辨识值在各高度下的相对偏差分布。由图6可见，60 km以上区域不同大气模型之间气动力辨识差异较大，最大可达到约35%；60 km以下美国海军大气模型与国家军用标准大气模型辨识所得气动力系数基本一致。

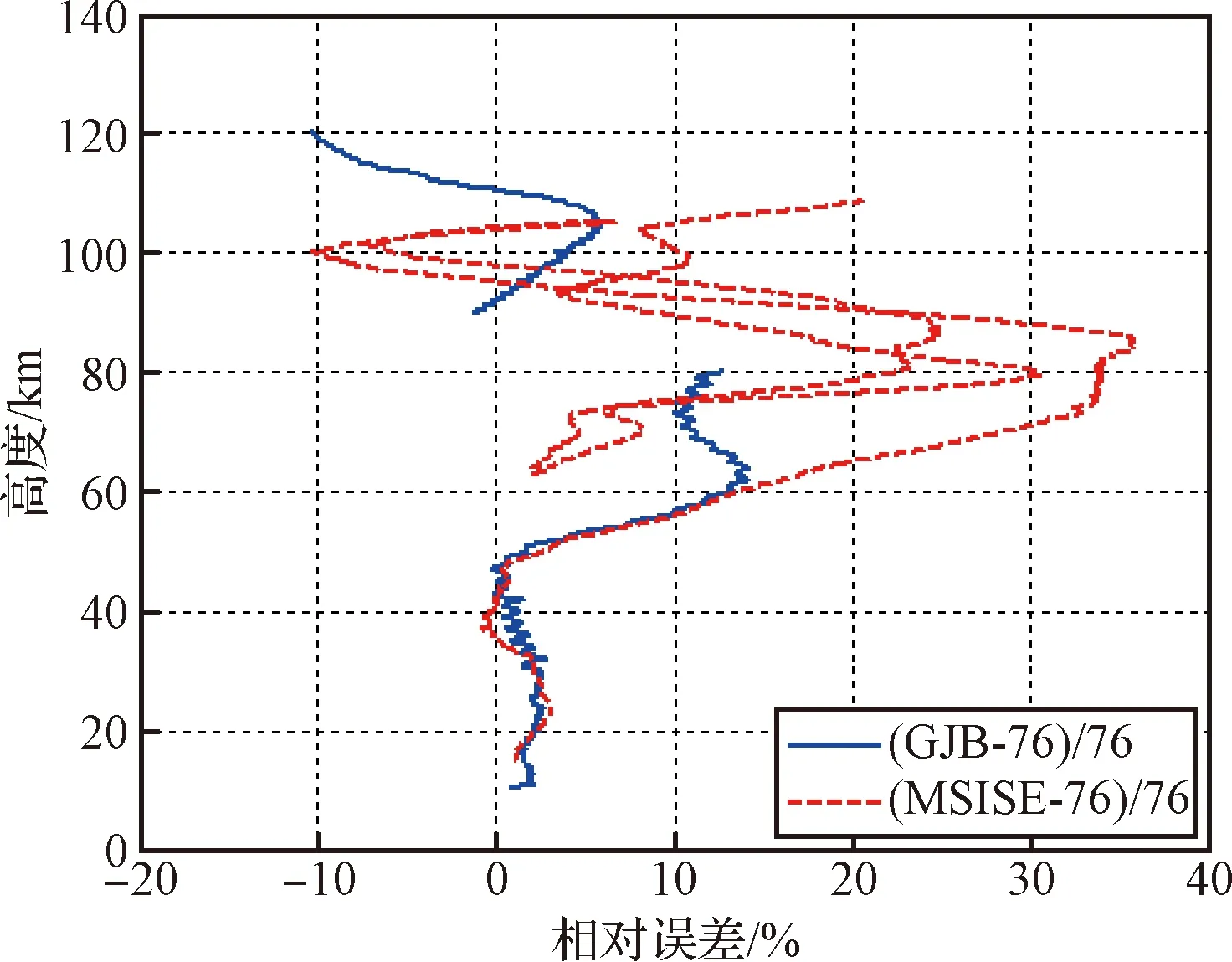
图6 不同大气模型对应轴向力系数相对偏差沿高度分布Fig.6 Deviation of axial force coefficients with respect to altitude

将辨识采用的大气密度模型按照三种大气模型的均值进行拟合后，代入返回器气动参数辨识，将所得配平攻角与配平升阻比曲线与考虑真实气体效应和烧蚀变形影响的地面预测曲线进行对比，如图7所示。由图7可见，除90 km以上的高空和30 km以下的亚跨声速段外，配平攻角与配平升阻比的辨识值与地面预测值均较为接近，同时刻同高度下配平攻角差值在1°内，配平升阻比偏差在5%以内。本次气动参数辨识数据与地面预测数据完成了相互校验。

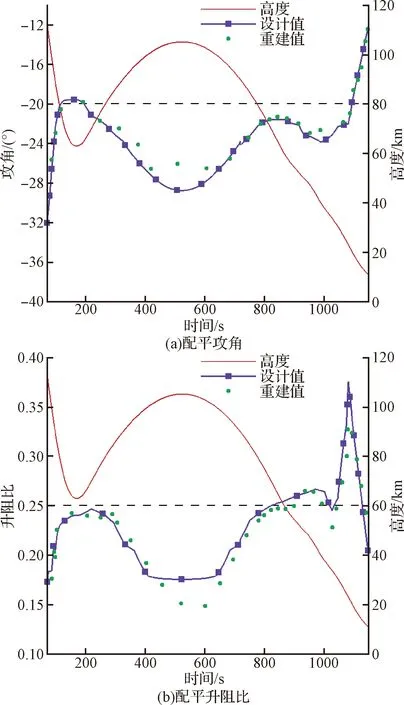
图7 配平气动特性地面预测曲线与辨识修正曲线对比Fig.7 Reconstructed trim angle of attackand lift drag ratio compared to design value

5 结 论

本文针对月地高速再入返回器跳跃式再入弹道气动参数变化范围大、气动参数不确定度大和数据不完整等特点，建立了适用于近第二宇宙速度半弹道跳跃式再入的气动力参数辨识模型，完成了弹道重建与气动力参数辨识。辨识结果表明，90 km以上高空的大气模型对辨识影响较大，除此以外，超声速和高超声速气动力辨识结果与设计值均较为接近，校验了相应速域的气动设计方法。