均匀流中悬臂圆柱体气动力雷诺数效应

王汉封+邹超+王启文+何旭辉

摘要：通过风洞试验对均匀来流中长径比为5的悬臂圆柱体气动力进行了研究.试验中圆柱直径为200 mm，来流风速为5～45 m/s，对应的雷诺数为0.68×105～6.12×105，涵盖了亚临界、临界与超临界区间.研究表明，尽管悬臂圆柱处于均匀流中，但其气动力特性在不同高度上仍存在显著的差异，悬臂圆柱气动力也存在着明显的雷诺数效应.其从亚临界进入临界区所对应的临界雷诺数略大于二维圆柱.悬臂圆柱阻力系数在临界雷诺数范围内的减小幅度明显小于二维圆柱.在亚临界区内，悬臂圆柱阻力系数小于二维圆柱的对应值，而在超临界区则大于后者.尽管处于均匀流中，悬臂圆柱不同高度所对应的临界雷诺数并不相同，越接近自由端越早出现从亚临界向临界区的转变.

关键词：钝体绕流;悬臂圆柱;气动力;雷诺数效应

中图分类号：TU317.1 文献标识码：A

Reynolds Number Effects on the Aerodynamic Forces of a

Cantilevered Circular Cylinder in Uniform Flow

WANG Han-feng1， 2， ZOU Chao1， WANG Qi-wen3， HE Xu-hui1，2

（1.School of Civil Engineering， Central South Univ， Changsha， Hunan410075，China;

2. National Laboratory for High-Speed Railway Construction， Central South Univ， Changsha， Hunan410075，China;

3. Shenzhen General Institute of Architecture Design and Research， Shenzhen， Guangdong518031， China）

Abstract： The aerodynamic forces on a cantilevered circular cylinder with an aspect ratio of 5 were experimentally investigated in a wind tunnel. The diameter of the cylinder d was 200 mm. The oncoming flow velocity ranged from 5 m/s to 45 m/s， corresponding to Reynolds number of 0.68×105 ～6.12×105， which covered subcritical， critical and transcritical regimes. It was found that， although the cantilevered cylinder is in uniform flow， its aerodynamic forces present significant differences at various spanwise positions， indicating a strong three dimensionality. Reynolds number has profound effect on the aerodynamic forces on the cantilevered cylinder. The critical Reynolds number is smaller for the cantilevered cylinder relative to that of 2D cylinder. In the critical regime， reduction in the drag coefficient （Cd） of the cantilevered cylinder is relatively smaller compared with that of 2D cylinder. In subcritical regime， Cd of the cantilevered cylinder is smaller than that of 2D cylinder. On the other hand， Cd of the former is larger in transcritical regime. The critical Reynolds number is different at various spanwise locations for the cantilevered cylinder. Transition from subcritical to critical regimes occurs earlier near the free end of the cantilevered cylinder.

Key words： flow around bluff body; cantilevered circular cylinder; aerodynamic forces; Reynolds number effects

钝体绕流问题广泛存在于土木建筑、海洋工程与交通工程等领域.流体流经钝体时，可能伴随有流动分离、再附和漩涡的脱落等复杂的流动现象.由于工程应用中的广泛需求，钝体绕流的雷诺数效应问题逐渐引起人们的重视[1].

对于正方形棱柱等带有尖锐棱角的钝体，其流动分离点固定在前缘棱角处，在不存在流动再附的情况下，雷诺数效应不显著[2].而对于圆柱等具有曲面的钝体，其气动力和尾流特性都与雷诺数密切相关.围绕二维圆柱绕流雷诺数效应已进行了大量研究[3-5].依据圆柱绕流与气动力特性，通常可将雷诺数分为4个区域，即亚临界区、临界区、超临界区与跨临界区[6].在亚临界区，圆柱表面边界层为层流分离，分离角约为80°，尾流区较宽，对应的阻力系数（Cd）约为1.2.亚临界区一直持续到Re ≈ 2×105.该临界雷诺数与很多因素有关，如：湍流度、模型表面粗糙度以及风洞阻塞度等.随着Re的增大，圆柱绕流进入临界区，某一侧边界层分离后会转变为湍流并在分离点下游某处发生再附，在圆柱表面形成一分离泡，并在下游某处再次发生分离.由于此时流动不稳定，分离泡可能只在圆柱的某一侧出现，另一侧仍为层流分离[6].临界区内圆柱两侧分离点不对称，有分离泡的一侧分离角约为140°.临界区内Cd会急剧减小，且时均升力（Cl）不为零.当Re继续增大至4×105左右时，圆柱绕流进入超临界区，圆柱两侧边界层均转变为湍流分离，分离点重新恢复为对称状态.此时分离角略为减小至120°左右，尾流区变窄，对应的Cd约为0.2～0.3.在临界区与超临界区，圆柱尾流无显著的周期性漩涡脱落.超临界区内，Cd会随Re增大而缓慢增大.至Re ≈ 5×106，Cd达到0.52左右并不再随Re变化，尾流中又重新出现较为规则的漩涡脱落，此时流动进入跨临界区[1].二维圆柱气动力雷诺数效应对干索驰振等现象有直接影响[7- 8].

目前大部分研究都是围绕二维圆柱展开的，而工程中大量存在着有限长的三维悬臂圆柱结构，如烟囱、高层建筑等[9-11].对于一端固定于壁面另一端为自由端的三维悬臂圆柱，由于受自由端后下扫流等三维流动影响，其气动力特性与尾流结构都与二维圆柱有很大差别[9].通常认为悬臂圆柱体的Cd与脉动升力系数C′l都小于二维圆柱的对应值[10-11].在亚临界区，悬臂圆柱体的Cd会随着H/d减小而逐渐减小 [12-13].当1 ≤ H/d < 6时，局部Cd最大值出现在自由端以下0.5倍圆柱直径的位置上，且小于二维圆柱Cd;而当H/d > 7时，局部Cd最大值出现在自由端处，且大于二维圆柱对应值[14].Uematsu等[15]比较了亚临界与超临界区域内H/d = 1～5圆柱的Cd的变化规律.他们发现，亚临界区内，当H/d < 5时，其对Cd的影响并不显著;而在超临界区内，对于所有H/d，Cd均减小到了亚临界对应值的43%左右.最近，Wang等[16]在亚临界与临界区内研究了H/d对悬臂圆柱体气动力的影响.发现壁面上的湍流边界层会减小悬臂圆柱体的临界雷诺数;而在均匀流中，悬臂圆柱体柱与二维圆柱临界雷诺数并无显著的区别.

Basu等[17-18]指出悬臂圆柱气动力在临界与超临界区域内的试验数据非常缺乏，这一情况至今仍然未得到彻底的改变.相对于二维圆柱，悬臂圆柱体气动力雷诺数效应的研究目前仍非常少见，相关研究大多仅集中于亚临界区.雷诺数对悬臂圆柱气动力尤其是不同高度局部气动力的影响规律目前仍不清楚.本文以长径比H/d=5的悬臂圆柱体为研究对象，通过风洞试验测量了柱体不同高度处局部气动力，系统地研究了雷诺数对悬臂圆柱体气动力的影响规律.

1试验介绍

本试验在中南大学高速铁路建造技术国家工程实验室下属高速铁路风洞内完成.该风洞为双试验段回流式风洞，其中低速试验段宽12 m，高3.5 m，长18 m，风速为2～18 m/s，湍流度小于2%;高速试验段宽3 m，高3 m，长15 m，风速为5～90 m/s，湍流度小于0.5%.本文所述全部试验均在风洞高速试验段内进行.试验模型为d = 200 mm，H/d=5的悬臂圆柱体.模型所造成的风洞阻塞度约为2.2%，其影响可忽略不计.由于圆柱迎风侧风压变化剧烈，模型表面压力测点采用了非均匀布置形式.迎风侧每5°布置一压力测点，背风侧每10°布置一个，沿圆周共计54个测点.为研究悬臂圆柱体不同

高度上的气动力特性，在底部附近，中间高度和柱体自由端附近等展向位置布置了压力测点，测点分别位于z*=1，z*= 2.5，z*= 4和z*= 4.5（本文中上标*表示用d与自由来流速度U∞无量纲化）.模型及测点布置情况如图1所示.圆柱轴线位置处风洞壁面边界层的厚度约为d，即试验中悬臂圆柱体的绝大部分都处于均匀流中，试验中还对二维圆柱风压分布进行了测量，以提供对比参照.

试验中自由来流风速U∞为5 ～ 45 m/s，对应的基于d与U∞的Re = 0.68×105 ～ 6.12×105，涵盖了亚临界、临界和超临界区域.模型表面各压力测点用内径0.6 mm的PVC测压管与压力扫描阀对应通道连接.扫描阀的采样频率为625 Hz，每通道的采样样本数20 000个.

模型表面各测压点平均压力系数Cp与脉动压力系数C′p的定义如下：

式中：P为各测点风压的平均值;P∞为风洞静压;Prms为脉动风压的均方根值.模型的时均阻力与升力系数Cd和Cl可通过平均压力系数Cp沿圆周积分获得，如式（3）所示，其中θ为测压点与模型迎风面驻点之间的顺时针方向夹角.

Cd=12∫2π0Cpcosθdθ;Cl=12∫2π0Cpsin θdθ.（3）

2结果与讨论

2.1时均阻力与升力

图2给出了H/d=5悬臂圆柱体阻力系数随雷诺数的变化规律，同时图中还给出了二维圆柱的对应结果以供对比.本试验所测二维圆柱的CdRe曲线与文献[19-20]的结果吻合很好，这验证了本试验测试方法与试验结果的可靠性.图2中二维圆柱CdRe曲线明显可分为3个区域.Re < 2×105的亚临界区，Cd≈ 1.2且基本为常数;在2×105 < Re < 4×105的临界区，Cd随Re的增大迅速减小，当Re ≈ 4×105时Cd达到最小值0.27左右，相对于亚临界区减小了约83%;在Re > 4×105的超临界区， Cd基本不再随Re变化.

与二维圆柱类似，H/d=5悬臂圆柱体的CdRe曲线同样存在类似的3个区域，但各区域对应的Re范围以及Cd值并不相同.亚临界范围内H/d=5的圆柱Cd≈ 0.85，明显小于二维圆柱对应值，这与Wang等[16]的试验结果基本吻合.这是由于悬臂圆柱自由端后下扫流会削弱展向涡脱落并显著提高柱体背压[16]，因此其Cd会明显小于二维圆柱对应值.即使当H/d=30，这一现象仍非常显著[10].

文献[16]并未给出Re > 2×105的结果，但从本试验结果可以看出，当Re = 2×105时，H/d=5的悬臂圆柱的Cd并未开始迅速减小.这说明悬臂圆柱体所对应的亚临界雷诺数范围可能比二维圆柱对应范围更大，即悬臂圆柱的临界雷诺数要大于二维圆柱对应值.从图2可以看出，当Re > 2×105时，悬臂圆柱的Cd随着Re增加开始缓慢减小.当Re = 4×105时，Cd ≈ 0.7.而当Re进一步增大时，Cd突然减小，最小至0.4左右并基本不再变化.由此可知，H/d=5的悬臂圆柱临界雷诺数应在4×105左右，远大于二维圆柱对应值.亚临界区内，H/d = 5悬臂圆柱Cd明显小于二维圆柱;而超临界区内则明显大于后者.H/d = 5悬臂圆柱Cd在临界区内减小了约53%;而二维圆柱则减小了约83%，即二维圆柱在临界区内的阻力下降更为显著.

图3给出了不同高度处局部时均阻力系数的CdRe曲线.可以看出，尽管试验中悬臂圆柱绝大部分处于均匀来流中，但不同高度的局部Cd仍存在显著差异.总体来看，各高度处的CdRe曲线均存在3个区间，这与二维圆柱定性上是类似的.亚临界区内，越接近柱体自由端，Cd越大.而超临界区内，z* = 4.5处的Cd最大，中间高度z* =2.5处Cd相对最小.仔细观察图3可发现，不同高度处的临界雷诺数并不相同.z*=4.5与4处比z*=2.5与1提前进入临界区，即靠近自由端附近的流动会首先进入临界区，这一现象将在2.2与2.3节中详细讨论.

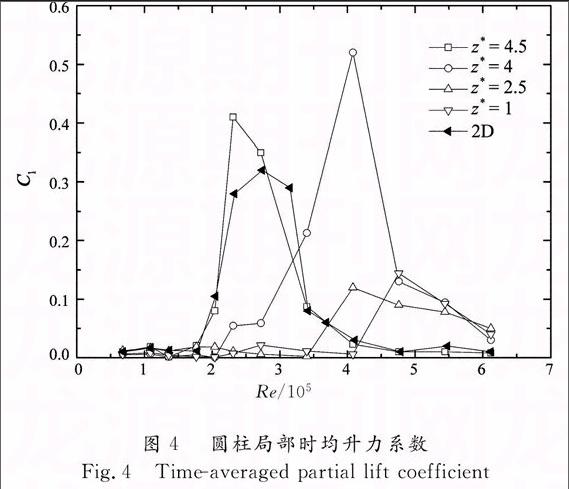
图4给出了悬臂圆柱局部时均升力系数的ClRe曲线，还给出了二维圆柱对应结果以供对比.

对于二维圆柱，亚临界区内的Cl基本为零;临界区内，Cl随Re的增大先增大后减小，当Re ≈ 2.6×105时，Cl出现最大值0.32.进入超临界区后，Cl又基本恢复为零.而悬臂圆柱不同高度处出现Cl大幅上升所对应的Re不相同，越接近自由端对应的Re数越小.如图4所示，z*= 4.5处Cl上升对应的Re

≈ 2.0×105;而z*= 4处则在Re > 2.8×105后才出现Cl的大幅上升.更接近底部平面的z*= 2.5和1处，Cl上升的幅度相对较弱，且对应的Re也更大.Cl的大幅上升是与临界区内圆柱某侧首先出现分离泡而形成的风压不对称现象有关.上述现象再次证明悬臂圆柱不同高度上对应的临界雷诺数是不同的.

2.2表面风压

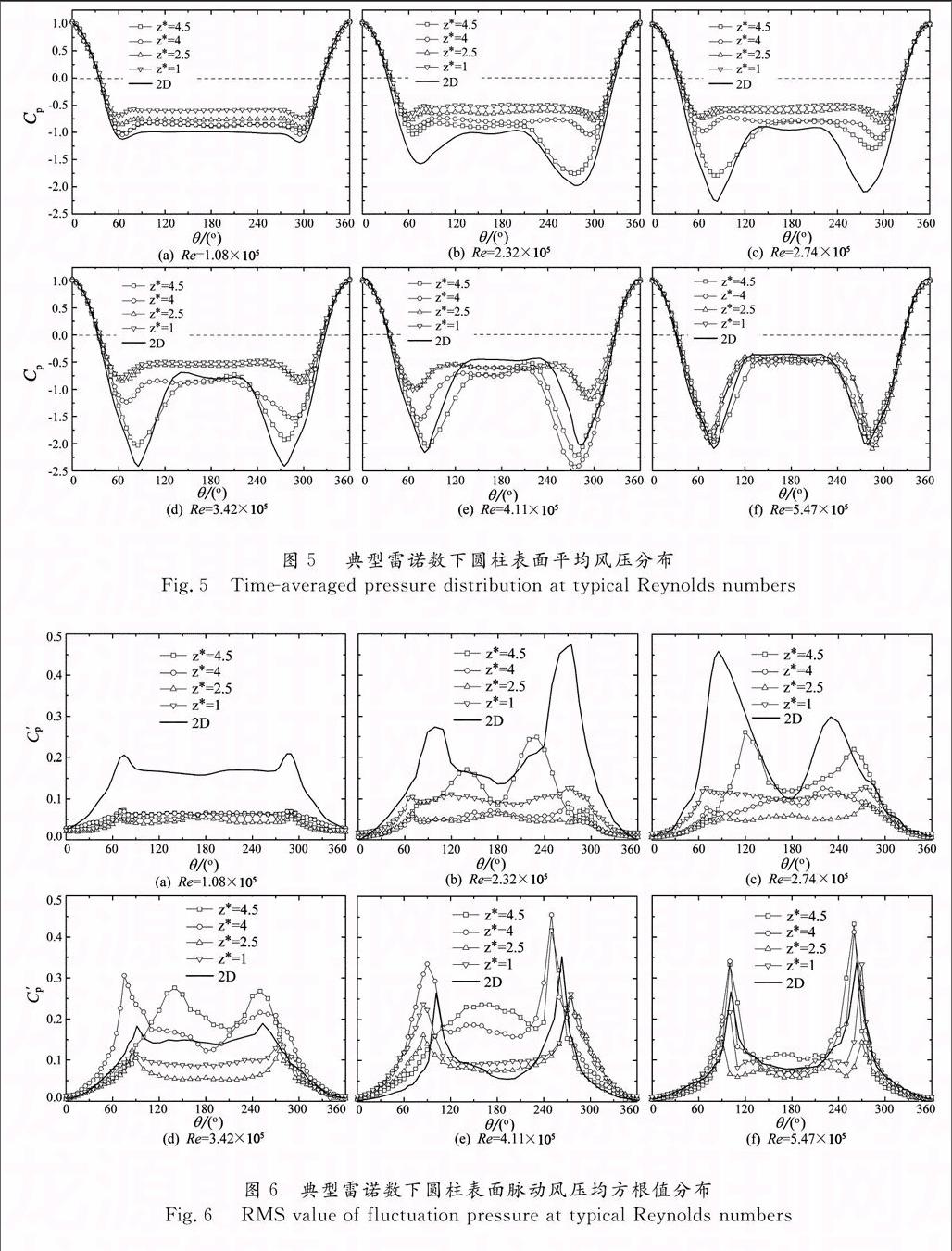
图5和图6分别给出了典型雷诺数下悬臂圆柱不同高度的时均与脉动风压分布，图中二维圆柱对应结果用实线给出以供对比.由图5可知，不同高度处Cp差异主要出现在分离点附近以及背风侧，而迎风侧Cp分布则基本相同.当Re = 1.08×105，即处于亚临界区时，所有高度上的时均风压均为对称分布.各高度迎风侧驻点（θ = 0°）Cp均为1.随着θ的增大，Cp迅速减小，当θ ≈ 35°时，风压变为负值，这与二维圆柱情况类似.随着θ的逐渐增大，Cp继续减小至最小值Cp_min，然后略为增大并在背风侧大部分区域内保持恒定.可以看出，Cp_min及其所对应的角度在不同高度上均不相同.从自由端向下Cp_min分别为-1.04，-1.02，-0.84和-0.69，对应θ约分别为65°，65°，62°和60°.由此可知，在亚临界区，越接近自由端，Cp_min越低，且其对应的方位角更大;越接近自由端，柱体背压（Cpb）最低，但始终高于二维圆柱的背压.

由图5（b）可知，当Re = 2.32×105时，z*=4.5处的Cp出现了不对称分布，与二维圆柱结果定性上类似.其一侧Cp_min减小至约-1.75，而另一侧相对于亚临界无明显变化.此时其他高度处的Cp仍为对称分布且与亚临界区（如图5（a）所示）基本相同.造成上述不对称风压分布的原因是圆柱一侧首先出现了分离泡，而另一侧则没有[6].出现分离泡的一侧Cp_min对应角度明显向下游推迟.随着Re的增大至2.74×105，z*=4.5处的Cp仍不对称，且z*=4处的Cp也表现出向不对称转变的趋势.值得注意的是，z*=4.5处的Cp_min在图5（b），5（c）中出现在了柱体不同的两侧，这是由于临界区内圆柱表面分离泡可能随机出现在柱体任何一侧.

当Re增大至3.42×105时（图5（d）），z*=4.5处Cp已基本恢复为对称状态，而z*=4处Cp仍处于临界区的非对称状态.此时，z*=2.5和1处Cp仍处于亚临界区.这表明即使在均匀来流中，悬臂圆柱不同高度可能处于不同的流动状态，即当自由端附近流动已进入超临界区时，柱体中部与底部流动仍处于亚临界区.随Re进一步增大至5.47×105以上，如图5（f）所示，z*=2.5和1高度处Cp也进入了超临界区.相对于亚临界区，此时悬臂圆柱不同高度处的Cpb变得非常接近且近似等于二维圆柱的对应值.

图6给出了C′p随Re的变化情况，总的来看，不同高度处C′p分布所表现出的雷诺数效应也不尽相同.悬臂圆柱自由端附近的C′p首先进入临界区，而柱体中部与底部进入临界区相对较晚.这一现象与图5所示Cp雷诺数效应的规律是类似的.此外，亚临界区内悬臂圆柱的C′p远小于二维圆柱的对应值，约相当于后者的1/4;而超临界区内，两者C′p基本相当.这可能是因为，亚临界区内C′p主要受周期性的漩涡脱落影响，而悬臂圆柱的卡门涡街远弱于二维圆柱;但在超临界区，不存在周期性漩涡脱落，C′p主要受到圆柱表面湍流边界层的影响.

2.3雷诺数区间的划分

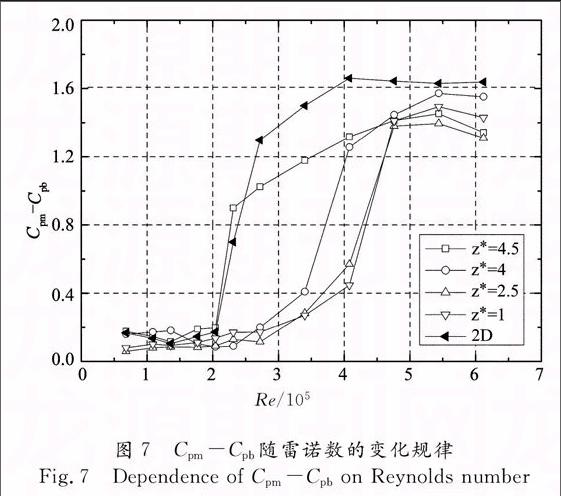
由2.1与2.2节可知，悬臂圆柱气动力会表现出强烈的雷诺数效应，且不同高度所对应的临界雷诺数并不相同.为准确确定各高度所对应的雷诺数区间，可用风压极小值与背压之差Cpm-Cpb作为评价指标[15，21]，如图7所示.对于二维圆柱，当Re ≤ 2.0×105时，Cpm-Cpb非常小且基本不随Re变化，该范围即为亚临界区;2.0×105 < Re ≤ 4.0×105，Cpm-Cpb随Re增加而迅速增大，该范围为临界区;而Re > 4.0×105后，Cpm-Cpb又基本不随Re变化，此时已进入超临界区.其中2.0×105可视为亚临界区向临界区转变所对应的临界雷诺数.

悬臂圆柱不同高度Cpm-Cpb随Re的变化规律与二维圆柱存在显著差别.z* = 4.5处，临界雷诺数为2.0×105，这与二维圆柱类似.随Re的进一步增大，Cpm-Cpb逐渐增大，直至Re ≈ 5.5×105，Cpm-Cpb才达到最大值，即z* = 4.5处临界雷诺数范围约为2.0×105 < Re < 5.5×105.对于z* = 4处，Cpm-Cpb迅速增大处所对应的临界雷诺数约为2.7×105.对于z*=2.5 和1处，Cpm-Cpb迅速增大所对应的临界雷诺数更大，约为3.0×105左右.由此可知，悬臂圆柱的临界雷诺数在不同高度上并不相同，z* = 4.5临界雷诺数Re = 2.0×105;z* = 4处为2.7×105，而z* = 2.5和1处约为3.0×105.此外，悬臂圆柱不同高度处由临界区变化为超临界区所对应的雷诺数基本相等，都为Re = 5.5×105左右，远大于二维圆柱的对应值.

3结论

通过风洞试验对均匀流中H/d = 5的悬臂圆柱气动力进行了测量，试验雷诺数为0.68×105～6.12×105，涵盖了亚临界、临界与超临界区间.通过本文研究可得到如下结论：

1）悬臂圆柱气动力与二维圆柱类似，也具有明显的雷诺数效应，存在亚临界、临界、超临界区.亚临界区内，悬臂圆柱局部阻力系数沿展向存在明显差异，越接近自由端背压越低、阻力系数越大，但都明显小于二维圆柱对应值.

2）临界区内，悬臂圆柱平均风压分布不对称，时均升力不为零，且越接近自由端时均升力值越大.悬臂圆柱阻力系数在临界区内的下降幅度远小于二维圆柱的对应值;在超临界区内，风压恢复对称分布，时均升力降为零，悬臂圆柱各高度局部阻力系数均大于二维圆柱对应值.

3）均匀流中的悬臂圆柱，其总体阻力系数由亚临界区至临界区转变所对应的临界雷诺数大于二维圆柱对应值.悬臂圆柱不同展向高度上临界雷诺数不相同，越接近自由端，临界雷诺数越小.均匀流中的悬臂圆柱体可能会出现自由端附近已进入临界区甚至超临界区，而柱体下半部仍处于亚临界区的状态.

参考文献

[1]顾明， 王新荣.工程结构雷诺数效应的研究进展[J]. 同济大学学报：自然科学版， 2013， 41（7）：961-968.

GU Ming， WANG Xinrong. Research progress of Reynolds number effect of engineering structures[J]. Journal of Tongji University：Natural Science，2013，41（7）：961-968.（In Chinese）

[2]SCHEWE G. Reynoldsnumber effects in flow around moreorless bluff  bodies[J].Journal of Wind Engineering and Industrial Aerodynamics，2001， 89（14/15）：1267-1289.

[3]HOXEY R P， REYNOLDS A M， RICHARDSON G M，et al. Observations of Reynolds number sensitivity in the separated flow region on a bluff body[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1998， 73（3） ：231-249.

[4]HIGUCHI H， KIM H J，FARELL C. On flow separation and reattachment around a circular cylinder at critical Reynolds numbers [J]. Journal of Fluid Mechanics， 1989， 200： 149-171.

[5]WILLIAMSON C H K. The existence of two stages in the transition to threedimensionality of a cylinder wake[J]. Physics of Fluids， 1988， 31（11）： 3165-3168.

[6]BEARMAN P W. On vortex shedding from a circular cylinder in the critical Reynolds number regime[J]. Journal of Fluid Mechanics， 1969， 37： 577-585.

[7]杜晓庆，顾明. 临界雷诺数下斜拉桥拉索的平均风压和风力特性[J]. 空气动力学学报，2010，28（6）： 639-644.

DU Xiaoqing ， GU Ming. Wind pressure distribution and aerodynamic characteristic of stay cable in the critical Reynolds number regime[J]. Acta Aerodynamica Sinica，2010，28（6）：639-644.（In Chinese）

[8]刘庆宽，郑云飞，马文勇，等. 雷诺数效应对斜拉索气动特性的影响[J]. 工程力学，2013，30（6）： 284-289.

LIU Qingkuan， ZHENG Yunfei， MA Wenyong，et al.  Reynolds number effect on aerodynamic characteristics of staycables[J]. Engineering Mechanics，2013，30（6）：284-289.（In Chinese）

[9]王磊，梁枢果，邹良浩，等. 超高层建筑抗风体型选取研究[J]. 湖南大学学报：自然科学版，2013，40（11）：34-39.

WANG Lei， LIANG Shuguo， ZOU Lianghao， et al. Study on the body shape selection of super highrise building from the point of wind resistance[J]. Journal of Hunan University： Natural Sciences， 2013， 40（11）： 34-39. （In Chinese）

[10]李正农，郝艳峰，刘申会. 不同风场下高层建筑风效应的风洞实验研究[J]. 湖南大学学报：自然科学版，2013，40（7）：9-15.

LI Zhengnong， HAO Yanfeng， LIU Shenhui. Wind tunnel of tall building wind effect in different geomorphologic terrain categories[J]. Journal of Hunan University：Natural Sciences， 2013， 40（7）： 9-15. （In Chinese）

[11]FOX T A，WEST G S. Fluidinduced loading of cantilevered circular cylinder in a lowturbulence uniform flow. part 2： fluctuating loads on a cantilever of aspect ratio of 30[J]. Journal of Fluids and Structures， 1993， 7（1）： 15-28.

[12]BABAN F， RMC S. Aspect ratio effect on flowinduced forces on circular cylinders in a crossflow[J]. Experiments in Fluids， 1991， 10： 313-321.

[13]OKAMOTO T，SUNABASHIRI Y. Vortex shedding from a circular cylinder of finite length placed on a ground plane[J]. Journal of Fluids Engineering， 1992， 114： 512-521.

[14]OKAMOTO T，YAGITA M. The experimental investigation on the flow past a circular cylinder of finite length placed normal to the plane surface in a uniform flow[J]. Bulletin of JSME， 1973， 16： 805-814.

[15]UEMATSU Y，YAMADA M. Effects of aspect ratio and surface roughness on the timeaveraged aerodynamic forces on cantilevered circular cylinders at high Reynolds numbers[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1995， 54： 301-312.

[16]WANG H F， ZHOU Y， MI J. Effects of aspect ratio on the drag of a wallmounted finitelength cylinder in subcritical and critical regimes[J].Experiments in Fluids，2012，53（2）：423-436.

[17]BASU R I. Aerodynamic forces on structures of circular crosssection， part 1. modelscale data obtained under twodimensional conditions in lowturbulence streams[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1985， 21： 273-295.

[18]BASU R I. Aerodynamic forces on structures of circular crosssection， part 2. the influence of turbulence and threedimensional effects[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1986， 24： 33-59.

[19]FARELL C， BLESSMANN J. On critical flow around smooth circular cylinders[J]. Journal of Fluid Mechanics， 1983， 136： 375-391.

[20]GU Z F， SUN T F. On interference between two circular cylinder in staggered arrangement at high subcritical Reynolds number[J]. Journal of Wind Engineering and Industrial Aerodynamics， 1999， 80： 287-309.

[21]GUVEN O， FARELL C， PATEL V C. Surfaceroughness effects on the mean flow past circular cylinders[J]. Journal of Fluid Mechanics， 1980， 98（4）： 673-701.