基于卷积神经网络气动力降阶模型的翼型优化方法*
2022-02-18王沐晨李立州黄钰棋
王沐晨,李立州,张 珺,黄钰棋,张 林,石 玥
(1.中北大学 机电工程学院,太原 030051;2.太原学院 数学系,太原 030001)
引 言
近年来,计算流体力学(computational fluid dynamics,CFD)成为发动机和飞行器翼型气动设计和优化的重要手段.但是,气动优化[1]需要大量反复的CFD 分析,消耗的计算资源过大.因此,如何快速准确地获得不同形状参数下翼型的气动力成为这类优化的难点.
为解决这一问题,20世纪90年代Dowell[2]和Silva[3]提出了气动力降阶模型方法(reduced order model,ROM),强调在计算精度不低于CFD的同时,大幅提高气动分析的效率[4-7].李立州等[8]用Volterra 级数降阶模型建立了尾流激励的发动机叶片气动力预测方法,可以快速预测上游时变尾流激励下叶片气动力振荡.He[9]总结了用于叶轮机械流体分析的Fourier 方法.王梓伊等[10]和Zhang 等[11]以径向基函数振型和PCA 振型为基模态,提出了可变结构的非定常气动力降阶模型方法.Yao 等[12]采用谐波平衡法(harmonic balance,HB)法,研究了自由流中固定圆柱体涡激振动的锁频现象.Zhang 等[13]采用流固耦合气动弹性方法和系统辨识技术建立了降阶模型,通过ROM 提供的特征分析了系统的稳定性和振动模态.罗骁等[14]基于谐波平衡法建立了尾流激励叶片振动降阶模型,可以准确地预测尾流激励下的叶片振动.张鸿志等[15]通过本征正交分解法(proper orthogonal decomposition,POD)建立了气动弹性降阶模型.Li 等[16]提出了一种基于弱非线性气动力降阶模型的多步优化方法,可以预测和优化跨音速翼型气动力.张珺等[17]提出了一种基于弱非线性气动力降阶模型的翼型优化方法.
现有气动力降阶模型大多适用于小扰动问题,在扰动较大时精度下降很快.为解决这一问题,越来越多的研究者讨论用神经网络建立非线性气动力降阶模型[18-19].尹明朗等[20]提出了一种基于CFD 带验证信号的气动力降阶模型,用于跨声速气动力预测,加强了模型在不同频率和振幅下的泛化能力.Kou 等[21]提出了一种多核神经网络降阶模型,并将其应用于非线性非定常气动力问题.本文基于卷积神经网络(convolutional neural networks,CNN)模型,建立了形状大扰动情况下的翼型非线性气动力降阶模型,采用该降阶模型对翼型进行优化,讨论了训练信号数据降维对该降阶模型精度的影响.
1 基于卷积神经网络气动力降阶模型的翼型优化方法
1.1 翼型径向基函数参数化方法

采用径向基函数(radial basis function,RBF)对翼型进行参数化,具体方法是将原翼型与参数化的扰动叠加,形成新的翼型:式中,yu0(x)和yu(x)为原上翼面形状与扰动后上翼面形状,x为翼型上表面的横坐标,yd0(x)和yd(x)为原下翼面形状和扰动后下翼面形状,fk(x)为径向基函数,ai为上翼面形状控制参数,bi为下翼面形状控制参数,xk为径向基函数节点位置,取x1=0.15,x2=0.25,x3=0.35,x4=0.45,x5=0.55,x6=0.65,x7=0.75.
1.2 卷积神经网络气动力降阶模型
卷积神经网络[22]作为一种深度学习神经网络模型,在非线性大扰动问题的预测上具有优势.针对问题的非线性程度的不同,可以对神经网络模型深度、激活函数等进行设计,得到适当的卷积神经网络模型.通过卷积神经网络预测值与真值的误差的反向传播,可以对卷积神经网络模型进行训练[23].
卷积神经网络通常由输入层、池化层、卷积层、全连接层和输出层组成(图1).第l层卷积神经网络的计算公式如下:

图1 卷积神经网络结构图Fig.1 The convolutional neural networks’ structure diagram

式中,Xnl表示第l层输出值的第n个特征,Wnl表示第l层第n个卷积核的权重矩阵,表示第l−1层的输出,eln表示偏置项,g(·)表示激活函数.
通常选择ReLU 函数作为激活函数[24],其公式如下:

本文用卷积神经网络模型,建立形状参数非线性大扰动下翼型的气动力降阶模型.
翼型参数变化对气动力影响可以表示为

其中,p(x)为压力系数,τ(x)为摩擦因数,ψ为气动力系统模型.
将式(1)代入式(5)可得翼型参数对气动力影响的模型:
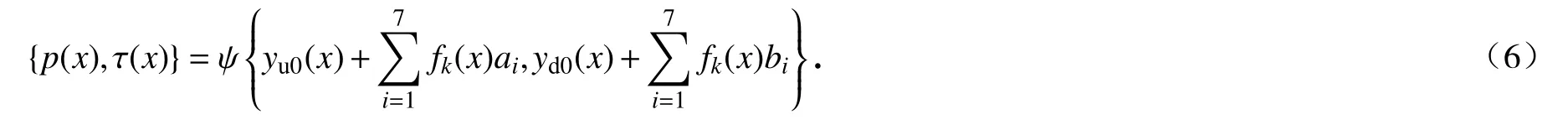
由于yu0,yd0和fk均已知,故翼型参数对气动力影响的模型可以简化为

用式(3)和(4)表示式(7),可得翼型压力系数p′n(x)和 摩擦因数τ′n(x)的第一层卷积神经网络模型:
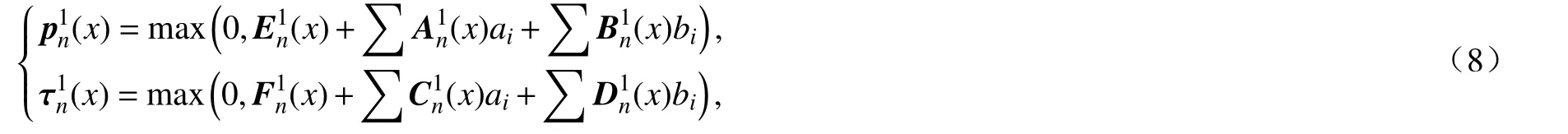
式中,A1n(x)和B1n(x)为p1n(x)对 应的第一层第n个卷积核的权重,C1n(x)和D1n(x)为τ1n(x)对应的第一层第n个卷积核的权值,E1n(x)和F1n(x)为第一层p1n(x),τ1n(x)的偏置项.
由式(1)可知,中间层的卷积模型可以表示为

式中,pln(x),τln(x) 表示第l层卷积层的输出结果,表示第l−1层的输出结果,Rln,Qln分别表示压力系数pln(x) 、摩擦因数τln(x)对 应的第n个权值,eln,dnl分别表示压力系数pln(x) 、摩擦因数τln(x)对应的偏置项.
最后一层卷积层与输出层采用linear 函数结合,构建卷积神经网络全连接层进行激活输出,其函数表示为

式中,pmn(x),τmn(x)表示最后一层卷积层的输出结果,Gn,Hn分别表示压力系数pn(x)、摩擦因数 τn(x)对应的第n个权值,Ln,Kn分别表示压力系数pn(x)、摩擦因数τn(x)对应的偏置项.
2 卷积神经网络气动力降阶模型方法的算例
2.1 算例说明
以NACA0012 翼型为初始翼型,验证基于卷积神经网络的气动力降阶模型方法.采用CFD 模拟得到不同参数翼型的气动力数据,模拟采用Spalart-Allmaras 湍流模型,理想气体,攻角为0◦,温度为300 K.因为NACA0012为对称翼型,上、下翼面参数对气动力的影响也是对称的,故本文只给出了上翼面参数调整后的气动力数据.这些翼型(图2)和气动力数据(图3)被用于训练卷积神经网络气动力降阶模型.
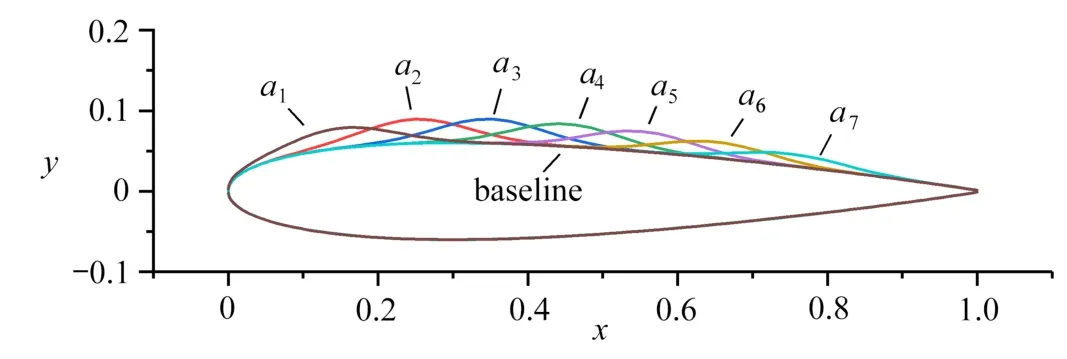
图2 不同参数的翼型Fig.2 Airfoils with different parameters
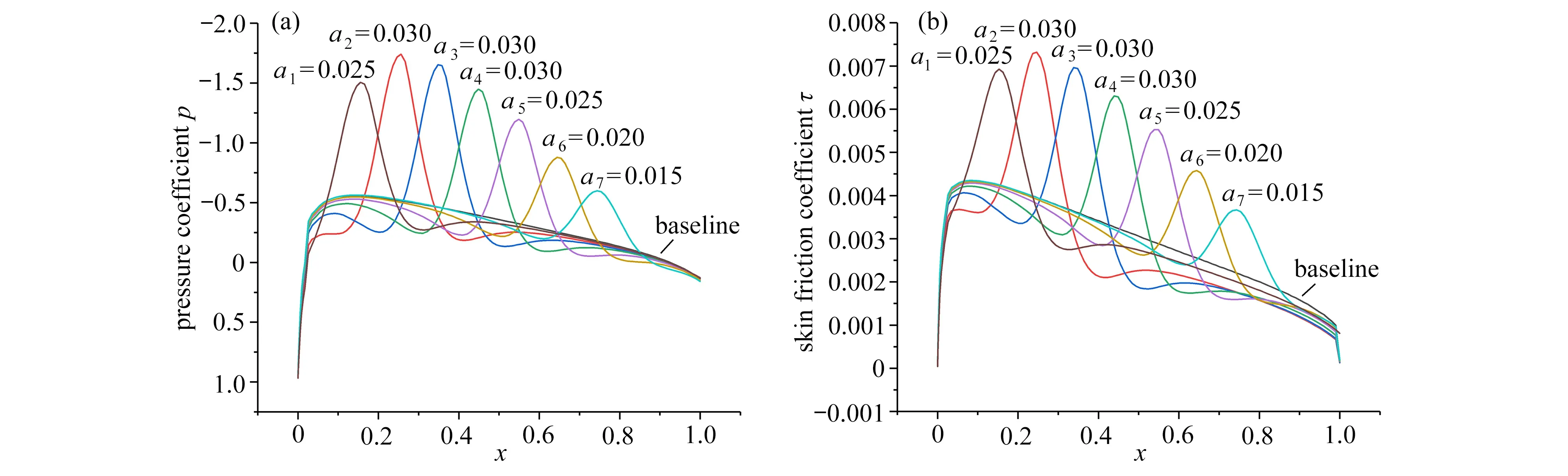
图3 不同参数翼型的气动力:(a) 压力系数p;(b) 摩擦因数τFig.3 Aerodynamics of the airfoils with different parameters:(a) pressure coefficient p;(b) skin friction coefficient τ
2.2 卷积神经网络气动力降阶模型的训练
将翼型的形状参数作为输入,翼型的气动力作为输出,训练卷积神经网络气动力降阶模型.训练好的降阶模型可以用来预测不同形状翼型的气动力.为了降低卷积神经网络气动力降阶模型的阶数和参数个数,采取参数池化(parameterized pooling,PP)法[25]和RBF 拟合法对气动力数据进行降维,然后再进行卷积神经网络气动力降阶模型的训练.为方便比较,本文也给出了气动力不降维的卷积神经网络降阶模型.也就是说,本文总计给出了3 种卷积神经网络气动力降阶模型.
采用这3 种卷积神经网络气动力降阶模型和CFD 模型,计算了一种新形状参数下翼型(图4)的气动力.图4中新翼型的参数扰动量为形状控制点翼型厚度的25%.图5中CFD为仿真结果,AOD为气动力数据未降维的结果,PP为气动力数据池化降维的结果,RBF为气动力数据径向基拟合降维的结果.从图5的结果看出,卷积神经网络气动力降阶模型有着很高的精度,气动力数据RBF 拟合降维的降阶模型更为精确.根据分析可知:气动力数据降维会使神经网络模型中待定参数的个数减少,在气动力数据相同的情况下数据降维的神经网络降阶模型的参数更少,收敛更好,预测精度相应地会更高.从图4和图5可以看出翼型变化比较大,但气动力预测的精度依然较高,由此可知卷积神经网络气动力降阶模型可以预测较大扰动下的翼型气动力.

图4 大扰动的翼型Fig.4 Airfoils of large disturbance

图5 翼型气动力:(a) 压力系数p;(b) 表面摩擦因数τFig.5 Airfoil aerodynamics:(a) pressure coefficient p;(b) skin friction coefficient τ
2.3 基于卷积神经网络气动力降阶模型的翼型优化
基于精度最高的RBF 气动力数据降维的降阶模型,采用遗传算法,以翼型形状参数为设计变量,以增加最大升阻比为优化目标,进行优化.为防止优化过程中出现翼型畸形的情况,将各翼型参数的最大扰动量设置为形状控制点翼型厚度的25%.翼型各参数的上、下限和优化结果如表1所示.
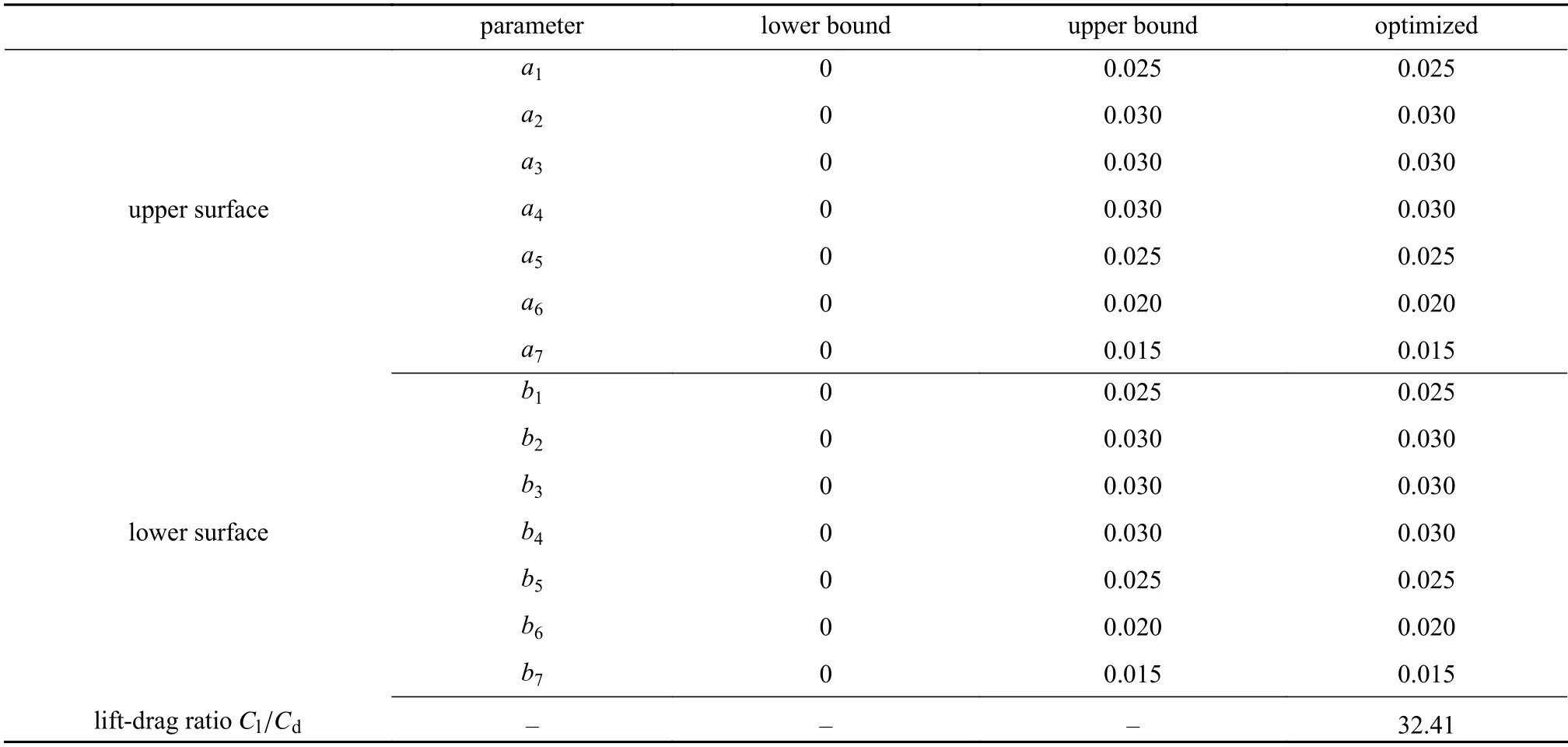
表1 翼型优化结果Table 1 Airfoil optimization results
采用精度最高的RBF 气动力数据降维的降阶模型优化翼型,结果如图6所示.图7给出了优化得到翼型的压力系数和摩擦因数.为了检验降阶模型的优化结果,用CFD 计算该翼型的压力系数和摩擦因数.从结果来看:采用RBF 气动力数据降维的卷积神经网络气动力降阶模型的气动力数据与CFD的结果一致.
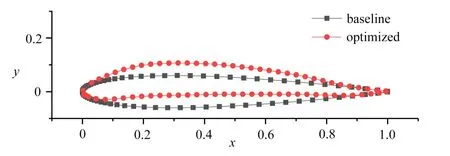
图6 翼型优化结果Fig.6 Airfoil optimization results
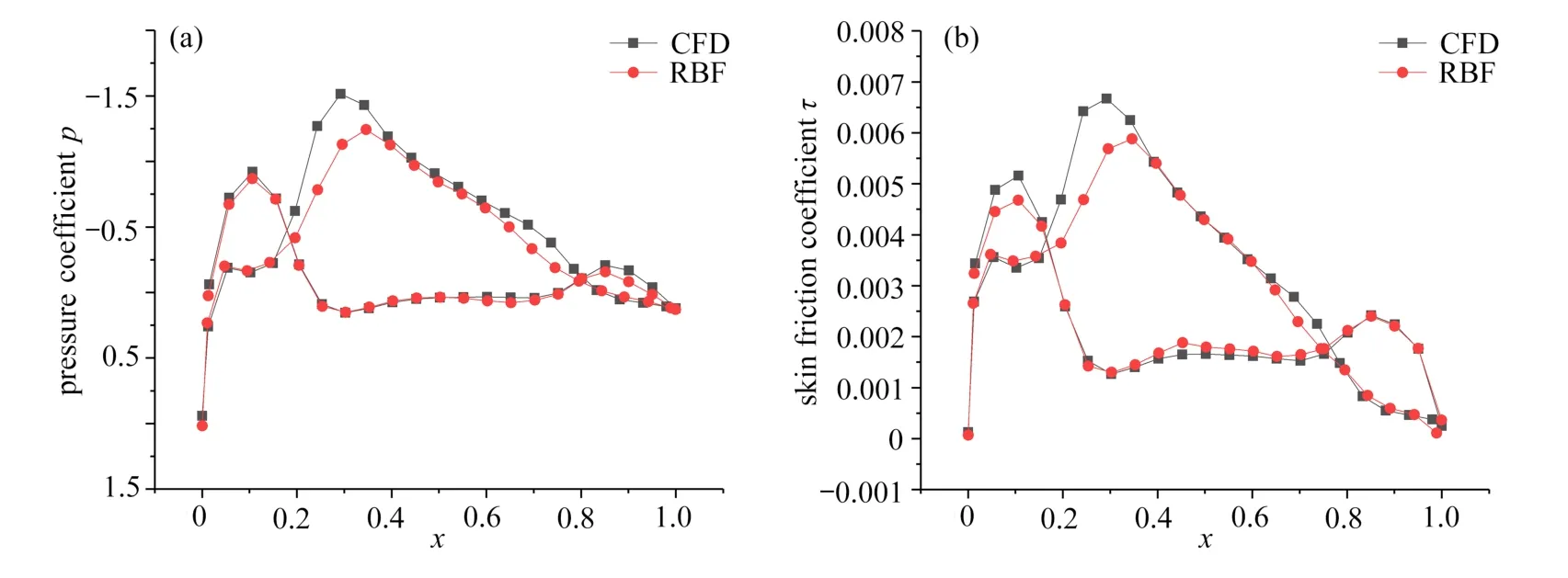
图7 气动力降阶模型的优化结果:(a)压力系数p;(b)摩擦因数τFig.7 Aerodynamic ROM optimization results:(a)pressure coefficientp;(b)skin friction coefficient τ
3 总 结
本文研究了基于卷积神经网络气动力降阶模型的翼型气动力优化方法,其主要思想是用卷积神经网络建立参数对翼型气动力影响的降阶模型,用该气动力降阶模型预测形状参数大扰动下翼型的气动力,并用该降阶模型优化翼型的气动力.算例的结果表明:在形状参数大扰动的情况下,卷积神经网络气动力降阶模型可以较为准确地预测翼型气动力;采用卷积神经网络气动力降阶模型优化翼型的方法是可行的.本文讨论了气动力训练数据的池化降维法和RBF 拟合降维法对卷积神经网络气动力降阶模型精度的影响,结果表明:气动力训练数据降维会使神经网络模型中待定参数的个数减少,在训练数据相同的情况下数据降维的神经网络降阶模型的收敛会更好,预测精度会更高.
