一题多解与一题多变拓展学生思维能力的尝试

摘 要：文章主要尝试通过一题多解与一题多变拓展学生思维能力，首先对一题多解与一题多变拓展学生思维能力问题的必要性、可行性、意义进行了梳理，然后结合中考模拟题进行了一题多解与一题多变练习的思路详解，最后对一题多解与一题多变拓展学生思维能力的尝试进行了简单总结。

关键词：一题多解;一题多变;拓展思维能力

中图分类号：G633.6              文献标识码：A                文章编号：2095-624X（2021）35-0055-02

一题多解与一题多变是培养学生掌握数学方法的有效途径，也是培养学生发散思维能力的方式之一。在数学学习中，有些问题的综合性较强，数量关系较多，这就会出现一题多解与一题多变的现象。有些题目可以通过多种途径得到解答，正所谓“殊途同归”。在处理这类题目时，学生如果能够准确理解条件，正确运用各种数量关系，通过多种途径解决问题，做到一题多解，有利于培养他们分析问题的能力，解決问题的能力，锻炼发散思维能力。而一题多变，可以使学生对简单的问题进行多方位、多角度的探索尝试，在这一基础上，让学生提升解决更多新问题，进而拓展学生思维能力。下面通过一个例题来说明笔者的一些尝试。

一、一题多解拓展学生思维能力的尝试

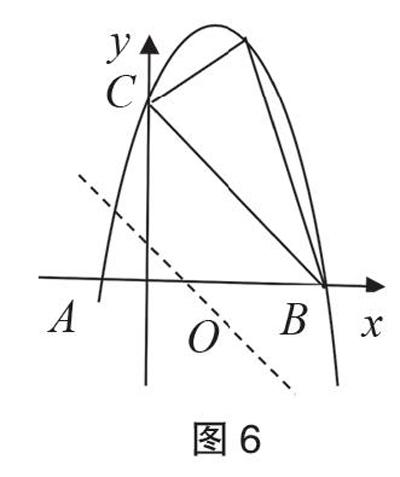
例题  如图1，抛物线y=ax2+bx+c与x轴交于A（-1，0）、B（3，0），与y轴交于C（0，3）。

（1）求抛物线y=ax²+bx+c的解析式。

（2）P为直线BC上方的抛物线上的一个动点，当△PBC面积最大时，求点P的坐标，并求出△PBC的最大面积。

分析：（1）抛物线的解析式有三种形式：一般式、交点式、顶点式。本题中，已知抛物线所过三点坐标，因此可以用一般式的方法;因为所过三点中的A、B两点是抛物线与x轴的交点，因此还可以运用交点式的方法。

（1）方法一：用一般式

实践证明，经常通过上述对一道题进行多种变化并解决问题，也就是进行一题多变练习，可以更进一步培养、提高学生分析问题、解决问题的能力，锻炼学生思维能力。

综上所述，在初中数学教学中，教师对有代表性的问题一定要充分利用，不失时机地对学生进行一题多解和一题多变练习，有意识地培养学生思维能力，并使学生养成一题多解和一题多变习惯，培养遇到问题进行一题多解和一题多变练习的意识，使学生得到更好的思维训练，这样，教学也势必会取得事半功倍的效果。

[参考文献]

[1]韩云凤.“一题多解”与“多题一解”在高中数学教学中的价值[J].数学学习与研究，2019（24）：108.

[2]阚志超.“一题多解”与“多题一解”在高中数学教学中的价值研究与实践[J].中国校外教育，2015（29）：23.

[3]闫萧寒.“一题多解”与“多题一解”在提升中学数学教学质量中的应用[J].求知导刊，2014（12）：100-101.

作者简介：褚领群（1970— ），男，河北石家庄人，中学高级教师，本科，研究方向：中学数学教学。