删失截断下新冠疫情初期数据多变点Bayes估计

刘 君 罗晓媛

(黑河学院 理学院，黑龙江 黑河 164300)

2020年，新冠病毒肆虐全球。在此期间，病例确诊的间隔时间服从指数分布。间隔数据发生突变的时刻即为变点，利用指数分布估计间隔时间的变点位置，有助于认清疫情发展程度和防控开展。一些感染者在救治过程中由于死亡而中断数据记录或由于某种原因中途退出数据统计，这便是右删失。另外，在无症状感染者未被检测或感染者未确诊就病亡时，缺失了最初的确诊记录数据，这就是左截断。左截断和右删失同时出现在新冠疫情的现存确诊病例数据中，于是产出了本论题。

EM算法和MCMC算法是两种常用的数据添加算法，使贝叶斯统计中许多计算化难为简,应用广泛[1]。EM算法为后验分布众数的求解迭代方法，每一步迭代由E步期望值和M步极大值组成；MCMC法是将Gibbs抽样和Metropolis-Hastings算法相结合得到联合样本，对后验分布的各统计量进行估计的方法[2]。

1 删失截断数据下指数分布的似然函数

设(X,Y,Z)是三维随机变量，且X,Y,Z都服从指数分布，其中随机变量X为病例确诊间隔时间，其分布函数为概率密度为f(x；λ)，λ是未知参数；Y为右删失随机变量，分布函数为G(y)，概率密度为g(y)；Z为左截断随机变量，分布函数为H(z)，概率密度为h(z)。X,Y,Z取值大于零且两两相互独立。令

2 删失截断数据下指数分布多变点的Bayes估计

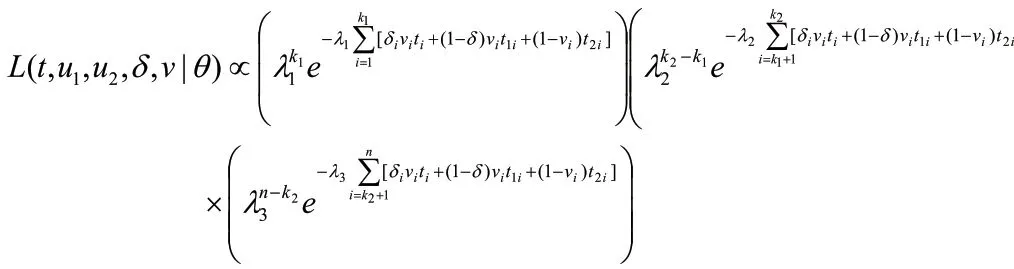
各参数的先验分布如下：

(1)(k1,k2)的无信息先验分布

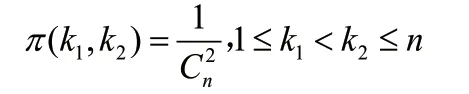
(2)(λ1,λ2,λ3)的无信息先验分布

当(k1,k2)与(λ1,λ2,λ3)相互独立时，有

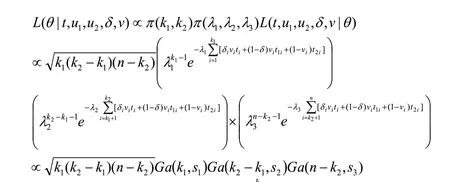
根据各参数的满条件分布，利用MCMC方法获取各参数的平稳后验分布。t1i由逆变换法抽取，t2i由合成法抽取，可采用Gibbs抽样；k1，k2带有复杂的参数约束条件，Gibbs抽样困难，可进行Metropolis-Hastings算法抽样。

3 MCMC方法的具体步骤

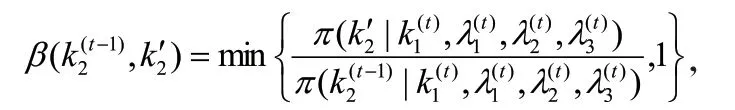
重复M次迭代可得到样本容量为M的独立同分布的5维Gibbs联合样本，其中因初始不稳定而舍弃M0个样本，将剩余的M-M0个稳定样本均值作为各参数的Bayes估计。即

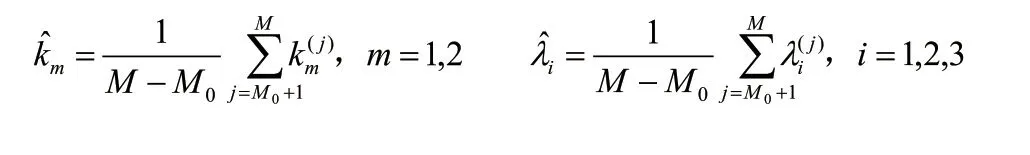
4 病例确诊间隔时间删失截断数据多变点Bayes估计

取我国某省新冠疫情2019年12月1日至2021年1月6日的病例确诊间隔时间数据，绘制概率密度函数，如图1所示。

图1 病例确诊时间间隔概率密度

利用R软件，采用MCMC法估计变点k1，k2的位置，先进行10000次预迭代，再进行10000次迭代，运行结果，见表1。

表1 参数k1、k2、λ1、λ2、λ3的Bayes估计结果

结果表明，根据当前防控状态，小范围新冠疫情期间，病例确诊时间间隔的变点位于2.3528天和5.2923天两个位置，即疫情防控措施及时的情况下，病例确诊间隔时间为2天时，表明疫情由不受控向受控转变，病例确诊时间间隔为5天时，疫情控制进入到稳定转态，2天和5天的病例确诊间隔时间是疫情有效控制的明显标志。