基于二元分割的多变点估计
2020-06-03夏美美赵联文范元静
夏美美, 赵联文, 范元静, 杨 航
(西南交通大学数学学院,成都 611756)
变点问题一直是统计学中的焦点话题之一. 变点问题在1954年由Page提出,该问题的提出源于工业生产的质量控制过程[1],生产过程中产品质量在相当长的时间内保持大致恒定的输出,当过程中某个阶段出现故障时,产品质量恶化,大部分产品质量变得不可接受,此刻希望能够停止生产或者发出预警,避免产出更多不合格的产品,该故障发生时刻称为变点. 陈希孺[2]给出了变点问题的一般提法,我们有一系列的观察值(样本),在多数情况下,这些观察值按其出现的时间进行先后排列,在某个未知的时刻,样本的分布或其数字特征发生突然变化,这个时刻就是变点. 由于变点发生时刻是未知的,因此变点问题研究的主要目的在于估计变点的个数和位置,同时围绕变点估计量的相合性、渐进分布以及变点的跳跃度、收敛速度等进行理论分析.
随着问题的深入研究,变点统计推断已经应用到经济、金融、生物医学、气象学、地质学等很多领域. 如金融领域中[3],由于政治因素或潜在金融危机的影响,导致股市存在大的波动,通过对序列或过程中存在的变点做出相应的估计,为金融危机等事件的监测及预测提供有用的信息,从而帮助人们达到规避金融风险的目的;在智能交通系统[4]中,通过对交通流数据的变点分析,实时监控当前和未来短时交通状况,使车辆避开拥挤区域或使驾驶员降低行车速度,从而达到平稳交通流、减轻区域交通压力的目的;在地质学中[5],对地质信号的变点分析,有助于检测地下岩层中比较突出的断层,从而能够及时对地质勘探以及地震预防等起到指导作用;在视频监控系统中[6],将原始视频分割成多个镜头,再对相似镜头进行合并,将冗长的监控视频处理为简短、准确、包含视频主要信息的视频摘要,安保人员可以通过浏览视频摘要快速做出防范,被广泛应用于电影编辑、道路交通、国家安防等各个方面. 因此,变点分析不仅有重要的理论意义,许多实际问题也可以通过转换为变点分析问题进行解决,这也是近年来变点问题受到统计学以及更多学科研究学者重视的原因.
对于单个变点问题的研究已经比较成熟,但在互联网时代下,数据维度、数量激增,单个变点问题的研究不能满足实际应用,因此多变点统计推断问题亟须解决. 多变点估计问题不仅要估计变点的位置,也要确定变点的数目. 本文重点研究正态分布序列中均值多变点的估计问题,该问题可以简述为:考虑模型Xi=μi+εi,i=1,2,…,T,其中μi是一维分段的恒定期望,εi~iidN(0,1),其变点个数为k,变点位置为t1,t2,…,tk.
传统的多变点估计问题首先对变点个数进行估计,得到变点个数估计后,对所有可能的变点位置组合进行搜索,选取拟合优度最好的组合作为变点的位置估计,通常利用误差平方和来衡量拟合优度[7]. 在不考虑计算复杂度的情况下,传统的多变点估计方法有较高的准确性. 但当样本量较大时,算法有可能难以实现. 对多变点估计常见的有两种解决办法:其一,利用变量选择,例如文献[8]将变点问题转化为变量选择问题;其二,利用二元分割思想[9],首先估计序列中的第一个变点,该变点将序列分为变点前后两段,再在前后两段中分别重复该过程,直至序列不可继续分段.
二元分割思想在检测多变点问题中应用广泛,在每个阶段可以看作是对单个变点的估计,执行较为简单,能同时估计出变点个数及其位置. 另一方面,BS 按照顺序每个阶段只涉及搜索单个变点,不会返回执行,这意味着BS 可能不适用于两个相邻变点之间的间距较小的情况. Fryzlewicz 指出,当任意两个相邻变点之间的最小间距大于n3/4时(n 是样本量),BS 才是有效的. 2004 年Olshen 等改进二元分割过程,提出了circular binary segmentation(CBS),称为环形二元分割[10],首先将序列的首尾连接为一个环,再对环形序列进行二元分割,并将其应用到染色体数据的异常基因组区域识别中;2014年Fryzlewicz 扩展了二元分割方法,提出了wild binary segmentation(WBS),称为野生二元分割,依据一定的随机抽取机制抽取子区间,能够改善相邻变点间距较小时无法检测的情况,使得多变点检测更具有自适应性[11]. 更多变点问题的统计研究可见参考文献[12-13].
对于正态分布的均值多变点模型,运用二元分割的思想,不断最优化每个分段的拟合优度,用最小二乘估计衡量拟合误差,将经典的最小二乘估计与二元分割思想结合,对模型中的多个变点进行估计,称其为最小二乘二元分割算法. 该改进算法不仅保持了最小二乘估计的准确性,而且能够有效估计间隔较小的两个相邻变点.
1 介绍
1.1 传统变点估计的最小二乘法
考虑离散情况的均值变点模型,Xi=μi+εi,i=1,2,…,T,假定随机误差εi独立同分布,且E(εi)=0,Var(εi)=σ2<+∞,并且有μ1=…=μk1-1=b1,μk1=…=μk2-1=b2,…,μkq=…=μn=bq+1,其中1 <k1<k2<…<kq<T. 如果bj+1≠bj,则ki就是一个变点,q 为变点个数. 具体过程如下:
第一,考虑目标函数:

此处约定k0=1,kq+1=n+1,其中令

即观察值的算数平均值,用来代替(1)式中的bj.
第二,得到如下只依赖于k1,…,kq的量

任意取一组初始值k1,…,kq,满足1 <k1<k2<…<kq<T .

第五,这样继续下去得到一组新值k′1,…,k′q,将其作为初始值,回到第二步,继续下去得到一组新值k″1,…,k″q,再回到第二步,这个过程继续下去直到无可调整时为止. 最后所得值k̂1,…,k̂q,可作为k1,…,kq的估计值.
全局遍历最小二乘中考虑变点个数q 的确定,有如下结论:式(3)中取q=1,2,…,则有T1≥T2≥…. 若只有q 个变点,则Tq与Tq+1不应相差太多. 因此,考虑两者之比Tq/Tq+1不小于1,可以设定一个略大于1的数,例如1.1,取最大的q,使Tq/Tq+1≥1.1,这个q 就是变点个数的估计.
全局遍历搜索最小二乘法对均值变点的估计较为准确,但需要预先假定变点的个数,变点个数的确定较为复杂.
1.2 二元分割方法
二元分割方法的步骤如下.
步骤1:检验无变点与单个变点,如果不存在变点,则停止;否则,估计第一个变点位置,它将整个序列分为两部分.
步骤2:分别检验这两个分段,以进行进一步细分.
步骤3:对每个分段重复该过程,直到无法进一步细分为止.
2 最小二乘二元分割
2.1 模型概述
二元分割的思想即在整段时间序列中首先找到一个变点,变点将时间序列一分为二,再在两段子序列中重复搜索过程直至结束,相当于在每段中分别找单变点. 考虑到最小二乘估计方法的准确性,故提出最小二乘二元分割方法. 考虑离散情况的均值变点模型,Xi=μi+εi,i=1,2,…,T ,假定随机误差εi独立同分布,且E(εi)=0,Var(εi)=σ2<+∞,并且有μ1=…=μk1-1=b1,μk1=…=μk2-1=b2,…,μkq=…=μn=bq+1,其中1 <k1<k2<…<kq<T . 如果bj+1≠bj,则ki就是一个变点,q 为变点个数,这里我们假定样本序列中至少有一个变点存在,即有q ≥1,考虑如下统计量

接下来讨论有无变点存在的假设检验问题,针对上述模型给出假设检验如下:

第四,将得到的变点估计b1,b2,…,bq按照其大小顺序排列后即为样本X1,…,XT的变点估计值.
2.2 阈值C 的选取
假定X1,…,XT独立同分布,有非0有限方差σ2,且有高于二阶的矩存在,对于给定的S 和S*=min{S2,…,Sn} ,当样本大小T →∞时,有以下极限定理[14]:

2.3 统计量的渐进分布
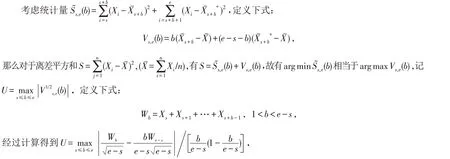
对于均值变点模型,若假定方差为1,则在不存在变点的情况下[15],有

其中:an=(2 ln lnn)12,dn=2 ln lnn+(ln ln ln n)/2.
3 随机模拟及实证分析
3.1 随机模拟
为验证最小二乘二元分割方法对正态分布多均值变点估计的有效性,利用统计软件R 进行模拟仿真,并将估计结果与二元分割方法估计进行对比. 首先生成带有四个变点的时间序列,变点位置分别为11、23、38、61,随机数据生成如下:x=c(rnorm(10,2,1),rnorm(12,3,1),rnorm(15,5,1),rnorm(23,7,1),rnorm(20,4,1)),其中得到x 的数据图如图1. 对上述随机数据重复多次实验,针对相同的数据,分别使用二元分割方法以及最小二乘二元分割方法进行估计,对比结果如表1所示.
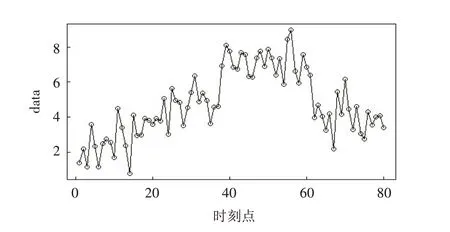
图1 模拟仿真的正态分布均值变点数据图Fig.1 Data diagram of the normal distribution mean change point

表1 传统二元分割估计值以及最小二乘二元分割估计值与真实变点的对比表Tab.1 Comparison of traditional binary segmentation estimates and least squares binary segmentation estimates with true change points
表1中b 是已知的真实变点,b̂代表两种方法的估计变点,进而 ||b-b̂ 代表真实变点与估计变点的距离,距离越小则代表估计值越准确. 由表1可以看出,最小二乘二元分割方法比传统二元分割的估计值更准确,同时在一定程度上能够减少均方误差.
另外,仿真模拟数据中共有400个变点,而传统二元分割只能检测出298个变点,低估了变点的数量,针对这一现象进行详细分析发现,当在均值变化幅度较小以及变化持续较短的情况下,传统二元分割方法无法准确地识别变点,如图2所示. 而改进的最小二乘二元分割能够较好地估计出此变点,如图3所示. 由此可见,改进的最小二乘二元分割能够在均值变化幅度较小以及变化持续较短的情况下有更稳定的估计性质.
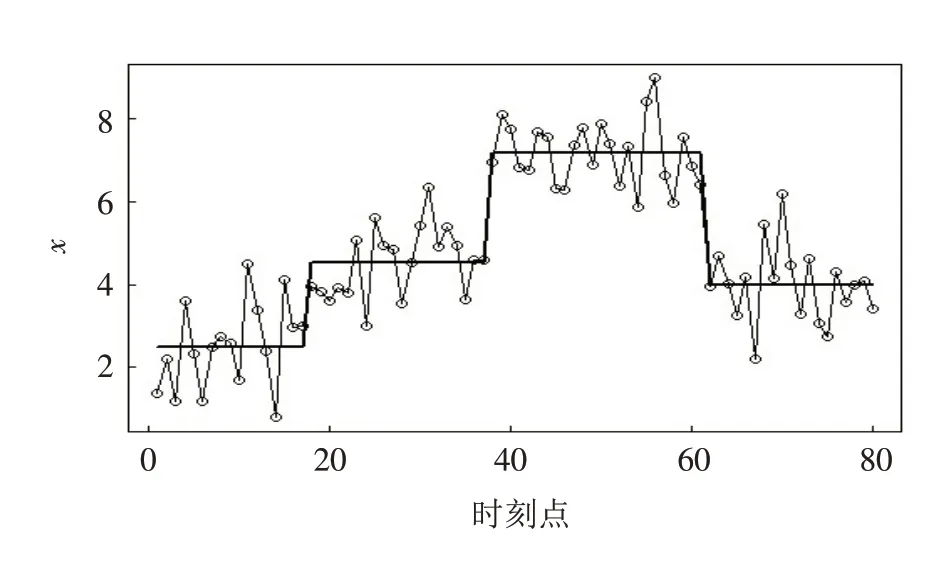
图2 传统二元分割算法得到的变点分段常数拟合图Fig.2 Variable point piecewise constant fitting graph obtained by traditional binary segmentation algorithm
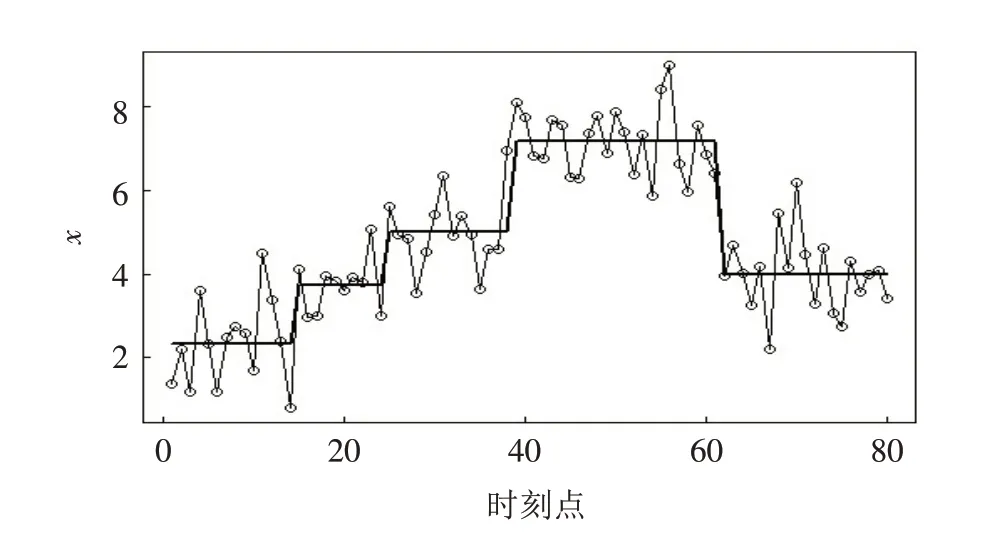
图3 最小二乘二元分割算法得到的变点分段常数拟合图Fig.3 Fitting graph of the change point piecewise constant obtained by the least squares binary segmentation algorithm
3.2 实证分析
近年来,随着社会经济的发展,人们的生活越来越富裕,出行的频率也越来越高,可供出行的公共交通也越来越多. 以火车为例,为了更好地满足旅客的出行需求,有必要对铁路客运量进行分析,研究其潜在的规律,从而能够更及时地规划部署工作. 收集到某站点一年内每天发送的旅客量数据,从历史数据中观察得出,每一年的数据有大致相同的变化规律. 旅客数量一般能够维持在平稳状态内,遇到节假日或者地域性活动时会打破该平稳状态,在该段时间内旅客数量维持另一个平稳状态,该平稳状态的持续时间与打破平稳状态的原因有关. 为了刻画此规律,选取其中一年的数据进行研究. 在整个一年数据中,工作日及周末休息日等对出行有一定的影响,因此,为了消除其对整个数据规律的影响,将全年数据分成周一到周日七个子序列,针对其中一个子序列研究其变化规律,这里选取的是周四的旅客量子序列. 将数据用散点图描述,如图4所示.
运用最小二乘二元分割方法估计变点位置,得到的变点位置估计分别为9,24,25,27,36,37,43,44,45,51. 计算得出的各分段的均值分别为:414 647,32 471,36 235,49 911,36 343,32 007,29 623,28 011,26 612,25 277,32 263. 得到的分段常数拟合图如图5所示,其中细线为旅客数量变化的折线图,粗线为使用最小二乘法计算得到的变点以及均值的分段常数拟合.
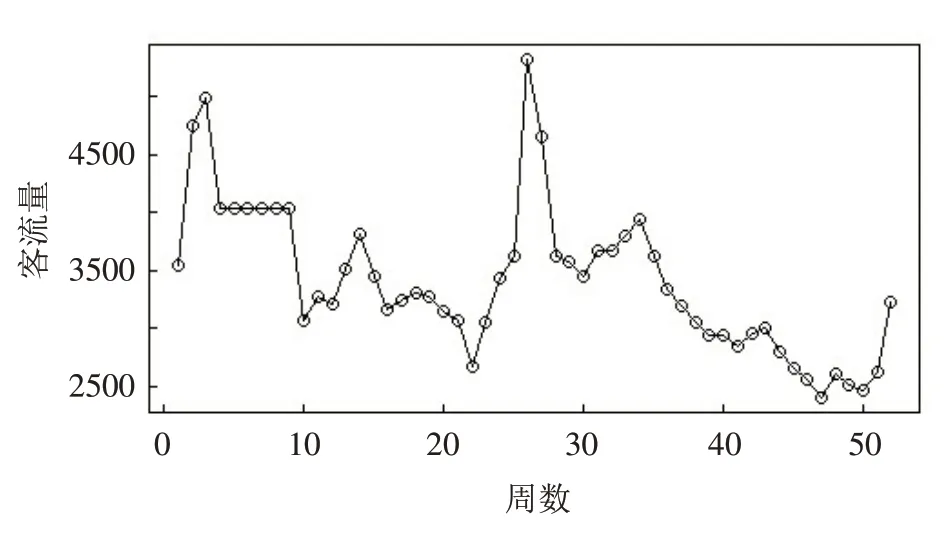
图4 某站点周四的客运量数据Fig.4 Passenger traffic data for a station on Thursday
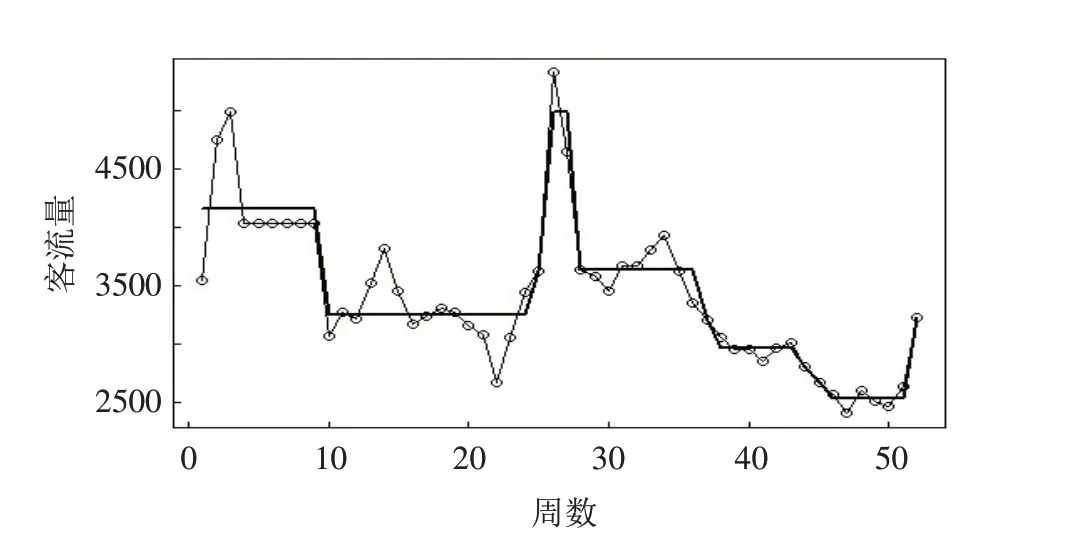
图5 最小二乘二元分割算法得到客流量分段常数拟合图Fig.5 Fitting chart of passenger flow segmentation constant obtained by the least squares binary segmentation algorithm
4 结语
大多数检测多变点的方法都是在已知变点个数的假设下估计变点位置,但是确定变点个数是比较困难的. 本文结合二元分割的思想,在不假定变点个数的情况下,实现了对变点个数以及位置的估计.
对均值多变点检测,提出了改进的二元分割最小二乘检测方法,通过模拟以及实证,验证了模型的合理性以及有效性.
基于二元分割最小二乘方法有如下结论:
1)得到了对于均值多变点模型的统计量;
2)给出了统计量的渐进分布;
3)结合实例,进一步验证该方法能更容易并且快速地同时检测出变点的个数及位置.
本文只考虑了将最小二乘与二元分割结合,在后续的研究中可以考虑将野二元分割与最小二乘相结合.
