一致性评价系数应用于无序多分类资料的效果评价
2021-10-14梁绮红陈昭宇安胜利
梁绮红,陈昭宇,张 峥,黄 爽,安胜利
1南方医科大学公共卫生学院生物统计学系,广东 广州 510515;2广州血液中心,广东 广州510095
在医学诊断实践中,通常需要用不同的测量方法或不同的评价者对测量对象的结果进行判断,对测量方法或评价者组间、组内偏差的评价称为一致性评价[1]。目前,国内外有学者提出多种方法进行一致性评价,对于无序多分类结局,1955 年提出了π index[2,3],1960 年、1968 年先后提出了Kappa 系数、加权Kappa 系数[4,5],1973年对加权Kappa系数进行扩展到多测量者的评价中[6]。然而,有研究[7]于1990年首先提出了Kappa悖论,指出其在特殊情况下存在缺陷。2008年提出的AC1系数,解决了Kappa悖论[8]的问题,具有更好的统计评价效果[9]。基于AC1系数,本课题组于2018年提出了一种针对二分类结局的一致性评价系数(CEA),其准确性、稳定性都较AC1系数高[10]。此外,已对CEA系数在三分类资料中的应用效果进行评价,但其在指定事件在总体的占比接近偶然评价率时下会产生较大偏差[11],且缺少对CEA方差的估计与置信区间的计算。目前对CEA系数在无序多分类资料的应用尚未见研究,本研究将CEA系数的应用拓展到无序多分类资料,确定其置信区间计算方法并对其应用效果进行评价,完善CEA系数在一致性评价中的应用。
1 资料和方法
1.1 常用一致性评价系数的构建
在两评价者无序多分类资料中,评价者分别为Rater A、Rater B,有k种类型,即无序多分类评价结果为1,…,k,可得列联表(表1),其中nij代表评价者A把测量对象判为i类且评价者B把测量对象判为j类的数量[12]。

表1 两评价者判别结果列联表Tab.1 Contingency table to assess agreement by two raters
一致性评价系数的构建思想是在观察一致性中扣除偶然因素的影响,进而衡量两评价者在无序多分类结局间的一致性程度[13],其基本构建公式为,其中p0为观察一致率,pe为偶然一致率。Kappa系数、AC1系数的观察一致率计算公式均为其区别在于偶然一致率pe的估计方法不同[14]。不同一致性评价系数对偶然一致率pe的定义见表2。

表2 两种一致性评价系数对pe的定义Tab.2 Definition of two consistency evaluation coefficients for pe
1.2 无序多分类CEA系数的构建
CEA系数的构建在表1中引入了偶然评价与确定评价的概念。当任意一个评价者不确定将测量对象判别到哪一类型时,称评价者做出偶然评价,反之称为确定评价。在偶然评价中,假定评价者从k个判别类型中随机等可能地选取一个判别类型作为评价结果,则把测量对象判别到正确类型的概率为1/k,即偶然正确率为1/k。只要有任意一个评价者做出偶然评价,评价者A和评价者B就会出现偶然一致性或偶然非一致性。在确定评价中,评价者A和评价者B对测量对象都做出了确定的判断,因此两评价者的判别结果将完全一致,只有确定一致性,而没有非一致性。根据两个评价者做出的偶然评价与确定评价,可得表3,其中nijCR代表评价者A做确定评价把测量对象判为i类且评价者B做偶然评价把测量对象判为j类的数量,以此类推。
假定判别类型“1”为k个判别结果中的指定事件,作以下定义:pr为指定事件在总体中的占比,即在所有事件中发生指定事件“1”的概率;ra、rb分别为评价者A、评价者B作出偶然评价的概率;pa、pb分别为评价者A、评价者B把所有测量对象判别到指定事件“1”的概率;p0为评价者A和评价者B同时把同一测量对象判别到同一类型的概率,即观察一致率,其构成包含偶然一致性与确定一致性;pe为偶然一致率;pd为偶然非一致率。

基于上述定义,由表1、表3,可得p0、pe的计算公式:
根据二分类CEA系数的构建思想[15],CEA的基本

其中,pe*为针对CEA的偶然一致率估计值,表1可由真实数据所得,因此计算CEA即可转化为求偶然一致率pe估计值的问题。
表1中的观察一致性与观察非一致性,两者均有偶然和确定两部分,即:观察一致率+观察非一致率=1、观察一致=偶然一致+确定一致、观察非一致=偶然非一致+确定非一致。对应表3,偶然一致为niiRC/RR/CR,确定一致为njjCC,偶然非一致为nijRC/RR/CR(i≠j),确定非一致为0,故有p0+pd=1。

表3 区分偶然评价和确定评价的判别结果Tab.3 Results of distinguishing the random evaluation and the certain evaluation
考虑评价者做出偶然评价的概率ra、rb,有以下关
式子可理解为:任意一个评价者做出偶然判断即为偶然评价,三种情况对应公式(4)的三部分;对于同一个观察单位,评价者A、B分别将其归到1,…,k类,则一共有k2种情况,其中A、B评价一致的情况有k种,非一致的有k2-k种,所以两评价者一致的概率为k/k2=1/k,非一致的概率为(k2-k)/k2=(k-1)/k。
评价者A、评价者B把测量对象判别到正确类的概率由确定评价和偶然评价组成。当样本量足够大时,确定评价的正确率可近似用指定事件在总体的占比pr代

因此求解pe的问题可转化为求一元二次方程f(pr)=0的解pr的问题。由于0
1.3 无序多分类CEA系数方差的估计
根据Gwet构建AC1系数的思想[7],当一致性评价推广到多个评价者时,测量者关于不同评价者的判别结果分布按表4展示,其中,r代表评价者数,n代表测量对象的样本数,rik代表把第i个测量对象判别到第k类的评价者数。本研究只考虑在两评价者的条件下推导CEA系数的方差,即r=2。

表4 按测量对象与判别类型的多评价者结果分布Tab.4 Distribution of participants and categories by multiple raters
参考Gwet使用的线性近似方法估计方差[16],通过构建一个包含所有项的样本方差去逼近真实方差,在大样本的情况下,近似方差与真实方差一致,其计算式如下:
SMA是一种骨架密实型结构混合料,经大量实践证明,SMA型结构具有优异的高温稳定性,适合用于长大纵坡路段路面施工。本文所用SMA—16型级配矿料配比如表3所示。

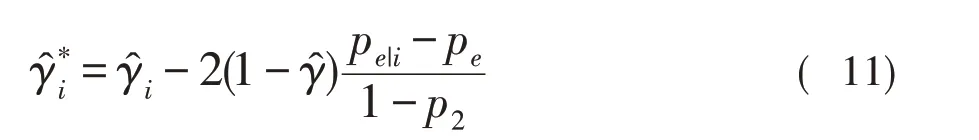
综合上述公式,样本量较大时,通过构建表4得到CEA系数方差的估计值。
1.4 无序多分类CEA系数的置信区间
Gwet在研究AC1系数方差估计与置信区间构建的文章通过模拟指出,基于上述思想构建的系数在大样本情况下具有近似正态性,因此保证了置信区间的有效性[12]。当样本量足够大时,计算出CEA系数的估计值和方差后,其95% 的置信区间即为
2 模拟与实例
2.1 模拟步骤
使用Monte Carlo模拟评价CEA系数的有效性,并对Kappa、AC1、CEA三种系数的方差估计值进行比较。模拟基于两评价者A、B,参数包括样本量n、类别数k、指定事件在总体中占比pr、两评价者的偶然评价率ra和rb。模拟步骤如下:(1)随机抽样产生一个样本量为n、包含1,…,k的数列,其中指定事件“1”的概率为pr,其余为(1-pr)/(k-1);(2)从步骤(1)中产生的数据中分两次随机抽取ra*100%、rb*100%的样本作为两评价者做出偶然评价样本,每种判别类型的概率均为1/k;(3)以含有偶然评价的样本作为原始样本,用Bootstrap法进行重抽样500次,算出每个重抽样样本的一致性评价系数及其方差。参数设置为n=20、60、100,k=3、4、5,pr=0.05~0.95(间隔0.01),ra=0.05、0.20,rb=0.05、0.20。
对CEA系数进行敏感性分析。由于CEA系数的构造与各类别所占比例有关,在实际研究,某一诊断评价中不同疾病在总体中的占比往往大不相同,即对于同一个多分类结局资料,指定事件有多种选择,其在总体的占比pr会有不同的取值,因此模拟部分探究pr在不同样本量n、不同偶然评价率(ra、rb)及不同类别数k下对CEA系数的影响。采用500次重抽样得到的一致性评价系数的均方误以评价其准确度。
对CEA系数的方差进行评价。探讨指定事件在总体的占比、偶然评价率与样本量对Kappa、AC1、CEA三种系数的影响并进行对比。采用500次重抽样得到的一致性评价系数的方差和方差的期望评价估计值的稳定性。
为了考察CEA系数的分布情况,从总体中随机抽样生成一组样本量n=50、100,类别数k=3,指定事件在总体中占比分别为pr=0.05、0.25、0.75、0.95的样本,计算相应的CEA系数。重复上述过程1000次,得到给定参数下1000个CEA系数的分布,绘制分布直方图验证CEA系数在不同样本下的渐近正态性行及置信区间的有效性。
2.2 模拟结果
由图1、2知样本量对CEA系数影响较大,样本量为60与100时CEA均方误接近,因此下述模拟中样本量分别取n=20、100(图3、4)。结果显示不同样本量下,两评价者偶然评价率不一致时(ra≠rb)的均方误都比偶然一致率相等时(ra=rb)高。当样本量较大(n=100)、偶然评价率有差异(ra≠rb)的情况下(图4),均方误随着pr的变化出现较大波动,但当pr大于0.5后,波动趋于平缓,且CEA系数的均方误始终保持在较小数值(0.005)以下。

图1 不同样本量及类别数下pr对CEA的影响Fig.1 Influence of pr on CEA under different sample sizes and type numbers(ra=rb=0.05).

图2 不同样本量及类别数下pr对CEA的影响Fig.2 Influence of pr on CEA under different sample sizes and type numbers(ra=0.05,rb=0.20).

图3 不同类别数及偶然评价率下pr对CEA的影响Fig.3 Influence of pr on CEA under different type numbers and the accidental evaluation rates(n=20).
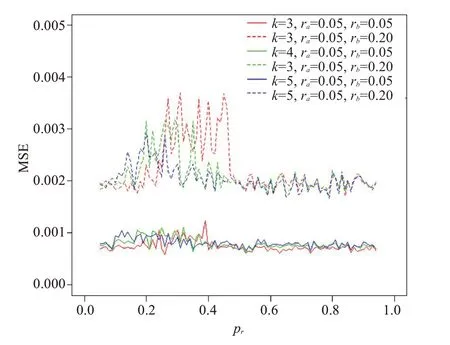
图4 不同类别数及偶然评价率下pr对CEA的影响Fig.4 Influence of pr on CEA under different type numbers and the accidental evaluation rates(n=100).
对比图5、6,两种类别数下(k=3、k=5),CEA的均方误变化情况接近,受类别数k的影响较小。样本较小(n=20)、偶然评价率不一致(ra≠rb)情况下的均方误在包括前述所有参数设置中最高。
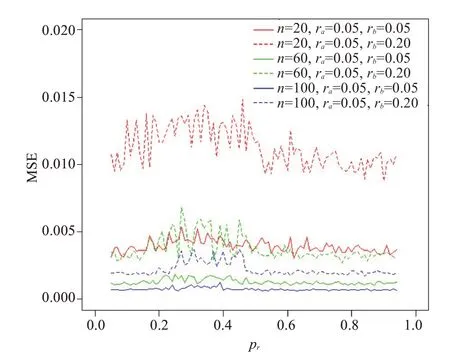
图5 不同样本量及偶然评价率下pr对CEA的影响Fig.5 Influence of pr on CEA under different sample sizes and the accidental evaluation rates(k=3).
综上,CEA系数在各种参数设置下,其均方误都保持在0.02以下,几乎不受类别数k的影响,且随着指定事件在总体占比pr的变化无明显变化趋势。偶然评价率(ra、rb)对其影响最大,样本量次之,小样本与较高的非一致偶然评价率(ra≠rb)会导致均方误较高。

图6 不同样本量及偶然评价率下pr对CEA的影响Fig.6 Influence of pr on CEA under different sample sizes and the accidental evaluation rates(k=5).
2.2.2 方差比较 参考Gwet对方差进行Monte Carlo模拟的思路[9],对CEA、AC1、Kappa进行比较,x表示三种一致性评价系数。在特定参数下,从总体中抽样所获得的一份样本,每一次重抽样都可得到一个系数的估计值xs及其方差vs(x)(s指第s次重抽样)。Var(x)表示500次重抽样所得系数的方差,即用以评价系数的波动情况,其值越小越好;E[v(x)]表示这500 次重抽样方差的期望,即(x)可通过公式(11)估计,E[v(x)]与Var(x)越接近说明方差的估计值与真实值越接近。前述结果提示类别数k对CEA系数的影响最小,因此本部分模拟全部取k=3,研究样本量n与偶然一致率(ra、rb)对方差的影响,模拟结果见表5。

表5 不同参数下各一致性评价系数的方差及方差估计值的期望Tab.5 Variance and the expectation of estimators of each consistency evaluation coefficient under different parameters(%)
上述任意一种参数设置下,CEA系数的方差均比AC1系数、Kappa系数小,Kappa系数的方差最大,且样本量越大,方差越小。三种一致性评价系数在偶然评价率不一致时(Line4~Line6、Line10~Line12)的方差均比偶然评价率一致时(Line1~Line3、Line7~Line9)高。虽然指定事件的占比处于极端值时(pr=0.05、pr=0.95),但CEA系数和AC1系数在其方差和方差的期望均不会出现较大变化,而Kappa系数在指定事件的占比较高时(pr=0.95),方差的期望则发生较大提高。随着样本量的提高,CEA系数和AC1系数方差的期望受样本量的影响不大,Kappa系数方差的期望不仅相对较前者高,且变化趋势不稳定。
综上,CEA、AC1、Kappa受偶然一致性的影响最大,样本量次之。CEA 系和AC1无论在何种情况下均比Kappa系数更加稳定。即便是在小样本的情况下,CEA的方差和方差的期望要比AC1、Kappa更接近。
2.2.3 CEA 系数的分布 固定模拟的样本量n=50、100,类别数k=3,不同pr(0.05、0.25、0.75、0.95)下随机抽样1000 次所得的CEA 系数分布直方图均服从正态分布(图略),且样本量越大,CEA 系数越趋近服从正态分布,与AC1系数的结论相同。因此用作为CEA系数95%的置信区间是有效的。
2.3 实例应用
数据来自美国国家精神健康研究所一个包含不同医生在5种精神疾病类型中对30名患者进行诊断的数据[17]。本文对数据中两名医生的诊断结果(表6)进行一致性检验,通过R软件实现一致性评价[18],参数设置为2个评价者、5分类资料。3种一致性评价方法的结果如表7,CEA系数的置信区间范围要比AC1、Kappa系数更小。

表6 两名医生诊断结果Tab.6 Result of diagnosis by two physicians

表7 3种一致性评价系数的估计结果Tab.7 Results of three consistency evaluation coefficients
3 讨论
有文献通过模拟研究比较了Kappa系数和AC1系数在无序多分类结果中的应用效果[19],得出AC1系数比Kappa系数更稳健的、受发病率影响更小的结论[20-22]。本课题组前期所提出的CEA系数也显示了较Kappa更为稳健的优势[11,15]。然而,少有研究人员使用AC1或CEA作为一致性评价方法特别是在医学领域,Kappa系数仍被普遍应用[23]。本研究完善了CEA系数在无序多分类资料中的应用,并对3种一致性评价方法进行了对比评价。
设置不同的影响一致性评价的因素:类别数k、指定事件在总体的占比pr、偶然评价率(ra、rb)和样本量n,Monte Carlo模拟研究结果显示:(1)无论何种情况,类别数对CEA系数几乎没有影响;(2)指定事件的占比在各种情况下对CEA系数影响较小,其影响程度与样本量、偶然评价率有关。当两评价者偶然评价率一致时,指定事件的影响程度较小;当样本量较小(n=30)、偶然评价率不一致时,CEA系数受指定事件的影响程度随着其占比的提高而减缓;(3)CEA系数受偶然评价率的影响相对较大,偶然评价率不一致的情况会导致CEA系数的偏差变大;(4)样本量越大,CEA系数越稳定。
对比Kappa系数、AC1系数、CEA系数的稳定性结果显示:(1)3种一致性评价系数均受样本量、偶然评价率的影响,样本量越大,系数越稳定;偶然评价率不一致会导致系数的波动程度较大,其中Kappa系数所受的影响相对其余两者要大;(2)CEA系数和AC1系数受指定事件占比pr的影响较小,而Kappa系数指定事件的占比取极端值的情况下(pr=0.05、pr=0.95)会出现方差不稳定的现象(即Kappa悖论);(3)即便是在小样本(n=30)的情况下,CEA系数的稳定性也较AC1系数、Kappa系数好。此外,CEA系数的分布接近于正态分布,其置信区间的构建是可靠性的。
综上,对于两评价者在无序多分类结局的一致性评价中,均显示本研究所提出的CEA系数具有更为稳定的特性。
本研究的前提假设是评价者在进行偶然评价时随机等可能地将观测对象判别到某一类型中,没有额外考虑评价者先验信息的影响,后续对CEA系数的改进中拟考虑诊断经验的影响。此外,本研究仅对CEA在两评价者的无序多分类结果中的应用效果进行研究评价,对于CEA系数的假设检验仍有待补充。软件实现上,Kappa系数和AC1系数在多评价者间[24]和有序多分类资料均有较多软件可以实现[25,26],包括SPSS、SAS,CEA系数在以上方面的理论推广和程序实现值得进一步完善。
