基于频率分布波形的最小跳频间隔估计算法

周德强

(装备工程技术研究实验室，河北 石家庄050081)

0 引言

目前关于跳频信号的非合作接收，主要涉及三方面的工作：跳频信号的检测、参数估计和网台分选。跳频信号的检测与参数估计主要是利用时频分析工具来检测跳频信号并估计跳频信号的频率、带宽、起跳时间、持续时间和电平等参数，主要的时频分析工具有短时傅里叶变换(STFT)[1-3]、谱图[4]、平滑伪魏格纳-威利分布(SPWVD)[5]和小波变换[6]等。文献[7-8]将阵列信号处理与时频分析结合起来，不仅能给出跳频信号的频率、带宽等参数，还能给出跳频信号的波达方向(DOA)，有助于实现跳频信号的网台分选。利用这些时频工具估计的跳频信号频率均存在一定的误差。文献[9]利用时域信号估计信号频率，计算量大，难以满足实时性要求。

网台分选可以估计出网台的数量、频率集、跳速和占空比等信息。通常利用跳频信号的参数估计结果进行网台分选，也可以直接利用时域信号进行网台分选。网台分选的主要方法有：基于起跳时间特征[10]、盲源分离[11]、支持向量聚类[12]、时频投影[13]、稀疏贝叶斯模型[14]和基于功放瞬态响应特征[15]等，这些方法普遍没有关注频率集估计的准确性。

在跳频信号参数估计精度有限的情况下，为了提高频率集估计的准确性，本文提出了一种基于频率分布波形(Frequency Distribution Waveform，FDW)的最小跳频间隔估计算法，该算法能有效估计跳频信号的最小跳频间隔，有助于网台分选中频率集的估计。

1 问题描述

跳频信号的参数估计可以给出跳频信号的频率估计值，网台分选正是利用这些频率估计值来提取频率集。

对于跳频电台，任意2个相邻信道之间的标称频率之差通常是固定的，称为信道间隔或者最小跳频间隔[16]。因此，跳频信号的频率可以表示为：

fk=f0+k*Δf，

(1)

式中，k=0，1，2，…，N-1；fk表示第k个信道的频率；N表示信道的个数；Δf表示最小跳频间隔，集合{fk，k=0，1，2，…，N-1}是网台分选中要提取的频率集。从式(1)可以看出，估计出最小跳频间隔Δf和信道频率f0就可以估计出整个频率集。

跳频信号的频率估计值可以看成频率集中频率的估计值，因此可以写成集合为：

(2)

跳频信号的频率估计值通常有一定误差，影响网台分选中频率集估计的准确性。

2 FDW算法

2.1 理论分析

设直方图统计的步长为Δt，对集合F以Δt为步长进行直方图统计，统计结果可以表示为：

(3)

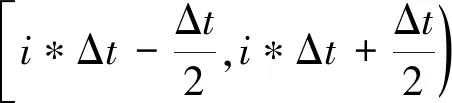
(4)

本文将频率估计值的直方图统计s(n)当作普通信号处理，因此将s(n)称为频率分布波形。为了方便理论分析，假设对每个跳频频点fk的估计值都有相同的直方图统计结果g(n)，相邻频点的估计值不交叠，则s(n)在区间[P，Q]是周期的，将s(n)平移到以n=0为起点，可以表示为：

s(n)=g(n)⊗δN(n)，

(5)

(6)

式中，⊗表示圆周卷积；C=Δf/Δt；序列s(n)的长度为M=Q-P+1=N*C；记g(n)的离散傅里叶变换(DFT)为G(k)；δN(n)的DFT为：

(7)

根据DFT的性质[17-18]，s(n)的DFT可以表示为：

(8)

从式(8)可以看出，s(n)的DFT存在等间隔分布的离散谱线，谱线的位置是：

(9)

谱线位置处的幅度是G(nk)N。最小跳频间隔Δf可以表示为：

(10)

根据式(10)，可以估计最小跳频间隔。

在实际条件下，各个跳频频点的信号数量不均匀，这导致每个频点的g(n)函数不一致，但是频率分布波形s(n)仍存在周期性的起伏，s(n)的DFT仍然有等间隔的谱线，因此仍然可以用式(10)估计最小跳频间隔。

2.2 实现步骤

在FDW算法的实现中，可以使用快速傅里叶变换(FFT)来代替DFT，以便提高计算速度。FDW算法的实现步骤如下：

① 设置直方图统计步长Δt；

② 根据频率估计值集合F构造频率分布波形s(n)；

③ 计算s(n)的FFT，得到其频谱S(k)，取 其绝对值得到|S(k)|；

④ 在|S(k)|上搜索谱线，确定其位置ni，i=0，1，…；

⑤ 将谱线幅度较高的谱线位置代入式(10)计算出若干个最小跳频间隔的估计值，这些最小跳频间隔估计值的平均值即为最终的最小跳频间隔的估计值。

2.3 性能分析

从2.1节的理论分析可以看出：FDW算法的性能取决于频率分布波形的周期性。当频率估计误差较小时，频率估计值分布比较集中，频率分布波形的周期性较好，则FDW算法的性能较好；反之，频率估计值分布比较分散，频率分布波形的周期性较差，则FDW算法的性能较差。

假设频率估计值在统计特性上是以真值为均值的高斯分布。根据高斯分布的“3σ原则”[19]：频率估计值几乎都(99.73%)在距真值±3个标准差的范围内。因此，当最小跳频间隔≥6个标准差时，相邻频点的估计值几乎不交叠，频率分布波形的周期性较好，此时FDW算法的效果较好。

综上，从理论上来说当频率估计值的标准差不超过最小跳频间隔的1/6(≈16.7%)时，FDW算法性能较好。在实际情况中，大部分频率估计值集中在真值附近，当标准差比最小跳频间隔的16.7%稍大些时，频率分布波形的周期性没有被严重破坏，FDW算法的性能恶化不明显，第3节的仿真试验验证了这一点。

3 试验验证

3.1 仿真试验

仿真参数设置：假设频率估计值在统计特性上是以真值为均值的高斯分布。跳频信号的频点数量为256，最小跳频间隔设置为25 kHz，跳频信号的频率估计值数量为5 000，直方图统计步长Δt设置为1 kHz。

3.1.1 算法验证

分别设置高斯分布的标准差为0 Hz和4 kHz，计算频率分布波形和其频谱，结果分别如图1和图2所示。从这2幅图可以看出：不管标准差是0 Hz还是4 kHz，FDW的频谱上都存在离散谱线，谱线间隔为328，FFT长度为8 192，因此最小跳频间隔的估计值=8 192/328*1 kHz=24.975 6 kHz，与真值25 kHz非常接近。从图1和图2还可以看出，当标准差较小时，FDW的频谱中存在的谱线较多且幅度较高；当标准差较大时，FDW的频谱中存在的谱线较少且幅度较低。出现这种现象的原因是：当标准差较小时，频率估计值的分布较为集中，g(n)波形“瘦且高”，其频谱G(k)衰减的比较缓慢，因此谱线幅度下降得慢；当标准差较大时，频率估计值的分布较为分散，g(n)波形“胖且矮”，其频谱G(k)衰减的比较快速，因此谱线幅度下降得快。

图1 标准差为0 Hz时的FDW及其频谱

图2 标准差为4 kHz时的FDW及其频谱

3.1.2 算法性能

当标准差太大时，频率估计值分布得特别分散，此时谱线的幅度可能很低甚至1根谱线都检测不到，这时就无法估计出最小跳频间隔，此时的估计就是失败的，因此有必要测试估计成功率与标准差的关系。均方误差代表了估计值的平均偏差，测试其与标准差的关系也很有必要。在区间[0，10 kHz]中每隔500 Hz取1个数作为待测标准差，在每个标准差下进行10 000次蒙特卡洛仿真统计成功率和均方误差，测试结果分别如图3和图4所示。从图3可以看出，当标准差不超过最小跳频间隔的18%(即4.5 kHz)时，估计的成功率可以达到100%，验证了2.3节的分析结果。

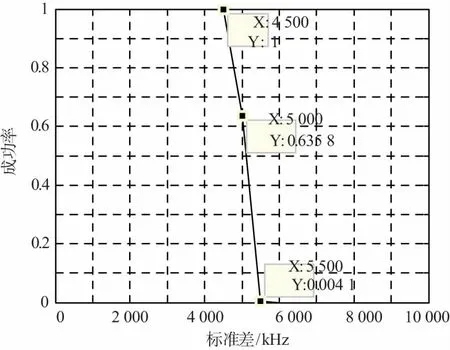
图3 不同标准差下的估计成功率

当标准差不大于4.5 kHz时估计成功率才能达到100%，因此只统计了标准差不大于4.5 kHz时最小跳频间隔估计的均方误差，结果如图4所示。从图4可以看出，随着标准差的增大，均方误差在趋势上也是增大的。当标准差等于2 kHz时，均方误差特别小，这是因为检测到的谱线数与FFT的频率分辨共同导致此时的估计值与真值特别接近。当标准差不超过最小跳频间隔的18%时，最大的均方误差为594.9，这意味着最小跳频间隔估计值与真值的平均偏差不超过24.390 6 Hz。

图4 不同标准差下最小跳频间隔估计的均方误差

3.2 实收效果

某电台信号的最小跳频间隔是150 kHz，直方图统计步长Δt设置为1 kHz，对其13 689个频率估计值的处理结果如图5所示。FDW的频谱中谱线间隔为437，FFT的长度为65 536，则最小跳频间隔的估计值=65 536/437*1 kHz=149.968 0 kHz，与真值相差32 Hz，可见FDW算法对实际的电台信号也是适用的。从图5(a)中可以看出，电台有6个同步频率出现的非常频繁，所以这6个同步频率的估计值的数量比其他频点多很多，这也导致了FDW的频谱中噪底幅度较高。如果对FDW做削峰处理，可以大大抑制噪底幅度。

4 结束语

本文提出了估计最小跳频间隔的FDW算法，推导了算法的原理，给出了算法的实现步骤，通过仿真实验测试了算法性能，验证了FDW算法对实际电台信号的适用性。当频率估计值是以真值与均值的高斯分布并且标准差不超过最小跳频间隔的18%时，FDW算法的估计成功率可以达到100%，估计的平均误差不超过25 Hz，估计精度很高，这对于网台分选中频率集的提取具有重要意义。