职初教师视角下数学师范生培养课程的实用性调查和需求分析——基于某师范大学的一项探索性研究

吴颖康，周 乐，刘 祁

职初教师视角下数学师范生培养课程的实用性调查和需求分析——基于某师范大学的一项探索性研究

吴颖康1，周 乐2，刘 祁3

（1．华东师范大学 数学科学学院，上海 200241；2．上海科学技术出版社，上海 200235；3．上海中学东校，上海 201306）

如何进行师范专业课程改革以适应教师专业化发展的需要是目前倍受关注的重要问题．从职初教师的立场出发，对其所经历的师范生培养课程进行实用性调查和需求分析能为该问题的解答提供来自一线实践者的观点．以毕业于某师范大学数学师范专业的185名职初数学教师为对象，以问卷加访谈的方式展开探索性调查，以期发现当前课程设置中存在的问题，为合理制定数学师范生培养课程方案提供建议．研究发现，这些职初数学教师认为数学类课程和数学教育类课程的实用性程度要明显高于一般教育类课程和公共课程；他们在数学教学知识、数学教学实践与技能、班级管理、大学数学与中学数学之间的联系、教师专业发展和学生心理学等方面提出了进一步的学习需求．数学师范生培养课程改革要关注课程结构的合理性，加强实践类课程建设，鼓励用教学案例联系教育理论和教学实践，加强班主任工作和学生心理学方面的课程设置，关注数学教师的“双重遗忘”现象，并充分认识教师专业的发展性要求．

师范生；培养课程；需求分析；实践性知识；专业发展

1 问题提出

百年大计，教育为本，影响教育质量的关键因素是教师．教师是一类需要特殊培养的专业人士．教师教育和专业发展的理论和实践已成为国际教师教育研究的重要话题之一．

从国家政策来看，《国家中长期教育改革和发展规划纲要（2010—2020年）》明确提出加强教师队伍建设，一系列包括中小学教师专业标准、中小学教师资格考试制度等在内的相关政策相继出台．2017年11月十九届中央全面深化改革领导小组第一次会议审议通过《全面深化新时代教师队伍建设改革的意见》，并于2018年1月印发，这是建国以来第一份以中共中央名义印发的专门加强教师队伍建设的文件．2018年3月教育部等5部门印发《教师教育振兴行动计划（2018—2022）》，指出要采取切实措施建强做优教师教育，推动教师教育改革发展，全面提升教师素质能力，努力建设一支高素质专业化创新型教师队伍．2018年10月教育部发布《关于实施卓越教师培养计划2.0的意见》，提出建设一流师范院校和一流师范专业的目标，培养造就一批教育情怀深厚、专业基础扎实、勇于创新教学、善于综合育人和具有终身学习发展能力的高素质专业化创新型中小学教师．

从师范教育的现状来看，丁钢等[1]采用分层抽样的办法调查了来自全国27所师范院校的近万名师范生后发现，师范生对于教育类课程的重视和投入程度要明显低于学科专业类课程，而用人单位认为师范生最需要提高的方面是教学技能．庞雅丽[2]通过问卷调查发现来自5所师范大学的392名数学师范生的数学专业知识要明显优于数学学科教学知识；樊靖[3]通过访谈和调查发现某师范大学数学系四年级师范生对学校数学课程知识知之甚少；闫李铮[4]发现尽管受调查的64位数学师范生能够发现学生解题中的错误，但仅有30%能深入且精准地解释错误，仅有20%能使用恰当的教学策略帮助学生改正错误．这些研究发现表明数学师范生在数学教学知识方面存在不足．这可能与中国数学师范生培养重学科轻教学、重理论轻实践的传统[5–6]有一定联系．关于数学师范生培养课程设置的已有研究普遍指出，现有课程结构有待完善，学科专业课比例过大，学科教育类课程比例较少，且缺乏实践性[7–9]．例如，基于中国21个省市区41所高校的41份数学师范生培养大纲教学计划表的文本分析，钟勇为等[10]指出数学师范专业课程体系的师范性不突出，实践教学环节不如人意．

因而，无论是从国家政策层面还是从师范教育的现状来说，师范生培养模式和课程设置面临挑战，教师教育改革势在必行．如何进行数学师范生培养课程改革以适应数学教师专业化培养和发展的需要变得尤为重要．回答该问题的一个可能的着眼点是对现有数学师范生培养课程进行实用性调查和需求分析．这与中国目前正在进行的师范类专业认证提出的构建产出导向的人才培养体系的理念相一致．有研究显示，师范生对现有培养课程的满意度不高[11]，希望加强教师职业素养、学科教材研究、课堂教学实践等方面的课程[12–14]．需要指出的是，这些研究几乎都是以在校师范生为研究对象，尚缺少基于职初教师立场和需求的研究．职初教师刚刚走上教师岗位，处于教育教学的探索阶段，势必存在着很多困惑和问题．针对这些困惑和问题有的放矢地改进师范生培养课程的设置无疑有助于职初教师更好更快地适应教学工作．

基于此，以毕业于某师范大学且工作一到两年的职初中学数学教师为研究对象，以问卷加访谈的调查方式，寻求这些数学教师对自己所经历的师范教育课程设置情况的看法，以期发现当前课程设置存在的问题，为合理制定数学师范生培养课程方案提供基于实证基础的决策依据．两个具体研究问题是：（1）职初中学数学教师认为其所经历的师范生培养课程的实用性如何？（2）职初中学数学教师对师范生培养课程有哪些从教师工作需求角度出发的内容建议？

2 研究方法

考虑到缺少职初教师视角下数学师范生培养课程设置的研究基础，将研究定位为一项探索性的研究工作，因而采用了质性研究设计，以求对研究问题给出深入的、描述性的且具有一定解释性的回答[15-16]．以某师范大学为个案，针对该校已在中学任教一至两年的数学师范毕业生，进行了基于回答开放型问题的问卷调查，并对部分毕业生进行了访谈调查．在对收集到的来自问卷和访谈的质性数据进行分析时，采用了类别建构和编码的方法，并对问卷数据的编码进行了量化统计和分析．下面详细介绍研究的对象、问卷和访谈提纲的设计，以及问卷数据的编码和分析．

2.1 研究对象

参与研究的职初中学数学教师是来自某教育部直属师范大学数学科学学院公费师范生培养项目的两届毕业生．这两届毕业生在校期间的培养方案无明显区别，具有中国数学教师培养重学科轻教学、重理论轻实践的特点[17]．这两届毕业生总计256人，其中有195人参与了问卷调查．有10份问卷由于信息不全或答题不完整被剔除，所以问卷调查的有效样本是来自全国23个省份的185位毕业一至两年的职初中学数学教师，占这两届毕业生总数的72.3%．因而，问卷调查的结果反映了大部分毕业生的看法．此外，这其中有16人接受了一对一的访谈．问卷和访谈对象的具体信息如表1所示，其中东部、中部和西部是根据地区经济水平的差异进行划分的[18]．问卷和访谈都是利用这些职初教师在暑假返回母校攻读教育硕士学位课程时进行的．

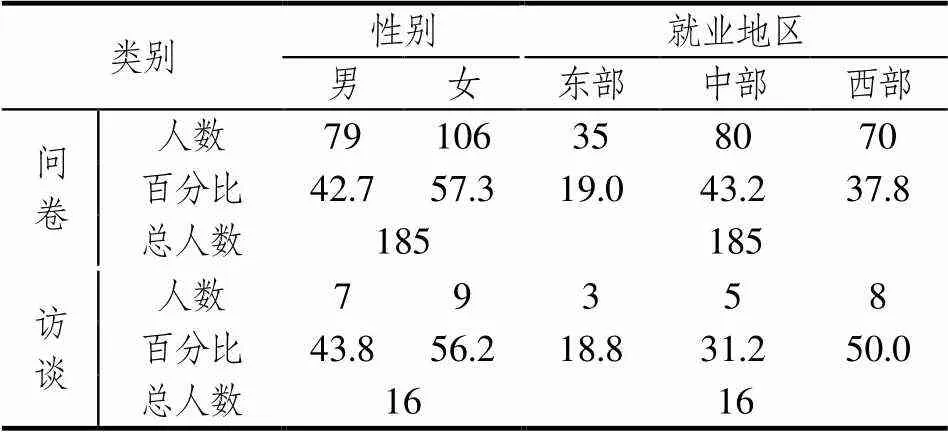
表1 研究对象的具体信息

2.2 问卷和访谈提纲设计

问卷设计简洁，除诸如性别、就业地区、任教学校等有关参与者背景信息外，只有如下所示的两道与研究问题直接相关的回答开放型问题．这两道开放题让职初教师从自身数学教学的实践经历出发反思在大学就读期间课程设置的实用性（第一问）和提出源于教师工作需求的内容建议（第二问），给予职初教师充分的自由提出个人看法，以获取更多具体信息．

请根据你这一两年的教学实践经历回答如下两个问题：（1）写出5门你认为对你做数学教师最有帮助的大学期间修读的课程名称；（2）写出你认为对你做数学教师有帮助应该在大学期间学习但没有机会修读或还需要进一步修读的学习内容．

访谈提纲包括两部分：（1）了解受访对象的基本信息，包括其任教学校的基本情况；（2）对问卷中两道问题的补充和拓展，要求受访者解释原因、给出实例、提出具体建议等．访谈时间一般在15分钟左右，最长的有半小时．所有访谈都进行了录音和转录．

2.3 问卷数据的编码和分析

问卷中两道开放题的回答需要编码处理．第一题的编码相对简单．根据这些职初教师在校期间培养方案的课程构成和他们所写的课程名称，建立了如表2所示的二级编码体系．数学类课程是指数学学科专业课程；数学教育类课程是指有关数学教育教学的理论和实践课程；一般教育类课程是指不分学科专业、作为师范生都需要修读的教育学、心理学、课堂教学管理类课程；公共课程是指以提高大学生综合素质为目的的体育类、语言类、人文艺术类、计算机类、思想政治类课程．

表2 第一问的二级编码体系

第二题编码体系的形成相对复杂，经历了两个阶段．第一阶段从理论出发，综合有关数学教师知识的理论[19-21]建立类别，但在具体编码操作中发现在这样的知识分类编码体系下有些回答（例如校本数学课程的开发等）无法归类，由此进入编码体系形成的第二阶段，即在第一阶段编码基础上根据职初教师的回答调整、增加、删减原有分类，以确保所有回答都能够归类，且所有类别都有意义，最终形成了如表3所示的二级编码体系．该编码体系包括6个一级类别，其中数学类内容领域是指大学、中学的数学知识内容以及数学知识内容的起源、发展的历史与思想；数学教学知识类是指作为一名数学教师将学术形态的数学转化为教育形态的数学所需的知识，如关于数学课程教材的知识，关于数学教学设计与教学方法策略的知识，关于数学测试与评估的知识等；数学教学实践与技能类包括实习、见习、微格培训、教学技能（教学基本功）等实践操作性活动，该类别与教学的实践性特点有关；教师专业发展类是指教师为了促进自身的专业成长所需的学习内容，包括教育研究方法、教学研究、课程开发等；班级管理类包括班主任工作和与人沟通的技巧和方法；心理学类包括学生心理学和教师心理学两方面．为确保第二题的编码体系的一致性水平，两位研究者对随机抽取的50份问卷独立编码，并进行了百分比一致性的检测，结果一致性水平达到98%．

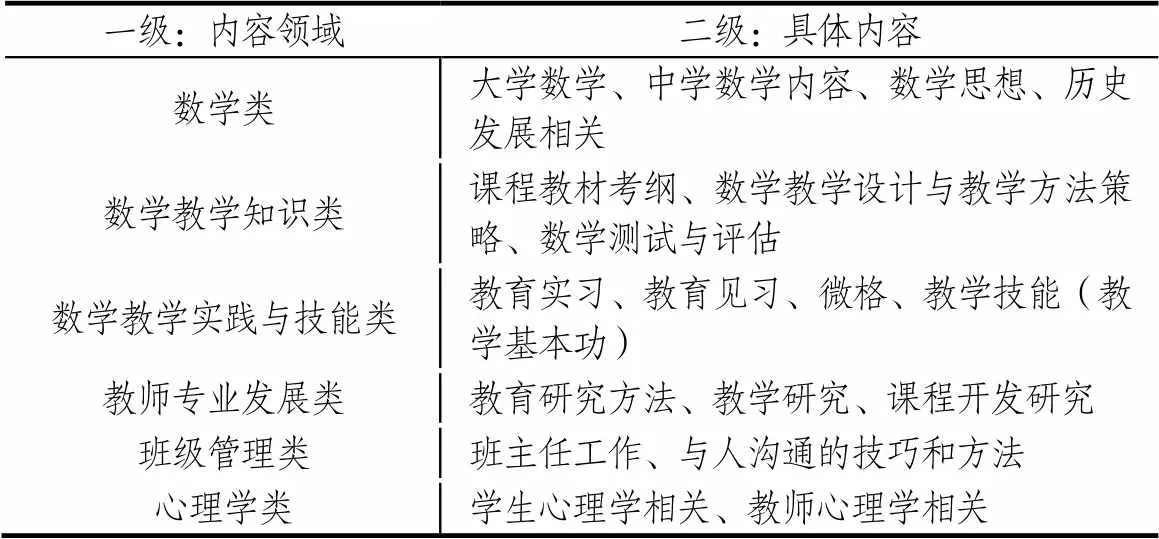
表3 第二问的二级编码体系

2.4 信度和效度

研究的信度是指“研究所得事实、数据的一致性和稳定性程度”[22]．作为一项探索性的质性研究工作，这里给出了研究对象、问卷和访谈设计、类别建立和编码过程的详细信息，有助于其他研究者进行重复研究．与此同时，在数据处理中所采用的不同编码者一致性检验也说明研究结果具有较好的可信度．

研究的效度是指“研究结果符合客观实际的程度”[22]，一般分为内部效度和外部效度．内部效度刻画了研究结果的真实程度，依赖于对研究结果的逻辑分析，而外部效度则描述了研究结果的可推广性．为保证内部效度，采用了问卷和访谈两种数据收集方式，且从这两种方式获得的数据能相互印证、融合和补充．对于外部效度，立场如下：第一，由于研究数据来源于某教育部直属师范大学的数学师范专业毕业生，所以研究发现对于同类型师范大学的数学师范专业毕业生有一定的可迁移性，但是对其他类型师范大学数学师范专业毕业生做推广时需要慎重；第二，质性研究的可推广性往往采用读者或使用者推广[23]的方式，即研究结果是否能够推广到其他人群或情境取决于读者或使用者．在这种情况下，需要提供非常具体的研究设计和研究过程的描述，以便于读者或使用者做出理智判断．按照此要求，对研究对象、研究工具的设计、数据的编码和分析、研究结果等进行了详细汇报．

3 研究结果

3.1 数学师范生培养课程的实用性分析

如表4所示，被调查的185位职初中学数学教师对师范生培养课程的实用性认识呈现出以下特征，一方面有91.9%和87.0%的职初教师认为数学类和数学教育类课程对其目前从事的数学教学工作很有帮助，另一方面仅有23.2%和15.1%的教师认为一般教育类课程和公共课程对其有帮助．

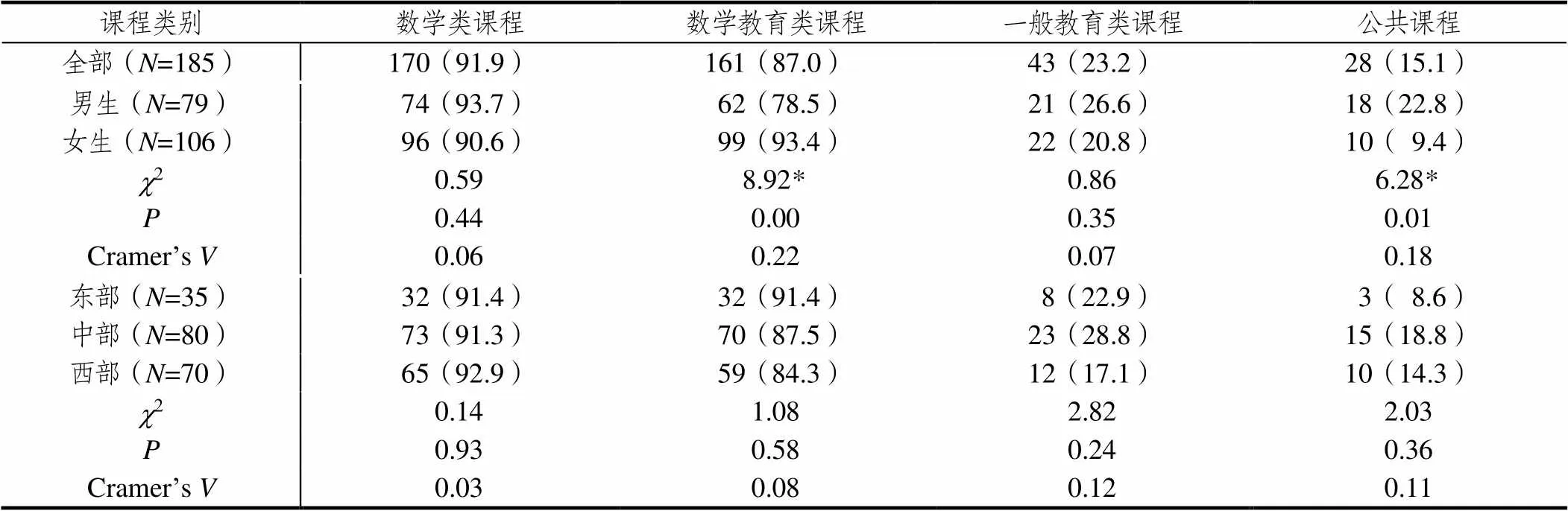
表4 职初数学教师对于4类课程实用性看法的频数分布

注：*表示卡方检验后有统计意义下的显著性差异（<0.05）

为考查职初教师对培养课程的实用性认识有无性别和就业地区的差异，进行了卡方独立性检验．结果如表4所示，职初教师对于数学教育类课程（2=8.92，=1，<0.05）和公共课程（2=6.28，=1，<0.05）的实用性认识在性别上有统计意义下的显著性差异，相比较男性职初教师，更多的女性职初教师认为数学教育类课程更为重要，公共课程并不那么重要；职初教师对于课程实用性的认识在就业地区上不存在统计意义下的显著性差异．

为考查职初教师对培养课程的实用性认识在性别和就业地区的实际显著性（practical significance），卡方独立性检验的效应量（effect size）Cramer’s显示，职初教师对课程的实用性认识在性别和就业地区上呈现弱相关[24]．尽管职初教师在数学教育类课程和公共课程的实用性认识在性别上具有统计意义上的显著性差异，但是这种差异的实际显著性较弱．

表5罗列了选择排名前十位的课程名称．同样的，高居前列的仍然是数学类课程和数学教育类课程，尤其是数学分析，有近三分之二的职初教师认为其对教学工作有帮助．这可能是因为数学类和数学教育类课程所涉及的知识内容与这些职初教师日常教学工作的关系更为紧密．例如，数学分析中的极限、导数与积分、高等代数中的矩阵与行列式、概率统计、解析几何等内容已被纳入高中数学课程，初等数论则与高中数学解题有密切联系．访谈数据则带来了更为细致的解释．例如，陕西某高中的张老师认为数学类课程有助于提升自己的数学素养和思维的严谨性，她说“数学分析等数学类课程蕴含着深刻的数学思想，例如其中的罗尔定理、拉格朗日中值定理等内容在最后阶段的高考复习中非常有帮助，虽然这些内容不必教给学生，但是教师可以在解题教学中进行渗透，因材施教”；安徽某高中的谷老师认为具有扎实数学学科基础的教师容易受到学生的尊重和认同，他说“给一些尖子生讲一些高深的数学内容，能让学生对你更加信任和崇拜，我们学校开设了校本课程，有些大学课程进入到高中，我现在开设了微积分的校本课程，给一些好学生讲一些微积分”；陕西某初中的张老师觉得数学史课程在教学中发挥了重要作用，她说“从数学史方面进行引入，学生特别喜欢，一方面故事性很强，另一方面能调动积极性，反正就是每一次只要你的这个数学课堂里面能渗透一点点关于数学史方面的小故事什么的，你就会发现那堂课的感觉真的不太一样，学生的积极性高，他们非常感兴趣”；上海某初中的曹老师持相同的观点，她认为“数学教育类课程在实际教学工作中用得到，比如几何画板比较直观，能帮助学生理解较抽象的东西，数学史课程的小故事、历史人物等能提高学生的学习兴趣和积极性”．

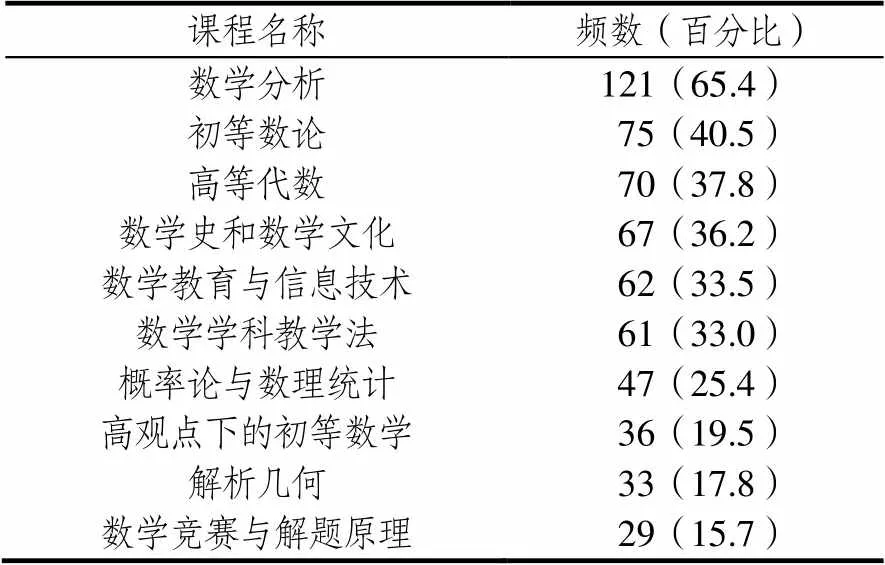
表5 排名前十位的课程名称（N=185）

3.2 数学师范生培养课程的需求分析

如表6所示，与课程实用性认识的频数分布较为集中在数学类和数学教育类课程的情况不同，这些职初中学数学教师希望修读的学习内容领域的分布相对较为分散，但也表现出一定的倾向性．根据提出人数百分比的降序排列，这些内容领域分别是：数学教学知识类（48.6%）、数学教学实践与技能类（45.4%）、班级管理类（34.1%）、数学类（18.4%）、教师专业发展类（17.3%）和心理学类（12.4%）．

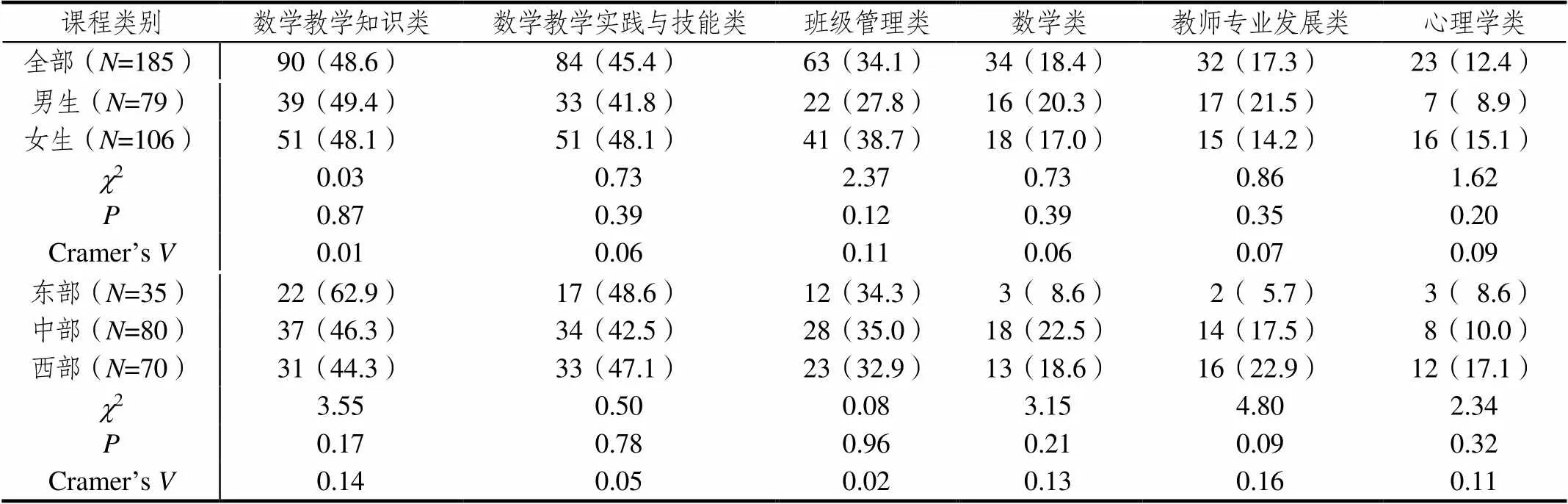
表6 职初数学教师希望修读的学习内容领域的频数分布

为考查职初教师对希望修读的学习内容领域有无性别和就业地区的区别，也对其进行了卡方独立性检验和相应的效应量计算．如表6所示，这些职初教师在数学教学知识类、数学教学实践与技能类、班级管理类、数学类、教师专业发展类和心理学类这6个大类上关于性别和就业地区均无统计意义下的显著性差异，且其实际显著性也较弱．

表7罗列了提出人数排名前十位的学习内容需求．

表7 排名前十位的内容需求（N=185）

综合表6、表7和访谈数据，对每一学习内容领域作简单阐述．有48.6%的职初教师希望加强对数学教学知识的学习，其中主要聚焦在数学教学设计与教学方法策略（70%）以及课程教材考纲（29%）这两方面．例如，来自山西某高中的杜老师建议能够多一些关于课堂教学模式方面的内容，他说“我们学校最近在学习一种新的教学模式，让学生讨论，教师基本上不讲，以学生为主体，我现在感觉比较难以把握，因为从前没有经历过，对这种新的教学模式不太适应”；来自内蒙古某初中的李老师希望能够了解并熟悉中学各个版本数学教科书的内容、编排和呈现，以更好适应入职后的教学工作；新疆某高中范老师还进一步提议在讲授数学教学知识时能结合案例进行，“因为理论听起来比较枯燥，要是结合一些案例来说的话，你就会突然间感觉到原来理论是这样用的”．

有45.4%的职初教师提及要加强数学教学实践和技能方面的培训，其中主要集中在教学技能（教学基本功）（63%）、教育实习（27%）和教育见习（23%）上．在教学技能（教学基本功）方面，许多职初教师都提及板书、语言表达、数学作图、数学软件的使用等．例如四川某高中朱老师建议强化“三字一画”的日常练习，“三字一画指黑板字、钢笔字、毛笔字和板画．如果说上课板书不好看，学生第一印象就不好，比如你刚接手一批新的学生，他们不了解你的其他地方，看老师板书，就觉得老师板书太丑了，画条直线都画歪了，画圆也画不圆这种，会有学生在下面笑”；吉林某高中顾老师特别强调数学语言的严谨性，他用函数奇偶性为例进行说明，“偶函数和奇函数的前提是定义域关于原点对称，但是用标准的数学语言来讲，应该是定义域关于原点成对称区间，数学语言表达的严谨性应该是教学基本功的一个方面”．对于教育实习和教育见习等实践类课程，职初教师希望能够有更多机会熟悉真实课堂教学，比如四川某初中周老师说，“我们现在的见习也好，实习也好，可能更多的时候是比较浅层的形式上的观摩，没有深入，没有真正了解一线教师他每天都在做些什么，他需要什么”．

班级指导是教师育人工作的重要组成，有34.1%的职初教师提到班级管理类学习内容，主要聚焦在班主任工作（92%）上．比如四川某高中朱老师说，“因为很多同学一毕业出来就要当班主任，这块要是能开设一些课的话，会对当班主任比较有帮助”．

尽管在师范生培养课程中数学专业课占了较大比例，但仍有18.4%的职初教师想要进一步修读数学类内容，主要聚焦在中学数学与大学数学的联系（71%）上．例如来自安徽某高中的顾老师说，“希望在大学期间能有教师带着整理中学数学知识内容的脉络，能站在大学数学的高度对中学数学作进一步梳理和概括”．德国数学家克莱因在其名著《高观点下的初等数学》曾提及数学教师的“双重遗忘（double discontinuity）”现象，即进入大学学习高等数学时忘记了初等数学，毕业后回到中学教书又忘记了高等数学．造成这一现象的本质原因是无法看到高等数学和初等数学之间的联系，学习好了高等数学，并不意味着就能自然而然居高临下地认识初等数学．以顾老师为代表的这些职初教师看到了这一症结所在，并提出了要加强中学数学与大学数学的联系这一学习需求．

有17.3%的职初教师提到教师专业发展方面的需求，主要集中在教学研究（63%）和教育研究方法（59%）上．比如福建某高中游老师说其就职的高中鼓励教师申报教学研究课题，但是他缺乏开展教学研究的理论知识和实践经验；上海某初中曹老师建议能介绍一些适合一线教师开展的教学研究课题；内蒙古某初中李老师说自己虽然听说过调查研究、行动研究等名词，但对其内涵和操作方式缺少了解，希望能结合具体研究课题予以介绍．

有12.4%的职初教师提到心理学类学习内容，主要聚焦在学生心理学（96%）上．比如四川某高中杨老师提议能够结合具体案例介绍学生心理学方面的相关内容，她说，“在成都有些学生心理上是有问题的，尤其是由于家庭的原因，如父母离异等，小孩会有过激性的行为，因为我刚当班主任，有时会碰到这种情况，但无从下手”；陕西省某高中张老师建议通过案例教学的方式讲授学生心理方面的理论和实践性知识，“我觉得应该拿一些现实中的中学生出现心理问题的具体实例，我们该怎么解决，就跟心理咨询师一样，教给我们沟通交流的技巧．这样不管是做知心哥哥还是知心姐姐，最起码我们能给他（她）指明正确的方向”．

4 结论和建议

4.1 结论

以毕业于某师范大学且工作一到两年的185名职初中学数学教师为研究对象，立足于其职初的教育教学工作经历，通过问卷和访谈，探索这些教师对其所经历的数学师范生培养课程的实用性认识和源于教师工作需求的内容建议．由此，有如下两个结论．

第一，参与调查的职初教师认为，数学类课程和数学教育类课程的实用性要高于一般教育类课程和公共课程．他们所列举的对其从事数学教学工作最有帮助的课程名称按频数由高到低的排名显示，位列前十的课程均为数学类和数学教育类课程，其中数学分析、初等数论、高等代数等数学类课程位居三甲，数学史与数学文化、数学教育与信息技术、数学学科教学法等数学教育类课程分别居于第四、第五和第六位．卡方独立性检验和Cramer’s效应量结果表明，这些职初教师关于数学教育类课程和公共课程的实用性认识在性别上存在统计意义上的显著性差异，但是这种差异的实际显著性较弱．

第二，这些职初教师在6个内容领域提出学习需求建议．根据提出人数百分比的降序排列，这6个内容领域分别是：数学教学知识类（主要集中在数学教学设计与教学方法策略）、数学教学实践与技能类（主要集中在教学技能即教学基本功）、班级管理类（主要集中在班主任工作）、数学类（主要集中在中学数学与大学数学的联系）、教师专业发展类（主要集中在教学研究和教育研究方法）和心理学类（主要集中在学生心理学）．卡方独立性检验和Cramer’s效应量结果表明，这些职初教师在上述六大内容领域上关于性别和就业地区均无统计意义下的显著性差异，且实际显著性也较弱．

由上述两个研究结论可见，尽管这里研究的是职初教师视角下关于某师范大学数学师范生培养课程的实用性和需求分析的探索性调查，其研究发现与现有基于在读师范生的相关研究结果有相符之处，即均指向学科教学知识和教学实践能力的加强和完善[12–14]．此外，与以在读师范生为调查对象的研究发现不同，研究中的职初教师还就班级管理、学生心理和教师专业发展的途径和方法提出学习需求建议．这说明尽管这些职初教师只有一至两年的教学工作经历，但他们对数学教师工作职责的认识已超越了“教学生学数学”，他们还认识到以学生发展为本和终身学习是教师专业的基本特征．这意味着数学师范生课程培养体系要作出相应的变革以满足上述学习需求．

4.2 关于数学师范生培养课程改革的6条建议

根据上述两个研究结论，提出关于数学师范生培养课程改革的如下6条建议．

第一，合理调整课程结构，反思不同课程类别的教育价值．比对这些职初教师所经历的师范教育课程设置和他们认为实用的课程类别，可以发现两者有明显差异．参与研究的这些职初教师在师范教育期间修读课程的总学分要求是160分，按学分递减的顺序排列依次是数学类课程（70分，43.75%）、公共课程（60分，37.5%）、数学教育类课程（17分，10.625%，其中数学学科教学法等理论课程6分，实习、见习、研习等实践类课程11分）和一般教育类课程（13分，8.125%）．数学教育类课程的学分只占到总学分要求的10.625%，但有87.0%的受调查职初教师认为这些课程对自己的教育教学工作有帮助；公共课程占总学分的37.5%，但仅有15.1%的受调查职初教师认为其实用．勒瑞彬[25]同样发现师范生课程设置结构不合理，尤其是能够体现师范性质的教师教育类课程比重偏小．研究中的发现一方面说明有必要调整师范生培养课程设置的结构以更好地满足职初教师教育教学工作的需要，另一方面也警示大家需要深刻反思公共课程和一般教育类课程的教育价值所在及应如何体现．

第二，加强实践类课程的建设．分别有48.6%和45.4%的受调查职初教师提到有关数学教学知识类和实践类方面的学习需求．该发现一方面说明这些职初教师所经历的师范生培养课程设置中数学教育类课程比例偏少的现实情况，另一方面在一定程度上也反映出数学教学知识和教学实践能力是这些职初数学教师应对数学教育教学工作所迫切需要的．目前普遍认为教师教授数学需要数学学科知识和数学教学知识，而且这两类知识相互补充，缺一不可[26]．需要注意的是，尽管许多新手教师具备了充分的数学学科知识和数学教学知识，但他们在面对课堂教学的突发问题时，往往缺乏应对，不知所措．这是因为，理论知识无法直接复制到实际教学情境中，教师的课堂教学还需要实践性知识和实践行为的支撑．中国陈向明研究团队把实践性知识界定为“教师在教育教学实践中实际使用和（或）表现出来的显性的或隐性的知识”，它既包括学术界常说的“情境知识”“案例知识”“策略知识”，也包括了教师对理论性知识的理解、解释和运用[27]．由此，数学师范生培养课程的设置除了要注重包含数学学科知识和学科教学知识在内的理论性课程之外，还一定要重视教学基本技能、见习、实习、微格教学等实践类课程，加强实践性知识的学习，为师范生提供更多（模拟）教学、反思、改进的学习机会．

第三，在教师教育类课程实施中鼓励用教学案例联系教育理论和教学实践．受调查的职初教师在访谈中提出教师教育类课程不能停留在枯燥抽象的理论讲授上，而是要结合具体的教学案例展开．事实上，课堂教学案例被认为是教师教育的核心，是沟通理论性知识和实践性知识的良好载体．随着科技的进步，课堂教学视频案例的使用日趋广泛．例如，Karsenty[28]描述了如何借助课堂教学视频案例促进中学数学教师对教学重要事件的深刻讨论和反思，文中指导教师观察、探索和反思课堂教学视频案例的框架包含6个方面：（1）与课堂教学相关的数学概念和原理；（2）教师所表现出来的明确的或隐含的教学目标；（3）课堂教学任务的设计和实施；（4）师生交互的本质特征；（5）教师在教学过程中所做的教学决策；（6）从教师的教学行为可推测出的教师关于数学、数学学习和数学教学的信念．教学视频案例一方面可以展现真实的课堂教学情境，激发教师探讨真实、丰富而复杂的教学法问题，分享和探究教学经验，达到以例识理的目的；另一方面还可以综合各种资源，有助于观摩和剖析教师的教学实践行为，因而在教师教育的课堂教学中日益受到重视，值得尝试和研究．

第四，加强班主任工作和学生心理学方面的课程设置．研究结果显示，分别有31.4%和11.9%的受调查职初教师提出班主任工作和学生心理学方面的学习需求．事实上，这两类学习需求之间具有较大的关联性．班主任区别于一般教师的核心素养包括学生发展指导能力、班级经营能力和教育沟通协调能力，这些能力的发展均建立在了解学生身心发展规律的基础上[29–30]．目前新入职教师缺乏班主任工作素养是一种较为普遍的现象，这和师范生培养中班主任方面的相关课程不到位有一定关系[31]．因此，加强师范生关于班主任和学生心理学方面的专业培训是相当必要的，一方面要帮助师范生建立以学生为本、德育为先的基本理念，另一方面也要促进师范生充分掌握学生心理发展特点和开展班主任工作的相关知识和方法，使其入职上岗后能尽快熟悉和胜任班主任的日常工作，缩短入职适应期．

第五，关注数学教师的“双重遗忘”现象，加强大学数学与中学数学的联系．数学类课程在师范生培养课程设置中所占学分比例最大，调查结果显示这些职初教师的确认为数学类课程非常重要，但仍有18.4%的受调查职初教师指出要加强数学类课程的学习，尤其是大学数学与中学数学之间的联系．这一数据在一定程度上反映出师范生培养课程中数学类课程的内容和教学有尚需改进之处．实际上，早在20年前就已经有学者[32]讨论过数学教师的“双重遗忘”现象，并提出了相应的课程改革设想．令人遗憾的是，这一问题始终存在．解决该问题的一个可能切入点是，师范大学的教师在讲授高等数学类课程时，应树立帮助师范生建立高等数学与初等数学通道的意识，并付诸于行动．例如，在近世代数的课程中，可以从群环域等代数结构的观点解读学校数学中的整数、有理数等概念及定义在其上的运算．

第六，充分认识教师专业的发展性要求．有17.3%的受调查职初教师已认识到教师这一专业的发展性，提出教师专业成长方面的学习需求，主要集中在教学研究和教育研究方法这两个方面．教师的专业成长是一个复杂的过程，其发展的本质是教学实践的改善．顾泠沅等[33]从教师课堂教学工作的构成出发提出了教师专业成长的操作模型，该模型包括目标分析、任务设计、过程测评和行为改进这4个相互关联和相互作用的要素，教师在教学实践和基于证据的反思改进中不断成长．尽管该模型针对的是在职教师的专业发展，但其基本思想即实践加基于证据的反思改进应该可以借鉴到师范生培养课程的设计和实施中，为师范生提供充分的（模拟）实践加反思的学习机会，有助于他们在提升教育教学理论知识和实践能力的同时，体会知识和能力获得的过程和方法，从而为应对走上正式的教师岗位后的教学挑战做好准备．更进一步的，在这样的学习过程中，师范生还会自发地产生如何通过收集证据改进教学实践的研究需求，此时，教育研究方法和教学研究的理论知识的介入就顺理成章、水到渠成了．

4.3 进一步研究的方向

第一，在研究的基础上开展大规模的量化倾向的调查研究，增强研究效度．以毕业于某师范大学的职初教师为研究对象，采用了问卷和访谈的数据收集方式，通过类别建构对收集到的质性数据进行了编码和分析，得到了相应的研究发现．这里的研究本质上是一项探索性的个案研究，其研究结果的可推广性具有一定的局限性．建议以研究中的发现为基础，设计以李克特量表为回答选项的问卷，开展大规模的调查研究．在样本选取时要特别注意样本的可代表性，需考虑各种类型的职初教师群体，如源于公费师范生群体的职初教师（包括返校攻读教育硕士学位和放弃教育硕士学位攻读机会的职初教师）和源于非公费师范生群体的职初教师．这样做，一方面可以进一步验证和修正研究中的发现，另一方面，由于样本量的增大，在可能的情况下，还可以进行不同类型师范大学之间和不同类型职初教师群体之间的比较和差异性检验，以期获得更为丰富和深入的研究结果．

第二，针对研究中提出的数学师范生培养课程的改革建议，有选择地设计和实施干预型研究．研究中指出了数学师范生培养课程设置中存在的一些问题，并提出了相应的改革建议，但是未对所提建议的有效性作出基于实证的验证．在进一步的研究中，需要将所提建议细化成具有可操作性的干预手段，从开展小规模的教学实验研究开始，逐步加以规模化，以诊断和检验所提建议的有效性，从而使这些建议能落到实处，发挥效用．

[1] 丁钢．中国高等师范院校师范生培养状况调查与政策分析报告[M]．上海：华东师范大学出版社，2014：10–35．

[2] 庞雅丽．职前数学教师的MKT现状及发展研究[D]．上海：华东师范大学，2011：96–112．

[3] 樊靖．高师院校数学师范生学科教学知识现状调查及研究[D]．西安：陕西师范大学，2013：15–30．

[4] 闫李铮．数学职前教师对学生错误分析与处理能力的研究[D]．西安：陕西师范大学，2014：19–29．

[5] LI S, HUANG R, SHIN H. Discipline knowledge preparation for prospective secondary mathematics teachers: An East Asian perspective [M] // SULLIVAN P, WOOD T. Knowledge and beliefs in mathematics teaching and teaching development. Rotterdam, Netherlands: Sense Publishers, 2008: 63–86.

[6] 杨玉东，李俊，高夯，等．中国教师教育与数学教师专业发展[M]．南京：江苏教育出版社，2009：176–202．

[7] 段志贵．地方高师职前教师教育课程体系的构建[D]．上海：华东师范大学，2009：37–57．

[8] 吴晴雯．高师院校数学教师教育课程体系比较研究[D]．西安：陕西师范大学，2011：31–40．

[9] 朱石焕，刘玉军．数学教师教育课程设置的思考与实践[J]．安阳师范学院学报，2014（5）：121–123．

[10] 钟勇为，林敏，宋晓平．数学师范专业课程设置调查研究——基于教学计划表的文本分析[J]．教育与教学研究，2015（7）：22–26．

[11] 滕瀚，时伟，梁支宏，等．免费师范生课程现状满意度调查分析[J]．辽宁教育研究，2008（9）：85–86．

[12] 王春梅．免费师范教育问题研究[D]．长春：东北师范大学，2009：11–25．

[13] 周晓娜．数学专业免费师范生学习现状的调查研究——以东北师范大学为个案[D]．长春：东北师范大学，2010：34–39．

[14] 黄弘毅．师范生的培养研究[D]．上海：上海师范大学，2012：26–35．

[15] JOHNSON R B, ONWUEGBUZIE A J. Mixed methods research: A research paradigm whose time has come [J]. Educational Researcher, 2004, 33 (7): 14–26.

[16] QUEIROS A, FARIA D, ALMEID F. Strengths and limitations of qualitative and quantitative research methods [J]. European Journal of Education Studies, 2017, 9 (3): 369–387.

[17]  WU Y, HUANG R. Secondary mathematics teacher preparation in China [M] // LI Y, HUANG R. How Chinese acquire and improve mathematics knowledge for teaching. Sense Publisher, 2018: 109–135.

[18] 刘忠颖．中国经济区域划分——基于各省（自治区，直辖市）人均GDP曲线的划分[D]．北京：北京师范大学，2007：3–5．

[19]  SHULMAN L. Those who understand: Knowledge growth in teaching [J]. Educational Researcher, 1986, 15 (2): 4–14.

[20]  BALL D L, THAMES M H, PHELPS G. Content knowledge for teaching: What makes it special [J]. Journal of Teacher Education, 2008 (59): 389–407.

[21] 喻平．数学教学的三种水平及其理论分析[J]．课程·教材·教法，2012，32（1）：63–69．

[22] 董奇．心理与教育研究方法[M]．北京：北京师范大学出版社，2004：124–130．

[23]  WIERSMA W, JURS S G. Research method in education: An introduction [M]. 9th ed. Boston: Pearson, 2009: 246–248.

[24]  COHEN J. Statistical power and analysis for the behavioral sciences [M]. 2nd ed. Hisdale, NJ: Lawrence Erlbaum Associates, 1988: 79–80.

[25] 靳瑞彬．六所师范院校免费师范生培养方案比较研究[D]．重庆：西南大学，2012：28–32．

[26]  ADLER J, VENKAT H. Mathematics knowledge for teaching [M] // LERMAN S. Encyclopedia of mathematics education. Dordrecht: Springer, 2014: 385–388.

[27] 陈向明．搭建实践与理论之桥——教师实践性知识研究[M]．北京：教育科学出版社，2011：58–67．

[28]  KARSENTY R. Professional development of mathematics teachers: Through the lens of the camera [R]. Regular lecture presented at the 13th International Congress on Mathematics Education (ICME-13), 2016. http://icme13.org/files/ abstracts/ICME-13-Invited-lectures-karsenty.pdf.

[29] 江涛．班主任核心素养及专业标准体系建构——基于德尔菲法的研究[J]．教育科学研究，2018（12）：78–87．

[30] 赵福江，刘京翠．我国中小学班主任工作现状问卷调查与分析[J]．教育科学研究，2018（11）：38–43．

[31] 耿申．我国中小学班主任工作现状及对策[J]．教育科学研究，2018（11）：44–50．

[32] 陈文立．关于高师数学中的“双重遗忘”问题及改革设想[J]．数学教育学报，1995，4（2）：63–66．

[33] 顾泠沅，朱连云．教师发展指导者工作的预研究报告[J]．全球教育展望，2012，41（8）：31–37，50．

Utility and Demand Analysis of Preservice Secondary Mathematics Teacher Education Curriculum from the Perspective of Novice Teachers——An Exploratory Investigation

WU Ying-kang1, ZHOU Le2, LIU Qi3

(1. School of Mathematical Sciences, East China Normal University, Shanghai 200241, China;2. Shanghai Scientific and Technical Publisher, Shanghai 200235, China;3. Shanghai East High School, Shanghai 201306, China)

How to carry out curriculum reform on preservice teacher education to meet the requirements of teacher professional development is an important current issue. One way to approach this issue is to survey new teachers who have just finished their teacher education program. This study investigated, via questionnaires and interviews, 185 secondary mathematics teachers who had graduated from a prestigious normal university in 1 or 2 years. It was found that the novice teachers highly valued courses on mathematics content and mathematics education rather than courses on general education and common courses. They also indicated a desire to learn topics such as mathematics pedagogical content knowledge, mathematics teaching practices and skills, classroom management, connections between college mathematics and school mathematics, teacher professional development, and student psychology. Preservice teacher education programs should attend to the rationality of the course structure, strengthen the learning of practical knowledge in teaching, make connections between educational theory and teaching practices via teaching cases, enhance class-advisor and student psychology-related curriculum, deal with the phenomenon of “double discontinuity,” and focus on fully understanding the developmental requirements of the teaching profession.

preservice teacher; curriculum; demand analysis; practical knowledge; professional development

G642

A

1004–9894（2021）05–0058–08

吴颖康，周乐，刘祁．职初教师视角下数学师范生培养课程的实用性调查和需求分析——基于某师范大学的一项探索性研究[J]．数学教育学报，2021，30（5）：58-65．

2021–05–07

上海市科学技术委员会资助课题——核心数学与实践（18dz2271000）；中央高校基本科研业务费项目资助；“立德树人”人文社会科学重点研究基地上海数学教育教学研究基地项目资助

吴颖康（1975—），女，上海人，副教授，博士，主要从事数学教师教育研究．

[责任编校：周学智、陈隽]