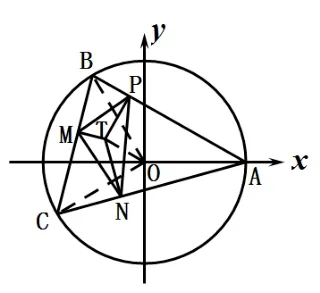
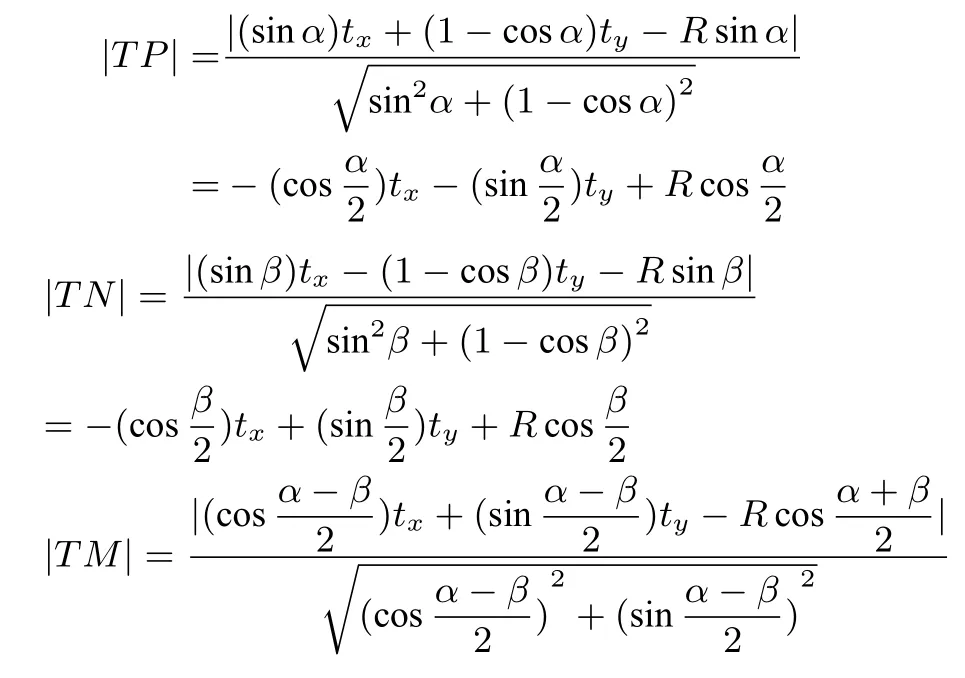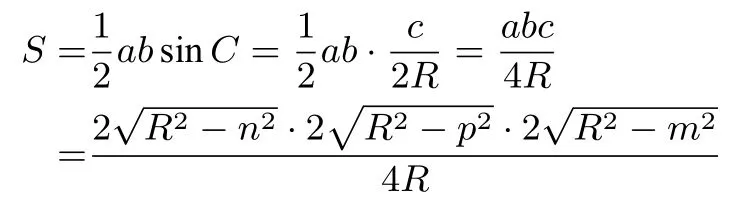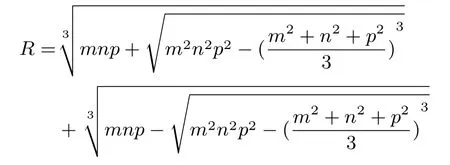一个与法尼亚诺问题相媲美的性质

广东省韶关市广东北江中学(512026) 李旭良

性质1在锐角三角形的所有内接三角形中,周长最短的三角形是其垂足三角形(锐角三角形三条高的垂足形成的三角形).(此为著名的法尼亚诺问题.)

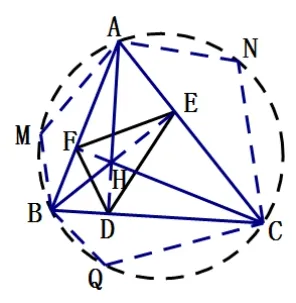
已知如图1,在锐角ΔABC中,H是垂心,ΔDEF是其垂足三角形.

图1

求证ΔDEF的周长是ΔABC所有内接三角形中最短的.

证明如图2,在BC边上任取一点D,作D关于AC、AB的轴对称点D1、D2,连接D1D2,分别交AB、AC于点F、E,于是DF=FD2,DE=ED1,从而ΔDEF的周长等于线段D1D2的长.要使ΔDEF的周长最短,就要使ΔAD2D1的边D2D1最短.由于AD2=AD=AD1,因此ΔAD2D1是等腰三角形.由轴对称性知∠D2AB=∠BAD,∠D1AC= ∠CAD,∠D2AD1= ∠D2AB+ ∠BAD+∠DAC+∠CAD1= 2(∠BAD+∠DAC) = 2∠BAC,所以等腰ΔAD2D1的顶角是固定值,腰长AD2越短,底边D2D1就越短.由此可知,AD最短时,底边D2D1就最短.因此,AD应取边BC上的高,即点D是过A作边BC的垂线的垂足.

图2

如图3,由轴对称性知∠AD2F= ∠ADF,∠AD1E=∠ADE,而∠AD2D1= ∠AD1D2,因此,∠ADF= ∠ADE.因为AD⊥BC,所以∠FDB= ∠CDE.由轴对称性知∠EDC= ∠ED1C,所以∠FDB= ∠ED1C,从而F、D、C、D1四点共圆,∠DFC、∠EFC分别是相等的弦CD与CD1所对的圆周角,所以∠DFC= ∠EFC.由轴对称性知∠DFB= ∠BFD2,因为∠D2FB= ∠AFE,所以∠DFB= ∠AFE,因为∠AFE+ ∠CFE+ ∠CFD+∠BFD=180°,所以∠AFC= ∠AFE+∠CFE=90°,所以CF⊥AB,即点F是过点C作边AB的垂线的垂足.同理,点E是过点B作边AC的垂线的垂足.因此,ΔDEF的周长是ΔABC所有内接三角形中最短的.

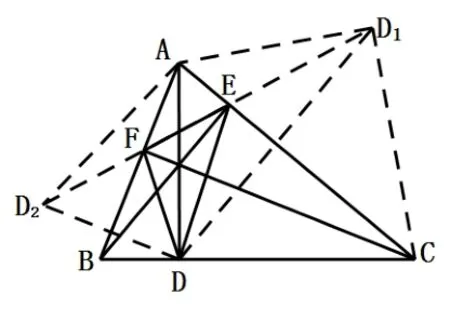
图3

现在,我们来求其周长.

若ΔABC为锐角三角形,则L0=4RsinAsinBsinC==acosA+bcosB+ccosC.

约定ΔABC的角A、B、C所对之边分别为a、b、c;垂心为H;面积为S;周长为L;外接圆半径为R.其垂足ΔDEF的周长为L0.

证明如图4,∵H为ΔABC的垂心,∴在RtΔACF中,cosA=.∵HE⊥AC,HF⊥AB,∴E、F、B、C四点共圆,∴∠AFE= ∠ACB,∠AEF= ∠ABC,∴ΔAEF∽ΔABC,,∴AE=ccosA,EF=acosA.同理ED=ccosC,FD=bcosB,因而L0=acosA+bcosB+ccosC.在ΔAEF中,运用正弦定理,,∴EF=·sinAcosA.由= 2R,得EF= 2RsinAcosA=Rsin 2A,同理,ED=Rsin 2C,FD=Rsin 2B.因而L0=R(sin 2A+sin 2B+sin 2C).

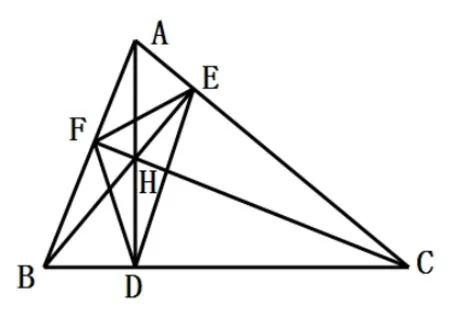
图4

从而L0= 4RsinAsinBsinC==acosA+bcosB+ccosC.

性质2若锐角三角形内一个定点到三边的距离分别为定值,则当这个定点是该三角形的外心时面积最小.

已知如图5,T为锐角ΔABC内一点,TM⊥AB于点M,TN⊥BC于点N,TP⊥AC于点P,且TM=m,TN=n,TP=p.

求证当T为ΔABC的外心时,ΔABC的面积最小.

证明(方法一) 我们约定ST表示ΔMNP的面积,O为ΔABC的外心,t表示T到O的距离.延长AT交⊙O于点Q,延长BT交⊙O于点W.∵TM⊥AB,TP⊥AC,∴B、M、T、P四点共圆,∴∠TPM= ∠WBC.同理∠TPN=∠CAQ.∵∠WAC与∠WBC是WC所对的圆周角,∴∠WAC= ∠WBC,∴∠MPN= ∠TPM+∠TPN,∠WAT= ∠WAC+∠CAQ,∴∠MPN= ∠WAT.由三角形的面积公式有

又∵BT、AT分别是四边形BMTP、ANTP外接圆的直径,∴由正弦定理,=sin ∠NAP.即

又∠AWB与∠ACB是同所对的圆周角,∴∠AWB=∠ACB.在 ΔATW中,由正弦定理有,

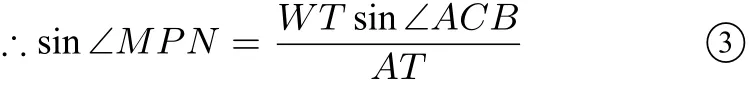
把②③式代入①式得,

又由圆幂定理有BT·WT=R2−t2(显然R>t).在ΔABC中,由正弦定理sin ∠NAP=,sin ∠MBP=S=∠ACB,于是,ST=·sin ∠ACB=(R2−t2)S.∴ST≤当且仅当t= 0时取等号,S有最小值.

图5

也就是说,锐角三角形内一个定点到三边的距离分别为定值时,这个三角形无法确定,但当这个定点是该三角形的外心时面积最小.∴当T为ΔABC的外心时,ΔABC的面积最小.

(方法二)如图6,ΔABC为锐角三角形,⊙O是它的外接圆,半径为R,设∠AOB=α,∠AOC=β(0

图6

直线AB的方程为即(sinα)x+ (1−cosα)y −Rsinα= 0.直线AC的方程为即(sinβ)x −(1−cosβ)y −Rsinβ= 0.直线BC的方程为,即= 0.而且|AB|=,|AC|=由三角形面积公式有

由点到直线的距离公式有

∵TP⊥AB,TN⊥AC,

∴T、N、A、P四点共圆,∠NTP=π−∠BAC=

同理,∠NTM=π −∠ACB=π −∠MTP=π −∠ABC=π −

④与⑤比较可知ST=当且仅当t= 0 时取等号,S有最小值.所以,当T为ΔABC的外心时,ΔABC的面积最小.

现在来求此时ΔABC的面积.如图7,因为O为ΔABC的外心,所以设OA=OB=OC=R,∠CON= ∠BON=α,∠COP=∠AOP=β,∠AOM= ∠BOM=γ.因为∠CON+∠BON+∠COP+∠AOP+∠AOM+∠BOM=360°,所以α+β+γ=180°.

图7

在RtΔCON中,cosα=

在RtΔAOP中,cosβ=

在RtΔBOM中,cosγ=

所以所以所以Rn+pm=R2n2+ 2mnpR+p2m2=R4−m2R2−p2R2+p2m2,因此R3−(m2+n2+P2)R−2mnp=0.因为−2mnp <0,所以关于R的一元三次方程只有一个正实根,运用卡尔丹公式解得:

结合三角形面积公式和正弦定理,我们有:

至此,我们得到一计算公式: 三角形的外心到三边的距离分别为m、n、p,则其面积为:S=其中

虽然这个公式有点复杂,不具备简洁性,但是有了计算公式,说明提出的问题得到有效的解决.有了计算公式就好办,尤其是借助当下先进的计算工具是可以很快求出所要的结果.

性质3若锐角三角形三个顶点到定点的距离分别为定值,则当这个定点是该三角形的垂心时面积最大.

已知如图8,H为ΔABC内一点,HA、HB、HC为定值.

图8

求证当H为ΔABC的垂足ΔDEF的内心时,ΔABC的面积最大.

证明分别以AB、BC、CA为对称轴作出点H的对称点,依次为M、Q、N,连接AM、MB、BQ、CN、NA.由轴对称性有ΔAHC∽= ΔANC,ΔAHB∽= ΔAMB,ΔBHC∽= ΔBQC,所以,AM=AN=AH,BM=BQ=BH,CQ=CN=CH.因为HA、HB、HC为定值,因此六边形AMBQCN的各边长确定.而且SAMBQCN=SΔAMB+SΔAHB+SΔBHC+SΔBQC+SΔCHA+SΔCNA=2SΔABC.

所以,当六边形AMBQCN的面积最大时,ΔABC的面积也最大.根据“边长和边的排列顺序相同的多边形中,圆内接多边形面积最大.”当六边形AMBQCN内接于圆时面积最大.由AM=AN,有∠ABM=∠ACN,而∠ABM=∠ABH,∠ACN= ∠ACH,从而∠ABH= ∠ACH.同理,∠CBH= ∠HAC,∠HAB= ∠BCH.在ΔABC中,∠ABH+∠ACH+∠CBH+∠DAC+∠HAB+∠BCH=180°,所 以,∠ABH+ ∠CBH+ ∠HAB= 90°,所 以,AH⊥BC.同理,CH⊥AB,BH⊥AC.所以,H为ΔABC的垂心.

引理三角形任一顶点到垂心的距离,等于外心到对边的距离的2 倍.

已知如图9,在ΔABC中,H为 垂心,O为外心,OM⊥AB于点M,ON⊥BC于点N,OP⊥AC于点P.

图9

求证OM=

证明分别取HA、HC的中点K、Q,连接KQ、MN.∴KQ=∵H为ΔABC的垂心,∴HA⊥BC,HC⊥AB.∵O为ΔABC的外心,OM⊥AB,ON⊥BC,∴MN=OM//HC,ON//HA.∴∠OMN= ∠HQK,∠ONM= ∠HKQ.∴ΔMON∽= ΔQHK.∴OM=HQ,ON=HK.∴OM=同理,

由引理可知,锐角三角形三个顶点到定点的距离分别为定值,当这个定点为该三角形的垂心时,那么该三角形的外心到三边的距离分别为定值.因此,性质3 与性质2 是等价的.

设三角形的垂心到三个顶点的距离分别为m、n、p,则由引理知外心到三边的距离分别为于是由性质2 的计算公式得到该三角形的面积计算公式为: