手持振动梳刷式小粒咖啡采摘装置设计与试验
2021-10-13于英杰赖庆辉贾广鑫
于英杰 王 剑 赖庆辉 贾广鑫 于 飞 曹 颖
(昆明理工大学农业与食品学院, 昆明 650500)
0 引言
小粒咖啡(CoffeaarabicaL.)又称为云南小粒咖啡。2017年云南省咖啡种植面积11.8万hm2,咖啡生豆产量13.6万t,均占全国的98%[1-2]。采收是小粒咖啡生产的关键环节,传统的人工采收成本高、效率低,严重制约小粒咖啡产业的发展。因此,研究小粒咖啡采收机理并设计一款适合丘陵山区小粒咖啡收获的机器很有必要。
国外关于咖啡机械化收获的研究较早,巴西、哥伦比亚等地势平坦的咖啡产区,多使用骑垄梳刷式或侧牵引梳刷式大型机械进行咖啡采收[3-6],但这种采收方式不适合云南小粒咖啡海拔高、坡地多的种植环境,国内关于小粒咖啡采收技术及机器的研究鲜有报道。咖啡属浆果类果实,针对浆果类收获的采摘机大致可以分为气力式、连续式、撞击式和梳刷式4种[7]。气力式采摘机主要用来采收柑橘等大果实,且运行成本高、能量损失严重;连续式和撞击式采用特殊的振动机构夹持树干或树枝进行果实采摘,最高采净率超过90%[8-15],采摘机多为大型机械,作业空间要求高且价格昂贵,不适合小粒咖啡的收获。国内研究人员对黑加仑、葡萄、枸杞、蓝莓等小浆果类进行了便携式采摘机的研究,便携式采摘机的工作方式多以振动式为主,振动形式包括偏心连杆式、曲柄滑块式以及气力振动式等[16-19]。振动式采摘机与果树存在刚性接触,会对果树造成一定的物理损伤。虽然梳刷式采摘机收获效率取决于果园的规范化种植条件,但是与连续式、撞击式收获机相比,梳刷式收获机与果树柔性接触,收获过程中对果树造成损伤较小,近些年得到广泛研究[20-22],但是小粒咖啡果实成熟期不同且结合力较大,这些装置很难满足成熟小粒咖啡的有效采摘。
为此,本文设计一款手持振动梳刷式小粒咖啡采摘机,通过建立小粒咖啡果实-果柄力学模型,分析得到果实脱离果柄的条件,通过建立果树-机械动力学模型与ADAMS仿真试验,确定采摘机的结构参数和工作参数,最后通过田间试验对采摘机的工作性能进行验证,为实现小粒咖啡的机械化收获提供理论依据。
1 整机结构与果实脱落力学特性分析
1.1 整机结构与工作原理
手持振动梳刷式小粒咖啡采摘装置主要由振动部件和梳刷部件组成,具体结构如图1所示。振动部件包括凸轮轴、传动轴、链轮、链条、调节板、固定壳体、偏心轮等;梳刷部件包括梳齿、梳齿卡扣、指排光轴等。
作业时,手持外壳把手启动电源,由直流电机通过链传动带动偏心块相向转动,偏心块产生的相对运动惯性力带动整机做间歇性回转运动,牵连运动惯性力带动整机做整体转动,将小粒咖啡果树枝条置于相邻两指排之间,然后沿着枝条方向移动,枝条在指排的作用下产生一定振幅和频率的晃动,同时指排在转动过程中会拍打果实,当小粒咖啡果实-果柄连接处受到的作用力大于两者之间的结合力时,果实从果柄处脱落,从而实现收获。
1.2 小粒咖啡果实脱落力学特性分析
为建立准确的小粒咖啡“果实-果柄”力学模型,对小粒咖啡实际生长情况进行了调研,咖啡枝条上长有10~12个节点,咖啡果呈簇状分布在每个节点上且果柄较短,如图2a所示,可以将果实-果柄简化为悬挂点移动的单摆模型进行研究[23]。
小粒咖啡果实单摆受力情况如图2b所示,以果实中心为原点O建立坐标系,振动部件产生的作用力统一为惯性力,在单摆模型中简化为拉力FL。FL可分解为法向拉力Fn和切向拉力Ft,咖啡果实产生的加速度a分解为法向加速度an和切向加速度at,则有
(1)
式中m1——小粒咖啡单果质量,kg
ψ——咖啡果转动的角位移,rad
l——果柄长度,m
t——作业时间,s
r0——咖啡果实长轴半径,m
小粒咖啡的脱落形式主要有两种:在法向拉力Fn作用下,在果柄与果实结合处断裂;在切向拉力Ft的作用下,果柄断裂[24]。由于小粒咖啡属于呼吸跃变型果实,保存时间很短,在果柄-果实结合处断裂的小粒咖啡果实质量高且可避免二次筛选,因此收获的判定条件定为果实从果实-果柄结合处发生断裂,即满足
FG (2) 式中FG——果实-果柄结合力,N β——重力G与Fn的夹角,(°) G——果实重力,N 在单摆模型中咖啡果实以点P为中心摆动,则咖啡果转动的角位移ψ为 (3) 式中A——果实受迫振动振幅,mm ω——偏心块角速度,rad/s 收获过程中产生的拉力FL远大于小粒咖啡果实的重力G,因此果实重力可忽略不计,所以咖啡果实在果柄与果实结合处断裂,需满足 (4) 从而确定实现咖啡果实收获所需的力FL为 (5) 果树-机械收获模型如图3所示,在水平面上,以振动机构梳刷杆中心O为原点建立直角坐标系,振动机构绕着原点运动,该收获模型可简化为双自由度“质量-弹簧-阻尼”收获系统,采摘机梳齿与果树柔性接触,树枝、梳齿固有特性采用等效阻尼系数和弹性系数表示[15,25]。 首先确定果树-机械收获模型所存在的力,列出其微分方程,然后根据达朗贝尔原理(动静法)求解得出振幅稳态响应表达式。 运动过程中偏心块的绝对运动惯性力由相对运动惯性力及牵连运动惯性力组成。 相对运动惯性力方程为 (6) 式中F1x、F1y——偏心块绕轴线转动在x、y方向产生的惯性力,N m0——偏心块质量,kg r——偏心块的转动半径,m φ0——合成惯性力与水平面夹角,(°) 牵连运动惯性力方程为 (7) 式中F2x、F2y——偏心块轴线随整个振动机构振动在x、y方向产生的惯性力,N 采摘机惯性力方程为 (8) 式中Fmx、Fmy——采摘机x、y方向惯性力,N m——整个振动部件除偏心块的质量,kg 梳齿弹性力、阻尼力方程分别为 (9) (10) 式中Fkx、Fky——梳齿在x、y方向弹性力,N Fcx、Fcy——梳齿x、y方向阻尼力,N k——梳齿等效弹性系数,常数 c——梳齿等效阻尼系数,常数 树枝惯性力、弹性力、阻尼力方程分别为 (11) (12) (13) 式中Fm′x、Fm′y——树枝在x、y方向惯性力 m2——作用树枝的等效质量,kg Fk′x、Fk′y——树枝在x、y方向弹性力,N Fc′x、Fc′y——树枝在x、y方向阻尼力,N k′——树枝等效弹性系数,常数 c′——树枝等效阻尼系数,常数 根据达朗贝尔原理,采摘机工作时,各作用力相互平衡,瞬时合力为零,据此建立整个系统在x方向、y方向的微分方程为 (14) (15) 其中 M=2m0+m+m2 式中M——整个系统质量,kg 根据振动力学理论,指排轴随着振动部件做简谐运动,因此整个系统的振动响应是简谐函数,其x、y方向位移为 (16) 式中Ax、Ay——简谐运动下x、y方向振幅,mm γx、γy——x、y方向激振力对位移的相位差角,(°) 将简谐运动的位移、速度和加速度代入式(14)、(15)得 -MAxω2sin(ωt-γx)+(k+k′)Axsin(ωt-γx)+ (17) -MAyω2cos(ωt-γy)+(k+k′)Aycos(ωt-γx)- (18) 求得系统在x方向振幅和相位差角的稳态响应表达式为 (19) (20) 同理可得y方向稳态响应的振幅和相位差角表达式为 (21) (22) 2.2.1偏心块 偏心块是振动部件主要组成部分,常见的偏心块主要有半圆式、过半圆式、少半圆式和重锤式4种型式。通过理论计算及建模分析可知,同规格半圆式偏心块与其他3种型式的偏心块相比产生的惯性力最大。此外,偏心块分为带圆角和不带圆角两种,带圆角偏心块的最大总变形及最大等效应力优于不带圆角偏心块,因此选用半圆式带圆角偏心块。 在振动过程中振动部件的弹性力及阻尼力远小于其产生的激振力,因此在偏心块设计时将机体产生的激振力近似等于小粒咖啡果实结合力,据此逆向推导,从而确定偏心块的最佳尺寸。在云南省普洱市小粒咖啡试验田调研时,利用SF-20型数显式推拉力计对50个成熟小粒咖啡果实样本的结合力进行测定,测得熟果期小粒咖啡果实结合力范围为5.25~7.16 N。为满足收获条件,根据半圆式偏心块计算理论[26],确定偏心块大外圆半径R为100 mm,小外圆半径r1为12.5 mm,内圆半径r2为6 mm,厚度为20 mm,材料选择45钢,质量为0.6 kg,偏心距为29 mm。 2.2.2梳刷部件 振动梳刷式小粒咖啡采摘机在收获过程中梳齿与小粒咖啡果实和枝条直接接触。梳刷部件的设计与分布由小粒咖啡树形参数决定。 咖啡果树枝条长度400~500 mm,单节点果实挂果幅宽20~30 mm,为确保梳刷效率,保证指排转动一圈可碰到同根枝条上所有咖啡果,确定梳齿长度100 mm,梳齿直径6 mm,呈60°分布,通过梳齿卡扣固定在指排光轴上,便于更换。合适的指排间距是高效收获小粒咖啡果实的关键,间距过小,容易损坏果实和枝条,影响收获品质及产量,间距过大,则不能有效收获果实,影响收获效率。因此,梳齿卡扣通过顶丝固定在带键槽的光轴上,通过调节梳齿卡扣在指排光轴上的位置来控制指排间距,通过预试验及仿真试验确定指排间距为20~40 mm。 梳齿材料影响小粒咖啡的采收效果,选择3种材料的梳齿进行预试验,分别为不锈钢、ABS和橡胶。在预试验中选择一致的工作参数,结果表明:不锈钢棒材采净率最高,ABS棒材次之,橡胶棒材采净率最低,但是不锈钢棒材损伤率明显高于ABS棒材和橡胶棒材,综合考虑,选择ABS棒材作为梳齿材料。 2.2.3调幅机构 如图4a所示,设初始状态两偏心块夹角为θ,根据平行四边形定则确定合力方向,合力与x轴夹角为φ0。在0°~90°范围内,随着θ增大,φ0逐渐减小。由式(19)、(21)可知,振动部件产生的振幅会随着φ0的改变而改变,因此可通过改变偏心块夹角来改变振幅。 调幅装置示意图如图4b所示,其主要由调节板和固定壳体组成,带槽轴承固定在调节板上,在固定壳体上设有长孔,在调节板上有焊接螺母,通过调节螺栓改变调节板在固定壳体上的位置来实现拉紧和放松,调整好偏心块角度后,在3个长孔上用螺栓固定。 为建立合理准确的果树-机械仿真模型,在云南省普洱市云南农业大学热带作物学院的咖啡试验区对树龄为4 a的“卡蒂姆”品种小粒咖啡果树的物理力学特性参数进行了测量,具体的测量方法如下:用卷尺、游标卡尺、角度测量仪等对小粒咖啡果树的枝条长度、枝条直径、果柄长度、节点数、单节点挂果数等进行测量。采用SF-20型数显式推拉力计对不同成熟度的小粒咖啡果实结合力进行了测量。每个成熟度各取50个样本,为方便统计数量,每个测试结果四舍五入取整,统计结果如图5所示,从而确定不同成熟度果实结合力范围,如表1所示。此外,采集试验样本,用TA Type-XTPlus型质构仪、JA5103型高精度电子秤(精度为0.001 g)和量筒对小粒咖啡树枝及果柄的密度、弹性模量等进行测量。采用五点取样法取10棵果树作为试验样本,每项参数测量20组,得到20组试验数据后进行统计分析,结果如表2所示。 表1 不同成熟度果实结合力范围Tab.1 Fruit binding capacity range of different maturities N 表2 云南小粒咖啡果树树形参数Tab.2 Tree shape parameters of Coffea arabica L. 应用ADAMS建立果树-机械刚柔耦合模型,仿真模型如图6所示。首先,根据表2中数据利用NX三维软件对小粒咖啡进行建模,由于建立柔性体果树需要将果柄和枝条离散化,因此将果实、果柄、树枝分别建模,再进行装配。然后,对振动梳刷式小粒咖啡采摘机进行建模,为减少运算量,加快运行速度,尽可能简化整个机构模型;最后,将果树模型和采摘机模型置于合理位置装配,将装配好的模型转换成x_t格式导入ADAMS进行设置,得到完整的果树-机械刚柔耦合模型[27]。 3.2.1最佳摩擦阻力确定 在采摘机设计过程中发现,电机通过链传动带动偏心轮转动时,受扭矩和摩擦的影响会导致偏心轮不转而整个振动机构在壳体里转动,因此,增加了阻力调节器,其中刹车与刹车片的阻尼系数为0.45 N·s/mm、弯曲作用力臂为110 mm、刚度系数为2 145 N/mm、静摩擦因数0.05、动摩擦因数0.03[28]。为分析不同刹车阻力对激振力和频率的影响,利用ADAMS进行了仿真试验。 将简化后的采摘机模型和单个果柄-果实模型导入ADAMS/View中,并给采摘机添加约束和驱动。将单个带果柄的小粒咖啡果实置于两梳齿之间,果柄一端与ground 固定连接,一端与果实采用弹簧阻尼模型连接;利用ADAMS/AutoFlex模块,将果柄刚体转换为柔性体,模数设为6,并创建新的果柄材料,如表3所示;将梳齿与卡扣固定连接后,用同样的方式将梳齿转化为柔性体;仿真过程中不考虑小粒咖啡果实的损伤,所以将咖啡果实视为刚体,在果实与梳齿之间创建接触力,接触类型选择柔性体对刚体。利用扭矩传感器(DYN-200型)测得电机通过主轴带动两个偏心块转动的扭矩为0.46 N·m,刹车圆盘直径为220 mm,因此摩擦力至少为4.18 N。仿真时,设定两偏心块角速度为30 rad/s,在相同转速的情况下,不同刹车阻力对采收机激振力和激振频率的影响结果如图7所示。 表3 柔性体材料属性参数Tab.3 Flexible body material attribute 由图7可知,当摩擦阻力为4.2 N时,激振力主要分布在50 N左右;当摩擦阻力为8.2 N时,激振力主要分布在30 N左右。随着摩擦阻力的增大,采收机的激振力在不断减小。因此,在确保两偏心块转动的情况下,摩擦阻力越小越好,所以将摩擦阻力定为4.2 N。 3.2.2偏心块夹角对振幅影响分析 为确定不同偏心块夹角时的平均振幅,将简化后的采摘机模型导入ADAMS中,角速度设定为10 rad/s,添加连接和驱动后对不同角度下平均振幅进行了仿真,结果如图8所示。 从图8可看出,工作过程中,梳齿随着振动部件做简谐运动,改变两个偏心块之间夹角后,梳齿的运动轨迹不会发生太大的变化,其振幅发生了改变,通过对仿真结果的分析计算可知:偏心块夹角在0°~90°之间变化时,平均振幅先减小后增大。夹角为0°时平均振幅最大,可以达到10 mm;夹角为45°时平均振幅最小,为6 mm;夹角为90°时平均振幅为9 mm。 为确定梳刷式小粒咖啡采摘机正交试验影响因素及水平,依据现有研究成果[20-21],选取频率、偏心块夹角、梳齿间距作为试验因素;通过预试验,定义各试验因素的固定值为25 Hz、22.5°、30 mm。以收获咖啡果数作为试验指标,固定两个因素,研究另一因素对试验指标的影响规律,进行单因素仿真试验。 3.3.1参数化模型建立 收获过程中将果树枝条简化为悬臂梁结构,将枝条一端固定在ground上,采用离散法建立咖啡果柄和咖啡枝条柔性体,将枝条实体离散成圆台,各圆台采用BUSH连接。仿真试验采用广义力与传感器函数控制的思路,可在梳刷收获过程中对多个独立的小粒咖啡果实脱落仿真过程进行检测控制[25,29]。仿真时在果柄与枝条之间添加弹簧阻尼模型,在果柄与果实之间采用广义力连接,广义力由3个分量力和3个分量力矩(Fx、Fy、Fz、Tx、Ty、Tz)组成。利用传感器检测果实与果柄间广义力的变化,当检测到广义力达到咖啡果实脱落的最小值时,广义力突变为零,判定咖啡果实与果柄脱落,实现收获。由上文可知,小粒咖啡熟果最小结合力为5.45 N,结合力刚度K为360 N/m,阻尼系数C采用默认值。 梳刷收获过程中咖啡果实受力很复杂,所以在咖啡果实与果实之间、果实与梳齿之间、果柄与梳齿、枝条与梳齿之间添加接触力,最后给采摘机添加连接和驱动,进行仿真。 3.3.2不同频率对果实脱落的影响 由图9a可知,随着振动频率的增加,收获小粒咖啡果实总量逐渐增加,单位时间内果实脱落数量也逐渐增加,因为频率越高,要求电机转速越大,产生的激振力就越大,果实受到的惯性力也就越大,且碰撞次数增多,果实更容易脱落。当频率为10 Hz时,收获效率相对较低,且最终果实脱落数量也少,当频率为40 Hz时,收获效率和最终果实脱落量与30 Hz相差无异。因此选定频率水平范围为20~30 Hz。 3.3.3不同梳齿间距对果实脱落的影响 由图9b可知,随着梳齿间距的不断减小,收获小粒咖啡果实的数量和速度都逐渐增加。这是由于梳齿间距越小,在振动梳刷过程中与咖啡果的有效碰撞增加,但是梳齿间距过小会增加果实破损率。因此选定梳齿间距水平范围为20~40 mm。 3.3.4不同偏心块夹角对果实脱落的影响 由图9c可知,随着偏心块夹角的减小,果实脱落数曲线向左移动,表明果实脱落时间减小,主要因为偏心块夹角减小,振动装置振幅增大,咖啡果所受的惯性力也增大。但是当偏心块夹角从9°减小到0°过程中,果实脱落数曲线基本重合。因此选定偏心块夹角范围为0°~45°。 为获取小粒咖啡收获时频率、梳齿间距和偏心块夹角的最佳组合参数,2020年11月,在云南省普洱市云南农业大学热带作物学院的小粒咖啡试验田进行了田间试验,试验品种为树龄4 a的“卡蒂姆”小粒咖啡。样机试验如图10所示。 采用二次回归正交旋转组合试验设计,以频率、梳齿间距和偏心块夹角为试验因素,以采净率η1、采青率η2和损伤率η3为试验指标,进行试验设计。通过仿真试验可知频率范围为20~30 Hz,对应电机转速720~1 020 r/min;梳齿间距范围30~50 mm;偏心块夹角范围0°~45°。 为确保试验效果,试验时将电机调到所需转速稳定后再将咖啡枝条放入指排之间,收获时间为15 s。采用三因素五水平二次回归正交旋转组合试验,共进行23组试验,每组试验进行3次,取3次试验的平均值作为该组试验的测试结果,试验因素编码如表4所示。 表4 试验因素编码Tab.4 Horizontal coding of experiment factors 根据表5中所得到的试验数据(X1、X2、X3为因素编码值),利用Design-Expert 8.0.6对试验结果进行了多元回归拟合,由表6可知,采净率的回归模型(P<0.000 1)、采青率的回归模型(P<0.000 1)和损伤率的回归模型(P<0.000 1)均极显著,回归方程有意义,并且采净率、采青率和损伤率的拟合方差均不显著,说明回归方程拟合很好。剔除回归模型中的不显著影响因素(P>0.05)后,得到采净率Y1、采青率Y2和损伤率Y3的回归方程 (23) (24) (25) 从表6可知,各因素对采净率的影响重要性依次为频率、梳齿间距、偏心块夹角,其中频率与梳齿间距的交互作用不容忽视,二者响应曲面如图11a所示。随着频率增加且梳齿间距减小,采净率提高,当频率和梳齿间距达到一定水平时,其采净率的增加趋势趋于平缓。频率越高,要求电机转速越大,产生的激振力就越大,果实受到的惯性力也就越大,采净率越高。梳齿间距越小,梳齿与果实的有效接触越多,采净率越高,尤其在采收后期当一根枝条上的果实不多时,小的梳齿间距更容易实现收获。 各因素对采青率的影响重要性依次为频率、梳齿间距、偏心块夹角,其中频率与梳齿间距的交互作用不容忽视,二者响应曲面如图11b所示。随着频率增加且梳齿间距减小,采青率逐渐升高,并且采青率增速越来越大。 表5 试验方案与结果Tab.5 Experiment design and results 表6 方差分析Tab.6 Analysis of variance 各因素对损伤率影响重要性依次为梳齿间距、频率、偏心块夹角,其中频率与梳齿间距的交互作用不容忽视,二者响应曲面如图11c所示。随着频率增加且梳齿间距减小,损伤率逐渐升高,主要因为小粒咖啡生长较密,果实与果实之间、果实与主干之间存在作用力,在梳刷过程中,当梳齿间距过小而产生激振力又不足以使果实从果柄处断裂时,果实与果实、树干及梳齿之间会产生一定的摩擦与挤压,容易造成果实破皮及果柄非正常断裂等现象。 设定采净率大于90%,采青率小于10%,损伤率小于5%,优化所得最佳参数范围如图12所示,在偏心块夹角为22.5°时,黄色区域为参数优化区域,即频率为24.67~27.49 Hz,梳齿间距为28.5~35.16 mm时,采净率大于90%,采青率小于10%,损伤率小于5%。 对优化后的结果进行试验验证,在相同的试验条件下选取偏心块夹角22.5°、频率26 Hz、梳齿间距32 mm,进行3次重复试验,得到采净率均值为91.35%,采青率均值为8.46%,损伤率均值为4.15%,试验结果与理论优化结果一致。 (1)设计了一款适合丘陵山区小粒咖啡收获的手持振动梳刷式采摘装置。通过分析小粒咖啡果实-果柄力学模型,得到果实脱离果柄的条件;通过理论计算与动力学仿真,确定采摘机的结构参数和工作参数;通过对小粒咖啡果树-机械收获动力学模型进行分析,确定了简谐运动过程中振幅的稳态响应表达式,为采摘机的设计提供了理论基础。 (2)利用ADAMS建立果树-机械刚柔耦合模型进行仿真分析,确定最佳摩擦阻力为4.2 N;确定偏心块夹角在0°~90°之间变化时,平均振幅先减小后增大。对采摘机收获过程进行了单因素仿真试验,确定影响采摘机收获效果的主要因素为频率、梳齿间距和偏心块夹角,频率水平范围20~30 Hz、梳齿间距水平范围20~40 mm、偏心块夹角水平范围0°~45°。 (3)通过设计二次回归正交旋转组合试验,得到采净率、采青率和损伤率的回归方程,经方差分析可知,影响采净率和采青率的因素重要性依次为频率、梳齿间距和偏心块夹角,其中频率与梳齿间距的交互作用不容忽视,影响损伤率的因素重要性依次为梳齿间距、频率和偏心块夹角,其中频率与梳齿间距存在交互作用。通过参数优化和试验验证,当偏心块夹角为22.5°、频率为26 Hz、梳齿间距为32 mm时,采净率为91.35%,采青率为8.46%,损伤率为4.15%。2 果树-机械动力学模型建立与关键部件设计
2.1 果树-机械收获动力学模型建立
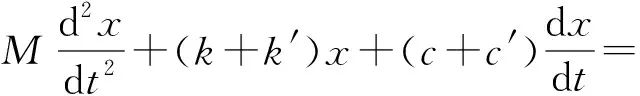
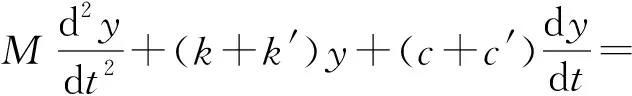
(c+c′)Axωcos(ωt-γx)=
2mω2rcosφ0cosγxsin(ωt-γx)+
2mω2rcosφ0sinγxcos(ωt-γx)
(c+c′)Ayωsin(ωt-γy)=
2mω2rsinφ0cosγxsin(ωt-γy)+
2mω2rsinφ0sinγxcos(ωt-γy)2.2 关键部件设计
3 仿真分析
3.1 果树-机械刚柔耦合模型建立


3.2 采摘机仿真分析

3.3 单因素仿真试验
4 收获性能试验
4.1 试验条件
4.2 试验方案

4.3 试验结果及方差分析



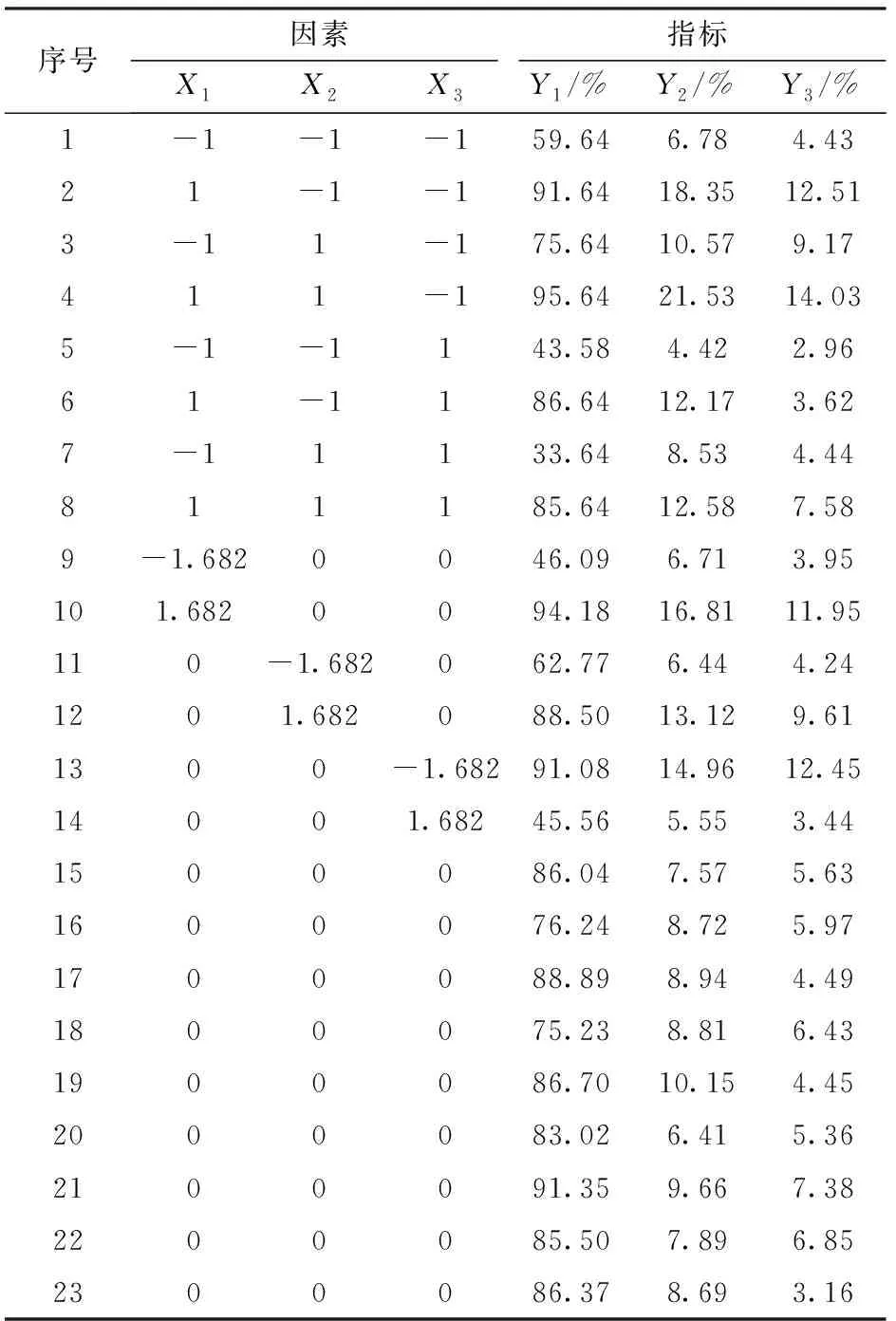
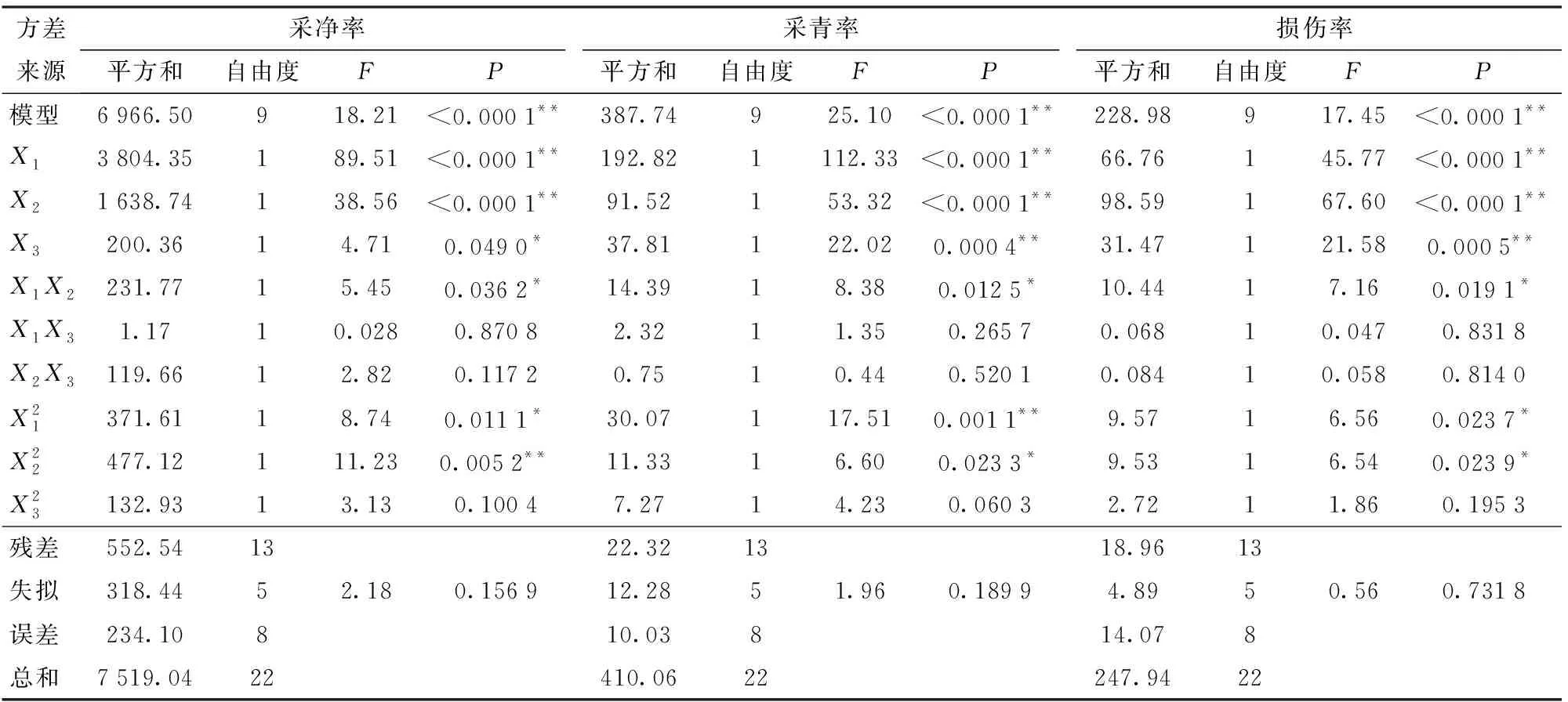
4.4 参数优化
5 结论
