以砂鱼蜥头部为原型的仿生深松铲尖设计与离散元仿真

张智泓 甘帅汇 左国标 佟 金

(1.昆明理工大学农业与食品学院， 昆明 650500; 2.吉林大学生物与农业工程学院， 长春 130022;3.吉林大学工程仿生教育部重点实验室， 长春 130022)

0 引言

深松作为一项重要的保护性耕作技术，可有效改善土壤压实问题，实现作物的增产增收，在世界范围内得到了广泛应用[1-2]。然而目前耕地作业的能量消耗大，占农业田间作业的40%～60%[3-4],随着耕深和耕速的增加，造成的深松工作阻力大、能量损失及作业效率低是深松领域迫切需要解决的问题[5]。目前，深松减阻方法主要包括电子渗透减阻、分层深松减阻、振动深松减阻和结构优化减阻等[6-7]，但分层和振动深松仍存在能量消耗大、机械结构复杂等问题。许多研究证明，在结构方面对深松铲进行优化设计，即通过改变破土刃口曲线及铲柄、铲尖的几何结构，可减小耕作阻力和能量损失[8]。

近年来，仿生学不断被有效应用于农机具的结构优化。田鼠、野猪及狗獾等土壤挖掘动物的几何特征被应用于深松铲的优化设计，且具有良好的减阻效果[9-11]。

砂鱼蜥是一种来自撒哈拉沙漠地带的特殊土壤动物，形态学和行为学的结合使其有效适应了沙漠环境，可在沙土内部实现快速运动。BAUMGARTNER[12]在砂鱼蜥鳞片表面发现特殊的微刺结构，使其具有较好的耐磨性，保护其体表在运动过程中不受砂砾损伤。MALADEN等[13]发现砂鱼蜥主要由身体和尾巴提供大振幅正弦波摆动力，再通过其头部瞬间破土，然后钻进沙丘内部运动。作为前进过程中直接破土的部位，砂鱼蜥头部的特殊几何特征是其具有优异破土减阻性能从而在土壤内部迅速运动的重要因素。

土壤耕作部件结构直接影响农机具的性能[14]，而铲尖作为深松铲的关键部件，其结构形状对深松铲作业过程中所需牵引力及土壤扰动行为有很大的影响，从而影响深松的作业效率与能源消耗。因此可基于土壤动物头部，利用逆向工程技术对其几何特征进行提取，将提取的轮廓拟合曲线进行参数化建模并设计仿生深松铲铲尖，以实现由生物模型到数学模型的转化。

采用离散元法对触土部件工作性能进行评价和分析逐渐成为研究热点，是一种用于模拟并分析散体介质系统动力学行为的数值方法[15]。农机具耕作过程的模拟仿真是一项复杂的工作，而离散元法从微观的角度对仿真系统中的每个散体颗粒进行分析，能够很大程度上提高模拟准确性，使仿真结果更加接近于实际情况[16]。

本文基于仿生学原理，结合砂鱼蜥头部特殊的几何结构特征设计深松铲铲尖；通过土壤垂直贯入试验，获得力-位移曲线及贯入阻力；将模拟与实测结果进行对比，以验证离散元方法的有效性；利用离散元法模拟土壤颗粒分别与仿生深松铲和普通深松铲相互作用后的力学行为及颗粒运动情况，为深松作业的节能减阻提供理论基础和设计依据。

1 基于砂鱼蜥头部几何结构特征的仿生深松铲设计

1.1 砂鱼蜥头部三维点云提取和模型建立

本文选取的仿生原型为成年砂鱼蜥(Scincusscincus)，体长18 cm，头部长2 cm，宽2 cm，如图1所示。

通过逆向工程对砂鱼蜥的头部结构进行提取。为获得清晰的砂鱼蜥头部特征曲面，用清水洗去砂鱼蜥体表杂物，然后用无水乙醇消毒，并用蒸馏水清洗干净，待干燥后在砂鱼蜥身体表面均匀喷涂DPT-5型显像剂(图2a)，为了获得完整头部三维点云模型，将砂鱼蜥身体用支架抬高并固定于自动转台，使用桌面级高精度物体白光3D扫描仪(Wiiboox Reeyee系列，南京威布三维科技有限公司)对砂鱼蜥身体进行360°扫描，获取砂鱼蜥原始三维点云模型。将扫描得到的原始点云模型文件导入到逆向工程软件Geomagic Wrap中，对点云模型进行删除噪声点、平滑等一系列修复过程后获得精确曲面(图2b)。

1.2 砂鱼蜥头部特征曲线量化分析

为获得砂鱼蜥头部特殊曲面，分别提取其俯视及侧视的轮廓线。如图3所示，将经过处理的砂鱼蜥头部曲面点云导入点云处理软件Imageware，沿各坐标轴对齐，提取点云曲线[17]，设置等距离的5个截面，并获得5条二维点云曲线(图中从左到右依次为y1、y2、y3、y4和y5)。

将提取的点云曲线导入AutoCAD软件获得具体的坐标数据，利用Matlab对点云数据进行多项式拟合。5条头部侧视特征曲线如图4a所示，侧视拟合曲线方程分别为

y1=3.635×10-5x6+1.131×10-3x5+1.282×10-2x4+
6.531×10-2x3+0.202 2x2+0.196 8x+3.94×10-2
(R2=0.999 6)

(1)

y2=5.189×10-6x6+2.173×10-4x5+3.392×10-3x4+
2.583×10-2x3+0.140 6x2+0.186x+6.132×10-2
(R2=0.999 3)

(2)

y3=5.452×10-6x6+2.694×10-4x5+5.116×10-3x4+
4.703×10-2x3+0.236 4x2+0.225 7x+4.583×10-2
(R2=0.999 3)

(3)

y4=4.701×10-6x6+2.242×10-4x5+4.103×10-3x4+
3.623×10-2x3+0.177 2x2+2.991×10-2x+
5.049×10-2(R2=0.999 8)

(4)

y5=6.105×10-5x6+1.91×10-3x5+2.168×10-2x4+
0.107 2x3+0.236 6x2-0.193 1x+1.876×10-2
(R2=0.999 8)

(5)

头部俯视特征轮廓曲线作为砂鱼蜥头部最先接触土壤并破土的重要部位，通过图像处理获得其拟合曲线[18]，如图4b所示。俯视拟合曲线方程式为

y6=1.532 18×10-7x4-1.097 67×10-4x3+
1.237×10-2x2+2.960 32x-45.313 61
(R2=0.991 9)

(6)

5条侧视和1条俯视特征曲线拟合曲线方程的R2均大于0.99，保障了拟合精度。

1.3 仿生铲尖设计与建模

结合上述拟合曲线相关参数，通过CATIA软件中创成式外形设计进行曲面重构，将铲尖的触土面设计为拟合曲面，以凿型铲尖T-S为对比，以俯视曲线为水平面轮廓线，分别以y3曲线为脊线，以y1、y3、y5曲线为脊线，及以y1～y5共5条曲线为脊线，建立仿生铲尖模型，一共设计3种仿生铲尖，分别为B-S-1、B-S-2、B-S-3，宽度为60 mm，长度为165 mm，如图5所示。

2 深松铲作业过程离散元仿真

2.1 接触模型选择

采用MORRISSEY[19]提出的包含非线性弹塑性变形与粘结力的接触模型，即EEPA模型，用于模拟深松铲作业时土壤产生的弹塑性变形以及土壤之间由于水分的存在产生的粘结力。颗粒与深松铲之间的接触模型则采用EDEM中默认的Hertz-Mindlin (no-slip)模型。

确定EEPA模型在EDEM中的应用参数[20]，包括初始接触力f0、细观接触表面能Δγ、接触塑形比λp、非线性曲线幂指数n、粘附分支曲线幂指数x和切向刚度因子ξm。各参数分别为：f0=0 N，Δγ=50 J/m2，λp=0.7，n=1.5，x=5，ξm=0.285 71。

2.2 深松铲与土壤相互作用离散元模型建立

深松铲主要由圆弧形铲柄和铲尖组成，圆弧形铲柄高度760 mm，宽度60 mm，曲率半径300 mm，入土角为23°(即铲尖安装角度)。深松铲铲尖的宽度为60 mm，长165 mm，将4组铲尖安装于深松铲铲柄，完成深松铲的设计建模，图6a为装配有T-S凿型铲尖的深松铲。图6b为3种仿生铲尖与铲柄进行配合并组装成的仿生深松铲。然后通过离散元对仿生铲尖在实际土壤中的耕作效果和阻力情况进行仿真分析。

为使离散元法分析土壤深松更符合田间实际作业情况以达到更高的准确性，目前离散元用于深松铲的研究逐渐由单层土层转变成综合考虑实际条件下的田间土壤分层情况，实际地表土壤由上到下0～170 mm为耕作层、170～300 mm为犁底层和300～500 mm为心土层[21]。耕作层中常年进行秸秆粉碎、旋耕作业，土壤容重较小；而长期受到表土作业机械的打击、挤压和降水时粘粒随水沉淀后形成犁底层，土壤透气、透水性差，质地较为紧实；心土层保持开垦种植前自然土壤淀积层的形态和性状。对3层土壤颗粒参数分别进行测定，获得各层土壤的剪切模量[22]，离散元仿真参数如表1所示[22-23]。

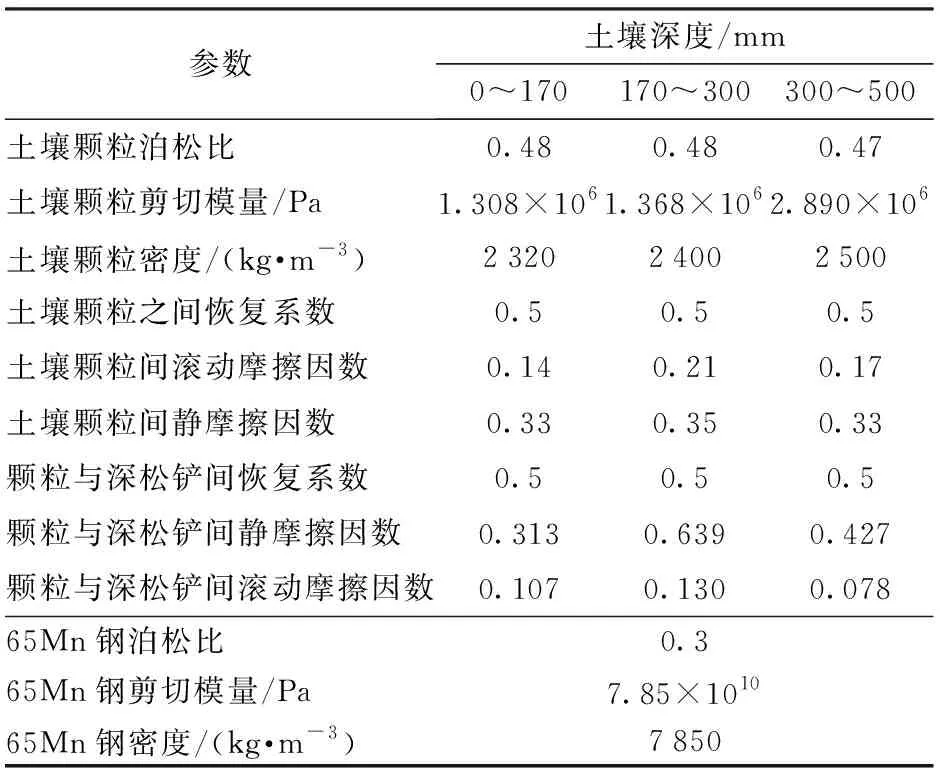
表1 离散元法仿真的基本参数Tab.1 Basic parameters of discrete element method simulation

如图7所示，采用长2 000 mm、宽600 mm、高500 mm的模拟土槽，土槽耕作层随机生成颗粒1 240 830个；犁底层随机生成颗粒1 029 450个；心土层随机生成颗粒1 338 870个。待所有颗粒沉降稳定后土槽建立完成，将深松铲导入到EDEM中进行仿真，求解的阻力包括深松铲运动过程中沿水平方向所需的牵引力和沿竖直方向所受的垂直力。

2.3 离散元仿真结果与分析

2.3.1深松铲作业所需牵引力求解

在深松铲进入土槽后，铲尖对犁底层土壤进行剪切和挤压，形成连续裂缝，断裂以弹性变形的形式开始，在铲柄切土刃的剪切作用、直铲柄段的挤压作用下进一步破裂、松碎，土壤颗粒沿垂直于铲尖及铲柄圆弧段方向向上及两侧抬升，对深松铲产生反作用力(所需牵引力和所受垂直力)，接着进入非弹性阶段直至变形极限，即阻力趋于稳定[24]。而深松铲后方的土壤则在重力的作用下，随着深松铲的前进而下落，回填垄沟。仿真中所需牵引力和垂直力随时间的变化趋势如图8所示，图中稳定波动阶段为0.5～1.8 s，不同的作业速度下稳定波动阶段时间不同。在作业速度为1 m/s，耕深为300、350、400 mm，以及耕深在300 mm，速度为0.8、1.0、1.2 m/s的作业条件下，B-S-1、B-S-2、B-S-3与T-S进行对比仿真。采用稳定波动阶段的力平均值绝对值作为各组铲尖在土壤中所需的牵引力和所受的垂直力。牵引力和垂直力是农机具与土壤接触的两个重要参数，分别决定了工具的牵引功率需求和土壤渗透能力[10]。

如图9、10所示，在不同作业速度和深度条件下，仿生深松铲的牵引力和垂直力都小于普通深松铲T-S，其中，B-S-2在仿生深松铲中牵引力最小，相对于凿型铲尖，其减阻率为8.34%～19.31%；其次为B-S-3和B-S-1。例如，在耕深300 mm，作业速度1.2 m/s的作业条件下，T-S具有1 086.45 N的牵引力和505.11 N的垂直力，B-S-1、B-S-2和B-S-3的牵引力分别为1 024.36、995.82、1 000.47 N，垂直力分别为442.31、414.55、423.48 N。仿生深松铲B-S-2具有更低的所需牵引力，也意味着更少的能量功率消耗[21]。深松铲受力以水平方向牵引力为主，垂直方向受力小于水平牵引力；而垂直力越大，铲面受到向下的挤压力更大，所需牵引力也随之增大。此外，深松铲的牵引力取决于土壤颗粒的加速力和铲面上的土壤重力[25]；而土壤颗粒的加速力又取决于工作部件的速度以及耕作深度。随着前进速度和耕作深度的增加，牵引力和垂直力也明显增大。可以推测当耕作深度和作业速度越大，扰动的土壤颗粒数量增加，产生较大的土壤扰动，从而具有较大的牵引力与垂直力。

2.3.2铲型几何特征对耕作阻力的影响

竖直方向外缘轮廓侧视仿生曲线(y1～y5)的曲率如图11a所示，该曲率变化规律与东方蝼蛄、鼹鼠前足和熊的爪趾外轮廓较为类似[26-27]，在靠近铲尖前端处曲率较大，越中间曲率变化较为平稳，其曲率变化有利于碎土，产生的碎土沿铲边流过，降低土壤对铲尖的垂直方向受力，从而减小水平方向所需牵引力。仿生深松铲的减阻效果归因于仿生铲尖的曲面结构，如图11b所示，水平面外缘轮廓俯视仿生曲线(y6)具有明显的曲率变化，中间段有较大峰值，两侧接近于0，该变化规律与蝼蛄背板及野猪头部的吻突部位较为类似[11,27]，该几何特征可将土壤的挤压载荷分散到铲尖尖端两侧，起到应力分散的作用，从而降低土壤对铲尖的耕作阻力。

实施翻转课堂教学模式，活跃了课堂气氛，加强了学生的参与度，带来了课堂的高效性；大幅度增加了课上课下的互动时间，带来了师生和生生的深度互动性；激发了学生的学习兴趣，带来了学生学习的主动性；学生可自定学习步调，实现了学生学习的个性化；有充裕的时间培养合作学习、探究学习等，提高了学生协作沟通、创新等能力的培养；网络教学平台记录了所有学生学习的全部信息，实现了课程考核的过程化。

由于3种铲尖的仿生曲线组合形式不同，与之对应仿生铲尖曲面的复杂程度也不同。考虑到仿生铲尖B-S-1仅包含特征曲线y3，其仿生曲面与其它仿生铲尖相比较为简单，然而，仅由特征曲线y3构成的仿生铲尖曲面没有明显减小其表面与土壤颗粒的挤压力，相对于凿型铲尖，B-S-1的减阻效果主要归因于俯视仿生曲线y6；由3条特征曲线组合而成的仿生铲尖B-S-2的表面相对更为光滑，B-S-2在土壤内部前进时对土体的破坏使土壤颗粒具有较好的流动性[8]。而对于B-S-3，特征曲线y1和y3以及y3和y5之间存在有明显凹棱，对照砂鱼蜥头部结构特征，发现砂鱼蜥鼻孔位于该凹棱处，从砂鱼蜥生理学角度分析，该凹棱结构有助于砂鱼蜥在土壤内部运动过程中进行呼吸，然而，从减阻效果而言，凹棱影响了土壤的流动行为[28]，从而削弱了仿生曲面的减阻效果。

2.3.3土壤颗粒速度场分析

在耕深300 mm、作业速度0.8 m/s的稳定阶段，将被扰动的土壤颗粒的速度场用矢量的形式表示[29]，图12为4种深松铲扰动下的土壤速度矢量图，每个颗粒的速度用箭头表示，箭头长度和方向分别表示速度大小和方向。土壤颗粒在深松铲尖作用下开始运动达到稳定阶段后，由箭头大小和颜色可以看出，在T-S铲尖的中后段土壤颗粒速度较大、尖端土壤颗粒速度较小，而仿生铲尖的尖端表面的土壤颗粒速度较大，也正是在入土初期仿生铲尖阻力的增长速度大于T-S的原因[22]，但是这更有利于仿生铲尖在前进时打破犁底层。由箭头方向可以看出，在所有铲尖中上段，土壤颗粒朝着圆弧形铲柄的圆心方向运动，但是在T-S铲尖中后段具有速度的土壤颗粒数量大于仿生铲尖，虽然对土壤有着更大的提升效果，但是更容易造成土壤颗粒向上堆积，不断挤压深松铲，阻碍前进且增大垂直力。如图13所示，在T-S铲尖前端，土壤颗粒分布均匀，运动方向基本一致，而在仿生铲尖前端，由于仿生铲尖在前进方向上与颗粒接触面积较少，且主要集中于铲尖前端，土壤颗粒运动方向沿着仿生曲面发生变化，仿生铲尖改变了土壤颗粒的流动方向，增加了流动性，分散了颗粒的堆积效应，从而减少了牵引力和垂直力。

2.3.4土壤扰动行为求解与分析

土壤扰动被定义为耕作部件作业时产生的土壤松动、运动和混合。底土耕作通常是为了改善压实土壤的透气性和透水性，从而改善作物根系生长环境[22]。铲尖作为破土主要部件，其形状对土壤扰动也有一定的影响[26]，在铲尖附近的土壤会受到更多的扰动，扰动区域面积是评价耕作质量的重要指标。在实际深松过程中，深松铲对土壤的过度扰动会增加土壤水分的蒸发量，不利于土壤保墒，因此既要保证深松铲对土壤的疏松，又要减少土壤的扰动，并且打破犁底层[24]。

离散元模型中虚拟土槽的纵向截面图和横向截面图如图14所示，截取犁底层附近的土壤颗粒，图中颜色代表颗粒的瞬时速度。在耕深300 mm、作业速度0.8 m/s的作业条件下，4种深松铲所形成的扰动情况相似，各层的土壤颗粒均因为扰动产生了速度和位移。

为了精确地比较不同深松铲作业时对土壤的扰动情况，在EDEM中求解体积内颗粒的总动能。通过后处理，设置长、宽、高分别为300、600、130 mm的监测器(图7)，放置于虚拟土槽模型犁底层的中间位置(图14白色虚线内)。

离散元模型求解得到的体积内颗粒的总动能如图15a所示，深松铲在经过监测器[30]时，监测器内颗粒总动能不断增加，随着深松铲前进不断减小。如图15b所示，在同一时间段内，测得颗粒总动能最大为T-S(0.538 56 J)，最小为B-S-2(0.365 57 J)，其次是B-S-3(0.385 46 J)、B-S-1(0.463 42 J)。颗粒的动能主要由深松铲的动能转化而来，说明仿生铲尖在前进过程中打破犁底层时所消耗的能量小于凿型铲尖。

3 深松铲减阻性能试验

3.1 深松铲制备及土槽试验平台搭建

为了通过实践检验仿生铲尖设计的合理性，在昆明理工大学土槽实验室内进行试验。试验土壤选用云南省耕作用的红壤土，测得不同深度下土壤含水率和土壤密度平均值，如表2所示。

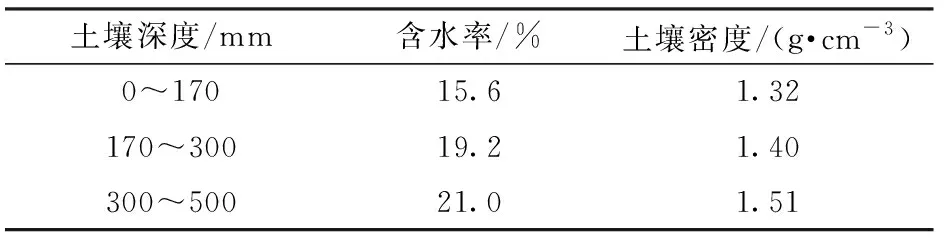
表2 不同深度土壤含水率和密度Tab.2 Soil moisture content and density at different depths

采用金属3D打印技术制备仿生铲尖和凿型铲尖，材质均为铝合金。试验用深松铲如图16所示。

试验时将土槽分为加速区、测试区和减速区3部分，其中测试区为3 m，加速和减速区各0.5 mm。分别在作业速度为1.0 m/s，耕作深度为300、350、400 mm，以及耕作深度为300 mm时，作业速度为0.8、1.0、1.2 m/s条件下进行土槽试验，试验指标为深松铲作业时所需牵引力，将深松铲在前进方向所需牵引力与相同试验条件下的离散元模拟结果进行对比。

试验装置由试验台车、深松铲连接装置和阻力测试系统等组成，如图17所示。试验主要仪器设备有(图17a)：S型JLBS-1拉压传感器(蚌埠金诺传感器有限公司)、XMT-808-I型数据显示器(蚌埠金诺传感器有限公司)。深松铲与试验台车通过S型JLBS-1拉压传感器相连接(图17b)，在前进过程中土壤对深松铲产生的水平方向所需牵引力转化为对传感器的拉力，再转变为电信号在XMT-808-I型数据显示器上实时显示，最后通过牵引力测试系统保存试验数据，采样频率为10 Hz。

3.2 土槽试验与仿真结果对比

在3种作业速度、3种耕作深度下所需牵引力的仿真与试验结果对比如表3所示。在前进速度一定时，深松铲的牵引力会随着耕作深度的增大而增大，仿生铲尖相对于国标凿型铲尖具有减阻效果，减阻率为5.74%～9.64%。深松铲的牵引力在耕作深度一定时也会随着前进速度的增大而增大，仿生铲尖的减阻率为5.34%～8.85%。在仿生深松铲中，B-S-2的减阻效果最好，其次是B-S-3和B-S-1，减阻效果与EDEM仿真结果一致，仿真与土槽试验的误差范围在10.83%～17.06%之间。

表3 不同作业速度和耕作深度下所需牵引力试验结果Tab.3 Experiment results of draft force with different speeds and depths

3.3 铲尖垂直贯入土壤阻力实测结果及其与仿真相关性分析

3.3.1垂直贯入土壤实测试验与仿真分析方法

为了更为细致地分析仿生铲尖减阻机理，同时进一步检验本研究所采用的离散元法仿真模型的准确性，开展不同铲尖土壤垂直贯入实测试验与仿真。如图18a所示，在仿生设计的基础上，将模型调整为便于贯入试验的试样形式，宽度20 mm，长度70 mm。通过快速成型加工技术将4个试件导入Wiiboox Mini系列3D打印机(南京威布三维科技有限公司)进行制备，打印材料采用生物降解塑料聚乳酸(PLA)，打印精度0.1 mm，其弹性模量为3×104MPa，弯曲模量为100～150 MPa，密度为1.26×103kg/m3，拉伸强度为40～60 MPa，加工温度170～230℃，制备的试样如图18b所示。

由于铲尖主要功能为打破犁底层，因此实测试验所使用的土壤收集于耕作田地犁底层，将收集的土壤干燥后，挑拣出杂物，用筛孔半径为3 mm的筛子筛分土壤颗粒，然后加入蒸馏水调节土壤含水率，测得土壤含水率为17.5%～18.5%，将试验用土壤填充入200 mm×200 mm×200 mm的铁质土槽中，由于箱体的直径远远大于仿生结构的直径，边界效应可以忽略不计[8]。为保证每次试验土壤条件一致，每次贯入试验后，疏松土壤，并用50 N的压土板进行压实。如图19a所示，使用P300系列电子万能试验机(济南美特斯测试技术有限公司)测量土壤贯入阻力，样件向下运动速度为4 mm/s，运动行程为60 mm，确保试样完全入土。试验因素为铲尖试样类型，试验指标为每个试样在垂直入土时所受的贯入阻力测量值，每个试样重复5次试验。垂直贯入土壤仿真同样使用犁底层土壤颗粒参数，仿真中采用与实测试验尺寸相同的土槽模型，土槽设置约束x和y两个方向的边界条件，在箱体的顶面即z方向上不受任何约束。设置颗粒半径为3 mm，随机生成颗粒31 772个，待所有颗粒沉降稳定后土槽建立完成。为确保仿真的精确度和求解效率，将参与计算的三维模型导入Workbench中，铲尖试样采用四面体网格进行划分，网格大小设置1 mm；土壤颗粒的网格尺寸按照仿真模拟中最小颗粒的半径度量，设置为颗粒半径的2.5倍，即7.5 mm。然后，将得到的各模型网格以.msh格式导入到EDEM中。设置以4 mm/s的恒定速度垂直入土，进入深度为60 mm，对几种不同铲尖模型进行仿真。离散元仿真模型结构参数与实测试验一致(图19b)。

3.3.2实测与仿真结果相关分析与误差比较

实测试验得到的4组贯入阻力-深度曲线如图20a所示。从图中可见，在入土深度小于40 mm时，仿生试样的贯入阻力及其增加的速度都大于普通试样T-S，然而，在贯入40 mm后直至试样完全进入土壤，贯入阻力增长速度小于普通试样T-S，T-S的贯入阻力最大，其次是B-S-1和B-S-3，最小的是B-S-2。

仿真得到的4组贯入阻力-深度曲线如图20b所示。由于仿真中颗粒离散程度较大，仿真求解得到的力随时间变化曲线有一定波动，仿生试样在入土深度小于30 mm时贯入阻力及其增加的速度都大于普通试样T-S，但是在30 mm后直至试样完全进入土壤，贯入阻力增长速度小于普通试样T-S。将不同铲尖离散元仿真求解得出的力随位移变化曲线与实测试验得到的曲线进行对比，对两组数据进行相关性分析，得到皮尔逊相关系数分别为0.994 2、0.993 1、0.989 9、0.988 6，表明实测结果与仿真结果吻合较好。

仿真得到的贯入阻力-深度曲线总体上与实测试验相近，但是由于仿真曲线的波动性，因此对仿真曲线进行拟合分析。

y=abx+c

(7)

拟合结果表明，各方程的拟合度R2均大于0.98，符合精度要求，各条拟合曲线方程为

yT-S=5.918 5×1.042 2x-3.809 1
(R2=0.989 4)

(8)

yB-S-1=6.812 6×1.038 8x-4.139 0
(R2=0.989 7)

(9)

yB-S-2=9.019 5×1.032 3x-6.230 7
(R2=0.983 8)

(10)

yB-S-3=11.267 7×1.028 9x-8.989 1
(R2=0.984 0)

(11)

在式(7)中，参数a、c决定初始阻力的大小，而参数b决定力的增长率[8]。由于B-S-1、B-S-2和B-S-3中的参数a、c均大于T-S，说明入土前期，仿生铲尖的贯入阻力大于凿型铲尖；而仿生铲尖B-S-1、B-S-2和B-S-3中的参数b均小于凿型铲尖T-S，说明贯入土壤至一定深度后，仿生试样的贯入阻力逐渐小于凿型铲尖，贯入土壤过程中，仿生铲尖特殊几何结构可以减缓贯入阻力的增长速度。

此外，比较不同铲尖试样在贯入土壤过程中产生的最大贯入阻力(表4)，仿真和实测试验结果均表明，T-S铲尖的贯入阻力最大，其次为B-S-1和B-S-3，减阻率最高的铲尖为B-S-2。由仿真结果计算得到，B-S-1、B-S-2和B-S-3的减阻率分别为9.64%、18.12%和16.30%；实测试验结果计算得到，B-S-1、B-S-2和B-S-3的减阻率分别为10.19%、18.12%和17.37%。仿真与实测的最大贯入阻力的相对误差为2.47%～3.91%，表明离散元仿真模型对不同铲尖贯入土壤时产生的最大贯入阻力具有较好的预测效果。

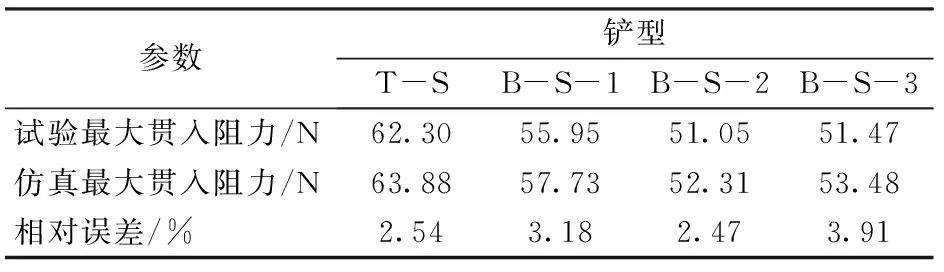
表4 不同铲尖试样最大贯入阻力试验结果与仿真结果Tab.4 Max force of different specimens in experiments and simulations

4 结论

(1)在EDEM中模拟实际土壤分层情况，将4组深松铲进行仿真对比试验，由于仿生曲线特殊的曲率特征，仿生铲尖B-S-2起到了较好的减阻效果，相对于凿型铲尖，其减阻率为8.34%～19.31%；并且随着耕作深度和作业速度的增加，所需牵引力与垂直力也增大。

(2)在入土初期，仿生铲尖表面土壤颗粒速度大于凿型铲尖T-S，仿生铲尖在前进时更容易打破犁底层。4组深松铲所形成的扰动情况相似，而在铲尖T-S上方的土壤颗粒扰动范围最大，B-S-2的扰动范围最小。仿生铲尖改变了土壤颗粒的流动方向，也减少了对土壤的扰动。

(3)土槽试验与仿真结果表明，B-S-2的减阻效果均最好，其次是B-S-3和B-S-1。仿真与试验的误差为10.83%～17.06%，由此验证离散元法对所需牵引力仿真的可行性，同时通过实践检验了仿生铲尖设计的合理性。

(4)贯入土壤阻力实测与仿真结果表明，实测与仿真中各组力-位移曲线趋势一致，与T-S进行比较，B-S-2贯入阻力均为最小，其次是B-S-3和B-S-1；仿生铲尖特殊几何结构可以减缓贯入阻力的增长速度，进一步探索了仿生铲尖的减阻机理；实测与仿真皮尔逊相关系数为0.994 2、0.993 1、0.989 9和0.988 6，最大贯入阻力的相对误差为2.47%～3.91%，表明离散元法对实际试验有着较好的预测效果。